FOCUS OF ATTENTION AND REGION SEGREGATION BY

LOW-LEVEL GEOMETRY

J. A. Martins, J. Rodrigues and J. M. H. du Buf

Vision Laboratory, Institute for Systems and Robotics (ISR), University of the Algarve, Campus de Gambelas, 8005-139 Faro, Portugal

Keywords:

Saliency, Focus-of-Attention, Region segregation, Colour, Texture.

Abstract:

Research has shown that regions with conspicuous colours are very effective in attracting attention, and that

regions with different textures also play an important role. We present a biologically plausible model to obtain

a saliency map for Focus-of-Attention (FoA), based on colour and texture boundaries. By applying grouping

cells which are devoted to low-level geometry, boundary information can be completed such that segregated

regions are obtained. Furthermore, we show that low-level geometry, in addition to rendering ﬁlled regions,

provides important local cues like corners, bars and blobs for region categorisation. The integration of FoA,

region segregation and categorisation is important for developing fast gist vision, i.e., which types of objects

are about where in a scene.

1 INTRODUCTION

Attention of animals, also primates and humans, is

rapidly drawn towards conspicuous objects and re-

gions in the visual environment. The ability to iden-

tify such objects and regions in complex and cluttered

environments is key to survival, for locating possi-

ble prey, predators, mates or landmarks for naviga-

tion (Elazary and Itti, 2008). But attention is only one

aspect. We start to understand how our visual sys-

tem works: (1) very fast extraction of global scene

gist, (2) also fast local gist for important objects and

a rough spatial layout map, (3) in parallel with (2) the

construction of a saliency map for Focus-of-Attention

(FoA), and only then (4) sequential screening of con-

spicuous regions for precise object recognition, using

peaks and regions in the saliency map with inhibition-

of-return in order not to ﬁxate the same region twice,

but with two strategies for FoA: ﬁrst covert attention

(automatic, data-driven) possibly followed by overt

attention (consciously directed). In addition, our vi-

sual system is not analysing all information for con-

structing a complete and detailed map of our environ-

ment; it concentrates on essential information for the

task at hand and it relies on the physical environment

as external memory (Rensink, 2000).

In this paper we concentrate on three aspects: (1)

the construction of a saliency map for FoA on the ba-

sis of colour, which was shown to be very effective in

attracting attention (van de Weijer et al., 2006), also

texture (du Buf, 2007), (2) a ﬁrst region segregation

by employing low-level geometry in terms of blobs,

bars and corners, and (3) using low-level geometry

allows us to reduce signiﬁcantly the dimensionality

of texture features. We note that our approach is not

based on the cortical multi-scale keypoint represen-

tation as recently proposed by Rodrigues and du Buf

(2006), who built saliency maps which work verywell

for the detection of facial landmarks and for invari-

ant object recognition on homogeneous backgrounds

(Rodrigues and du Buf, 2007), but may lead to enor-

mous amounts of local peaks in natural scenes.

2 COLOUR CONSPICUITY

Colour information in a saliency map was ﬁrst used

by Niebur and Koch (1996). Their model was later ex-

tended by Itti and Koch (2001), who integrated more

features, for instance intensity, edge orientation and

motion. In our approach to create a saliency model

which also contains cues for region and object segre-

gation, we therefore start by using colour information,

as this provides the most important input for attention

(van de Weijer et al., 2006), in order to build a colour

conspicuity map which will later be combined with a

texture map. But before using colour features the in-

put images must be corrected because a same object

will look different when illuminated by different light

sources, i.e., the number, power and spectra of these.

267

A. Martins J., A. Rodrigues J. and M. H. du Buf J. (2009).

FOCUS OF ATTENTION AND REGION SEGREGATION BY LOW-LEVEL GEOMETRY.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 267-272

DOI: 10.5220/0001768502670272

 SciTePress

The processing consists of the following four

steps: (a) colour illuminant and geometry normalisa-

tion deals with correcting the image’s colours. Let

each pixel P

of image I(x,y) be deﬁned as (R

)

and (L

) in both RGB and Lab colour spaces,

with i = {1...N}, N being the total number of pixels in

the image. We ﬁrst process the input image I

using

the two transformations described by Finlayson et al.

(1998), as shown below, both in RGB colour space.

Their method applies iteratively steps A and B, until

colour convergence is achieved (4–5 iterations). Each

individual pixel is ﬁrst corrected in step A for illumi-

nant geometry independency (i.e., chromaticity), by



+ G

+ B

+ G

+ B

+ G

+ B



(1)

followed in step B by global illuminant colour inde-

pendency (i.e., grey-world normalisation),

N·R

∑

j=1

N·G

∑

j=1

N·B

∑

j=1

. (2)

After the process is completed, the resulting RGB

image is converted to Lab colour space and the a

and

components, where subscript cc stands for colour-

corrected, are combined in I

together with the un-

modiﬁed L

channel from the input image I

. The

main idea for using the Lab space is that it is an al-

most linear colour space, i.e., it is more useful for

determining the conspicuity of borders between re-

gions. The reason for using the L

component instead

of the L

one is that, as observed by Finlayson et al.

(1998), the simple and fast repetition of steps A and

B does a remarkably good job. In fact, it does the job

too well because all gray pixels (with values R=G=B

from 0 to 255) end up having R=G=B=127. In other

words, all information in gray image regions would

be lost. Summarising, the initial I

image in RGB

is normalised to I

and then converted to the colour

space L

Figure 1 shows four input images which will be

used below, called extinguisher, park, ﬁsh and moun-

tain, all of size 256 × 256 pixels with 8 bits for

each colour component R, G and B. Figure 2 shows

three results of colour correction applied to the ex-

tinguisher image, from top-left to top-right: original

image, modiﬁed image with a blue tint (R –12%, G

+4% and B +50%), and modiﬁed image with a warm

white balance. The three results are shown below

the input images. As can be seen, colour correction

yields very similar images despite the rather large dif-

ferences in the input images. Colour correction as

explained above simulates colour constancy as em-

ployed in our visual system (Hubel, 1995).

Figure 1: Input images, left to right and top to bottom: ex-

tinguisher, park, ﬁsh and mountain.

The second step (b) is to reduce colour inhomo-

geneities in the images by adaptive smoothing of the

colour regions, while maintaining or even improving

the boundariesbetween different regions. We propose

a new, nonlinear, adaptive 1D ﬁlter, here explained in

the horizontal direction but it can be rotated, which

consists of a centred DOG

1,2

(x) = N



exp



−x

2σ



− exp



−x

2σ



, (3)

which is split into F

(x < 0) and F

(x > 0), and an-

other centred Gaussian, which is not split,

(x) = N

· exp



−x

2σ



, (4)

taking σ

≫ σ

. N

and N

are normalisation con-

stants which make the integrals of all three functions

equal to one. The three functions can be seen as a

simulation of a group of three cells at the same po-

sition, but with different dendritic ﬁelds which are

indirectly connected to cone receptors in the colour-

opponent channels a and b of Lab, F

yielding the

excitatory response of a receptive ﬁeld of an on-

centre cell, and F

1,2

yielding excitatory responses of

two off-centre cells. From the three cell responses

1,2,3

we ﬁrst compute the contrast between the left

) and right (R

) responses; mathematically C =

|(R

− R

)/(R

+ R

)|. Then, based on the contrast

C and the minimum difference between the centre re-

sponse (R

) and the left and right responses, the out-

put R is determined by

R =



+ (1−C)R

if |R

− R

| < |R

− R

+ (1−C)R

otherwise.

(5)

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

268

Figure 2: Colour illuminant and geometry normalisation.

Top: input images; bottom: respective results; see text.

In words, if the contrast is low, as in an almost ho-

mogeneous region, the ﬁlter support is big, but if the

contrast is high, at the boundary between two regions,

the ﬁlter support is small. This adaptive ﬁltering is

applied to I

at each pixel position (x,y), ﬁrst hori-

zontally (R

) and then vertically (R

(x,y) = R

(x,y)]], (6)

where subscript ci stands for colour-improved. In our

experiments we obtained good results with σ

= 7 and

= 3), and adaptive ﬁltering in horizontal and verti-

cal directions was sufﬁcient to sharpen blurred bound-

aries even with oblique orientations. Furthermore, the

processing is very fast because the three ﬁlter func-

tions need only be computed once.

After colour correction and adaptive ﬁltering, the

third step (c) serves to detect boundaries. In fact,

for this purpose we could use the contrast function

C described above, but in order to accelerate process-

ing we apply a simple gradient operator, as shown in

Fig. 3a and b, which requires only two convolutions,

with mask sizes of 5× 2 and 2×5, of the components

of I

. These masks can be seen as dendritic ﬁelds of

two cells, the two results being subtracted by a third

cell which combines horizontal and vertical gradients:

(x,y) =

∑

left

(x,y) −

∑

right

(x,y)

∑

top

(x,y) −

∑

bottom

(x,y).

(7)

(x,y) is then thresholded using

(x,y) =



1 if

(x,y) > k

0 otherwise,

(8)

where subscript ed stands for edge-detected. This

yields a binary edge map by means of a cell layer

in which cells are either active (response 1) or in-

active (response 0). We apply a global threshold

Figure 3: Gradient operators in vertical (a) and horizontal

(b) orientations with summation areas of 2 × 5 pixels, and

k = max(I

(x,y)). Edge detection yields three dis-

tinct maps, one for each component of Lab colour

space, I

, I

and I

, which can be combined.

In the last step (d), colour conspicuity at colour

edges is calculated at each position in the edge map

where there is an active cell (I

L,a,b

(x,y) = 1). We

deﬁne conspicuity Ψ at position (x,y) as the max-

imum difference between the colours in I

at four

pairs of symmetric points at distance l from (x, y),

i.e., on horizontal, vertical and two diagonal lines.

Figure 3c shows a cluster of gating cells. If the gat-

ing cells are called G

, opposing pairs are (G

i+4

with i = {1,...,4}, for example (G

). Partial con-

spicuity is then calculated independently for each of

the colour components in Lab space, as deﬁned by

(9a), where ~x

denotes the position of G

relative to

position (x, y). The ﬁnal value is then calculated us-

ing the sum of all three colour components (9b).

L,a,b

(x,y) = max



L,a,b

(~x

) − I

L,a,b

(~x

i+4



, (9a)

Lab

(x,y) = Ψ

(x,y) + Ψ

(x,y). (9b)

Results of colour conspicuity are shown in Fig. 4 top,

for the park and mountain images, using l = 4.

3 TEXTURE BOUNDARIES

Colour conspicuity Ψ

Lab

includes the luminance com-

ponent L and therefore luminance gradients, both in

coloured image regions and in non-coloured or gray

ones, but the processing as applied up to here is too

local to capture texture as a region property. As dif-

ferent colours in surrounding or neighbouring regions

attract attention, so do different textures because tex-

ture conveys complexity and therefore importance of

regions to attend for screening.

Texture processing is in principle completely

equal to colour processing, with adaptive ﬁltering,

gradient detection and the attribution of conspicuity

to texture boundaries, but instead of using the three

Lab components only the L one is used and texture

features must be extracted from L(x,y). Since we are

developing biologically plausible methods, it makes

sense to apply Gabor wavelets as a model of corti-

cal simple cells. Although very sophisticated texture

FOCUS OF ATTENTION AND REGION SEGREGATION BY LOW-LEVEL GEOMETRY

269

models have been proposed on the basis of the Ga-

bor model (du Buf, 2007), we will only use the spec-

tral decomposition here because of speed. This frees

CPU time for applying a reasonable number of fre-

quency (scale) and orientation channels, which will

be 8× 8 = 64 in this paper. Since Gabor ﬁltering in-

volves ﬁlter kernels which are relatively small (high-

frequency textures because of viewing distance), all

ﬁltering can be done in the frequency domain (see e.g.

Rodrigues and du Buf (2004)) and requires one for-

ward FFT and 64 inverse FFTs, the latter parallelised

on multi-core CPUs or even graphics boards (GPUs).

In the spatial domain, Gabor ﬁlters consist of a

real cosine and an imaginary sine component, both

with a Gaussian envelope, which resemble receptive

ﬁelds of simple cells with even R

s,i

and odd symmetry

s,i

, with i the orientation and s the scale. Responses

of complex cells are modelled by taking the modulus

s,i

(x,y) = [{R

s,i

(x,y)}

+ {R

s,i

(x,y)}

]

Texture boundaries are obtained by applying three

processing steps to the responses of complex cells,

at each individual scale and orientation, after which

results are combined: (a) the responses C

s,i

(x,y) are

smoothed using the adaptive ﬁlter deﬁned by eqns (3)

to (5), obtaining

s,i

. The next step (b) consists of

horizontal and vertical gradient detection C

s,i

, apply-

ing cells with dendritic ﬁelds of size 2× 5 as shown

in Fig. 3a, b to C

s,i

(x,y). The ﬁnal step (c) consists of

summing the results at all scales and orientations

R(x,y) =

∑

s,i

(x,y), (10)

together with an inhibition of all responses below a

threshold (we apply 0.1max{R(x,y)}). Figure 4 (bot-

tom) shows the results in the case of park and moun-

tain. As can be seen, the information is more diffuse

and complements that of colour processing (top).

4 SALIENCY MAP

A saliency map is built on top of colour conspicuity

and texture boundary maps by using grouping cells

which code local geometry. There are two levels of

grouping cells. At the ﬁrst, lower level, there are sum-

mation cells with a dendritic ﬁeld size of n × m, with

the centres at a distance d; see Fig. 5a. In this paper

we use m = n = 5 and d = 5, such that the dendritic

ﬁelds of the cells do not overlap. These cells sum ac-

tivities in the colour or texture maps, hence boundary

conspicuity at individual pixel positions is reinforced

at this level, but also at the next level which deals with

local geometry. At the second level, there are many

grouping cells, each one devoted to one geometric

Figure 4: Colour boundary conspicuity (top) for images

park (left) and mountain (right). Bottom: texture bound-

aries.

Figure 5: Grouping cells for low-level geometry: (a) cluster

of cells with their dendritic ﬁelds (circles) on a 5 × 5 grid;

(b) to (h) show examples of spatial conﬁgurations.

conﬁguration on a 5× 5 grid, but not all axons of the

cells at the lower level are used. This allows a sim-

ple construction of spatial conﬁgurations, as shown in

Fig. 5b to h, with up to four rotations, i.e., horizontal,

vertical and two diagonal orientations. The solid and

open circles in Fig. 5b to h refer to the use of the re-

sponses of the underlying summation cells: in case of

a solid circle the sum S needs to be positive (S > 0),

in case of an open circle S = 0, and responses of all

other summation cells on the grid are not used (they

are “don’t care”). Cells at this level take the maximum

of the responses of the excitated grouping cells, but

only if the spatial conﬁguration of the non-excitated

grouping cells is correct. If the response R of con-

ﬁguration c is R

, and if we call the conﬁguration of

cells which must be excitated Ω

and that of the cells

which must not be excitated Ω

, with Ω

,Ω

∈ Ω,

the 5× 5 grid, and Ω

∧ Ω

= 0, then

= max

i∈Ω

⇐

∑

j∈Ω

= 0. (11)

The conﬁgurations shown in Fig. 5b to h concern, re-

spectively, a line (or an isolated contour), a bar (two

parallel contours of a bar), two types of blobs and

three types of corners. The d and e conﬁgurations are

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

270

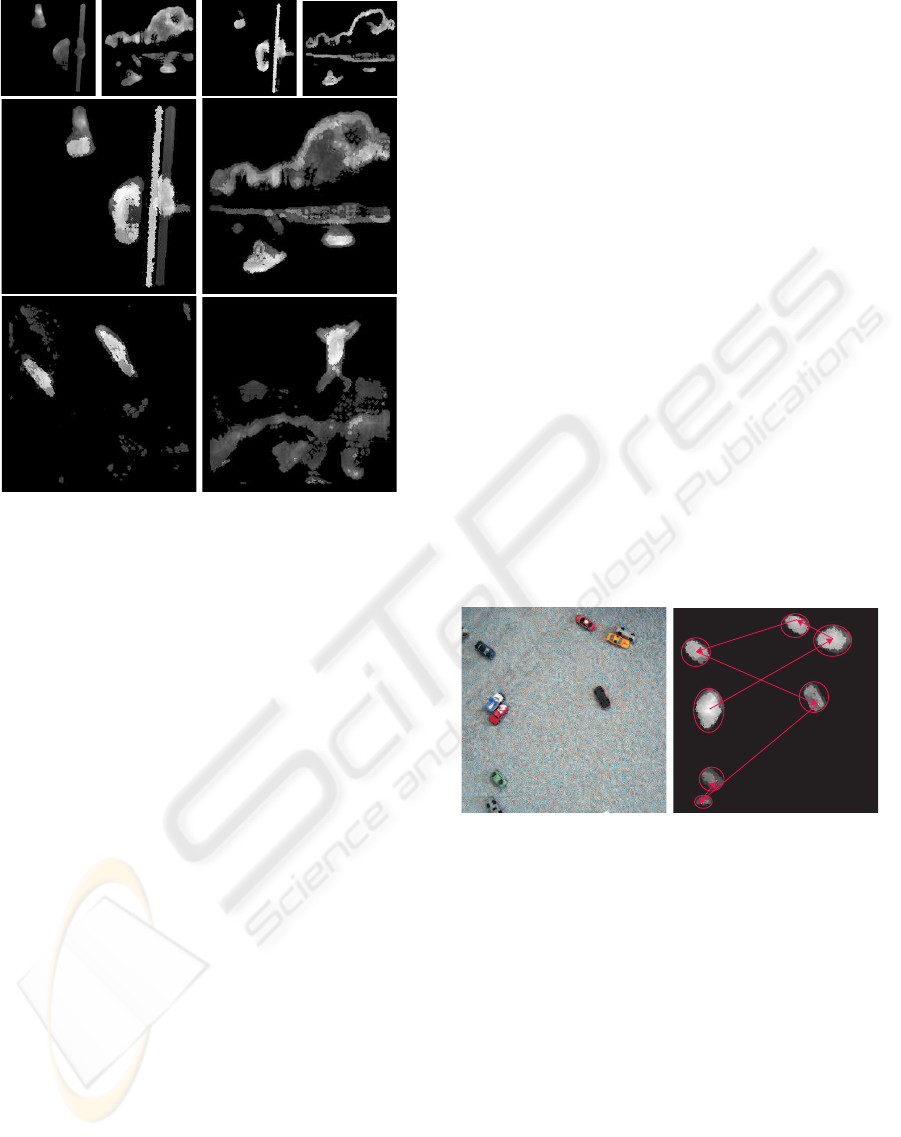
Figure 6: Saliency maps obtained by using only texture

boundaries (top-left), only colour conspicuity (top-right),

and by combining colour and texture (big images).

not rotated, but the other ﬁve are (horizontal, vertical

and two diagonal orientations), so in total there are 22

conﬁgurations c in the total set C. Since there may

be more conﬁgurations valid at the same position, the

last cell layer determines the response of the maxi-

mum conﬁguration, which yields the saliency map:

R(x,y) = max

c∈C

(x,y). (12)

The top row of Fig. 6 shows results obtained when

using only texture boundaries(at left), and those when

using only colour conspicuity (at right). As can be

seen, the maps are different but they complement each

other, i.e., texture in general yields more diffuse ar-

eas (park and mountain images) whereas colour con-

spicuity is more concentrated on contours. Combined

results, using texture and colour, of all four images

are shown in the lower part of Fig. 6. These ﬁnal

maps were created by taking the sum of the two val-

ues of the texture and colour saliency maps at each

pixel position. It should be stressed that all images

were normalised for visualisation purpose, darker ar-

eas corresponding to less saliency and brighter ones

to more saliency.

5 DISCUSSION

We introduced a simple, new, and biologically plau-

sible model for obtaining saliency maps based on

colour conspicuity and texture boundaries. The model

yields very good results in the case of natural scenes.

In contrast to the methods employed by Itti and Koch

(2001), whose saliency maps are very diffuse versions

of entire input images, our method is able to highlight

regions, a sort of pre-segregation of complex and con-

spicuous regions which is later required for precise

object segregation in combination with object cate-

gorisation and recognition.

The saliency maps provide crucial information

for sequential screening of image regions for object

recognition and tracking: FoA by ﬁxating conspicu-

ous regions, from the most important regions to the

least important ones. Figure 7 shows an input im-

age with toy cars (left), the saliency map (right), and

the order, indicated by arrows, in which the regions

will be processed. Fixation points were selected auto-

matically by determining the highest response in the

saliency map within each region, and regions are ﬁx-

ated using inhibition-of-return. Despite the fact that

saliency based on texture boundaries is more diffuse

than that on the basis of colour conspicuity, car-region

segregation is rather precise. The main reason for

this precision is that low-level geometry processing

mainly occurs at contours and inside objects, i.e., it

does not lead to region growing.

Figure 7: Toy cars image (left) and FoA-driven sequential

screening of regions (right).

The saliency model is now being extended by mo-

tion and disparity information, after which it can be

integrated into a complete architecture for invariant

object categorization and recognition (Rodrigues and

du Buf, 2006, 2007), which is based on multi-scale

keypoints, lines and edges derived from responses of

cortical simple, complex and end-stopped cells. This

is beyond the scope of this paper, but, as mentioned

in the Introduction, very fast global and local gist vi-

sion are two basic building blocks of an integrated

system. Until here, low-level geometry processing

has only been used for producing saliency maps for

FoA with segregated regions. But since low-level ge-

ometry information has already been extracted, it is

therefore available for obtaining local object gist, for

example providing cues which are used for a ﬁrst and

FOCUS OF ATTENTION AND REGION SEGREGATION BY LOW-LEVEL GEOMETRY

271

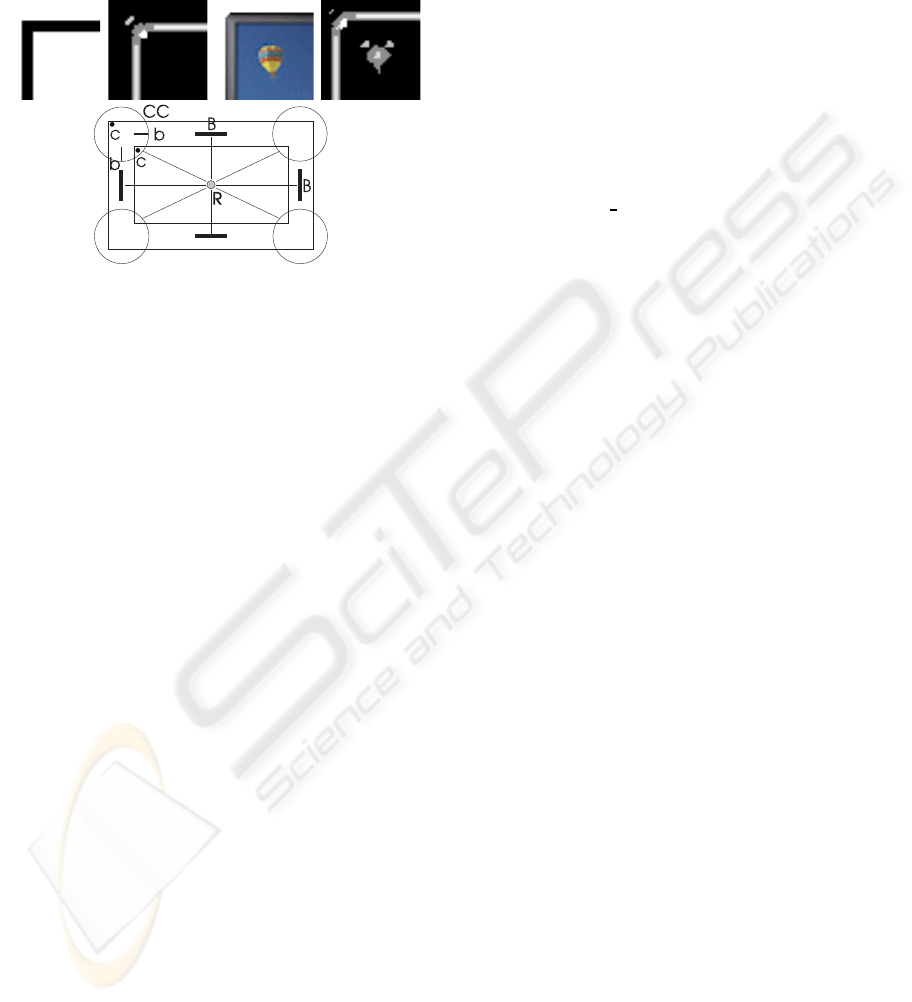
fast selection of possible object categories in memory

(Bar M., et al., 2006). This is a purely bottom-up and

data-parallel process for bootstrapping the serial ob-

ject categorization and recognition processes which

are controlled by top-down attention. Low-level ge-

Figure 8: Low-level geometry (top) and example of mid-

and high-level geometry groupings (bottom); see text for

details.

ometry is difﬁcult to visualise, because it consists of a

large number of spatial maps, in this paper limited to

22 but there could be more, one for each spatial con-

ﬁguration. Figure 8 (top), shows detail images with a

few conﬁgurations coded by different levels of gray,

i.e., corners, bars and blobs. The input was an ideal

rectangle with two sharp corners (left) and a com-

puter monitor with a sharp inner corner but rounded

outer one. Despite the outer corner being rounded,

evidence for a corner has been detected at two pixel

positions. These results were obtained on the basis of

colour conspicuity, but later texture and colour infor-

mation should be combined, and low-level geometry

should be used to construct mid- and high-levelgeom-

etry. The latter idea is illustrated in Fig. 8 (bottom):

at low level corners (c) and bars (b) are detected. At

mid level, these can be grouped into a complex corner

(CC), and at high level the CCs, together with linking

bars B, into a rectangle R. Such an R structure is typ-

ical for man-made objects, for example a computer

monitor or a photo frame. This example of high-level

geometry is perhaps the last level below semantic pro-

cessing: a computer monitor in combination with one

or more photo frames is an indication for global scene

gist: our ofﬁce. In any case, the large number of fea-

tures at the lowest level (64 Gabor channels) is re-

duced to the number of spatial conﬁgurations at low-

level geometry, here 22. Groupings at mid level (e.g.,

complex corner CC) may lead to less conﬁgurations,

but at high level (e.g., rectangle R) the number of con-

ﬁgurations will increase again, because many elemen-

tary shapes must be represented. On the other hand,

the precise localisation of conﬁgurations which is re-

quired at low level is not necessary at higher levels;

for example, grouping cells for complex corners CC

may be located somewhere near the centres of the cir-

cles in Fig. 8 (bottom), as long as their dendritic ﬁelds

are big enough to receive input from two corner and

two bar cells. These aspects are subject to further re-

search.

ACKNOWLEDGEMENTS

Research supported by the Portuguese Foundation for

Science and Technology (FCT), through the pluri-

annual funding of the Inst. for Systems and Robotics

through the POS Conhecimento Program (includes

FEDER funds), and by the FCT project SmartVision:

active vision for the blind (PTDC/EIA/73633/2006).

REFERENCES

Bar M., et al. (2006). Top-down facilitation of visual recog-

nition. PNAS, 103(2):449–454.

du Buf, J. (2007). Improved grating and bar cell models in

cortical area V1 and texture coding. Image and Vision

Computing, 25(6):873–882.

Elazary, L. and Itti, L. (2008). Interesting objects are visu-

ally salient. Journal of Vision, 8(3):1–15.

Finlayson, G., Schiele, B., and Crowley, J. (1998). Compre-

hensive colour image normalization. Proc. 5th Europ.

Conf. Comp. Vision, I:475–490.

Hubel, D. (1995). Eye, brain and vision. Scientiﬁc Ameri-

can Library.

Itti, L. and Koch, C. (2001). Computational modeling

of visual attention. Nature Reviews: Neuroscience,

2(3):194–203.

Niebur, E. and Koch, C. (1996). Control of selective vi-

sual attention: Modeling the ‘where’ pathway. Neural

Information Processing Systems, 8:802–808.

Rensink, R. (2000). The dynamic representation of scenes.

Visual Cogn., 7(1-3):17–42.

Rodrigues, J. and du Buf, J. (2004). Visual cortex fron-

tend: integrating lines, edges, keypoints and disparity.

Proc. Int. Conf. Image Anal. Recogn., Springer LNCS

3211(1):664–671.

Rodrigues, J. and du Buf, J. (2006). Multi-scale keypoints

in V1 and beyond: object segregation, scale selection,

saliency maps and face detection. BioSystems, 2:75–

90.

Rodrigues, J. and du Buf, J. (2007). Invariant multi-

scale object categorisation and recognition. Proc.

3rd Iberian Conf. on Patt. Recogn. and Image Anal.,

Springer LNCS 4477:459–466.

van de Weijer, J., Gevers, T., and Bagdanov, A. D. (2006).

Boosting color saliency in image feature detection.

IEEE Tr. PAMI, 28(1):150–156.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

272