
ACTIVE APPEARANCE MODEL FITTING UNDER OCCLUSION
USING FAST-ROBUST PCA
Markus Storer, Peter M. Roth, Martin Urschler, Horst Bischof
Institute for Computer Graphics and Vision, Graz University of Technology, Inffeldgasse 16/II, 8010 Graz, Austria
Josef A. Birchbauer
Siemens Biometrics Center, Siemens IT Solutions and Services, Strassgangerstrasse 315, 8054 Graz, Austria
Keywords:
Active appearance model, Fast robust PCA, AAM fitting under occlusion.
Abstract:
The Active Appearance Model (AAM) is a widely used method for model based vision showing excellent
results. But one major drawback is that the method is not robust against occlusions. Thus, if parts of the image
are occluded the method converges to local minima and the obtained results are unreliable. To overcome
this problem we propose a robust AAM fitting strategy. The main idea is to apply a robust PCA model to
reconstruct the missing feature information and to use the thus obtained image as input for the standard AAM
fitting process. Since existing methods for robust PCA reconstruction are computationally too expensive for
real-time processing we developed a more efficient method: fast robust PCA (FR-PCA). In fact, by using
our FR-PCA the computational effort is drastically reduced. Moreover, more accurate reconstructions are
obtained. In the experiments, we evaluated both, the fast robust PCA model on the publicly available ALOI
database and the whole robust AAM fitting chain on facial images. The results clearly show the benefits of our
approach in terms of accuracy and speed when processing disturbed data (i.e., images containing occlusions).
1 INTRODUCTION
Generative model-based approaches for feature local-
ization have received a lot of attention over the last
decade. Their key advantage is to use a priori knowl-
edge from a training stage for restricting the model
while searching for a model instance in an image.
Two specific instances of model-based approaches,
the Active Appearance Model (AAM) (Cootes et al.,
2001) and the closely related 3D Morphable Model
(3DMM) (Blanz and Vetter, 1999), have proven to
show excellent results in locating image features
in applications such as face detection and track-
ing (Matthews and Baker, 2004), face and facial ex-
pression recognition (Blanz and Vetter, 2003), or
medical image segmentation (Mitchell et al., 2001;
Beichel et al., 2005).
Despite its large success, the AAM model has one
main limitation. It is not robust against occlusions.
Thus, if important features are missing the AAM fit-
ting algorithm tends to get stuck in local minima.
This especially credits for human faces since the large
variability in the image data such as certain kinds of
glasses, makeups, or beards can not totally be cap-
tured in the training stage. Similar difficulties also
arise in other areas of model-based approaches (e.g.,
in the medical domain (Beichel et al., 2005)).
In the recent years some research was dedicated to
generative model-based approaches in the presence of
occlusions by investigating robust fitting strategies. In
the original AAM approach (Cootes et al., 2001) fit-
ting is treated as a least squares optimization prob-
lem, which is, of course, very sensitive to outliers due
to its quadratic error measure (L
2
norm). To over-
come this problem, the work of (Edwards et al., 1999)
extended the standard fitting method (a) by learning
the usual gray-value differences encountered during
training and (b) by ignoring gray-value differences
exceeding a threshold derived from these values dur-
ing fitting. But the main drawback of this method
is that the required threshold depends on the training
conditions, which makes it improper for real-life sit-
uations. In contrast, in (Dornaika and Ahlberg, 2002)
a RANSAC procedure is used for the initialization of
the AAM fitting in order to get rid of occlusions due
to differing poses. However, since the AAM fitting
130
Storer M., M. Roth P., Urschler M., Bischof H. and A. Birchbauer J. (2009).
ACTIVE APPEARANCE MODEL FITTING UNDER OCCLUSION USING FAST-ROBUST PCA.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 129-136
DOI: 10.5220/0001768701290136
Copyright
c
SciTePress

remains unchanged this approach has still problems
with appearance outliers.
Another direction of research was dedicated to re-
placing the least-squares error measure by a robust er-
ror measure in the fitting stage (Gross et al., 2006).
Later this approach was further refined by comparing
several robust error measures (Theobald et al., 2006).
The same strategy is also used in (Romdhani and Vet-
ter, 2003) and was adapted to a statistical framework
in (Yu et al., 2007). But the latter approach is lim-
ited in several ways: (a) a scale parameter is required,
which is hard to determine in general, (b) the frame-
work around the inverse compositional algorithm is
specifically tailored to tracking, and (c) the face mod-
els are built from the tracked person, which limits its
applicability for general applications.
In the context of medical image analysis a ro-
bust AAM fitting approach was presented in (Beichel
et al., 2005). In their method, which is based on the
standard AAM fitting algorithm, gross disturbances
(i.e., outliers) in the input image are avoided by ignor-
ing misleading coefficient updates in the fitting stage.
For that purpose, inlier and outlier coefficients are
identified by a Mean Shift based analysis of the resid-
ual’s modes. Then, an optimal sub-set of modes is se-
lected and only those pixels covered by the selected
mode combination are used for actual residual cal-
culation. The Robust AAM Matching (RAAM) ap-
proach shows excellent results on a number of medi-
cal data sets. However, the mode selection is compu-
tationally very complex. Thus, this method is imprac-
tical for real-time or near real-time applications.
To overcome these drawbacks we introduce a new
efficient robust AAM fitting scheme. In contrast
to existing methods the robustness (against occluded
features) is not directly included in the fitting step
but is detached. In fact, we propose to run a robust
pre-processing step first to generate undisturbed input
data and then to apply a standard AAM fitting. Since
the robust step, which is usually computationally in-
tensive, has to be performed only once (and not iter-
atively in the fitting process), the computational costs
can be reduced.
In particular, the main idea is to robustly replace
the missing feature information from a reliable model.
Thus, our work is somehow motivated by (Nguyen
et al., 2008) and (Du and Su, 2005), where beards
and eye-glasses, which are typical problems when ap-
plying an AAM approach, are removed. In (Du and
Su, 2005) a PCA model was built from facial images
that do not contain any eye-glasses. Then, in the re-
moval step the original input images are reconstructed
and the regions with the largest reconstruction errors
are identified. These pixels are iteratively replaced by
the reconstruction. But this approach can only be ap-
plied if the absolute number of missing pixels is quite
small. In contrast, in (Nguyen et al., 2008) two mod-
els are computed in parallel, one for bearded faces and
one for non-bearded faces. Then, in the removal step
for a bearded face the detected beard region is recon-
structed from the non-bearded space.
Since both methods are restricted to special types
of occlusion or limited by a pre-defined error level,
they can not be applied for general tasks. Thus, in
our approach we apply a robust PCA model (e.g.,
(Rao, 1997; Black and Jepson, 1996; Leonardis and
Bischof, 2000)) to cope with occlusions in the origi-
nal input data. For that purpose, in the learning stage
a reliable model is estimated from undisturbed data
(i.e., without any occlusions), which is then applied
to robustly reconstruct unreliable values from the dis-
turbed data. However, a drawback of these methods
is their computational complexity (i.e., iterative algo-
rithms, multiple hypothesis, etc.), which hinders prac-
tical applicability. Thus, as a second contribution, we
developed a more efficient robust PCA method that
overcomes this limitation.
Even though the proposed robust AAM fitting is
quite general, our main interest is to apply it to fa-
cial images. Thus, this application is evaluated in the
experiments in detail. However, we also note that it
is necessary that the image patch, where the robust
PCA is applied has to be roughly aligned with the
feature under consideration. In the case of our face
localization this can be ensured by using a rough face
and facial component detection algorithm inspired by
the Viola-Jones algorithm (Viola and Jones, 2004).
Moreover, the applied PCA model can handle a wide
variability in facial images.
This paper is structured as follows. In Section 2
we introduce and discuss the novel fast robust PCA
(FR-PCA) approach. In addition, we performed ex-
periments on the publicly available ALOI database,
which show that our approach outperforms existing
robust methods in terms of speed and accuracy. Next,
in Section 3, we introduce our robust AAM fitting al-
gorithm that is based on the new robust PCA scheme.
To demonstrate its benefits, we also present experi-
mental results on facial images. Finally, we discuss
our findings and conclude our work in Section 4.
2 FAST ROBUST PCA
If a PCA space U = [u
1
, . . . , u
n−1
] is estimated from n
samples, an unknown sample x = [x
1
, . . . , x
m
], m > n,
can usually be reconstructed to a sufficient degree of
accuracy by p, p < n, eigenvectors:
ACTIVE APPEARANCE MODEL FITTING UNDER OCCLUSION USING FAST-ROBUST PCA
131

˜
x = U
p
a +
¯
x =
p
∑
j=1
a
j
u
j
+
¯
x , (1)
where
¯
x is the sample mean and a = [a
1
, . . . , a
k
] are
the linear coefficients.
But if the sample x contains outliers (e.g., oc-
cluded pixels) Eq. (1) would not yield a reliable
reconstruction; a robust method is required (e.g.,
(Rao, 1997; Black and Jepson, 1996; Leonardis and
Bischof, 2000)). But since these methods are com-
putationally very expensive (i.e., they are based on
iterative algorithms) they are often not applicable in
practice. Thus, in the following we propose a more
efficient robust PCA approach.
2.1 Fast Robust Training
The training procedure, which is sub-divided into two
major parts, is illustrated in Figure 1. First, a standard
PCA subspace is generated from all training images.
Second, in addition, a large number of smaller sub-
spaces (sub-subspaces) is estimated from small sets of
randomly selected data points (sub-sampling). Since
occlusions are often considered to be spatially coher-
ent the sub-sampling is done in a smart way. Hence,
in addition to the random sampling over the whole im-
age region, the random sampling is also restricted to
image slices (vertical, horizontal, quadrant).
InputImages Subspace
x
PCA
.
.
.
.
x
x
x
x
.
x
.
.
x
x
x
x
x
3
...
.
.
x
x
x
1
2
.
x
.
.
.
.
.
.
RandomSampling
.
x
x
x
x
x
x
.
PCA
...
1
2
3
.
.
.
1
2
3
x
x
x
x
PCA
Sub‐Subspaces
...
Figure 1: FR-PCA training. Generation of the subspace
and the smaller sub-subspaces derived by randomly sub-
sampling the input images.
2.2 Fast Robust Reconstruction
Given a new unseen test sample x, the robust re-
construction is performed in two stages. In the first
stage (gross outlier detection), the outliers are de-
tected based on the sub-subspace reconstruction er-
rors. In the second stage (refinement), using the
thus estimated inliers a robust reconstruction
˜
x of the
whole image is generated.
Assuming that in the training stage N sub-
subspaces were estimated as described in Section 2.1,
first, in the gross outlier detection, N sub-samplings
s
n
are generated according to the corresponding sub-
subspace. In addition, we define the set of “in-
liers” r =
{
s
1
∪ . . . ∪ s
N
}
. This set of points is illus-
trated in Figure 2(a) (green points). Next, for each
sub-sampling s
n
a reconstruction
˜
s
n
is estimated by
Eq. (1), which allows to estimate the (pixel-wise)
error-maps
e
n
=
|
s
n
−
˜
s
n
|
, (2)
the mean reconstruction error ¯e over all sub-
samplings, and the mean reconstruction errors ¯e
n
for
each of the N sub-samplings.
Based on these errors we can detect the outliers by
local and global thresholding. For that purpose, the
sub-samplings s
n
are ranked by their mean error ¯e
n
.
The local thresholds (one for each sub-sampling) are
then defined by θ
n
= ¯e
n
w
n
, where the weight w
n
is es-
timated from the sub-sampling’s rank to remove less
outliers from first ranked sub-samplings. The global
threshold θ is set to the mean error ¯e. Then, all points
s
n,(i, j)
for which
e
n,(i, j)
> θ
n
or e
n,(i, j)
> θ (3)
are discarded from the sub-samplings s
n
obtaining
˜
s
n
.
Finally, we re-define the set of “inliers” by
r =
˜
s
1
∪ . . . ∪
˜
s
q
, (4)
where
˜
s
1
, . . . ,
˜
s
q
indicate the first ranked q sub-
samplings such that
|
r
|
≤ k and k is the pre-defined
maximum number of points. The thus obtained “in-
liers” are shown in Figure 2(b).
The gross outlier detection procedure allows to re-
move most outliers (i.e., occluded pixels), thus the
obtained set r contains almost only inliers. To fur-
ther improve the final result in the refinement step,
the final robust reconstruction is estimated similar to
(Leonardis and Bischof, 2000). In particular, start-
ing from the point set r = [r
1
, . . . , r
k
], k > p, obtained
from the gross outlier detection, an overdetermined
system of equations is iteratively solved, where the
following least square optimization problem
E(r) =
k
∑
i=1
(x
r
i
−
p
∑
j=1
a
j
u
j,r
i
)
2
(5)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
132

has to be solved obtaining the coefficients a. Hence,
the reconstruction
˜
x can be estimated and those points
with the largest reconstruction error are discarded
from r (selected by a reduction factor α). These steps
are iterated until a pre-defined number of remaining
pixels is reached. Thus, finally, an outlier-free sub-set
is obtained, which is illustrated in Figure 2(c), and the
robust reconstruction
˜
x can be estimated.
(a) (b) (c)
Figure 2: Data point selection process. (a) Data points sam-
pled by all sub-subspaces. (b) Remaining data points af-
ter applying the sub-subspace procedure. (c) Resulting data
points after the iterative refinement process for the calcula-
tion of the PCA coefficients.
Such a robust reconstruction result obtained by the
proposed approach compared to a non-robust method
is shown in Figure 3. One can clearly see that the
robust method considerably outperforms the standard
PCA. Note, that the blur visible in the reconstruction
of the FR-PCA is the consequence of taking into ac-
count only a limited number of eigenvectors.
(a) (b) (c)
Figure 3: Demonstration of the insensitivity of the robust
PCA to occlusions. (a) Occluded image, (b) reconstruction
using standard PCA, and (c) reconstruction using the FR-
PCA.
In general, the robust estimation of the coefficients
is computational very efficient and thus very fast. In
the gross outlier detection procedure only simple ma-
trix operations (standard PCA) have to be performed,
which are very fast; even if hundreds of sub-subspace
reconstructions have to be executed. The computa-
tionally more expensive part is the refinement step,
where an overdetermined linear system of equations
has to be solved iteratively. Since very few refinement
iterations have to be performed due to the preceding
gross outlier detection, the total runtime is kept small.
2.3 Experimental Results
To show the benefits of the proposed fast robust PCA
method (FR-PCA) we compared it to standard PCA
(PCA) and the robust PCA approach of (Leonardis
and Bischof, 2000) (R-PCA). We have chosen the lat-
ter one, because of its proven accuracy and applica-
bility. Our refinement process is similar to theirs.
Figure 4: Illustrative examples of objects used in the exper-
iments.
In particular, the experiments were evaluated on
the ”Amsterdam Library of Object Images (ALOI)”
database (Geusebroek et al., 2005). The ALOI
database consists of 1000 different objects. Over hun-
dred images of each object are recorded under differ-
ent viewing angles, illumination angles and illumina-
tion colors, yielding a total of 110,250 images. For
our experiments we arbitrarily chose 20 categories
(018, 032, 043, 074, 090, 093, 125, 127, 138, 151,
156, 174, 200, 299, 354, 368, 376, 809, 911, 926),
where an illustrative subset of objects is shown in Fig-
ure 4.
Table 1: Settings for the FR-PCA (a) and the R-PCA (b) for
the experiments.
Table 1: Settings for the FR-PCA (a) and the R-PCA (b) for the experiments.
(a)
FR‐PCA R‐PCA
Numberofinitialpointsk
130
p
NumberofinitialhypothesesH30
Reductionfactorα
0.9 Numberofinitialpointsk
48
p
Reductionfactorα 0.85
K
2
0.01
Compatibilitythreshold 100
(b)
FR‐PCA R‐PCA
Numberofinitialpointsk
130
p
NumberofinitialhypothesesH30
Reductionfactorα
0.9 Numberofinitialpointsk
48
p
Reductionfactorα 0.85
K
2
0.01
Compatibilitythreshold 100
Table 2: Comparison of the reconstruction errors of the standard PCA, the R-PCA and the FR-PCA. (a) RMS reconstruction-
error per pixel given by mean and standard deviation. (b) RMS reconstruction-error per pixel given by robust statistics:
median, upper- and lower quartile. Those results correspond to the box-plots in Figure 5.
(a)
Occlusion
mean std mean std mean std mean std mean std mean std
PCA 9.96 5.88 21.30 7.24 34.60 11.41 47.72 14.37 70.91 19.06 91.64 19.78
R‐PCA 11.32 6.92 11.39 7.03 11.98 8.02 20.40 19.90 59.73 32.54 87.83 26.07
FR‐PCA 10.99 6.42 11.50 6.69 11.59 6.71 11.66 6.88 26.48 23.57 73.20 27.79
70%
ErrorperPixel
0% 10% 20% 30% 50%
(b)
Occlusion
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
PCA 9.58 5.77 14.02 21.29 16.56 26.01 34.67 27.71 42.17 47.24 38.22 57.42 70.45 57.03 84.54 89.49 77.55 106.15
R‐PCA 10.54 6.39 15.81 10.63 6.50 15.76 10.95 6.60 16.16 13.83 7.96 23.13 62.76 32.47 82.98 87.80 70.64 104.99
FR‐PCA 10.46 6.57 15.15 10.97 6.96 15.88 11.01 7.01 16.06 10.98 7.08 16.10 17.25 9.75 36.33 75.04 56.84 92.61
ErrorperPixel
0% 10% 20% 30% 50% 70%
In our experimental setup, each object is repre-
sented in a separate subspace and a set of 1000 sub-
subspaces, where each sub-subspace contains 1% of
data points of the whole image. The variance retained
for the sub-subspaces is 95% and 98% for the whole
subspace, which is also used for the standard PCA and
the R-PCA. Unless otherwise noted, all experiments
are performed with the parameter settings given in Ta-
ACTIVE APPEARANCE MODEL FITTING UNDER OCCLUSION USING FAST-ROBUST PCA
133
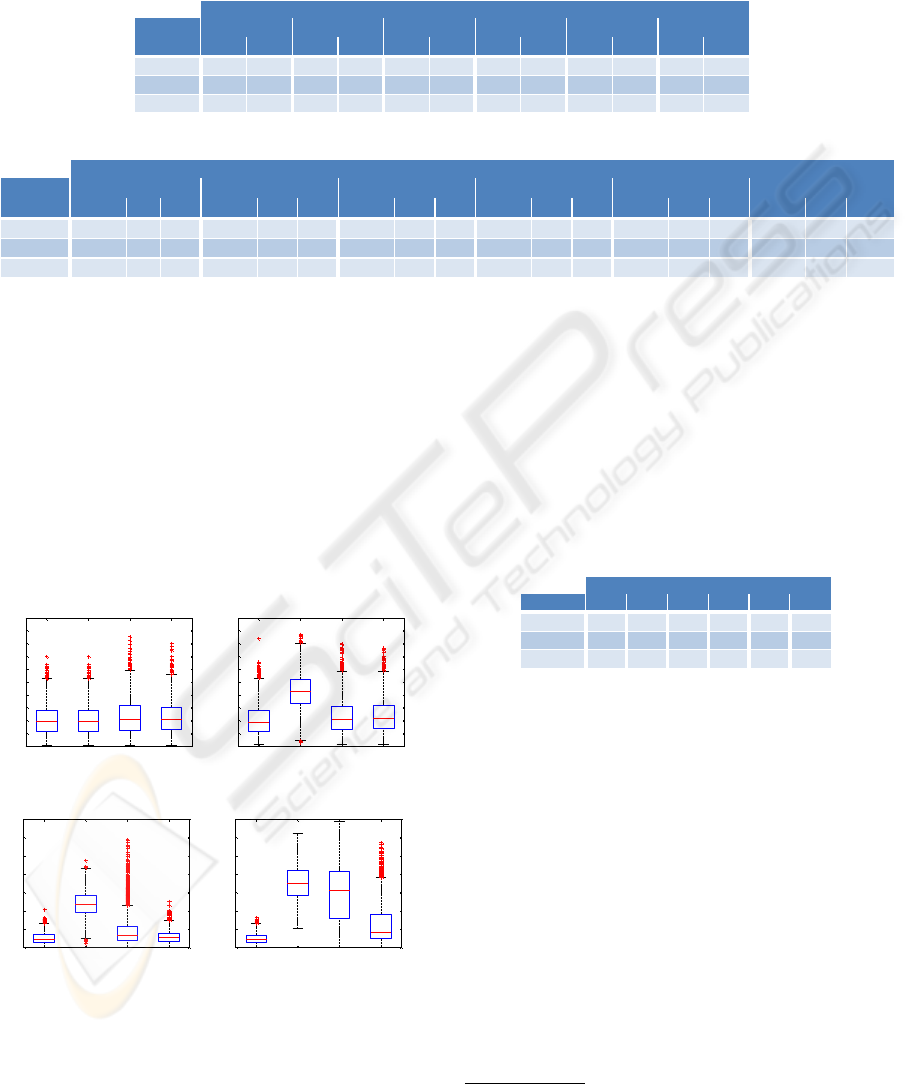
Table 2: Comparison of the reconstruction errors of the standard PCA, the R-PCA and the FR-PCA. (a) RMS reconstruction-
error per pixel given by mean and standard deviation. (b) RMS reconstruction-error per pixel given by robust statistics:
median, upper- and lower quartile. Those results correspond to the box-plots in Figure 5.
(a)
Occlusion
mean std mean std mean std mean std mean std mean std
PCA 9.96 5.88 21.30 7.24 34.60 11.41 47.72 14.37 70.91 19.06 91.64 19.78
R‐PCA 11.32 6.92 11.39 7.03 11.98 8.02 20.40 19.90 59.73 32.54 87.83 26.07
FR‐PCA 10.99 6.42 11.50 6.69 11.59 6.71 11.66 6.88 26.48 23.57 73.20 27.79
70%
ErrorperPixel
0% 10% 20% 30% 50%
(b)
Occlusion
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
median
Q
.25
Q
.75
PCA 9.58 5.77 14.02 21.29 16.56 26.01 34.67 27.71 42.17 47.24 38.22 57.42 70.45 57.03 84.54 89.49 77.55 106.15
R‐PCA 10.54 6.39 15.81 10.63 6.50 15.76 10.95 6.60 16.16 13.83 7.96 23.13 62.76 32.47 82.98 87.80 70.64 104.99
FR‐PCA 10.46 6.57 15.15 10.97 6.96 15.88 11.01 7.01 16.06 10.98 7.08 16.10 17.25 9.75 36.33 75.04 56.84 92.61
ErrorperPixel
0% 10% 20% 30% 50% 70%
ble 1.
A 5-fold cross-validation is performed for each
object category, resulting in 80% training- and 20%
test data, corresponding to 21 test images per iter-
ation. The experiments are accomplished for sev-
eral levels of spatially coherent occlusions. To sum
up, 2100 reconstructions are executed for every level
of occlusion. Quantitative results for the root-mean-
squared (RMS) reconstruction-error per pixel are
given in Table 2. In addition, in Figure 5 we show
box-plots of the RMS reconstruction-error per pixel
for different levels of occlusions.
PCA w/o occ. PCA R-PCA FR-PCA
0
5
10
15
20
25
30
35
40
45
50
Error per pixel
0% Occlusion
(a)
PCA w/o occ. PCA R-PCA FR-PCA
0
5
10
15
20
25
30
35
40
45
50
Error per pixel
10% Occlusion
(b)
PCA w/o occ. PCA R-PCA FR-PCA
0
20
40
60
80
100
120
140
E
rror per p
i
xe
l
30% Occlusion
(c)
PCA w/o occ. PCA R-PCA FR-PCA
0
20
40
60
80
100
120
140
E
rror per p
i
xe
l
50% Occlusion
(d)
Figure 5: Box-plots for different levels of occlusions for the
RMS reconstruction-error per pixel. PCA without occlu-
sion is shown in every plot for the comparison of the robust
methods to the best feasible reconstruction result.
Starting from 0% occlusion, all subspace methods
exhibit nearly the same RMS reconstruction-error. In-
creasing the portion of occlusion, the standard PCA
shows large errors whereas the robust methods are
still comparable to the PCA without occlusion (best
feasible case). The FR-PCA presents the best perfor-
mance of the robust methods over all occlusion levels.
Finally, we evaluated the runtimes
1
for the ap-
plied different PCA reconstruction methods, which
are summarized in Table 3. It can be seen that com-
Table 3: Runtime comparison. Compared to R-PCA, FR-
PCA speeds-up the computation by a factor of 18.
Occlusion 0% 10% 20% 30% 50% 70%
PCA 0.006 0.007 0.007 0.007 0.008 0.009
R‐PCA 6.333 6.172 5.435 4.945 3.193 2.580
FR‐PCA 0.429 0.338 0.329 0.334 0.297 0.307
MeanRuntime[s]
pared to R-PCA using FR-PCA speeds up the robust
reconstruction by a factor of 18! If more eigenvec-
tors are used or if the size of the images increases,
the speed-up factor gets even larger. This drastic
speed-up can be explained by the fact that the re-
finement process is started from a set of data points
mainly consisting of inliers. In contrast, in (Leonardis
and Bischof, 2000) several point sets (hypotheses)
have to be created. The iterative procedure has to
run for every set resulting in a poor runtime perfor-
mance. To decrease the runtime the number of hy-
potheses or the number of initial points has to be re-
duced, which decreases reconstruction accuracy sig-
nificantly. However, the runtime of our approach only
depends slightly on the number of starting points, thus
having nearly constant execution times. Both algo-
rithms’ runtime performance depend on the number
1
The runtimes are measured in MATLAB using an In-
tel Xeon processor running at 3GHz. The resolution of the
images is 192x144 pixels.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
134

of eigenvectors used and their length. Increasing one
of those values, the gap between the runtimes is even
getting larger.
3 ROBUST AAM FITTING
3.1 Active Appearance Model
The Active Appearance Model (AAM) (Cootes et al.,
2001) describes the variation in shape and texture of
a training set representing an object. By applying
PCA to the shape, texture, and the combination of
shape and texture, the modes of variation are calcu-
lated. By keeping solely a certain percentage of the
eigenvalue energy spectrum the model can be repre-
sented very compactly and optimally regarding Gaus-
sian noise. The AAM model fitting is performed in a
gradient descent optimization scheme. The cost func-
tion is defined as the L
2
norm of the intensity dif-
ferences (between the estimated model and the given
test image). To efficiently approximate the Jacobian
of the cost function a learned regression model is
used that describes the relationship between param-
eter updates and texture residual images according
to (Cootes et al., 2001). A local minimum of the
cost function corresponds to a model fitting solution.
Since the minimum is local and the parameter space
is high dimensional, multi-resolution techniques have
to be incorporated and the fitting requires a coarse ini-
tialization.
3.2 Robust Fitting
Since the parameter updates for the fitting process
are estimated from the texture’s residual, the standard
AAM is not robust against occlusions. To overcome
this limitation, we propose to use our FR-PCA, intro-
duced in Section 2, as a pre-processing step to remove
disturbances in the input image and to perform the
AAM fitting on the thus obtained reconstruction. Oc-
clusions can not only be of artificial spatially coherent
nature, which were taken for the quantitative evalua-
tion of the FR-PCA (Section 2), but also in case of
facial images beards or glasses. Those disturbances
of facial images influence the quality of the fitting
process of AAMs. Thus, for the pre-processing step
we trained the FR-PCA using facial images which do
not exhibit any disturbances, i.e., no beards and no
glasses.
Figure 6, which was taken from the Caltech Faces
data set (Caltech, 1999), demonstrates the whole pro-
cessing chain for robust AAM fitting under occlusion.
Figure 6(b) shows the initialization of the AAM on
the occluded input image. The rough initialization of
the AAM is done using a Viola-Jones face detection
approach (Viola and Jones, 2004), several AdaBoost-
based classifiers for locating eyes and mouth, and a
face candidate validation scheme to robustly locate
the rough face position.
Figure 6(c) demonstrates the converged fit of the
AAM on the occluded image which failed totally. In
contrast, using the FR-PCA as a pre-processing step
results in the converged fit exhibited in Figure 6(d).
In Figure 6(e), the shape from the fitting process on
the reconstructed image is overlayed on the original
input image. It can be clearly seen that the AAM can
not handle occlusions directly whereas the fit on the
reconstructed image is well defined.
(a) (b)
(c) (d) (e)
Figure 6: Handling of occlusions for AAM fitting. (a) Test
image. (b) Initialization of the AAM on the occluded im-
age. (c) Direct AAM fit on occluded image. (d) AAM fit on
reconstructed image. (e) Shape from (d) overlayed on the
test image. Image taken from Caltech Faces data set (Cal-
tech, 1999).
3.3 Experimental Results
We trained a hierarchical AAM for facial images on
three resolution levels (60x80, 120x160, 240x320).
Our training set consists of 427 manually annotated
face images taken from the Caltech face database
(Caltech, 1999) and our own collection. Taking also
the mirrored versions of those images doubles the
amount of training data. For model building we keep
90% of the eigenvalue energy spectrum for the lower
two levels and 95% for the highest level to represent
our compact model.
As described in Section 3.2, we use the FR-PCA
as a pre-processing step and perform the AAM fitting
on the reconstructed images. Hence, we trained the
ACTIVE APPEARANCE MODEL FITTING UNDER OCCLUSION USING FAST-ROBUST PCA
135

Table 4: Point-to-Point error. Comparing the direct fit of the AAM on the test image to the AAM fit utilizing the FR-PCA
pre-processing (point errors are measured on 240x320 facial images).
Occlusion
mean std mean std mean std mean std mean std
AAM 4.05 5.77 12.06 11.25 15.19 12.78 18.76 14.89 18.86 13.94
AAM+FR‐PCA 5.47 4.97 5.93 5.41 6.06 5.27 9.31 8.75 11.33 9.25
Point‐PointError
0% 10% 20% 30% 40%
FR-PCA (Section 2.1) using facial images which do
not exhibit any disturbances, i.e., no beards and no
glasses. The variance retained for the whole subspace
and for the sub-subspaces is 95%.
A 5-fold cross validation is performed using
the manually annotated images, resulting in 80%
training- and 20% test data per iteration. For each
level of occlusion, 210 AAM fits are executed. Ta-
ble 4 shows the point-to-point error (Euclidean dis-
tance of converged points to the annotated points)
comparing the direct AAM fit on the occluded im-
age to the AAM fit utilizing the FR-PCA pre-
processing. Starting from 0% occlusion, the error for
the AAM + FR-PCA is slightly larger than the direct
fit, because of the unavoidable reconstruction-blur re-
sulting from the FR-PCA reconstruction. When in-
creasing the size of the occlusion, the big advantage
of the FR-PCA pre-processing can be seen.
Up to now, to have a steerable environment, we
used artificial spatially coherent occlusions. To show
the advantage of FR-PCA pre-processing also on nat-
ural occlusions such as tinted glasses, occlusions
caused by wearing a scarf or by disturbances like
beards, Figure 7 depicts some AAM fits on images
taken from the AR face database (Martinez and Be-
navente, 1998). In addition, Figure 8 shows an il-
lustrative result on our own database. The FR-PCA
pre-processing step takes around 0.69s per image
(150x200) measured in MATLAB using an Intel Xeon
processor running at 3GHz.
4 CONCLUSIONS
The contribution of this paper is twofold. First, we
presented a robust method for AAM fitting. In con-
trast to existing approaches the robustness is not in-
cluded in the fitting step but is detached in a pre-
processing step. The main idea is to robustly re-
construct unreliable data points (i.e., occlusions) in
the pre-processing step and to use the thus obtained
undisturbed images as input for a standard AAM fit-
ting. To speed up this robust pre-processing step, as
the second contribution, we developed a novel fast ro-
bust PCA method. The main idea is to estimate a large
Figure 7: Examples of AAM fits on natural occlusions like
tinted glasses or wearing a scarf. (First column) Test images
with AAM initialization. (Second column) Direct AAM fit
on the test images. (Third column) AAM fit utilizing the
FR-PCA pre-processing. Images are taken from the AR
face database (Martinez and Benavente, 1998).
number of small PCA sub-subspaces from a sub-set of
points in parallel. By discarding those sub-subspaces
with the largest errors the number of outliers in the in-
put data can be reduced, which drastically decreases
the computational effort for the robust reconstruction.
In the experiments, we showed that our new fast ro-
bust PCA approach outperforms existing methods in
terms of speed and accuracy. In addition, the whole
process chain (robust pre-processing and AAM fit-
ting) was demonstrated in the field of face normal-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
136

Figure 8: Examples of AAM fits on natural occlusions like
beards.
ization in the presence of artificial and natural occlu-
sion noise. The results show that our robust approach
can handle such situations considerably better than a
non-robust approach. Moreover, due to the very effi-
cient robust pre-processing the proposed robust AAM
fitting method is applicable in practice for real-time
applications. An immediate idea for future work is
the investigation of how to incorporate the FR-PCA
approach directly into the AAM fitting procedure.
ACKNOWLEDGEMENTS
This work has been funded by the Biometrics Cen-
ter of Siemens IT Solutions and Services, Siemens
Austria. In addition, this work was supported by
the FFG project AUTOVISTA (813395) under the
FIT-IT programme, and the Austrian Joint Research
Project Cognitive Vision under projects S9103-N04
and S9104-N04.
REFERENCES
Beichel, R., Bischof, H., Leberl, F., and Sonka, M. (2005).
Robust active appearance models and their application
to medical image analysis. IEEE Trans. Med. Imag.,
24(9):1151– 1169.
Black, M. J. and Jepson, A. D. (1996). Eigentracking: Ro-
bust matching and tracking of articulated objects using
a view-based representation. In Proc. ECCV, pages
329–342.
Blanz, V. and Vetter, T. (1999). A morphable model for the
synthesis of 3d-faces. In Proc. SIGGRAPH.
Blanz, V. and Vetter, T. (2003). Face recognition based on
fitting a 3D morphable model. IEEE Trans. PAMI,
25(9):1063–1074.
Caltech (1999). Caltech face database.
www.vision.caltech.edu/html-files/archive.html.
Cootes, T. F., Edwards, G. J., and Taylor, C. J. (2001).
Active appearance models. IEEE Trans. PAMI,
23(6):681–685.
Dornaika, F. and Ahlberg, J. (2002). Face model adaptation
using robust matching and active appearance models.
In Proc. IEEE Workshop on Applications of Computer
Vision.
Du, C. and Su, G. (2005). Eyeglasses removal from facial
images. Pattern Recognition Letters, 26(14):2215–
2220.
Edwards, G. J., Cootes, T. F., and Taylor, C. J. (1999). Ad-
vances in active appearance models. In Proc. ICCV,
pages 137–142.
Geusebroek, J. M., Burghouts, G. J., and Smeulders, A.
W. M. (2005). The Amsterdam Library of Object
Images. International Journal of Computer Vision,
61(1):103–112.
Gross, R., Matthews, I., and Baker, S. (2006). Active ap-
pearance models with occlusion. Image and Vision
Computing, 24:593–604.
Leonardis, A. and Bischof, H. (2000). Robust recognition
using eigenimages. Computer Vision and Image Un-
derstanding, 78(1):99–118.
Martinez, A. and Benavente, R. (1998). The AR face
database. Technical Report 24, CVC.
Matthews, I. and Baker, S. (2004). Active appearance mod-
els revisited. International Journal of Computer Vi-
sion, 60(2):135–164.
Mitchell, S. C., Bosch, J. G., Lelieveldt, B. P. F., van der
Geest, R. J., Reiber, J. H. C., and Sonka, M. (2001). 3-
D active appearance models: Segmentation of cardiac
MR and ultrasound images. IEEE Trans. Med. Imag.,
21:1167–1178.
Nguyen, M. H., Lalonde, J.-F., Efros, A. A., and de la Torre,
F. (2008). Image-based shaving. Computer Graphics
Forum Journal (Eurographics 2008), 27(2):627–635.
Rao, R. (1997). Dynamic appearance-based recognition. In
Proc. CVPR, pages 540–546.
Romdhani, S. and Vetter, T. (2003). Efficient, robust and
accurate fitting of a 3D morphable model. In Proc.
ICCV, volume 2.
Theobald, B.-J., Matthews, I., and Baker, S. (2006). Eval-
uating error functions for robust active appearance
models. In Proc. FGR, pages 149–154.
Viola, P. and Jones, M. J. (2004). Robust real-time face
detection. International Journal of Computer Vision,
57(2):137–154.
Yu, X., Tian, J., and Liu, J. (2007). Active appearance
models fitting with occlusion. In EMMCVPR, volume
4679 of LNCS, pages 137–144.
ACTIVE APPEARANCE MODEL FITTING UNDER OCCLUSION USING FAST-ROBUST PCA
137
