INTERPOLATORY ADAPTIVE SUBDIVISION
FOR MESH LOD EDITING
Daniele Panozzo and Enrico Puppo
Department of Computer and Information Sciences - University of Genova, Via Dodecaneso 35, 16146 Genova, Italy
Keywords:
Triangle meshes, Subdivision, Level of Detail.
Abstract:
We propose an adaptive interpolatory scheme for subdivided triangle meshes that is compliant with the modi-
fied butterfly subdivision and can be used effectively and efficiently in selective editing of meshes. Our scheme
is developed upon the RGB subdivision, an adaptive scheme that is based on the factorization of the one-to-
four triangle split pattern. We introduce the concept of topological angle and related operators to efficiently
navigate and edit an adaptively subdivided mesh. On the basis of this new scheme, we present an interactive
application that allows a user to freely edit the Level of Detail of a model starting at a base mesh.
1 INTRODUCTION
Subdivision surfaces are becoming more and more
popular in computer graphics and CAD, with primary
applications in the entertainment industry (Zorin and
Schr
¨
oder, 2000). The Loop scheme is very popular
for subdividing triangular meshes for its C
2
smooth-
ness. However, it may be not suitable to some mod-
eling contexts, such as videogames, because it dis-
places vertices by introducing a sort of “shrinking”
and “oversmoothing” on the surface. This may give
rise to unpleasant warping effects that the designer
cannot control. Details can be better preserved with
an interpolatory scheme, such as the modified butter-
fly scheme (Zorin et al., 1996).
Most often subdivision is applied up to a certain
level and, in many cases, different parts of the mesh
should be refined at different levels of detail. When-
ever a model is constrained to a certain budget of
polygons, higher LOD should be used in the prox-
imity of joints and in detailed areas. LOD editing
is a customary task in Continuous Level Of Detail
(CLOD) for free-form mesh modeling (L
¨
ubke et al.,
2002), but its extension to subdivided meshes is not
straightforward. The RGB Subdivision was intro-
duced in (Puppo and Panozzo, 2008) to support such
a task. It is an adaptive scheme for triangle meshes,
which is based on the iterative application of local re-
finement and coarsening operators and it is compliant
with the Loop subdivision.
Here, we extend such a scheme to interpolatory
subdivision and we explicitly address the interactive
editing of LOD. We propose a new set of operators
to navigate a mesh, which are based on the notion of
topological angle on an adaptively subdivided mesh.
On this basis, we develop new efficient algorithms for
stencil computation. We also present an interactive
application, developed upon our new scheme, that al-
lows a user to dynamically adjust LOD through brush
tools.
2 RELATED WORK
In this section, we will review only those works re-
lated to adaptive subdivision of triangle meshes. The
interested reader can refer to (Warren and Weimer,
2002) for a general textbook on subdivision sur-
faces. Red-green triangulations (Bank et al., 1983)
are popular in the common practice to obtain con-
forming adaptive meshes from hierarchies generated
from one-to-four triangle split. Variants of red-green
triangulations were proposed in (Pakdel and Sama-
vati, 2007; Zorin et al., 1997) in a modeling con-
text to comply with either the Loop, or the butterfly
subdivision. Apparently, such mechanisms were not
designed to support interactive editing, but rather for
“one shot” operations. Some other proposals exist to
factorize the one-to-four triangle refinement scheme
into atomic local operations, with the aim to support
editing of adaptive subdivisions (Seeger et al., 2001;
Velho, 2003). The
√
3 subdivision (Kobbelt, 2000)
70
Panozzo D. and Puppo E. (2009).
INTERPOLATORY ADAPTIVE SUBDIVISION FOR MESH LOD EDITING.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 70-75
DOI: 10.5220/0001769900700075
Copyright
c
 SciTePress

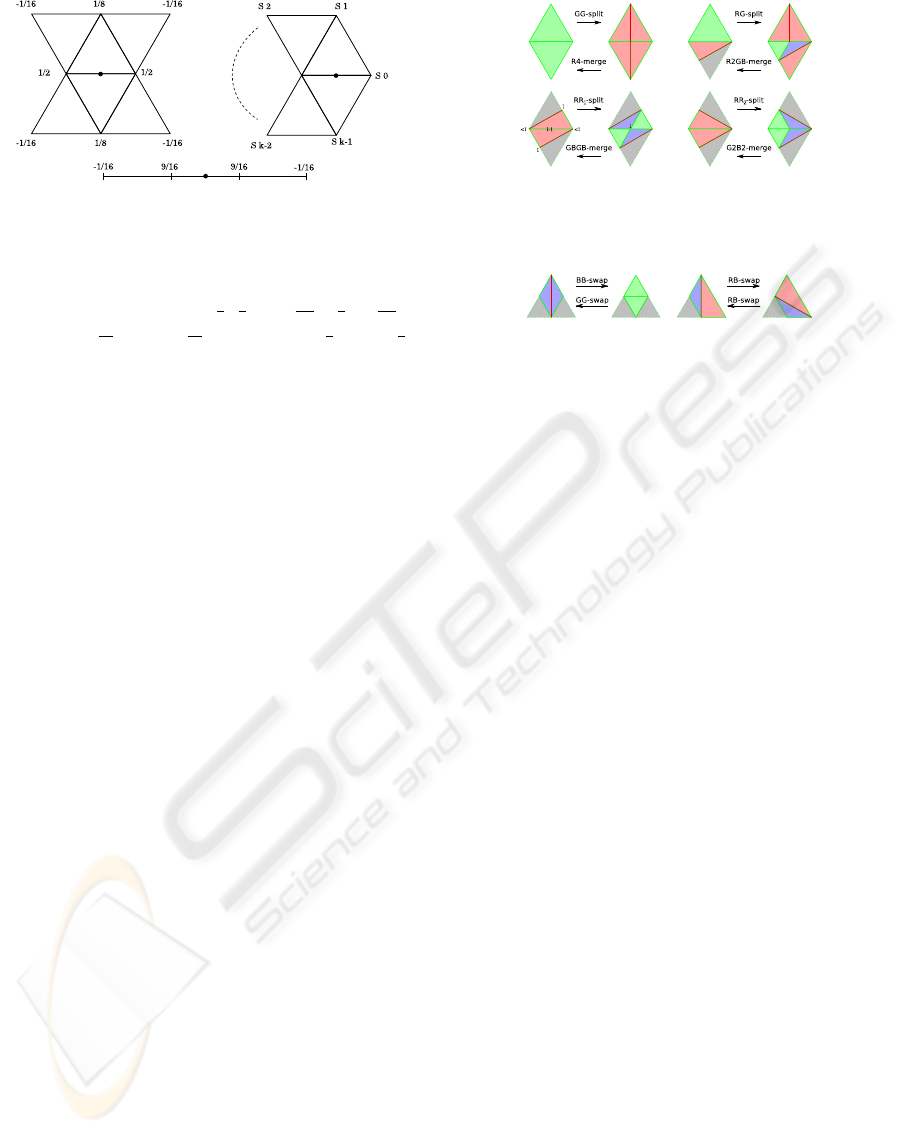
Figure 1: Stencils for the modified butterfly subdivision
scheme: stencil for splitting an internal edge that has both
endpoints at regular vertices (top-left); stencil for splitting
an internal edge incident at an extraordinary vertex (top-
right); stencil for splitting a boundary edge (bottom). The
coefficients s
i
are: for k > 5,
1
k

1
4
+ cos
2iπ
k
+
1
2
cos
4iπ
k

;
for k = 3, s
0
=
5
12
, s
1,2
= −
1
12
; for k = 4, s
0
=
3
8
, s
2
= −
1
8
,
s
1,3
= 0.
and the 4-8 subdivision (Velho and Zorin, 2001)
schemes are based on alternative subdivision patterns.
They are naturally adaptive, being both based on lo-
cal conforming operators, and they both address the
correct relocation of vertices at the cost of some over-
refinement.
3 BACKGROUND
3.1 Triangle Meshes
A triangle mesh is a triple Σ = (V, E, T ) where: V is a
set of points in 3D space, called vertices; T is a set of
triangles having their vertices in V and such that any
two triangles of T either are disjoint, or share exactly
either one vertex or one edge; E is the set of edges of
the triangles in T . Standard topological incidence and
adjacency relations are defined over the entities of Σ.
We will assume to deal always with manifold meshes
either with or without boundary.
3.2 Modified Butterfly Subdivision
The modified butterfly subdivision scheme, proposed
in (Zorin et al., 1996), is based on the one-to-four tri-
angle split pattern and it is an interpolatory scheme
converging to a C
1
limit surface. The position of a
new vertex inserted by subdivision is computed as a
weighted average of the positions of vertices in a sten-
cil in the neighborhood of the split edge. The stencils
for the standard cases, together with the weights used
to compute the average, are shown in Figure 1. For the
sake of brevity, we do not report here additional sten-
cils for edges in the proximity of boundary or crease
Figure 2: Edge split and edge merge operators. Labels
denote the level of vertices and edges.
Figure 3: Edge swap operators.
edges. The algorithms that we provide in Section 5
are sufficient to fetch vertices of such stencils as well.
4 RGB TRIANGULATIONS
RGB triangulations have been defined in (Puppo and
Panozzo, 2008) and provide a progressive mechanism
for the refinement of a mesh through operators for lo-
cal modification. The essential idea is to provide op-
erators that modify a mesh by either introducing or
deleting one vertex at a time and that can be used to
factorize the one-to-four triangle split pattern and its
reverse. Given a base mesh, we assign level zero to
all its vertices, edges and triangles, and color green
to all its edges and triangles. The color and level of
triangles and edges in a subdivided mesh is defined
inductively by the application of the eleven local op-
erators depicted in Figures 2 and 3.
Edge split operators take an edge e at level l and
split it by inserting a new vertex, at level l + 1, at the
midpoint of e. This induces the simultaneous bisec-
tion of triangles t
0
and t
1
incident at e, which may
come in the following variants (see Figure 2):
• GG-split: t
0
and t
1
are both green. The bisec-
tion of each triangle t
0
and t
1
at the midpoint of e
generates two red triangles at level l. Each such
triangle will have: a green edge at level l, a green
edge at level l + 1 and a red edge at level l.
• RG-split: t
0
is green and t
1
is red. Triangle t
0
is
bisected as above. Bisection of t
1
generates a blue
triangle at level l and a green triangle at level l +1.
• RR-split: t
0
and t
1
are both red. Triangles t
0
and t
1
are both bisected as t
1
in the previous case.
There are two variants: RR
1
-split and RR
2
-split,
INTERPOLATORY ADAPTIVE SUBDIVISION FOR MESH LOD EDITING
71

which can be recognized by the cycle of colors on
the boundary of the diamond formed by t
0
and t
1
.
Edge merge operators reverse edge split and can be
applied to triangles incident at vertices of valence
four. The same cases depicted in Figure 2 occur
(modifications apply right-to-left in this case): R4-
merge inverts GG-split; R2GB-merge inverts RG-
split; GBGB-merge inverts RR
1
-split; G2B2-merge
inverts RR
2
-split. Edge swap operators take a quadri-
lateral formed by a pair of adjacent triangles and swap
its diagonal. They are defined as follows (see Figure
3):
• BB-swap takes a pair of blue triangles at level l,
which are adjacent along a red edge at level l, and
produces a pair of green triangles at level l + 1;
• GG-swap, which inverts BB-swap, takes a pair of
adjacent green triangles t
0
and t
1
at level l > 0 if
one of them has all three vertices at level l, and
produces a pair of blue triangles adjacent along a
red edge;
• RB-swap takes a pair formed by a red and a blue
triangle at the same level l of subdivision, which
are adjacent along a red edge, and produces an-
other red-blue pair of triangles at level l.
An edge e at level l ≥ 0 can split if and only if it is
green and its two adjacent triangles t
0
and t
1
are both
at level l. Red edges can just swap. Combinations
of merge and swap operators can remove a vertex v
at level l > 0, without removing other vertices, if and
only if all vertices adjacent to v are at level ≤ l. With
the above operators at hand, a mesh can be refined and
coarsened progressively.
5 RGB SUBDIVISION WITH THE
MODIFIED BUTTERFLY
Given the above framework for refining and coarsen-
ing meshes, it follows that any RGB triangulation will
contain just vertices that also appear in the (virtual
and infinite) family of meshes generated through re-
cursive one-to-four triangle split. In order to obtain an
adaptive subdivision scheme compliant with the mod-
ified butterfly, we must guarantee that the position in
3D space assigned to each vertex is the same in the
RGB subdivision and in a standard modified butterfly
subdivision. In order to do this, it is sufficient to guar-
antee that, during a split operation, we always retrieve
the vertices in the standard stencil and their positions.
Since a RGB mesh is adaptive, given an edge e at level
l to split, two opposite situations may occur:
(a) (b)
Figure 4: (a) Some triangles in the stencil have been refined
beyond the level of the splitting edge. (b) Some triangles in
the stencil are at a level lower than that of the splitting edge
(marked with a red bullet).
• Some triangles of the stencil have been refined at
levels > l. In the area spanned by the stencil, such
refinement can be of arbitrarily many levels, and
it is necessary to navigate the mesh, starting at e,
to fetch the vertices of the stencil (see Figure 4a).
• Some triangles of the stencil are at a level < l.
This means that some vertices in the stencil may
not belong to the current mesh (see Figure 4b). In
this case, we perform all the necessary splits to
introduce the required vertices, and we mark such
additional vertices as “overrefined”. When the en-
tire refining process is completed (not just a single
split, but rather a batch of subdivision operations)
a cleanup is performed, in which we apply coars-
ening operations to remove all vertices that result
overrefined with respect to current LOD.
In the following subsections, we develop the nec-
essary techniques and algorithms to identify the sten-
cils.
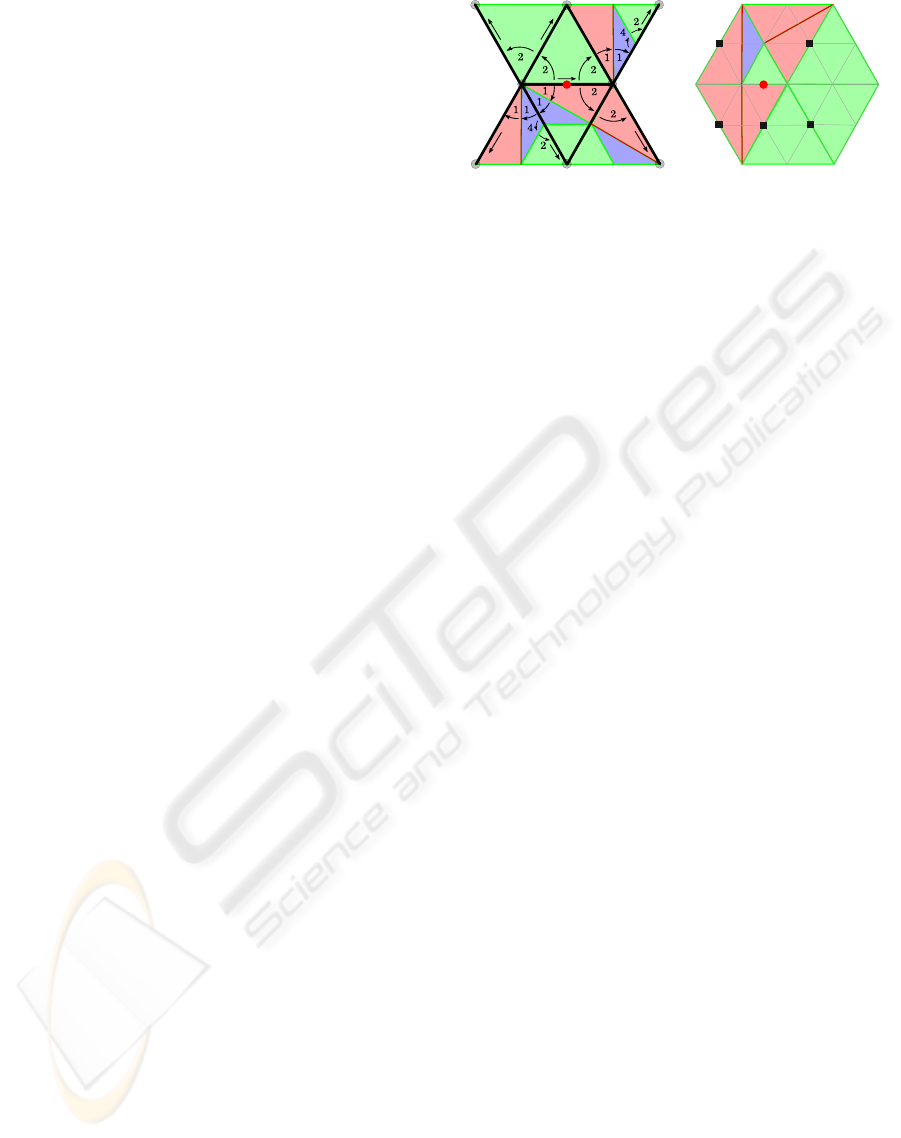
5.1 Topological Angle Definition
We assign a topological width to the angles of every
triangle in an RGB triangulation using the following
rules (see Figure 5):
1. Green Triangle: each angle has a topological
width of 2;
2. Red Triangle: the angle opposite to the red edge
has topological width of 2; the angle opposite to
the edge at the highest level has topological width
of 1; and the remaining angle has a topological
width of 3;
3. Blue Triangle: The angle opposite to the red edge
has topological width of 4; the other two angles
have topological width of 1.
An angle with topological width of 6 is said to be
flat. Such values are not related to geometrical values,
except when all green triangles are equilateral: only in
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
72

Figure 5: Topological angles: the angle value is assigned
to each vertex in each triangle.
that case, a topological width of 1 corresponds to 30
degrees. We do not need to store angle widths in the
data structure since they can be extracted using colors
of triangles and edges, and the level of vertices.
We now prove some invariants on angles that will
be useful for mesh navigation.
Lemma 5.1. If an edge e is split into two edges e
0
and e
1
by adding a vertex v, both angles formed by e
0
and e
1
are flat.
Proof. The only possible ways to split an edge are de-
picted in Figure 2. By comparing the triangles in such
figures with the definitions of angles given above, and
depicted in Figure 5, it is readily seen that in all cases
the sum of angles on each side of the pair e
0
e
1
is
6.
Lemma 5.2. The width of a topological angle be-
tween a pair of edges is invariant upon editing op-
erations on the mesh.
Proof. Consider a pair of edges e and e
0
incident at
v and one of the two angles they form at v. It is suf-
ficient to analyze editing operations that affect trian-
gles spanned by such an angle. For each such trian-
gle t, there are three possible cases, which are readily
verified by comparing Figures 2 and 5: If the editing
operation neither splits t with an edge incident at v,
nor merges t with an adjacent triangle around v, then
the angle of t at v is unchanged; If the angle of t at
v is split into two angles, then sum of widths of such
angles is equal to the width of the angle of t at v be-
fore split (this occurs in split and swap operations);
If t is merged with another triangle t
0
adjacent to it
around v, by deleting their common edge, then either
e and e
0
are merged into a single edge (this occurs in
merge operations only), or the width of angle at v of
the new triangle is equal to the sum of widths of an-
gles of t and t
0
at v (this occurs in merge and swap
operations).
Lemma 5.3. No matter how an edge e is subdivided
into a chain of edges e
0
, . . . , e
k
, angles between two
consecutive edges e
i−1
and e
i
, i = 1, . . . , k are flat.
Proof. The proof follows from the above two lem-
mas by noting that every split produces flat angles and
such angles are invariant upon subsequent editing op-
erations.
5.2 Encoding and Navigating a RGB
Triangulation
We now provide a set of primitive operations that al-
low us to move in a RGB triangulation, which will
be used to fetch the vertices of stencils. We define
switch operators similar to those proposed in (Bris-
son, 1993), plus two new operators, called rotate and
move, that are specific for the RGB triangulation.
All the operators use a unique identifier, that we
call pos, of position in the triangulation. The identi-
fier contains a vertex v, an edge e incident at v, and a
face f bounded by e. Given a pos p, we will denote
by p.v, p.e and p.f its related vertex, edge and face,
respectively.
1. p.switchVertex(): moves to a pos having the
same edge and face of p, and the other vertex of
p.e with respect to p.v.
2. p.switchEdge(): moves to a pos having the same
vertex and face of p, and the other edge incident
at both p.v and p.f with respect to p.e.
3. p.switchFace(): moves to a pos having the same
vertex and edge of p, and the other face incident
at p.e with respect to p.f.
4. p.rotate(i): executes an alternate sequence of
p.switchEdge() and p.switchFace() operators un-
til a topological angle of width i has been scanned.
5. p.move(l): executes an alternate sequence
of p.switchVertex(), p.rotate(6) and
p.switchFace() operators until a vertex with
level ≤ l is reached. This primitive stops as soon
as the vertex is reached.
The invariance lemmas proved in the previous sec-
tion guarantee that, starting at a splitting edge p.e at
level l, we can navigate the mesh by moving to ad-
jacent triangles of the stencil at level l (through a
p.rotate(2) operation) and we can follow chains of
edges until we reach the other end of an edge at level
l (through a p.move(l) operation).
A standard topological data structure for triangle
meshes (representing at least vertices and triangles) is
sufficient to support the operations described above.
Note that the management of RGB triangulations does
not need to store any hierarchy. It is just sufficient to
add the following fields to the standard data structure:
for each vertex: its level of insertion (one byte); for
each edge (if represented in the data structure): its
color and level (one byte); for each triangle: its color
and level (one byte). Therefore, the overhead with
INTERPOLATORY ADAPTIVE SUBDIVISION FOR MESH LOD EDITING
73

respect to a standard topological data structure is neg-
ligible.
5.3 Algorithms to Identify the Stencils
Using the previous primitives, it is easy to fetch all
vertices of a stencil. The algorithm takes as input a
pos p, where p.e identifies the edge to split. In the reg-
ular case, two vertices of the standard butterfly stencil
are immediately available (i.e., the endpoints of the
splitting edge). The remaining vertices of stencil are
fetched navigating the mesh through the algorithm de-
scribed in the following.
Algorithm 1: fetchRegularStencil(Pos. pos)).
1: list<Vertex> stencil;
2: Pos pos2 = pos;
3: int maxlevel = maxVertexLevel(pos);
4: pos2.switchVertex();
5: stencil.add(pos.v);
6: stencil.add(pos2.v);
7: splitEdgesIfNeeded(pos.v,maxlevel,STD);
8: splitEdgesIfNeeded(pos2.v,maxlevel,STD);
9: pos2 = pos;
10: pos2.switchFace();
11: fetchHalf(pos,stencil);
12: fetchHalf(pos2,stencil);
13: return stencil;
Algorithm 2: fetchHalf(Pos. pos,
list<Vertex> stcl).
1: Pos p;
2: p = pos;
3: p.rotate(2);
4: p.move(maxlevel);
5: stcl.add(p.v);
6: p = pos;
7: p.rotate(4);
8: p.move(maxlevel)
9: stcl.add(p.v);
10: p = pos;
11: p.switchVertex();
12: p.rotate(4);
13: p.move(maxlevel)
14: stcl.add(p.v);
Function maxVertexLevel(p) returns the highest
level of the two vertices incident at p.e. Function
splitEdgesIfNeeded(v,l,type) checks if the neighbor
vertices of the vertex v at level l are present. If not, it
performs recursive split operations to add them. The
function looks at the incident edges and splits every
edge of level < l. In case an edge is red, since it
cannot split directly, it is necessary to split the lowest
green edge of every red triangle incident at it, and ap-
ply a BB-swap next. vertices checked depend on the
value of parameter type, which is related to the type
of stencil analyzed: in case this value is STD, only
the four neighbors found by pivoting around v with
rotations of width 2 and 4, respectively, are checked;
in case the value is BOUND, just the neighbor along
the boundary is checked; in case the value is EX-
TRA, all neighbors of v are checked. Function fetch-
Half finds the upper/lower vertices in the stencil. The
identification of the stencil in the extraordinary case
is similar. The extensions of the previous algorithms
to boundary cases is straightforward. The complex-
ity of fetching a stencil is bounded from above by the
length of chains of edges, i.e., by the maximum num-
ber of times an edge at level l adjacent to the splitting
edge has been subdivided. In the worst case, this num-
ber can be linear in the size of the mesh, but this oc-
curs only in pathological situations where the mesh is
highly refined only around a vertex and it abruptly de-
grades to the base level elsewhere. In practical cases,
chains are usually quite short. So, these algorithms
can be considered to run in constant time on average.
6 INTERACTIVE EDITING OF
LOD
On the basis of our RGB subdivision, we have de-
veloped an interactive application that allows a user
to start with a base mesh and edit its LOD by using
two tool brushes to increase and decrease detail lo-
cally, according to her/his needs. Our application is
a prototype implemented as a plugin for MeshLab, an
open source tool for processing, editing and visual-
izing 3D triangular meshes (Meshlab, 2008). A beta
version of the software can be currently downloaded
from http://ggg.disi.unige.it/rgbtri/.
We have tested our tool on a number of mod-
els representing various objects. Most objects were
described with base meshes in the order of 10
2
-10
4
faces, which have been selectively refined up to sizes
of order 10
6
. In Figure 6 we present some results and
we show some comparisons between the butterfly and
the Loop RGB subdivisions. The mesh refined with
the Loop subdivision results smoother than the mesh
refined with the butterfly subdivision, but the shape is
severely warped near the eyes, nose and chin.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
74

Figure 6: The base mesh (top); the same mesh refined on
the eyes, nose and hair tufts at level 3, using the the butterfly
scheme (middle); the same mesh refined in the same way
with the Loop scheme (bottom).
7 CONCLUSIONS
The RGB subdivision scheme has several advantages
over both classical and adaptive subdivision schemes,
as well as over CLOD models: it supports fully dy-
namic selective refinement while remaining compli-
ant with standard schemes; it is better adaptive than
previously known schemes based on the one-to-four
triangle split pattern; it does not require hierarchical
data structures; mesh editing can be implemented ef-
ficiently by plugging faces inside the mesh, according
to rules encoded in lookup tables, thus avoiding cum-
bersome procedural updates.
A similar approach can be undertaken also to de-
velop hybrid tri-quad adaptive meshes for the selec-
tive refinement of quad meshes. These extensions are
the subject of our current and future work. We be-
lieve that this approach to adaptive subdivision may
give valid substitutes or complements to standard sub-
division for solid modelers and simulation systems.
Combined with reverse subdivision techniques, it may
also offer a valid alternative to CLOD models for free-
form objects in computer graphics.
A crucial feature to support modeling is the ability
to edit the position of vertices of the control mesh and
propagate this consistently on the subdivided mesh.
This should be easy on the butterfly RGB subdivision:
when a vertex of the control mesh is moved, its effects
are propagated through the network of edges to ver-
tices having that vertex in their mask. The navigation
primitives that we have defined in Section 5.2, can be
used effectively to this purpose. In the future, we plan
to develop these features and to integrate our scheme
in the Blender (Blender, 2008) solid modeler, which
offers an open source platform that can be extended
by external plugins.
REFERENCES
Bank, R., Sherman, A., and Weiser, A. (1983). Refinement
algorithms and data structures for regular local mesh
refinement. In Stepleman, R., editor, Scientific Com-
puting, pages 3–17. IMACS/North Holland.
Blender (2008). http://www.blender.org/.
Brisson, E. (1993). Representing geometric structures in d
dimensions: Topology and order. Discrete and Com-
putational Geometry, 9:387–426.
Kobbelt, L. (2000).
√
3 subdivision. In Proceedings ACM
SIGGRAPH 2000, pages 103–112.
L
¨
ubke, D., Reddy, M., Cohen, J., Varshney, A., Watson,
B., and H
¨
ubner, R. (2002). Level Of Detail for 3D
Graphics. Morgan Kaufmann.
Meshlab (2008). http://meshlab.sourceforge.net.
Pakdel, H. and Samavati, F. (2007). Incremental subdivision
for triangle meshes. International Journal of Compu-
tational Science and Engineering, 3(1):80–92.
Puppo, E. and Panozzo, D. (2008). RGB subdivi-
sion. IEEE Transactions on Visualization and
Computer Graphics. In press. Electronic version at
http: // doi.ieeecomputersociety.org / 10.1109 / TVCG.
2008.87.
Seeger, S., Hormann, K., H
¨
ausler, G., and Greiner, G.
(2001). A sub-atomic subdivision approach. In Girod,
B., Niemann, H., and Seidel, H.-P., editors, Pro-
ceedings of Vision, Modeling and Visualization 2001,
pages 77–85, Berlin. Akademische Verlag.
Velho, L. (2003). Stellar subdivision grammars. In Pro-
ceedings 2003 Eurographics/ACM SIGGRAPH Sym-
posium on Geometry Processing, pages 188–199.
Velho, L. and Zorin, D. (2001). 4-8 subdivision. Computer-
Aided Geometric Design, 18:397–427.
Warren, J. and Weimer, H. (2002). Subdivision Methods for
Geometric Design. Morgan Kaufmann.
Zorin, D. and Schr
¨
oder, P., editors (2000). Subdivision for
Modeling and Animation (SIGGRAPH 2000 Tutorial
N.23 - Course notes). ACM Press.
Zorin, D., Schr
¨
oder, P., and Sweldens, W. (1996). Interpo-
lating subdivision for meshes with arbitrary topology.
In Comp. Graph. Proc., Annual Conf. Series (SIG-
GRAPH 96), pages 189–192. ACM Press.
Zorin, D., Schr
¨
oder, P., and Sweldens, W. (1997). Interac-
tive multiresolution mesh editing. In Comp. Graph.
Proc., Annual Conf. Series (SIGGRAPH 97), ACM
Press. 259-268.
INTERPOLATORY ADAPTIVE SUBDIVISION FOR MESH LOD EDITING
75