SEGMENTATION THROUGH EDGE-LINKING

Segmentation for Video-based Driver Assistance Systems

Andreas Laika

BMW Group Forschung und Technik, Hanauer Straße 46, D-80992 M

unchen, Germany

Adrian Taruttis and Walter Stechele

Lehrstuhl Integrierte Systeme, Technische Universit

at M

unchen, Arcisstraße 21, D-80333 M

unchen, Germany

Keywords:

Segmentation, Edge linking, Driver assistance, Object recognition.

Abstract:

This work aims to develop an image segmentation method to be used in automotive driver assistance systems.

In this context it is possible to incorporate a priori knowledge from other sensors to ease the problem of local-

izing objects and to improve the results. It is however desired to produce accurate segmentations displaying

good edge localization and to have real time capabilities. An edge-segment grouping method is presented to

meet these aims. Edges of varying strength are detected initially. In various preprocessing steps edge-segments

are formed. A sparse graph is generated from those using perceptual grouping phenomena. Closed contours

are formed by solving the shortest path problem. Using test data ﬁtting to the application domain, it is shown

that the proposed method provides more accurate results than the well-known Gradient Vector Field Snakes.

1 INTRODUCTION

Video based driver assistance systems offer the po-

tential to increase safety and driver comfort in future

automotive environments. Hence, it is necessary to

develop video processing techniques that can be im-

plemented within the constraints of automotive pro-

cessing systems. Below we present a method for the

segmentation of objects in images.

Using shape-information as a feature for classiﬁ-

cation, or providing visual information to the driver

are possible applications for this approach. Spe-

ciﬁc requirements are important in this context: the

method should allow to integrate a priori knowledge

of the object, such as data obtained from other sen-

sors like a laser scanner. It should conceivably be able

to run in a real-time environment. Finally, accurate

segmentation results are desired, requiring the output

contour to closely ﬁt to the object boundary. To meet

these aims we present an algorithm based on methods

for perceptual grouping of edge-segments.

2 STATE OF THE ART

According to (Gonzalez and Woods, 1987) segmenta-

tion is the partitioning of an image into its constituent

regions or into objects and background. Segmenta-

tion can be based on the detection of discontinuities,

based on grouping similarities in color or texture or

based on other cues like motion. If the goal of the

segmentation method is to partition an image into re-

gions of similarity, many alternatives like seeded re-

gion growing or Watershed segmentation exist. Those

techniques are relatively good at their stated goal of

segmenting images into homogeneous regions, but

the goal of this work, namely segmenting complete

objects, would require an augmentation with some ad-

ditional method for grouping regions. Fundamental

to the problem of segmenting an object is the ques-

tion of how that object is deﬁned. Motion cannot be

used as a cue in the general case (e.g. when object and

background have the same relative velocity). Also, an

object is not necessarily homogeneous in color or tex-

ture. This leaves segmentation based on the object’s

saliency, i.e. how much an object stands out from its

background. Additionally in our case we assume the

presence of a region of interest (ROI) containing con-

tain exactly one object. Section 3.1 explains how such

Laika A., Taruttis A. and Stechele W. (2009).

SEGMENTATION THROUGH EDGE-LINKING - Segmentation for Video-based Driver Assistance Systems.

In Proceedings of the First International Conference on Computer Imaging Theory and Applications, pages 43-49

DOI: 10.5220/0001770700430049

 SciTePress

a ROI can be determined. While there is no quan-

tative deﬁnition of saliency, it is often considered in

terms of the principles of perceptual organization and

the laws of Gestalt psychology (Lowe, 1985). Ele-

ments are grouped together according to the phenom-

ena of Proximity, Similarity, Closure, Continuation,

Symmetry and Familiarity. Since many of the group-

ing phenomena found to be important in human visual

perception are related to discontinuities, an approach

to object segmentation based on edge detection is ap-

propriate.

Attempts at object segmentation based on grouping

of edge-segments (Elder and Zucker, 1996; Kiranyaz

et al., 2006; Wang et al., 2005; Stahl and Wang,

2007; Mahamud et al., 2003) roughly follow these

steps: First the input images are preprocessed before

running an edge detection algorithm over them, the

resulting edge maps are traced into edge-segments,

these edge-segments are further processed. Finally, a

search algorithm is applied to graph representations of

the edge-segments to ﬁnd closed contours. Some pro-

cessing steps of our method are inspired by a related

method by Ferreira, Kiranyaz, and Gabbouj (hence-

forth referred to as FKG) (Kiranyaz et al., 2006),

which in turn,has some similarities to a method by

Elder and Zucker (Elder and Zucker, 1996).

3 THE ALGORITHM

3.1 Preprocessing

Reduction to the Region of Interest (ROI). The

method starts by reducing the image to the region

of interest (ROI). Only that part of the image is

processed further. Knowledge of that ROI can ei-

ther be generated by manually labelling or by using

additional sensors like laser-scanners or PMD 3D-

cameras. They provide information about the distance

to the object, allowing a discrimination of object and

background. Then again those sensor usually have

a much lower spatial resolution. So usually only a

bounding box of the object’s position can be deter-

mined. At best a rough contour of the object at a much

lower resolution can be found.

3.2 Prominence-Map Generation

Detection of Weak and Strong Edges. In a ﬁrst

step edges of different strength are detected. The one

approach is to detect edges in different scales of a

scale space. However due to gaussian ﬁltering edges

can move . FKG uses a cascade of bilateral ﬁlters to

Figure 1: Edge maps generated with 4 different thresholds

(top) and the corresponding Prominence map (bottom).

overcome this problem, but Runtime is high and pa-

rameters are heavily dependent on the object in the

image. We generate edge maps with different levels

of detail by increasing the edge detection thresholds

of the Canny Edge Detector (Canny, 1986) in k iter-

ations. This can be viewed as an approximate dis-

cretization of edge pixel strengths.

Combining Edges to a Prominence Map. Edge

maps are then merged into a single prominence map.

Each edge pixel i

x,y

is assigned a prominence value

x,y

∈

{

1,...,k

}

corresponding to the k increasing

Canny edge detection thresholds after which that edge

pixel still remains detected as an edge. Figure 1 shows

the prominence map generated from combining edge

maps with 4 different thresholds.

Morphological Thinning. Since Canny edge de-

tection does not guarantee edge-segments with a

thickness of exactly one pixel, a thinning process is

applied to the prominence map to reduce that thick-

ness to one pixel. This simpliﬁes the subsequent edge

tracing process.

The Use of A Priori Knowledge. If additionally to

the bounding box also a rough contour of the object is

available, this is used as additional a priori knowledge

to boost the segmentation process in two ways: First

the prominence values of edge pixels in a region on

and near the contour of that mask can be increased

and are so more likely to be incorporated in the ﬁnal

contour. Second the search space can be reduced by

discarding pixels which are not in that region.

3.3 Generating a Graph Representation

Tracing of Edge-segments. The process of tracing

is the ﬁrst step in the transition from individual edge

pixels on the prominence map to a graph represen-

tation. To generate a list of edge-segments ES

∈

IMAGAPP 2009 - International Conference on Imaging Theory and Applications

{

,ES

,...,ES

}

. all edges in the prominence map

are traced.An edge-segment containing a set of L 8-

connected pixels is denoted as ES

{

,...,i

}

The two pixels with exactly one neighbor are marked

as endpoints. Pixels with two neighbors are marked as

transitional pixels. A pixel with more than two neigh-

bors is an endpoint at a junction between two or more

edge-segments. In this case one connected edge in the

prominence map is split into several edge-segments.

The prominence values corresponding to the edge

pixels are summed up to compute a prominence value

for the whole segment P

∑

x,y

∈ES

x,y

(1)

This grouping of edge pixels can be viewed as

an incorporation of the perceptual organization phe-

nomenon of proximity on the low level of edge pix-

els. edge-segments consisting of less than 3 pixels are

discarded as noise. If the tracing ﬁnds contours which

are already closed, they are stored for later considera-

tion as candidate objects (see in 3.5).

Figure 2: Junction splitting (endpoints marked in red).

Left: before, Right: after.

Junction Splitting. Figure 2 shows an edge-

segment endpoint in close proximity to a second edge-

segment. It is possible that such a conﬁguration rep-

resents the junction of three separate edge-segments.

In order to later consider each possible grouping at

such a junction, the continuous edge must be split at

the pixel closest to the existing endpoint.

Curve Splitting. As a further step in allowing many

possible groupings of edge-segments, edge segments

with curves are split iteratively until their deviation

from the straight line joining their endpoints is be-

low a certain threshold. This splitting process follows

from the grouping phenomenon of continuation. Fig-

ure 3 shows an example image section where a curved

edge-segment is split into multiple straighter edge-

segments.

Prominence Filter. In order to reduce runtime the

number of edge-segments is reduced to the N edge-

segments with the highest prominence values P

Other edge segments are discarded.

Figure 3: Curve splitting (endpoints marked in red).

Left: before; Right: after.

es0_d0

es1_d0

es2_d0

es3_d0

es3_d1

es2_d1

es1_d1

es0_d1

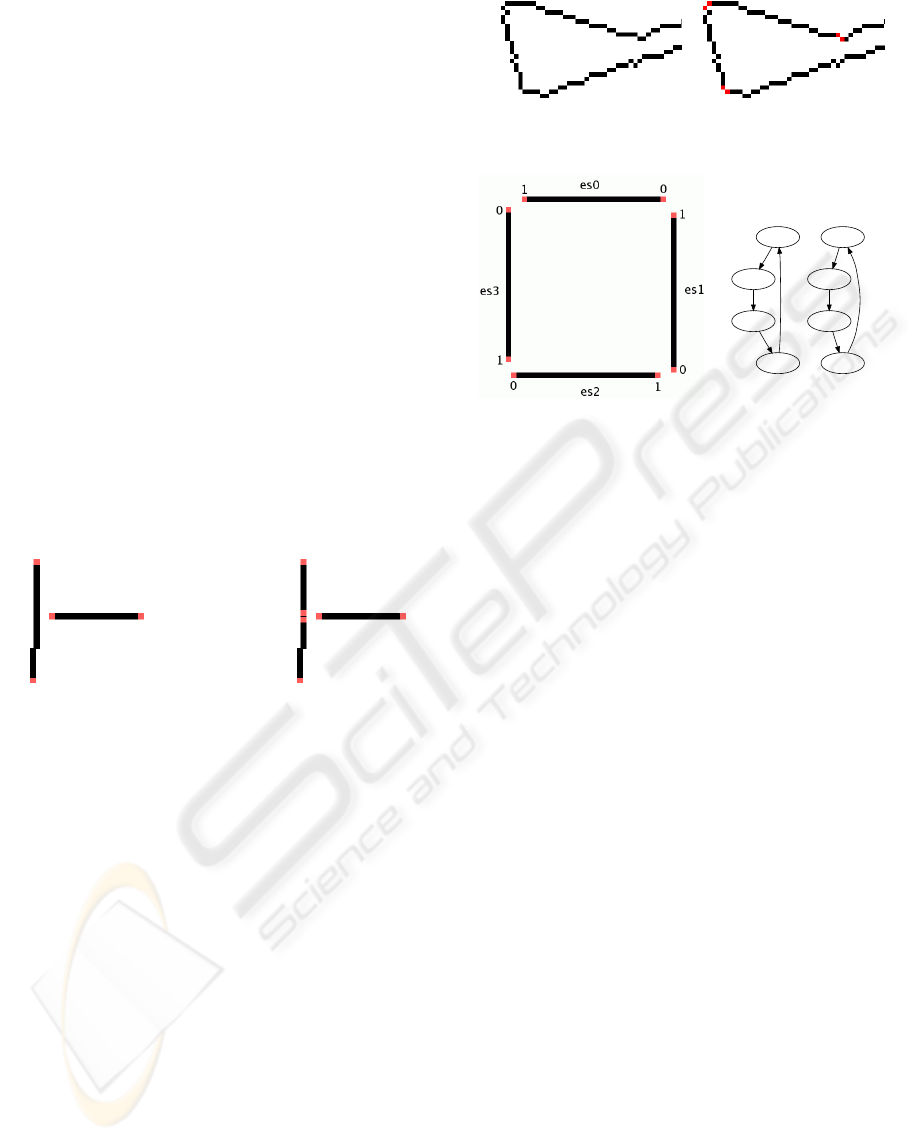
Figure 4: Left: a simple edge map with edge-segments and

ends labeled; Right: the resulting directed graph.

Linking of Edge-segments. In the previous steps

edge-segments were modiﬁed to be suitable for a

graph representation. It is however also important

how to link those segments in a graph representation.

Linking all segments with each other is not an option,

since the resulting fully connected graph makes the

search infeasible. One solution is to limit the max-

imum Euclidean distance VLL

i, j

between two end-

points i

and i

. However this leads to a high or even

complete connectivity in regions with many small

edge-segments. Few edge-segments with longer gaps

on the other hand may only be connected sparsely or

not at all. Hence we limit the number of links or ver-

tices each of the endpoints can be connected with to

an upper bound denoted V (Elder and Zucker, 1996) .

3.4 Graph-based Search

Graph Representation. For the graph representa-

tion each edge-segment is represented by two vertices

in the graph; each vertex represents an edge-segment

with virtual links leaving from one of the two end-

points of that edge-segment, in other words: each ver-

tex represents a directed edge-segment. Each virtual

link from one directed edge-segment to another is rep-

resented by a directed edge in the graph. Figure 4

shows an example edge map and the corresponding

graph representation.

Edge Weights. For a graph search to be successful

the graph’s edges need meaningful weights W

,ES

This should include both the prominence of the

edge-segment P

as well as the length of the gap

VLL. The dependence of grouping on VLL incor-

SEGMENTATION THROUGH EDGE-LINKING - Segmentation for Video-based Driver Assistance Systems

porates the grouping phenomenon of proximity.

The straight forward use of the quotient of both

,ES

= VLL

1,2

like in FKG however has

the disadvantage of implicitly including the edge-

segment’s length L

. If an edge-segment is split

at junctions or curvatures the total weight of the

resulting edges will differ from the initial weight.

Hence, we use the segment’s mean prominence. We

also raise VLL to a power, similar to (Stahl and Wang,

2007), to be able to favor longer or shorter gaps:

,ES

VLL

1,2

(2)

Search. Subsequently, Dijkstra’s algorithm is ap-

plied to search for closed contours, starting from

each of the N remaining edge-segments. The search

for salient closed contours explicitly incorporates the

grouping phenomenon of closure into the method. Di-

jkstra’s algorithm ﬁnds the shortest path from a sin-

gle source to each vertex in the graph. For ﬁnding

a closed contour the source and destination vertices

are identical, and only the lowest cost nonzero path

from the source vertex back to itself is of interest.

Additionally, since each edge-segment is represented

by two vertices depending of the direction traveled

along the edge-segment, the algorithm must ensure

that no edge-segment is traversed more than once by

the closed contour. Thus Dijkstra’s algorithm must be

adjusted in three ways:

• Terminate when the shortest path to the destina-

tion vertex is found.

• The source/destination vertex must have its dis-

tance d set to inﬁnity after the algorithm has

started so that it can be relaxed a second time.

• Relax a vertex only if the edge-segment associated

with is not on the current shortest path.

3.5 Postprocessing

Contour Selection. The best of the resulting closed

contours is selected according to the following

measure:

W =

1 +



∑

,ES

j+1



(3)

With β < 1 so that area A of the contour dominates

the ranking.

4 EVALUATION AND RESULTS

4.1 The Test Environment

The algorithm presented was implemented in C++ us-

ing the OpenCV libraries. Unless otherwise stated

the tests were run on a Linux operating system with a

2GHz Intel Core 2 Duo Processor and 2GB of RAM.

Test Data. To generate the test-data, real road

scenes were recorded through windscreen of a car

using a high-dynamic range CMOS camera. 50 im-

ages with a resolution of 752 × 480 pixel were se-

lected from those scenes. Typical objects on and

near the road, like pedestrians or cars are depicted in

those scenes. Images were not selected depending on

whether they are easy to segment or not. Some have

much detail in the immediate background or weak

edges around the object boundary. A bounding box

was deﬁned around the object of interest and a binary

segmentation mask was generated manually to serve

as ground truth for the evaluation. Two lower resolu-

tion masks were generated to simulate a priori knowl-

edge of the object shape from other sensor data, as

mentioned in 3.1.

Evaluation Method. To evaluate the results of the

segmentation method, the output segmentation mask

is compared to the ground truth mask of the manual

segmentation. Each pixel is considered separately to

give a measure of the similarity of the areas taken

up by each mask; standard methods from the ﬁeld of

pattern recognition are applied as in (Fawcett, 2004).

If an on-pixel in the output mask corresponds to an

on-pixel in the ground truth mask, it is a true positive

(T P), else a false positive (FP). If an off-pixel in the

output corresponds to an off-pixel in the ground truth,

it is a true negative (T N), else a false negative (FN).

Those numbers are used to calculate the F-measure

according to equation 4:

F-measure =

2T P

2T P + FP + FN

(4)

A threshold value of F-measure corresponding to a

subjectively good segmentation is chosen at 0.85. The

number of segmentations with a value of F-measure

above this threshold, referred to as good segmenta-

tions, is used to obtain a measure for the comparative

accurateness of the method with a particular conﬁgu-

ration.

IMAGAPP 2009 - International Conference on Imaging Theory and Applications

4.2 Inﬂuence of the Algorithm’s

Parameters

The Total Number of Edge-segments. The graph-

based search accounts with 75% for most of the run-

time which is on average 260 ms per object. Hence

the parameters inﬂuencing the search are the most im-

portant in ﬁnding a trade-off between runtime and ac-

curateness. The ﬁrst such parameter is the number

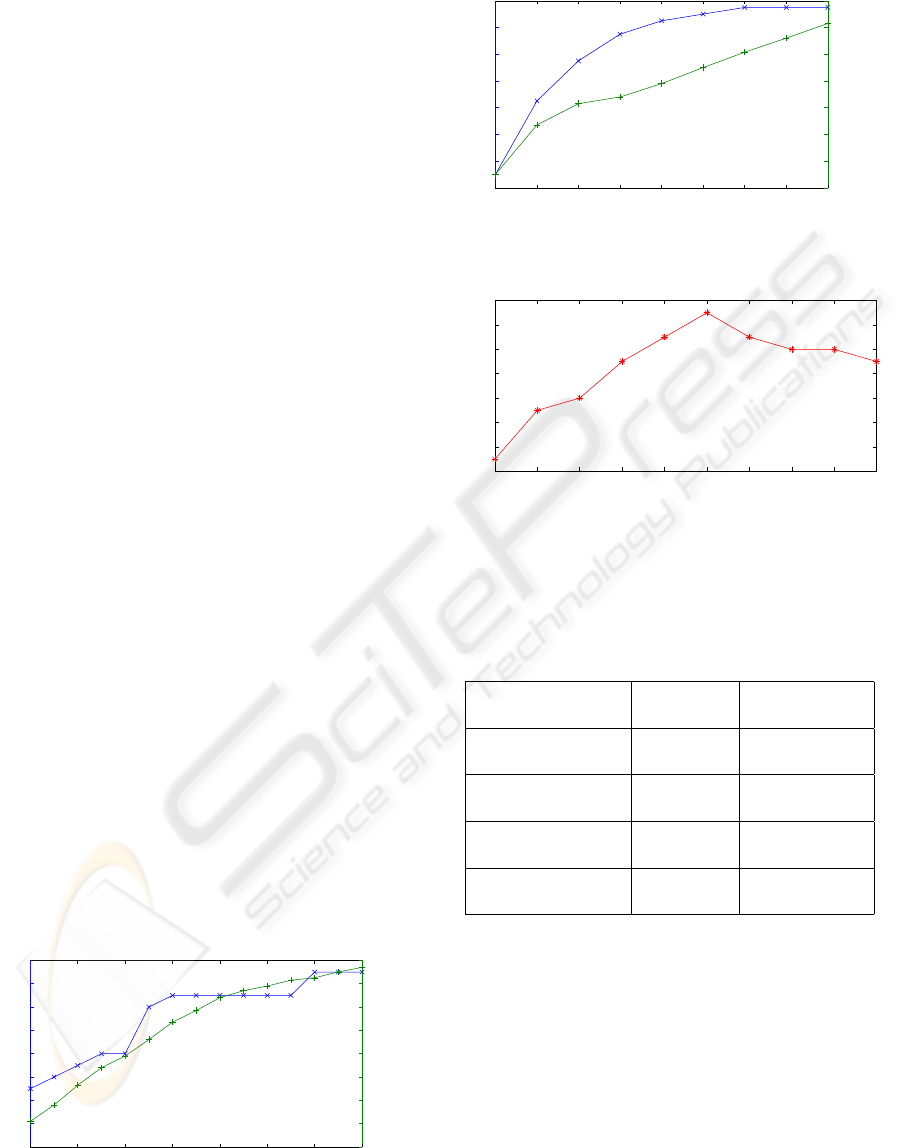
of edge-segments N. In ﬁgure 5 the accurateness of

the segmentations and the runtime are plotted against

N. While runtime increases continuously with just a

slight decrease towards higher values of N, accurate-

ness increases more sharply and then ﬂattens. Choos-

ing a high accurateness per runtime suggest 160 as a

good value for N.

The Level of Connectivity of the Graph Edges.

the degree to which the graph is connected as ex-

plained in 6 the limit of nodes per vertex V is plot-

ted against accurateness of the segmentations and the

runtime. Again runtime increases continuously with

V, while accurateness increases more sharply and then

ﬂattens out. The best accurateness per runtime ratio

is reached at values of 4 and 5, however to boost ac-

curateness a value of 7 is chosen as the default value

for subsequent experiments.

Cost Function. Figure 7 plots the segmentation ac-

curateness against α. As expected, accurateness ini-

tially rises with α as the values of VLL in the out-

put contour are reduced to a minimum to reﬂect the

grouping phenomenon of proximity. After α = 3.5 the

amount of good segmentations starts declining. This

value is thus a good choice which minimizes VLL and

yet still allows edge-segments with high prominence

to inﬂuence the result.

A Priori Knowledge. One of the stated aims of this

work is to present a segmentation method that allows

the integration of a priori knowledge of the object to

100 120 140 160 180 200 220 240

Number of edges

Accurateness − Number of good segmentations

100 120 140 160 180 200 220 240

120

140

160

180

200

220

240

260

280

Runtime (ms)

Figure 5: Number of good segmentation results and runtime

against N.

1 2 3 4 5 6 7 8 9

Number of vertices

Accurateness − Number of good segmentations

1 2 3 4 5 6 7 8 9

100

140

180

220

260

300

340

Runtime (ms)

Figure 6: Amount of good segmentations and runtime

against maximum successor constraint.

1 1.5 2 2.5 3 3.5 4 4.5 5 5.5

alpha

Number of good segmentations

Figure 7: Amount of good segmentations against α.

be segmented. To demonstrate the impact of a priori

knowledge of the object shape, simulated data at two

different resolutions is used as explained in 4.1. In the

Table 1: Segmentation with different A Priori Knowledge.

Shape Good Seg- Runtime

Knowledge mentations

low res - reduction 29 6.7s

of search space (58%) (134ms/Frame)

high res - reduction 38 5.5s

of search space (76%) (110ms/Frame)

high res - no reduc- 31 15.5s

tion of search space (62%) (310ms/Frame)

none 27 13.0s

(54%) (260ms/Frame)

ﬁrst two tests both an increase of prominence values

and a reduction of the search space was performed.

As can be seen in Table 1 this results in a higher num-

ber of good segmentations and a reduced runtime.

Both improvements are stronger in the case of

higher resolution shape knowledge. In the third test,

only the prominence values are increased, but the

search space is not reduced. Hence, the results show

no improvement in runtime. More good segmenta-

tions are achieved than without shape knowledge, but

less as with search space reduction. In the interests

of obtaining good segmentations in short time, it is

recommended to reduce the search space to pixels in

SEGMENTATION THROUGH EDGE-LINKING - Segmentation for Video-based Driver Assistance Systems

the boundary region. Shape knowledge may help with

some problematic cases, like the pedestrian depicted

in Figure 8, which is cut in half due to a strong edge

at the waist.

Figure 8: Selected segmentations. Left: without shape

knowledge, Center: with higher resolution shape knowl-

edge, Right: shape masks.

4.3 Comparison with GVF Snakes

Gradient Vector Field (GVF) (Xu and Prince, 1998)

represent a well-known method with scope for us-

ing a priori knowledge of the object thus providing

a good comparison for the method proposed in this

work. The tests were conducted with a reference Mat-

lab implementation provided by the authors (Xu and

Prince, 1998) using the following parameter values:

α = 1, β = 0 and µ = 0.2. The ROIs of the proposed

method are used as initial points. With GVF Snakes,

18 (36%) good segmentations are obtained, compared

to 27 (54%) with the proposed method. In Figure 9

some segmentation results of the proposed method are

compared to segmentations from GVF Snakes. The

white boxes are the initial ROIs. In the upper left case

both methods are successful. At the bottom of the car

Figure 9: Comparison of the proposed method with GVF

Snakes. ROIs used are depicted as white boxes.

GVF Snakes perform better, since the internal forces

of the algorithm try to stick to the strong edge directly

underneath the car. However, in the other two cases

this property is problematic, since the contour there

sticks to strong edges on the background an inside the

object. In the case of the pedestrian, there are prob-

lems entering the concavities.

5 CONCLUSIONS

This work presents an approach to object-

segmentation based on the grouping of edge-

segments. In comparison with previous approaches it

introduces the following new processing steps:

Detection of weak and strong edges by increasing

edge detection thresholds provides a fast method

for ranking the prominence of detected edge pixels.

Improvement of the generation of edge-segments

by splitting at points of high curvature allows more

grouping permutations. Introduction of a new

cost-function, which allows for a trade off between

the average edge-segment prominence and edge

gap length VLL. Use of a priori knowledge to boost

segmentation results and concurrently allow for

shorter running time.

Because the closed contours are formed from edge

pixels detected by the Canny edge detector, the results

show good edge localization. The proposed method

yields better results within the problem domain of

automotive applications, than the use of GVF Snakes.

Those show more problems with background and

internal edges as well as with object concavities.

The following points outline possible directions for

further work on this topic:

Improving Contour Selection: This work also

introduces a new way to select object hypothesis

based on a formula considering both high area and

low cost. It is conceivable however, that a more

sophisticated method could be applied. It could be

either model-free as in our case or incorporation

speciﬁc knowledge of the target objects’s shape.

Using Previous Video Frames: If the method is to be

applied on video sequences, the output of a previous

frame could be used as a priori shape knowledge for

the next frame. In this case a combination and / or

comparison with motion segmentation approaches

would also be of interest.

Using Color: If colored images are available, more

salient edges could be generated with a color-edge

detector. With those, the algorithm, which would

largely remain the same, may yield better results.

IMAGAPP 2009 - International Conference on Imaging Theory and Applications

ACKNOWLEDGEMENTS

The authors would like to thank S.Kiranyaz et al. for

providing practical information about their method.

REFERENCES

Canny, J. (1986). A computational approach to edge de-

tection. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 8(6):679–698.

Elder, J. H. and Zucker, S. W. (1996). Computing Contour

Closure. In ECCV ’96: Proceedings of the 4th Euro-

pean Conference on Computer Vision-Volume I, pages

399–412, London, UK. Springer-Verlag.

Fawcett, T. (2004). ROC Graphs: Notes and Practical Con-

siderations for Researchers. Machine Learning, 31.

Gonzalez, R. and Woods, R. (1987). Digital image process-

ing. Addison-Wesley Reading, Mass.

Kiranyaz, S., Ferreira, M., and Gabbouj, M. (2006). Auto-

matic Object Extraction over Multi-Scale Edge Field

for Multimedia Retrieval. IEEE Transactions on Im-

age Processing, 15(12):3759–3772.

Lowe, D. G. (1985). Perceptual Organization and Visual

Recognition. Kluwer Academic Publishers, Norwell,

MA, USA.

Mahamud, S., Williams, L., Thornber, K., and Xu, K.

(2003). Segmentation of multiple salient closed con-

tours from real images. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 25(4):433–444.

Stahl, J. and Wang, S. (Oct. 2007). Edge Grouping Com-

bining Boundary and Region Information. Image Pro-

cessing, IEEE Transactions on, 16(10):2590–2606.

Wang, S., Kubota, T., Siskind, J. M., and Wang, J. (2005).

Salient Closed Boundary Extraction with Ratio Con-

tour. IEEE Transactions on Pattern Analysis and Ma-

chine Intelligence, 27(4):546–561.

Xu, C. and Prince, J. (1998). Snakes, shapes, and gradient

vector ﬂow. Image Processing, IEEE Transactions on,

7(3):359–369.

SEGMENTATION THROUGH EDGE-LINKING - Segmentation for Video-based Driver Assistance Systems