THE PULL-PUSH ALGORITHM REVISITED

Improvements, Computation of Point Densities, and GPU Implementation

Martin Kraus

Computer Graphics & Visualization Group, Technische Universit¨at M¨unchen, Boltzmannstraße 3, 85748 Garching, Germany

Keywords:

Pyramid algorithm, Image processing, Real-time rendering, Scattered data, Meshless data, Interpolation, GPU.

Abstract:

The pull-push algorithm is a well-known and very efﬁcient pyramid algorithm for the interpolation of scattered

data with many applications in computer graphics. However, the original algorithm is not very well suited for

an implementation on GPUs (graphics processing units). In this work, several improvements of the algorithm

are presented to overcome this limitation, and important details of the algorithm are clariﬁed, in particular the

importance of the correct normalization of the employed ﬁlters. Moreover, we present an extension for a very

efﬁcient estimate of the local density of sample points.

1 INTRODUCTION

Interpolation of scattered data points is a classi-

cal problem in computer graphics with many appli-

cations, e.g., inpainting, reconstruction of smooth

functions from meshless point data, image post-

processing effects, etc. (Gortler et al., 1996; Drori

et al., 2003). As recent GPU implementations of

pyramid algorithms for scattered data interpolation

achieve real-time performances, they are also suited

for real-time rendering and real-time video processing

(Lefebvre et al., 2005; Strengert et al., 2006; Guen-

nebaud et al., 2007; Kraus and Strengert, 2007a).

However, there are particularly challenging ren-

dering algorithms, which require the interpolation of

scattered pixels for multiple images per frame. For

example, the rendering of depth-of-ﬁeld effects by

Kraus and Strengert (Kraus and Strengert, 2007a) re-

quires two full-screen interpolation passes for each

“subimage” with 1 to 20 “subimages” per frame (de-

pending on the strength of the effect). Thus, even

a high-performance GPU implementation of scat-

tered data interpolation can constitute a serious per-

formance bottleneck for some rendering algorithms.

Therefore, this work is concerned with improvements

of GPU implementations of the very efﬁcient pull-

push algorithm by Gortler et al. (Gortler et al., 1996).

The next section brieﬂy summarizes related work

while Section 3 presents our algorithmic improve-

ments of the pull-push algorithm and compares them

to the original algorithm. Section 4 presents a variant

of the algorithm to compute the local density of sam-

ple points, and in Section 5, the GPU implementations

of the algorithms and their performance is discussed.

2 RELATED WORK

The original pull-push algorithm by Gortler et al.

(Gortler et al., 1996) is based on work by Burt (Burt,

1981; Burt, 1988) and Mitchell (Mitchell, 1987)

and was used to interpolate between many sampling

points in a four-dimensionaldomain in the Lumigraph

system.

A variant of the pull-push algorithm was em-

ployed, for example, by Drori et al. (Drori et al.,

2003) for an initial reconstruction of missing parts

of images. Lefebvre et al. (Lefebvre et al., 2005)

used a GPU-based implementation for inpainting

gaps in texture maps. Strengert et al. (Strengert et al.,

2006) proposed a more efﬁcient GPU implementa-

tion, which is of linear time complexity in the number

of pixels. The algorithm by Strengert et al. was em-

ployed by Kraus and Strengert (Kraus and Strengert,

2007a) to disocclude pixels in their depth-of-ﬁeld al-

gorithm. Guennebaud et al. (Guennebaud et al., 2007)

employed a GPU implementation of the pull-push al-

gorithm to reconstruct soft shadows from a reduced

number of sample points; however, they did not de-

scribe any details of their implementation.

179

Kraus M. (2009).

THE PULL-PUSH ALGORITHM REVISITED - Improvements, Computation of Point Densities, and GPU Implementation.

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 179-184

DOI: 10.5220/0001772601790184

 SciTePress

n−1

...

n−2

−1

...

n−1

−2

n−1

−1

...

−4

−3

−2

−1

Figure 1: Illustration of the pixels x

of an image pyramid

for a one-dimensional input image x

of size 2

3 REVISION OF THE PULL-PUSH

ALGORITHM

3.1 Pull

The original pull phase by Gortler et al. (Gortler et al.,

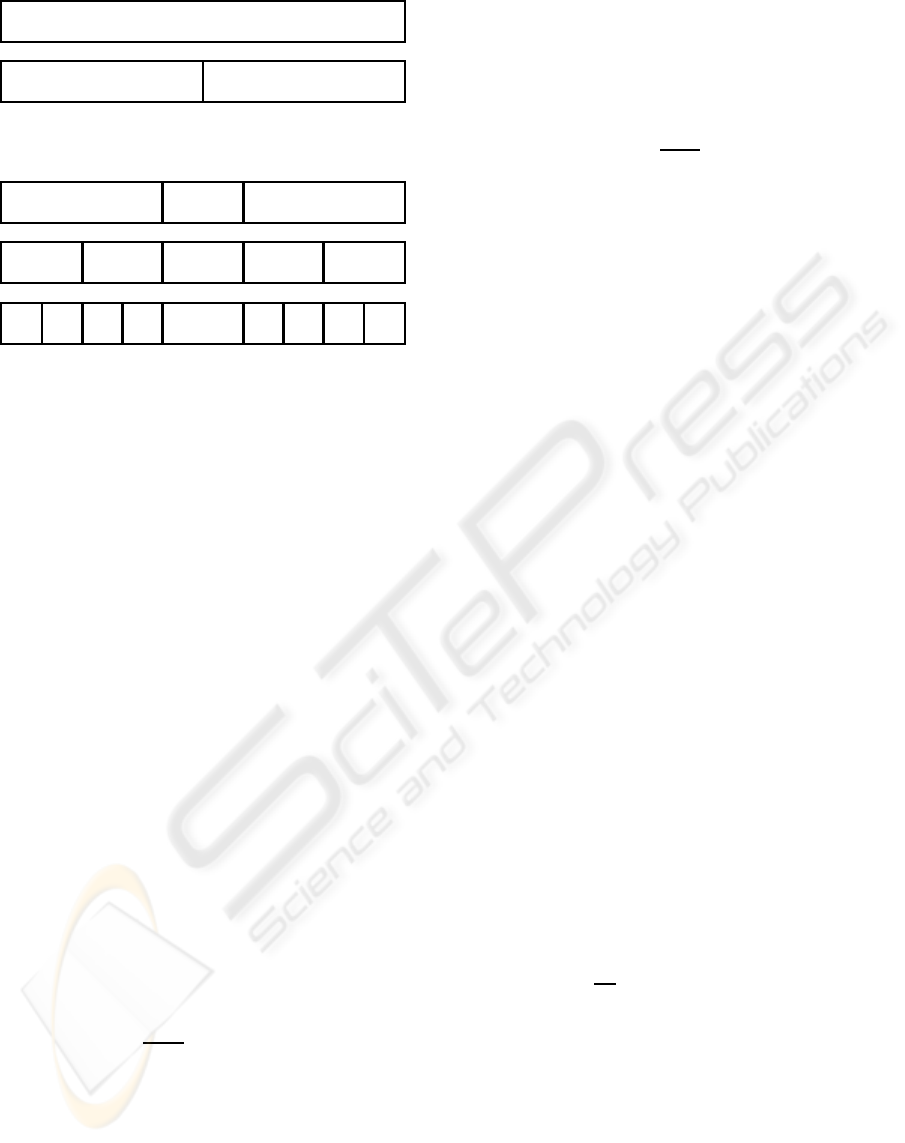
1996) computes an image pyramid of data values x

and positive weights w using a “pull ﬁlter”

h. The

input image determines the size of the ﬁnest pyramid

level r = 0 while the size of pyramid level r+1 is half

of the size of pyramid level r in each dimension. For

clarity we describe the algorithm for one-dimensional

images and restrict their sizes to powers of two. Data

values of pyramid level r are denoted by x

and their

weights by w

where r equals 0 for the original (ﬁnest)

resolution and pixels are indexed by i. This structure

of a one-dimensional image pyramid is illustrated in

Figure 1.

If the pull ﬁlter is speciﬁed by a discrete sequence

h of positive numbers, Gortler et al. suggest to com-

pute the pixels of the next coarser image level by:

r+1

∑

k−2i

min(w

, 1) (1)

r+1

∑

k−2i

min(w

, 1)x

(2)

To reduce the number of clamp operations, i.e., min

functions, we propose to introduce clamped weights

ˆw

and weighted data values ˜x

, in particular for the

input data on level r = 0:

ˆw

def

= min



, 1



, ˜x

def

= ˆw

(3)

The computation of coarser image levels can now be

performed with just one clamp operation and basic

ﬁlter operations:

r+1

∑

k−2i

ˆw

(4)

ˆw

r+1

= min



r+1

, 1



(5)

˜x

r+1

ˆw

r+1

∑

k−2i

˜x

(6)

This formulation is more suited for an efﬁcient GPU

implementation as discussed in Section 5.

It should be noted that the normalization of

h is

crucial for the quality of the resulting interpolation.

As shown in Section 3.3, a normalization of the max-

imum to 1 provides good results in most cases while

a normalization of the integral of the ﬁlter

h to 1 leads

to signiﬁcantly worse results.

Our new formulation encapsulates the nonlinear

part of the pull phase in a single clamp operation in

Equation 5, which can be replaced easily by a contin-

uous operation. For example, one could use a ﬁlter

h with a normalization such that its integral is 1 and

achieve an effect similar to the nonlinear clamp oper-

ation by employing the following equation instead of

Equation 5:

ˆw

r+1

= 1−



1− w

r+1



(7)

Here, γ is a parameter that controls the range of inﬂu-

ence of data points: larger values of γ tend to result in

larger regions around isolated data points where the

interpolated values are close to the values speciﬁed

for the data points; examples are given in Section 3.3.

3.2 Push

After the image pyramid has been computed, a se-

quence of push operations recomputes all levels from

coarse to ﬁne with a “push ﬁlter” h. First, two tempo-

rary values are computed:

∑

i−2k

min



r+1

, 1



(8)

∑

i−2k

min



r+1

, 1



r+1

(9)

Note that Gortler et al. use the symbol tw instead of ω

and tx instead of χ.

These temporary values are blended with the pre-

viously computed pyramid image. However, the

equations provided by Gortler et al. lack clamping op-

erations; the corrected equations are:

= χ

(1− min(w

, 1)) + min(w

, 1)x

(10)

= min(ω

, 1)(1− min(w

, 1))

+min(w

, 1) (11)

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

180

50 100 150 200 250

0.2

0.4

0.6

0.8

(a)

50 100 150 200 250

0.2

0.4

0.6

0.8

(b)

50 100 150 200 250

0.2

0.4

0.6

0.8

(c)

Figure 2: (a) Interpolation of a set of scattered data (gray bars) by the “original” algorithm by Gortler et al. (Gortler et al.,

1996) with

h =



, 1, 1,



(solid line) and

h =





(dashed line). (b) Interpolation by the “w/o clamp” algorithm

for γ = 4 (solid line) and γ = 16 (dashed line). For comparison, the result of the original algorithm is also included (dotted

line). (c) Same as (b) for input data of weight

instead of 1.

These equations can also be simpliﬁed by employing

clamped weights ˆw

and weighted data values ˜x

as in-

troduced in the previous section. For the push phase

we can additionally assume a normalization of the

push ﬁlter h such that no further clamp operations are

necessary. Therefore, Equations 8–11 can be rewrit-

ten as:

∑

i−2k

ˆw

r+1

(12)

∑

i−2k

˜x

r+1

(13)

= χ

(1− ˆw

) + ˜x

(14)

ˆw

(1− ˆw

) + ˆw

(15)

˜x

= ˆw

(16)

These ﬁlter operations can be implemented very ef-

ﬁciently (see Section 5); however, the linear inter-

polation with weights ˆw

and 1 − ˆw

cannot be im-

plemented by standard blending on GPUs due to the

multiplication in Equation 16.

Fortunately, these equations can be further simpli-

ﬁed by a new approximation, which works very well

for most input data and ﬁlters

h and h. As noted

above, the pull ﬁlter

h should be scaled such that

the weights ˆw

quickly approach 1 in coarser pyra-

mid levels. During the push phase these weights are

further increased, thus, they are usually equal to 1 or

close to 1 in all pyramid levels. This motivates a vari-

ation of the blending such that all new weights ˆw

are

(implicitly) set to 1. Thus, Equations 12–16 are sig-

niﬁcantly simpliﬁed to only two equations:

∑

i−2k

r+1

(17)

= χ

(1− ˆw

) + ˜x

(18)

Note that we start with x

r+1

instead of ˜x

r+1

on the

coarsest level, which can be easily computed in the

last step of the pull phase by avoiding the multiplica-

tion with ˆw

r+1

in Equation 6. For all but the ﬁrst iter-

ation, x

r+1

in Equation 17 refers to the pyramid level

that was most recently computed according to Equa-

tion 18 in the push phase, while ˆw

and ˜x

in Equa-

tion 18 refer to values computed in the pull phase.

Our new formulation allows for both an efﬁcient

GPU implementation of the ﬁltering operations by

texture ﬁltering as well as an efﬁcient GPU imple-

mentation of the linear interpolation by frame buffer

blending as discussed in Section 5.

3.3 Comparison of Variants

In this section, we compare the original algorithm by

Gortler et al. (Gortler et al., 1996) with the two vari-

ants proposed in Sections 3.1 and 3.2.

3.3.1 “Original” Algorithm

For the purpose of this comparison, the “original” al-

gorithm is described by Equations 3–6 for the pull

phase and Equations 8–11 for the push phase. A

one-dimensional pull ﬁlter

h is used, which is de-

ﬁned by the sequence



, 1, 1,



, i.e., the maximum

is normalized to 1. The push ﬁlter h is deﬁned by





. These ﬁlters correspond to quadratic B-

spline ﬁlters (Catmull and Clark, 1978) and are par-

ticularly well suited for GPU implementations (Kraus

and Strengert, 2007b).

Figure 2a depicts a set of scattered input pixels

of weight 1 in a one-dimensional image of dimen-

sion 256 and the data interpolation computed with

the original algorithm by Gortler et al. as described

above. For comparison, the results with a differently

normalized pull ﬁlter

h speciﬁed by





, is

also included. With input weights less than or equal to

1, this normalization guarantees that all weights stay

less than or are equal to 1 in the pull phase, therefore,

the clamp operations are unnecessary.

However, the latter pull ﬁlter does not provide a

smooth interpolation of the input points. In fact, it ap-

pears to be extremely difﬁcult—if not impossible—to

THE PULL-PUSH ALGORITHM REVISITED - Improvements, Computation of Point Densities, and GPU Implementation

181

(a) (b) (c)

Figure 3: (a) A two-dimensional image of size 256× 256. (b) Masked variant of the image in (a): the weight of black pixels

is 0, the weight of all others is 1. (c) Density of the pixels with weight 1 computed by the algorithm presented in Section 4.

(a) (b) (c)

Figure 4: Images reconstructed from Figure 3b using (a) the “original” algorithm, (b) the “w/o clamp” variant, (c) the “w/o

weight” variant.

design appropriate pull ﬁlters for the original algo-

rithm that do not require clamping operations but still

result in smooth interpolations. Thus, in contrast to

the discussion by Gortler et al., the clamping is not

only necessary to limit the inﬂuence of clusters of

many input points but it is also crucial for a smooth

interpolation in general.

3.3.2 Variant “w/o clamp”

In order avoid the nondifferentiable clamping and

to simplify the design of pull ﬁlters, we propose

a ﬁrst variant of Gortler et al.’s algorithm, named

“w/o clamp,” which replaces the clamping speciﬁed

in Equation 5 by the differentiable Equation 7. For

this variant of the algorithm, the integral of the pull

ﬁlter

h has to be normalized to 1 in order to guarantee

that weights do not exceed 1. We choose





for the examples depicted in Figure 2b and 2c. The

parameter γ in Equation 7 was set to 4 and 16 in order

to show its inﬂuence.

While the input pixels in Figure 2b are the same

as in Figure 2a, the input weights in Figure 2c are

only

instead of 1 in Figure 2b. The dotted curve

depicted in Figure 2c suggests that it is difﬁcult to ob-

tain a smooth curve approximating sample points with

weights less than 1 using the original algorithm. The

situation is quite similar to an unsuitable normaliza-

tion of

h as the clamping operation is ineffective for

several levels in both cases. On the other hand, al-

ternative nonlinear ﬁlters such as implemented in our

variant “w/o clamp,” can provide smoother curves for

input points with weights less than 1 as illustrated by

the dashed curve in Figure 2c.

3.3.3 Variant “w/o weight”

The second variant is named “w/o weight” and imple-

ments Equations 3–6 for the pull phase; however, the

multiplication with ˆw

r+1

in Equation 6 is skipped for

the coarsest level in order to compute x

r+1

instead of

˜x

r+1

. For the push phase, Equations 17 and 18 are

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

182

employed. In our experiments, this variant and the

original algorithm computed very similar results al-

though the “w/o weight” variant employs a consider-

ably simpliﬁed push phase, which is better suited for

an efﬁcient implementation on GPUs.

3.3.4 Two-Dimensional Examples

Figure 4 presents the two-dimensional results for the

input depicted in Figure 3b. Visually there are no dif-

ferences between the result of the original algorithm

employed for Figure 4a and the results for the two

new variants of the algorithm shown in Figure 4b and

Figure 4c.

4 COMPUTATION OF POINT

DENSITIES

It is often useful to compute a local density of scat-

tered points, for example in order to decide where to

place additional sampling points. Here we present a

computation of the local density of input points by a

variant of the presented pull-push algorithm.

We assume that all weights of input pixels w

are

equal to 1 and all weights of unspeciﬁed pixels are

0. In this case, the pyramid images w

computed in

the pull phase are in fact approximations of the den-

sity of input points if the integral of the pull ﬁlter

is normalized to 1. However, it is crucial to choose

an appropriate pyramid level r. In particular, r should

be chosen locally. To this end, we base the computa-

tion of the point density on those values w

where r

is appropriate for the speciﬁc position i. This can be

achieved by introducing new weights p

for the inter-

polation of densities w

: the weight p

determines the

inﬂuence of w

analogously to the role w

played for

in the original pull-push algorithm.

We determine actual values for p

in dependency

of the average number ¯n

of input points at pixel i in

the pyramid image at level r:

¯n

def

= 2

(19)

If the average number of input points per pixel ¯n

less than 1, p

should be 0 because the correspond-

ing w

is very likely to overestimate the local density

in the neighborhood of a single, isolated input point.

On the other hand, if ¯n

is very large, p

should also

be 0 as local variations of the density of input points

are not reﬂected by the corresponding w

if too many

input points are included in the average. In between

these extremes, p

is set according to a function p( ¯n),

which is application-speciﬁc as even very ﬁne local

2 4 6 8

0.2

0.4

0.6

0.8

pHnL

Figure 5: Two examples for the function p(n) to deter-

mine weights depending on the average number n of in-

put points per pixel. The solid curve is suitable for one-

dimensional images while the dotted curve is suitable for

two-dimensional images.

variations are of interest in some cases—for exam-

ple when estimating the distance to the nearest in-

put point—while other applications—in particular for

high-dimensional images—require larger values of ¯n

to reliably estimate the density of input points. Fig-

ure 5 illustrates two examples for the function p( ¯n).

Having computed densities w

and their weights

in the pull phase, we can then apply a push phase,

which reconstructs a smooth function for w

on the

ﬁnest pyramid level analogously to reconstructing a

smooth function x

from data values x

and weights

. Next we describe this algorithm for the GPU-

friendly variant of the pull-push algorithm presented

in Section 3.2 (called “w/o weight” in Section 3.3).

The algorithm starts with an input image w

where the w

’s are either 0 or 1. The pull phase im-

plements the following equations:

r+1

∑

k−2i

(20)

¯n

r+1

= 2

r+1

(21)

r+1

= p



¯n

r+1



(22)

As mentioned above, the integral of the pull ﬁlter

has to be normalized to 1. The push ﬁlter h has to be

normalized analogously and is used in the push phase,

which recomputes the image pyramid from coarse to

ﬁne levels using these equations:

∑

i−2k

r+1

(23)

= χ

(1− p

) + p

(24)

The ﬁnest pyramid image w

is the resulting estimate

of the local density of points.

Figure 3c depicts the resulting density for the in-

put shown in Figure 3b. The two-dimensional gener-

alizations of the same pull and push ﬁlters were em-

ployed and the dotted curve in Figure 5 was used for

p( ¯n).

THE PULL-PUSH ALGORITHM REVISITED - Improvements, Computation of Point Densities, and GPU Implementation

183

5 GPU IMPLEMENTATION

While there are very efﬁcient GPU implementations

of linear ﬁltering (Kraus and Strengert, 2007b), any

additional functions in the summation (as in Equa-

tion 1) or additional nonconstant factors (as in Equa-

tion 2) defeat an efﬁcient GPU implementation. This

problem is solved by our improvements presented in

Section 3, in particular Equations 4, 6, and 17.

For multidimensional data (e.g., RGB images) the

ﬁltering operations in Equations 6 and 17 can be per-

formed in parallel for up to 3 components on GPUs.

Moreover, the ﬁltering of weights in Equation 4 can

be performed in parallel in the A component of an

RGBA texture image in order to implement Equa-

tion 18 by alpha-blending. Note that only ˆw

and ˜x

have to be stored in the pull phase, while the push

phase only stores new values for x

in place of the

values ˜x

, which were computed in the pull phase.

While Gortler et al. (Gortler et al., 1996) claim

that Equations 8–11 can be implemented by standard

blending, this is unfortunately no longer true if the

computation is based on weighted variables ˜x

for

more efﬁcient ﬁltering. This problem is solved by the

approximation presented in Section 3.2, in particular

Equations 17 and 18.

The two-dimensional ﬁlters employed in Sec-

tion 3.3 require only four texture lookups per pixel

of the coarser level in the pull phase and one texture

lookup per pixel of the ﬁner level in the push phase

if the ﬁltering is implemented efﬁciently (Kraus and

Strengert, 2007b). As GPU implementations of the

proposed algorithms are bandwidth-limited, the arith-

metic operations do not signiﬁcantly affect the per-

formance. Our implementation requires 0.60 ms for a

1024 × 1024 16-bit ﬂoating-point RGBA image on a

NVIDIA Quadro FX 5800 graphics board.

6 CONCLUSIONS

As shown in this work, the proposed algorithms for

the interpolation of scattered data points and the com-

putation of local densities of scattered points are well

suited for very efﬁcient GPU implementations, which

could be used for real-time rendering or real-time im-

age and video processing.

The quality of the results computed by the pro-

posed algorithms depends on the choice of the pull

and push ﬁlters, the nonlinear function in Equation 7,

and the function p( ¯n) in Equation 22. Determining

suitable ﬁlters and functions for particular applica-

tions is part of future work.

REFERENCES

Burt, P. J. (1981). Fast Filter Transforms for Image Pro-

cessing. Computer Graphics and Image Processing,

16:20–51.

Burt, P. J. (1988). Moment images, polynomial ﬁt ﬁlters,

and the problem of surface interpolation. In Pro-

ceedings of Computer Vision and Pattern Recognition,

pages 144–152.

Catmull, E. and Clark, J. (1978). Recursively Generated

B-Spline Surfaces on Arbitrary Topological Meshes.

Computer Aided Design, 10(6):350–355.

Drori, I., Cohen-Or, D., and Yeshurun, H. (2003).

Fragment-Based Image Completion. ACM Transac-

tions on Graphics, 22(3):303–312.

Gortler, S. J., Grzeszczuk, R., Szeliski, R., and Cohen, M. F.

(1996). The Lumigraph. In SIGGRAPH ’96: Pro-

ceedings of the 23rd Annual Conference on Computer

Graphics and Interactive Techniques, pages 43–54.

Guennebaud, G., Barthe, L., and Paulin, M. (2007). High-

Quality Adaptive Soft Shadow Mapping. Computer

Graphics forum (Proceedings Eurographics 2007),

26(3):525–533.

Kraus, M. and Strengert, M. (2007a). Depth-of-Field Ren-

dering by Pyramidal Image Processing. Computer

Graphics Forum (Conference Issue), 26(3):645–654.

Kraus, M. and Strengert, M. (2007b). Pyramid Filters Based

on Bilinear Interpolation. In Proceedings GRAPP

2007 (Volume GM/R), pages 21–28.

Lefebvre, S., Hornus, S., and Neyret, F. (2005). Octree Tex-

tures on the GPU. In Pharr, M., editor, GPU Gems 2,

pages 595–613.

Mitchell, D. P. (1987). Generating Antialiased Images at

Low Sampling Densities. In Proceedings of SIG-

GRAPH ’87, pages 65–72.

Strengert, M., Kraus, M., and Ertl, T. (2006). Pyramid

Methods in GPU-Based Image Processing. In Pro-

ceedings Vision, Modeling, and Visualization 2006,

pages 169–176.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

184