
CLASSIFIERS SENSITIVITY FOR BOUNDARY CASE TESTING
SET IN THE FACE RECOGNITION ALGORITHM BASED ON
THE ACTIVE SHAPE MODEL
Andrzej Florek and Maciej Król
Institute of Control and Information Engineering, Automatic Control and Robotics Division
Poznan University of Technology, str. Piotrowo 3A, 60-965 Poznań, Poland
Keywords: Face recognition, Active Shape Model, Principal Component Analysis, Linear Discriminant Analysis,
Support Vector Machine and Classification.
Abstract: In this paper, experimental results from the face contour classification tests are shown. The presented
approach is dedicated to a face recognition algorithm based on the Active Shape Model method. The results
were obtained from experiments carried out on the set of 3300 images taken from 100 persons.
Automatically fitted contours (as 194 ordered face contour points vector, where the contour consisted of
eight components) were classified by Nearest Neighbourhood Classifier and Support Vector Machines
classifier, after feature space decomposition, carried out by the Linear Discriminant Analysis method.
Feature subspace size reduction and classification sensitivity analysis for boundary case testing set are
presented.
1 INTRODUCTION
In this paper, a discussion concerning the choice of
a classifier for the face recognition algorithm is
presented. We investigate how the classification
sensitivity coefficient is influenced by: the feature
vector size, the size of the Principal Component
Analysis (PCA) used for contours validation
procedure, the size of the Linear Discriminant
Analysis (LDA), number of classes and boundary
case testing set. The presented algorithm for face
classification is based on the Active Shape Model
method (ASM) introduced by Cootes (Cootes and
Taylor, 2001), which is a modification of the Active
Contour Model method (ACM), i.e. a snake-based
approach to extracting face contour from an image
(Kass and Witkin, 1988). The ASM is a two-stage
algorithm and it is based on a shape notation, which
is defined as an ordered set of points. First, a Point
Distribution Model (PDM) is produced, which will
be used for validation of a contour shape. Next,
a Local Grey Level Model (LGLM) is generated for
interactive fitting of the contour points to the local
image context. This method is still in progress,
where modifications consist of initial contour choice
and the new fitting methods (Zao and Li, 2004),
(Zuo and de With, 2004). The ASM has been
successfully used to extract the facial features of
a face image under frontal view. However, its
performance degrades when the concerned face is
under perspective variations. For this reason,
a modified shape model was proposed by Wan and
Lam (Wan and Lam, 2005). It can adapt face images
from different orientations or facial expressions
and
represents a face more flexibly.
To obtain PDM and LGLM models, the desirable
contour localization on an image of a person has to
be known. Thus, placing contours onto images
(chosen to create a learning set) has to be performed
and this may be done manually or automatically.
Arrangement of proper learning set is usually the
most important problem of a good classifier choice.
A standard approach to classification consists of
determining an affiliation of a sample to a class
represented by its model. To construct a model of
a person, a set of images has to be produced. These
images have to be divided into learning and testing
sets, for example by simple sampling or multiple
sampling with replacement. The classification
improvement should be achieved by removing the
identified outliers from a training set. Generally, the
database is built under surveillance of specialists and
281
Florek A. and Krøsl M.
CLASSIFIERS SENSITIVITY FOR BOUNDARY CASE TESTING SET IN THE FACE RECOGNITION ALGORITHM BASED ON THE ACTIVE SHAPE MODEL.
DOI: 10.5220/0001772902810287
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications (VISIGRAPP 2009), page
ISBN: 978-989-8111-69-2
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

under determined conditions (distance, light,
position, etc.). In practical vision system, the picture
of a person (sample) is taken without this
surveillance and allows the person a freedom of pose
and gesture. Thus, the classification efficiency is in
practice lower than it was anticipated. This problem
can occur in the situation, when we want to verify if
a person from an accidental image is not wanted. In
the presented paper, we propose another testing set,
which is obtained from images of faces in extreme
positions
under different perspective variations and
facial expressions than in the conventional learning
set (boundary cases).
2 CONTOURS
The shape in the ASM method is represented as an
ordered set of control points placed on contours
describing face elements and it is given by the
following vector
x = ( x
1
, y
1
, x
2
, y
2
,..., x
n
, y
n
)
T
, (1)
where x
j
and y
j
are coordinates of contour control
points. In the considered case, for eight chosen
components of face contours, n = 194 points have
been determined (Fig. 1 and Tab.1) and this implies
388-dimensional shape space.
Table 1: Face contours.
Contou
r
Number of points
Face outline FO 41
Mouth outer MO 28
Mouth inner MI
28
Right eyelid REL 20
Left eyelid LEL 20
Right eyebrow REB 20
Left eyebrow LEB 20
Nose outline NO 17
TOTAL
194
2.1 Extracting and Calculation of
Contours
To obtain normalized learning contours, the initial
contour (template – Fig. 1) is placed on the image.
Next, it is manually fitted to the correct place that
the operator regards as the best localization for the
contour points. Subsequently, the derived contours
are normalized. Scale coefficient and rotation of
contour result from the calculated coordinates of eye
centres (pupils). Pupil coordinates are calculated
from coordinated contour points located in the eyelid
corners. Pupil coordinates determine X-axis; points
(-1, 0), (1, 0) are located on right and left pupil,
respectively. The symmetrical of this section
determines Y-axis and the middle of coordinate
system. Next, the contour points are projected on
a normalized coordinate system. The normalized
contour has to be uniformly sampled (manually
extracted contours do not have uniform distances
between the adjacent contour control points). The
normalized and uniformly sampled contours are
presented in Fig. 2.
Figure 1: Template contour.
During the normalization procedure, points are
ordered in a defined sequence, according to the
feature vector definition (1). In the presented
approach, the height standardization of face and
nose outlines has not been applied.
Figure 2: Normalized manually fitted contour.
3 EXPERIMENT
In order to select classifiers for the ASM face
recognition algorithm, an experiment consisting of
examining a set of face images was undertaken.
Colour images of 2048 × 1536 pixels were used. For
100 persons (100 classes) the following images were
taken (Fig. 11 and 12):
H – sequence of 30 frames for horizontal head
rotation from the right to the left half-profile;
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
282

V – sequence of 20 frames for vertical face rotation
from slightly risen to hang down head
position;
D – frames for different head positions and facial
expressions
(boundary cases).
The contours were manually positioned on 11
central succeeding images (frames) from H and V
sequences. In presented experiment, 2200 contours
were used as the manual learning set (LSM) for the
ASM algorithm (to determine PDM and LGLM
models). Next, the ASM algorithm was performed to
generate automatic contours for images from H and
V sequences and additionally from D-sequence.
3.1 Set Definitions
The normalized automatic contours were divided
into the following sets (see Fig. 11 and 12):
LSA – automatic learning set, 2200 contours,
100 classes, 22 contours for each class (11
central from H sequence and 11 central from V
sequence);
A – learning or testing set, 1100 contours, 100
classes, 11 contours for each class, even frames
subset of LSA;
B – learning or testing set, 1100 contours, 100
classes, 11 contours for each class, odd frames
subset of LSA;
C100 – testing set, 1100 automatic contours,
100 classes, 11 contours for each person from
H, V (boundary case in relation to LSA) and D.
The boundary case set C100 is almost a “regular
and balanced set”, i.e. consists of 4 contours from
both H and V sequences, (out of 11 central images)
and of 3 contours from D sequence. In the goal to
examine influence of number of classes on
classification sensitivity coefficient, the set C100
was also divided to subsets Cnc, where nc is the
number of classes, i.e. two C50, three C33, four C25
and five C20. From analogical reasons, the learning
set LSA was divided in the equivalent manner too.
Both A and B sets were used as learning or
testing sets alternatively. The normalized contours
from testing set C100 were slightly different for the
same person than those from learning sets (Fig. 3).
3.2 Contour fitting
The algorithm of contour fitting utilizes the ASM
method (Fig. 4). Firstly, Gaussian pyramid for input
image is generated. The initial contour shape is
placed at the coarsest level of the pyramid.
Secondly, the initial contour is initialised by placing
the mean face shape model (calculated from learning
Figure 3: Normalized contours: manual contours from the
learning set LSM (left column); automatic contours from
the testing set C100 (right column).
set LSM, see Fig. 1) at the position of localized face.
Two steps of the ASM algorithm (LGLM and PDM
– Fig. 4) are executed in a loop. The LGLM step
locates salient features of image along the normal
direction of contour control points. Each contour
point (x
i
, y
i
) is shifted along the normal to the best
matching position (x
ij
, y
ij
). The matching error is
defined as minimal Mahalonobis distance d
ij
()()
iiji
T
iijij
d
δδδδ
−−=
−1
C
(2)
from current LGL profile
δ
ij
to mean profile
⎯δ
i
for
a given contour control point. The mean
⎯δ
i
and
covariance C
i
are computed from local grey level
around manual contours control points (LSM) taken
from learning set of images.
In the PDM step, the shape is filtered with
forward (3) and inverse (4) transformations
()
xxb
T
−= P
(3)
bxx P+≈
(4)
to and from the subspace reduced by the PCA. The
transformation matrix P is selected as the first p-
CLASSIFIERS SENSITIVITY FOR BOUNDARY CASE TESTING SET IN THE FACE RECOGNITION ALGORITHM
BASED ON THE ACTIVE SHAPE MODEL
283
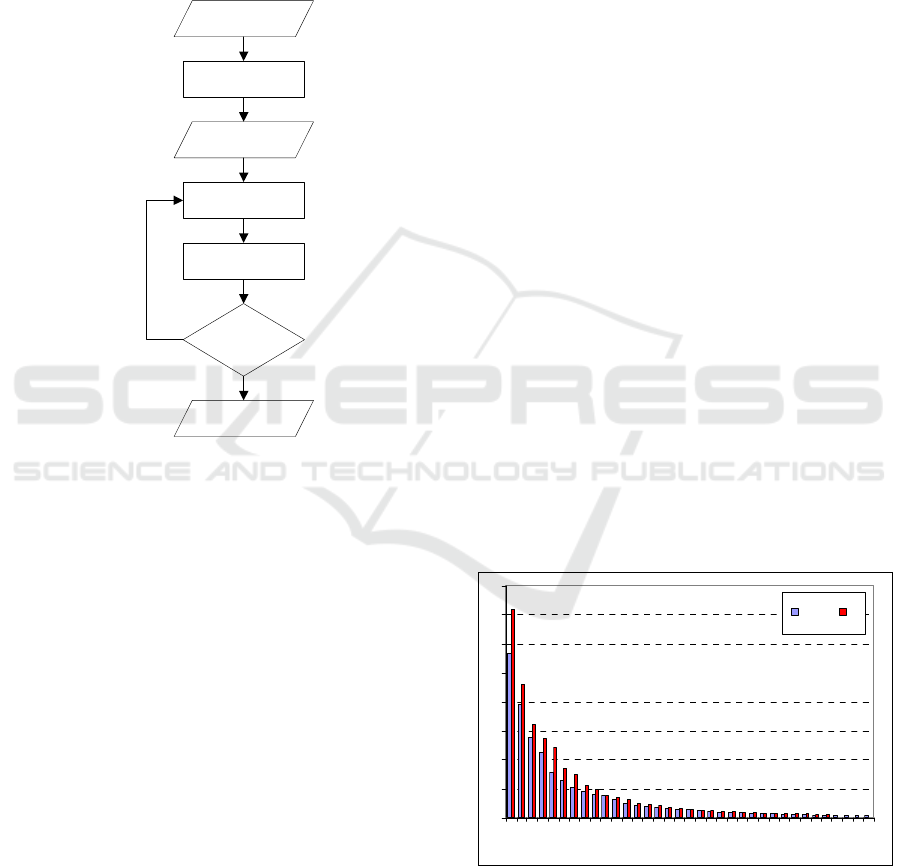
eigenvectors (p first PCs) of covariance matrix of
contours from learning set. In the presented paper,
value p=45 were used at 98,8% total variance ratio.
The choice of this size is very important because it
affects classification efficiency for applied classifier
(this will be discussed later in this paper). The
iteration ends when shapes stop changing
significantly and computation is repeated for finer
level of image pyramid until the last level is reached.
Figure 4: ASM algorithm diagram.
3.3 Classifiers
Three classification methods were tested. The first
classifier was the Nearest Neighbourhood Classifier
(NNC) in reduced to k-size feature shape subspace,
derived from LDA/k decomposition. As a metric,
Euclidean distance to a model of class in subspaces
for different size k was used (subspaces are not
orthogonal). The second method was taken as the
SVM method using a Radial Basis Function as
kernel and one-to-one voting system with a tie-
breaking algorithm. In the presented approach, SVM
classifiers were applied in full feature space and in
its k-subspaces (the third method), obtained after the
LDA/k decomposition in the feature space. As
sensitivity measure of classifiers (recognition rate)
the coefficient TP/(TP+FN) in percent was chosen,
where TP and FN are numbers of True Positive (the
person correctly recognized) and False Negative (the
person not properly recognized) classifications.
Classification methods are denoted as:
LDA/k – Euclidean distance in k-size
feature space reduced after Linear
Discriminant Analysis;
SVM – SVM classifier in full 388-
dimentional feature space;
LDA/k & SVM – SVM classifier in LDA
subspace reduced to k-size.
3.4 Choice of PCA Size for PDM
Validation
Determining the dimensionality of the PCA
subspace, i.e. the number of PCs to represent face
patterns (contours), is an intricate problem. It is
usually a trade
-off between estimation accuracy and
computational efficiency (Motulsky, 1997).
Calculated eigenvalues and cumulative variances are
presented in Fig. 5 and 6.
The reduction of the feature vector space to
around the first p=30 PCs seems to be reasonable
(97% of total data variance). Classification results
for learning set LSA (average from tests where A and
B sets were used as learning or testing sets
alternatively) are presented in Fig. 7 and confirm the
choice of first 30 PCs. However, results for
boundary case testing set C suggest that the
dimension size p= 45 (98,8% of total variance) will
be better for LDA classifier. Small vector size in the
PDM validation stage in the ASM algorithm unifies
contours and smoothes between-class differences.
Large vector size causes relaxation of contour and
reduces noise resistance. For the PDM validation
procedure in performed ASM algorithm, vector of
the first 45 PCs was chosen.
Figure 5: Eigenvalues in the PCA decomposition.
face image
face detection
LGL localization
PDM validation
shape
converged?
face shape
Yes
No
initial shape
0
1
2
3
4
5
6
7
8
1 6 11 16 21 26 31
Eigenvalue index p
LSA C
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
284
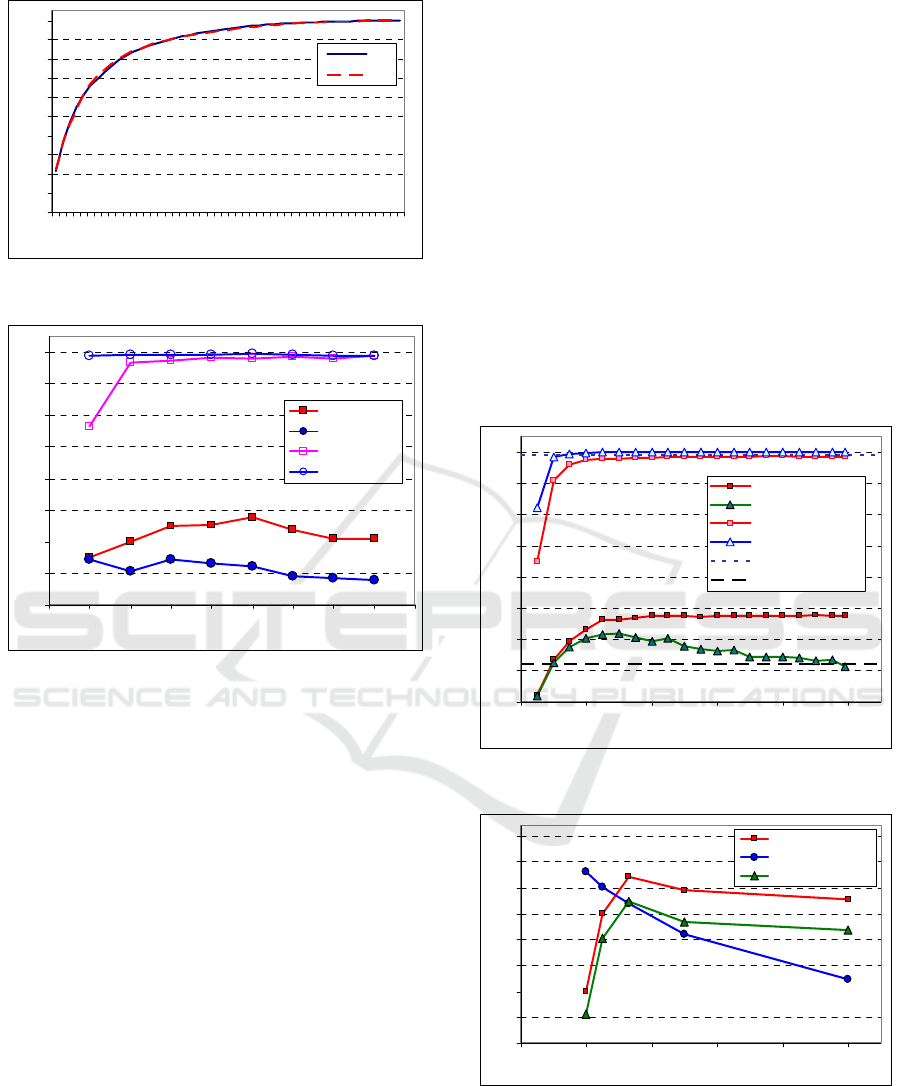
Figure 6: Cumulative variance in the PCA decomposition.
Figure 7: Classification sensitivity for LSA and C100 sets.
3.5 Results and Discussion
The SVM method is commonly used for
classification. As we can see in Fig. 7, this method is
good for testing samples similar to those from
learning set (i.e. when they are close with respect to
the face position and gestures). Classification
efficiency obtained from LSA set was equal (or very
close) to 100%. Experimental results demonstrate
good property of SVM classifier, however this is the
situation where the learning and testing sets were
regular subsets of larger learning set LSA. For the set
C as the testing set, the LDA classifier was much
better than the SVM classifier in full-dimensional
feature space. This suggests that the LDA method is
more resistant to diversity of a testing set, because
the space transformation function is found in order
to maximize the ratio of between-class variance to
within-class variance. In subsequent tests we
investigated influence of the proposed LDA
decomposition on amelioration of classification
sensitivity for boundary case set. Results are
presented in Fig. 8 We can observe that the LDA
decomposition of order higher than PDM model is
not necessary for the LDA classifier (for large
feature vector size the maximal LDA size is equal to
(nc-1), where nc is the number of classes). On the
other hand, LDA feature vector size reduction can
ameliorate sensibility of SVM classifier (denoted as
LDA /k & SVM classifier). Influence of class
number on classification sensitivity is presented in
Fig. 9 and 10. Results for nc classes were averaged,
for example for nc=25, testing C100 and learning
LSA sets were divided into 4 separate pairs of
subsets and partial classifications results were
averaged. Results demonstrate that for small number
of classes in relation to the size of feature vector (1),
the SVM classifier is much better then classifier
based on LDA decomposition. This low LDA
classification sensitivity mainly comes from ill-
conditioned between-classes scatter matrix.
Figure 8: Classification sensitivity for LSA and C100 sets.
Figure 9: Classification sensitivity for testing sets Cnc.
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1 6 11 16 21 26 31 36 41 46
Number of eigenvalues p
LSA
C
20%
30%
40%
50%
60%
70%
80%
90%
100%
20 25 30 35 40 45 50 55 60 65
PCA validation size p
LDA /99 {C100}
SVM {C100}
LDA /99 {LSA}
SVM {LSA}
20%
30%
40%
50%
60%
70%
80%
90%
100%
020406080100
D
imension k of LDA subspace
LDA /k {C100}
LDA /k & SVM {C100}
LDA /k {LSA}
LDA /k & SVM {LSA}
SVM lev el {LSA}
SVM lev el {C100}
20%
25%
30%
35%
40%
45%
50%
55%
60%
020406080100
Number of classes nc
LDA /(nc-1)
SVM
(LDA /k & SVM) max
CLASSIFIERS SENSITIVITY FOR BOUNDARY CASE TESTING SET IN THE FACE RECOGNITION ALGORITHM
BASED ON THE ACTIVE SHAPE MODEL
285
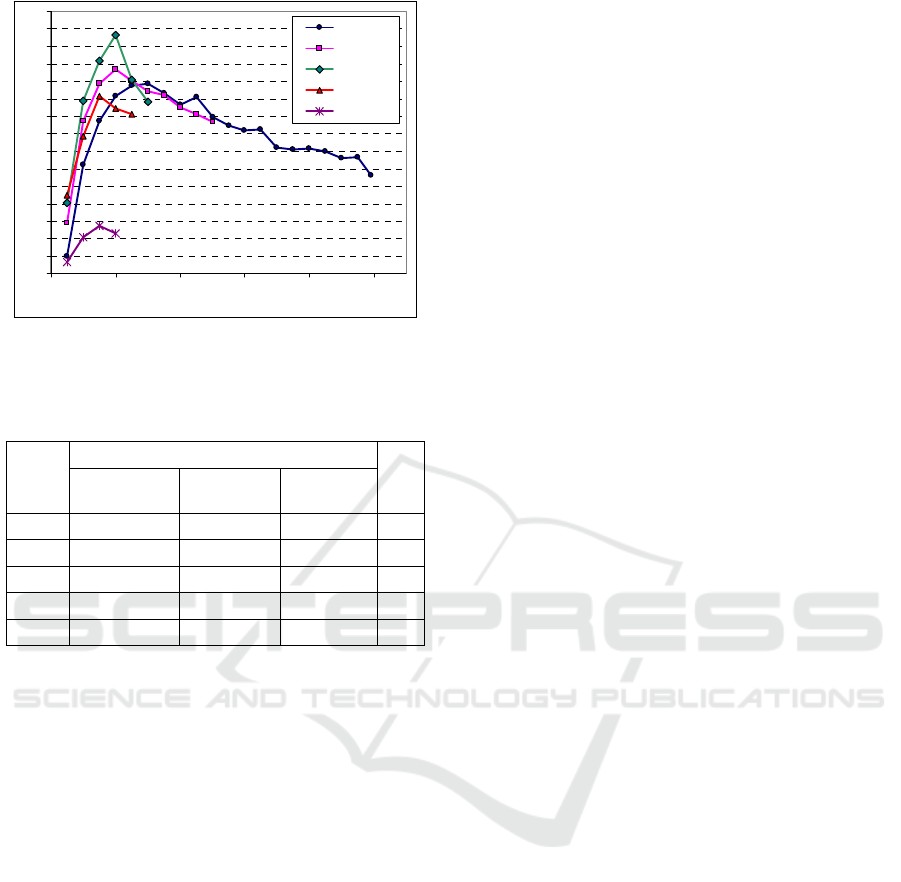
Figure 10: LDA /k & SVM classification sensitivity for
testing sets Cnc.
Table 2: LDA /k & SVM classification sensitivity for
testing sets Cnc.
4 SUMMARY
The ASM produces reasonably good face contours
for our boundary case testing set (Fig. 11 and 12). It
is able to handle face images with glasses, beard and
long hair. We have found out that ASM has
problems with fitting contours to images with non-
frontal face orientation.
It is caused by linear nature of Point Distribution
Model (PDM), which utilizes the PCA validation
procedure (Fig. 4). The PDM validation procedure
filters contours according to the first PCs directions
in the learning set (3 and 4). This is a significant
disadvantage of ASM algorithm which leads to
blurring between-classes differences. Authors in
(Etamad and Chellapa, 1997) underline that the
LDA of faces provides us with a small set of
features that carry the most relevant information for
classification purposes. For medium-sized databases
of human faces, good classification accuracy is
achieved using very low-dimensional feature
vectors.
In this paper, an experiment consisting of
application of boundary case testing set for tuning
ASM parameters and for amelioration of SVM
classifier sensitivity was presented. It has turned out
that same size reduction (according to LDA results)
improves the sensitivity of SVM classifier (Fig. 8
and 10). The optimal size of reduced LDA-subspace
is lower than PDM validation vector size and much
lower than the number of classes k‹‹(nc-1),
investigated in the test (Fig. 10 and Tab. 2). This
condition for size k improves attenuation of
disturbances. Those disturbances are understood as
differences between learning and testing sets
(extreme face positions
under different perspective
variations and facial expressions). Generally, for
large number of classes, the LDA classifier is better
than SVM, but for small number of classes we
observe inverse situation (Fig. 9).
It is desirable to examine influence of other
contour normalisation procedures. In presented
experiments, the height standardisation of face and
nose outlines has not been applied. Other
normalisation procedures, such as application of
initial contour determined by calculated face
position (Ge and Yang, 2005) and identified face
gestures and head position (Wan and Lam, 2005)
will be verified in the future research.
REFERENCES
Cootes, T. and Taylor, C., (2001). Statistical models of
appearance for computer vision, Technical report,
University of Manchester, Wolfson Image Analysis
Unit, Imaging Science and Biomedical Engineering.
Etemad K., Chellappa R. (1997), Discriminant analysis
for recognition of human face images, Springer Berlin
/ Heidelberg.
Ge, X., Yang, J., Zheng, Z., Li, F., (2006). Multi-view
based face chin contour extraction, Engineering
Applications of Artificial Intelligence, vol.19, pp. 545-
555.
Kass, M., Witkin, A., Terzopoulos, D., (1988). Snakes:
Active contour models, International Journal of
Computer Vision, 1 (4), pp. 321-331.
Motulsky, H., (1997). Detecting outliers, GraphPad
Insight, issue number 14, Winter 1997.
Wan, K.W., Lam. K.M., Ng, K.C., (2005). An accurate
active shape model for facial feature extraction,
Pattern Recognition Letters, vol. 26 , Issue 15, pp.
2409-2423.
Zhao, M., Li, S. Z., Chen, Ch., Bu, J., (2004). Shape
evaluation for weighted active shape models,
Proceedings of the Asian Conference on Computer
Vision, pp 1074-1079.
Zuo, F. and de With, P. H N., (2004). Fast facial feature
extraction using a deformable shape model with Haar-
wavelet based local texture attributes, Proceedings of
ICIP’04, vol. 3, pp. 1425-14
20%
22%
24%
26%
28%
30%
32%
34%
36%
38%
40%
42%
44%
46%
48%
50%
0 20406080100
Dimension k of LDA subspace
1 x {C100}
2 x {C50}
3 x {C33}
4 x {C25}
5 x {C20}
No. of
classe
s nc
Classification sensitivity in %
k
max
LDA /(nc-1) SVM
(LDA /k &
SVM)
max
20 29,9 53,2 25,5 15
25 44,9 50,1 40,3 15
33 52,1 46,9 47,3 20
50 49,5 40,9 43,4 20
100 47,6 32,3 41,7 30
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
286

Figure 11: Images and contours from learning set LSA fitted by the ASM algorithm.
Figure 12: Images and boundary case contours from testing set C100 fitted by the ASM algorithm.
CLASSIFIERS SENSITIVITY FOR BOUNDARY CASE TESTING SET IN THE FACE RECOGNITION ALGORITHM
BASED ON THE ACTIVE SHAPE MODEL
287
