
REAL-TIME DENSE DISPARITY ESTIMATION USING CUDA’S API
Mourad Boufarguine, Malek Baklouti, Vincent Guitteny, Serge Couvet
THALES Security Solutions & Services Division (D3S), Cergy-Pontoise, France
Keywords:
Stereovision, Real-time, Range map, Depth map, Dense matching, Beliefs propagation, General purpose cal-
culations on graphic processors.
Abstract:
In this paper, we present a real-time dense disparity map estimation based on beliefs propagation inference
algorithm. While being real-time, our implementation generates high quality disparity maps. Despite the
high complexity of the calculations beliefs propagation involves, our implementation on graphics processor
using CUDA API makes more than 100 times speedup compared to CPU implementation. We tested our
experimental results in the Middlebury benchmark and obtained good results among the real-time algorithms.
We use several programming techniques to reduce the number of iterations to convergence and memory usage
in order to maintain real-time performance.
1 INTRODUCTION
Stereo matching is a fundamental computer vision
problems with a wide range of applications, and hence
it has been extensively studied in the computer vi-
sion field for decades. This paper describes a pro-
grammable graphics hardware implementation of hi-
erarchical beliefs propagation algorithm for stereo vi-
sion within Markov Random Field framework. MRF
formulations of stereo and other early vision prob-
lems have existed for some time, but the computa-
tional and storage complexity make exact solutions
infeasible; exact solutions to MAP estimator are NP-
complete, hence the need for approximation algo-
rithms such as graph cuts and beliefs propagation.
As processing power has increased, the approxima-
tion algorithms have become practical for real-time
stereo applications. Beliefs propagation is well suited
for parallel execution and hardware implementation.
Graphics processing units (GPUs) are highly paral-
lel single -instruction-multiple-data (SIMD) proces-
sors built into modern graphics cards along with up to
512 MB or more of high-speed memory. GPUs and
their programmable interface have become so versa-
tile that much research has been done on performing
general purpose computation in graphics hardware
(GPGPU). GPU computing with CUDA is a new ap-
proach to computing where hundreds of on-chip pro-
cessor cores simultaneously communicate and coop-
erate to solve complex computing problems up to 100
times faster than traditional approaches.
Section 2 describes state-of-the-art stereo match-
ing algorithms. Section 3 describes parallel comput-
ing on GPUs using CUDA API. In section 4, we de-
scribe our implementation of the hierarchical beliefs
propagation. Section 6 draws some conclusions based
on our results exposed in section 5.
2 STEREO MATCHING
ALGORITHMS
Stereo matching is a crucial step in the depth map es-
timation. Despite the simplification brought by the
epipolar geometry, the problem of matching remains
difficult to solve due to occlusion, luminosity changes
between viewpoints and non textured areas. To over-
come these difficulties, several methods have been
proposed. A state of the art of different existing meth-
ods is presented by (Scharstein and Szeliski, 2002).
Stereo matching algorithms are generally classified
into two classes, local algorithms and global algo-
rithms based on the cost computation method.
2.1 Local Methods
Local approaches are based on a correlation criterion
over a local window containing the element to match.
The choice of the appropriate size and shape is crucial
417
Boufarguine M., Baklouti M., Guitteny V. and Couvet S.
REAL-TIME DENSE DISPARITY ESTIMATION USING CUDAâ
˘
A
´
ZS API.
DOI: 10.5220/0001773204170422
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications (VISIGRAPP 2009), page
ISBN: 978-989-8111-69-2
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
to ensure the efficiency of these methods. The choice
of a fixed size is not very wise because it does not
fit all areas of the image. The principle of more ef-
ficient methods is to vary the size (Kanade and Oku-
tomi, 1994) and/or the shape (Veksler, 2002) of the
correlation windows. In (Yoon and Kweon, 2005),
instead of finding the optimal correlation window, the
authors adjust the weight of each pixel in the window.
2.2 Global Methods
Global approaches minimize an overall cost function
that involves all the pixels of the image. It is generally
expressed as an objective energy function
E(d) = E
data
(d) + E
prior
(d) (1)
E
prior
is a regularization term. The formulation
of this term depends heavily on the scene and cho-
sen constraints. Most algorithms use smoothness con-
straint. In this case, the function penalizes the differ-
ence of disparity of neighbouring pixels.
E
data
encodes knowledge about forward image
formation. It assigns a high cost for the functions of
disparity that are not consistent with the data.
In the global methods, calculating the disparity
field is led to minimize the objective function of en-
ergy. Several optimization methods have been pro-
posed such as dynamic programming (Kim et al.,
2005), graph cuts (Roy and Cox, 1998) and beliefs
propagation.
3 BELIEFS PROPAGATION
We model the problem of stereo matching with a
Markov random Field (MRF). We refer the reader
to (Sun et al., 2003). Let P be the set of pixels in
an image and L be a finite set of labels. The labels
correspond to disparities that we want to estimate at
each pixel. A labeling d assigns a label d
p
∈ L to
each pixel p ∈ P. To measure the quality of a labeling
d, we consider the global energy function
E(d) =
∑
p∈P
D
p
(d
p
) +
∑
(p,q)∈N
U
p,q
(d
p
, d
q
) (2)
D
p
and U
p,q
are the data cost and smooth cost respec-
tively. The data cost encodes the log-likelihood func-
tion. The smooth cost encodes the prior distribution.
N is the set of neighboring pixels couples.
3.1 Data and Smooth Costs
To compute the data cost, we use a truncated absolute
difference as the matching cost. We aggregate this
cost over a square window with constant disparity.
D
p
(d
p
) =
∑
(x,y)∈N(p)
min(|I
re f
(x, y) −I
match
(x −d, y)|, T )
(3)
The smooth cost is also computed using a trun-
cated absolute difference.
U
p,q
(d
p
, d
q
) = min(|d
p
−d
q
|, λ) (4)
N(p) is a p-centered square window, I
re f
is the refer-
ence image and I
match
is the target image. T and λ are
thresholds.
3.2 BP Algorithm
In the min-sum form of the BP algorithm, we mini-
mize the global energy function in equation 2.
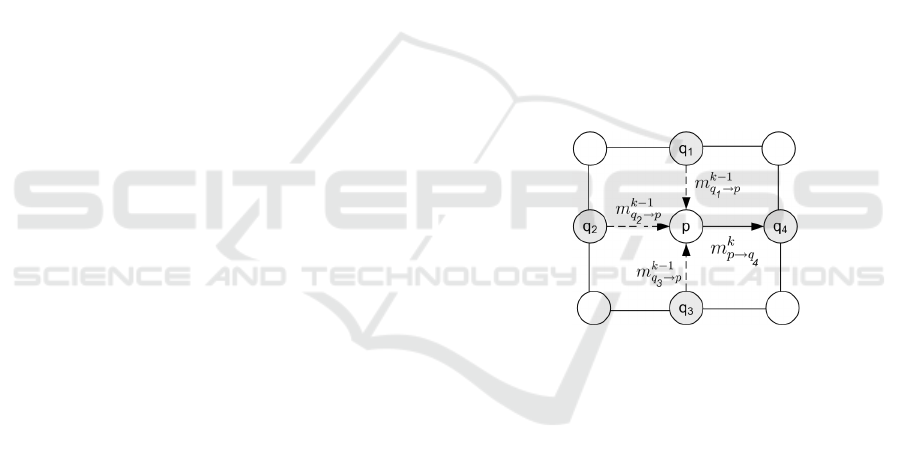
Figure 1: Messages Updates scheme.
BP estimates a MAP labelling for the MRF by
sending messages between nodes (Figure 1). A
node p sends to each of its four neighboors q
i
, i ∈
{1, 2, 3, 4} a message m
k
p→q
i
at every iteration k. Each
message is a vector of length |L|, with each compo-
nent being proportional to how likely node p ”be-
lieves” that node q
i
will have the corresponding dis-
parity. In the min-sum algorithm, messages are up-
dated in the following way
m
k
p→q
i
(d
q
i
) = min
d
p
(D
p
(d
p
) +U
p,q
i
(d
p
, d
q
i
) (5)
+
∑
j∈{1,2,3,4}, j6=i
m
k−1
q
j
→p
(d
p
))
After K iterations, we compute the ”beliefs” vec-
tor for each node p
b
p
(d
p
) = D
p
(d
p
) +
∑
i∈{1,2,3,4}
m
K
q
i
→p
(d
p
) (6)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
418
Finally, for each node p we select the label d
∗
p
that
corresponds to the component of b
p
with the mini-
mum value
d
∗
p
= arg min
d
p
∈L
b
p
(d
p
) (7)
3.3 Complexity Analysis
A standard implementation of the algorithm will be at
best a complexity of O(4 ×W ×H ×|L|
2
×K). Where
W and H are the image dimensions, L the set of dis-
parity values and K the number of iterations. The fac-
tor 4 is due to the fact that four messages are updated
per pixel and per iteration. we notice that the com-
plexity is a quadratic function of the disparity range
(|L|). In fact, to compute each of the |L| values of
the message, we do a minimization through the dis-
parity values of equation 6. Moreover, the number
of iterations to convergence (K) has a complexity of
O(
√
W ×H) in order to propagate information over
all the pixels. Thus, the complexity of computation is
not linear according to the image dimensions.
In addition to its complexity, the beliefs propagation
algorithm has the disadvantage to need a fairly large
memory space. Indeed, we need to save in the mem-
ory, at least for two successive iterations and for each
pixel, the four vectors of |L| components representing
messages.
3.4 Proposed Solution and Algorithm
In this section, we describe how to reduce the com-
plexity of the algorithm. To reduce the complexity of
the algorithm, we propose three solutions :
• reduce the complexity related to the disparity
range from O(|L|
2
) to O(|L|), by exploiting the
properties of the chosen U
p,q
function (eq 4);
• reduce by half the memory space by exploiting the
fact that our graph is bipartite;
• reduce the number of iterations needed for the
convergence of the algorithm, using an hierarchi-
cal approach to update messages.
3.4.1 Reducing the Complexity Related to the
Disparity Range
We can rewrite the equation 6 in the following form:
m
k
p→q
i
(d
q
i
) = min
d
p
∈[d
min
,d
max
]
(U
p,q
i
(d
p
, d
q
i
) + h(d
p
))
(8)
where h(d
p
) = D
p
(d
p
) +
∑
4
j=1, j6=i
m
k−1
q
j
→p
(d
p
).
The usual approach to compute this message, explic-
itly minimizes this term throughout all the possible
values of d
p
. This needs O(|L|
2
) operations (|L| is the
number of disparity values). Using the properties of
the function U
p,q
i
(equation 4), we will demonstrate
how to reduce the complexity to O(|L|).
To simplify the demonstration, let’s consider a non-
truncated function. The update message function is
done then as in equation 9.
m
0
(u) = min
d
p
∈[d
min
,d
max
]
(ρ.min(|d
p
−u|+ h(d
p
)) (9)
for each u ∈ [d
min
, d
max
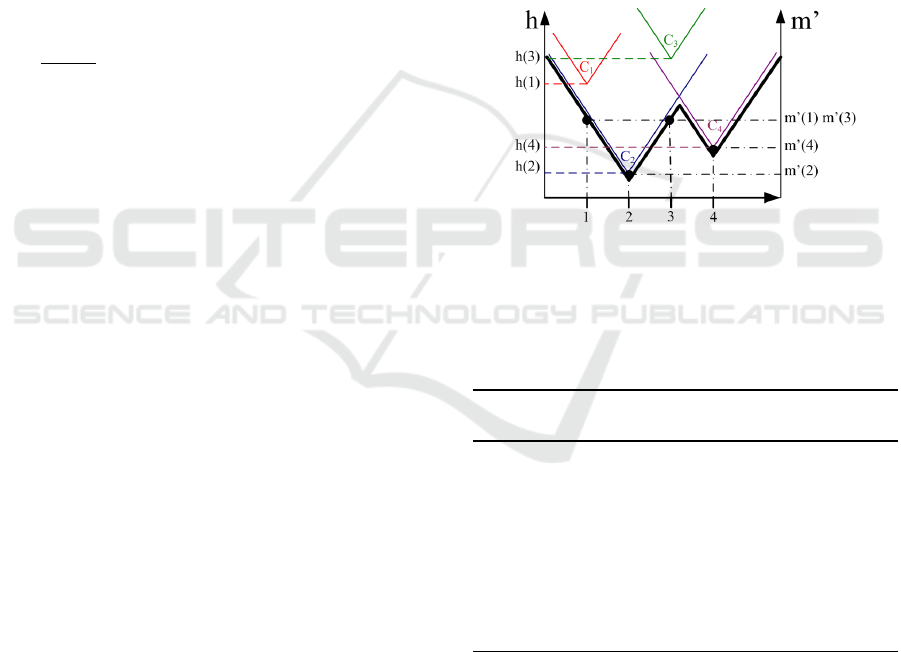
]. The minimisation of equa-
tion 9 can be seen as the convex hull of L cones de-
fined by the parametric equation 10. Figure 2 shows
and example of the convex hull.
C
d
p
: x 7→ ρ
|
d
p
−x
|
+ h(d
p
);d
p
∈ [d
min
, d
max
] (10)
Figure 2: Convex hull of an example of 4 cones.
To compute this hull, we use an algo-
rithm of distance transformation introduced
by (Borgefors, 1986). The algorithm to
compute the messages is detailed below.
Algorithm 1: Algorithm of computation of m’
in O(|L|).
for u = d
min
d
max
do
m
0
(u) ← h(u)
end for
for u = d
min
+ 1 d
max
do
m
0
(u) ← min(m
0
(u), m
0
(u −1) + ρ)
end for
for u = d
max
−1 d
min
do
m
0
(u) ← min(m
0
(u), m
0
(u + 1) + ρ)
end for
Hence, for the truncated function we obtain :
m
k
p→q
i
(d
q
i
) = min
m
0
(d
q
i
), min
d∈[d
min
,d
max
]
h(d) + λ
(11)
3.4.2 Reducing the Memory Usage
The propagation of messages have the property of bi-
partite graph (figure 1). A bipartite graph is a graph
REAL-TIME DENSE DISPARITY ESTIMATION USING CUDA'S API
419

whose vertices can be divided into two disjoint sets
A and B such that every edge connects a vertex in A
to one in B. We notice that in the case of a bipartite
graph, to update the messages sent by the pixels of A,
we only need the messages sent by the pixels of B.
As a result, to compute messages sent by a pixel of A
at iteration k + 1, we need only half of the messages
of the iteration k unlike the classical algorithm. In ad-
dition to the gain in memory space, this technique can
reduce by half the number of operations, since only
half of the messages will be updated at each iteration.
3.4.3 Reduce the Number of Iterations a
Hierarchical Approach
In our implementation, we use a multi-scale grid as
described in (Felzenszwalb and Huttenlocher, 2006)
to reduce the number of iterations to convergence.
The basic idea is to perform BP in different scales
from a coarset scale to a finest one. This technique
allows long range interactions between pixels with a
minimum number of iterations. The messages of a
coarser scale are used to initialise the messages in a
finer scale allowing to dramatically reduce the num-
ber of iterations in that scale.
4 PARALLEL COMPUTING ON
GPUS WITH CUDA API
Graphics processing units (GPUs) have evolved to
performances surpassing 500 GFLOPS. CUDA is a
technology for GPU computing from NVIDIA. It ex-
poses the hardware as a set of SIMD multiprocessors,
each of which consists of a number of multiproces-
sors. These multiprocessors have arbitrary read/write
access to a global memory region called the device
memory, but also share a memory region known as
shared memory. Access times to the device memory
are long, but it is large enough (up to 1.5 GB on some
cards) to store entire data sets. The shared memory,
on the other hand, is small (16 KB) but has much
shorter access times. It acts as an explicitly-managed
cache. Traditional textures can also be stored in the
device memory and accessed in a read-only fashion
through the multiprocessor’s texture cache. In addi-
tion, a limited amount of read-only memory is avail-
able for constants used by all the processors. This is
accessed through the constant cache.
A schematic overview of the hardware model is
shown in Figure 3. In a CUDA program, the de-
veloper sets up a large number of threads that are
grouped into thread blocks. A CUDA thread has a
set of registers and a program counter associated with
Figure 3: CUDA Execution Model.
it. Each thread block is executed on a single multi-
processor. It is possible to synchronize the threads
within a block, allowing the threads to share data
through the shared memory. Communication between
all threads, however, require the use of global mem-
ory. Given that a thread block can consist of more
threads than the number of processors in a multipro-
cessor, the hardware is responsible for scheduling the
threads. This allows it to hide the latency of fetches
from device memory by letting some threads perform
computations while others wait for data to arrive.
5 CUDA IMPLEMENTATION
STRATEGY
The implementation strategy has a great impact on
the overall performance of the implementation. It
deals with the allocation of threads to the problem and
the usage of the different types of onboard memory.
The approach chosen uses a thread to process a sin-
gle pixel. The reference image is then divided into
blocks having the same dimensions. Threads within
a same threads block can communicate through the
low latent shared memory. The next step is to deter-
mine what types of memory to use. Texturing from
a CUDA Array is used for both the reference and
target images. Using texturing provides several ad-
vantages mainly a cached access. Global memory is
used to save the data costs and the messages. While
using global memory is bandwidth limiting because
of its latency (400 to 600 clock cycles), the use of
shared memory is inadequate since the treatement of
one block of pixels is dependent on its neighbouring
blocks. Figure 4 shows the instruction flow (single
arrows) and the data flow (double arrows) of our im-
plementation.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
420

Reference
image
Target
image
texture memory
texture memory
Data cost
computing
Message updating
Messages
Global memory
Number of
iterations
Number of
sacles
Disparity
computation
Data costs
Global memory
Figure 4: CUDA implementation details.
6 EXPERIMENTAL RESULTS
We tested our real-time BP algorithm on a 3 GHz
PC equipped with a Geforce 8800 GTS graphics card
with 512M video memory. In the proposed algorithm,
we have two parameters T and λ used in the data and
smooth costs computation modules (equations 3 and
4).
All kernels are implemented using CUDA API.
The same parameter settings were used throughout
the experiments with the following parameters T =
20, λ = 3.0. We implement hierarchical BP in GPU
with three scales, and the typical iterations for each
scale are (4,5,5), from coarse-to-fine scale.
Figure 5 shows the results we obtained for sequences
of the benchmark Middlebury. The table 1 reproduces
the classification by the benchmark Middlebury of our
results compared to some algorithms listed. It is note-
worthy that our algorithm is the 23
rd
place in the over-
all standings, and 2
nd
in the ranking algorithms real
time.
(a) Tsukuba (b) Venus (c) Teddy (d) Cones
Figure 5: Disparity map estimation on sequences from Mid-
dlebury database.
Table 1: Classification by the benchmark Middlebury.
Algorithm Rank % false matching
TsukubaVenusTeddyCones
AdaptingBP (Klaus et al., 2006) 2.8 1.11 0.10 4.22 2.48
RealtimeBP (Yang et al., 2006) 21.9 1.49 0.77 8.72 4.61
Our implementation 23.2 1.59 1.13 12.6 6.27
RealTimeGPU (Wang et al., 2006) 26.8 2.05 1.92 7.23 6.41
BP+MLH (Scharstein and Szeliski, 2002) 32.5 4.17 1.96 10.2 4.93
The implementation of the non-hierarchical
algorithm takes approximately 14 ms per iteration
(70 iterations per second). The choice of the number
of iterations is empirical and depends on the desired
quality of the disparity map.
The hierarchical approach of the algorithm reduces
the number of iterations required. In our implemen-
tation, we used three scales. At each level, the image
is downscaled by two from a scale to another. In our
implementation, we chose to take one pixel on two to
move from a scale to another.
Table 2: Comparaison between CPU and GPU computing
times (Tsukuba sequence).
Computing Time (ms) FPS (fps)
CPU 4542 0.22
GPU 37 27
We obtained a frame rate of 27 FPS. To estimate
the acceleration of the algorithm done with the GPU,
we implemented the same algorithm on CPU and we
used the same settings (table 2). The CPU takes 4.54
seconds to calculate a disparity map, which corre-
sponds to 0.22fps. We have thus obtained an accel-
eration of 122 times compared to CPU.
(a) Refernece image (b) Disparity map
Figure 6: Disparity map estimation on videos from Mi-
crosoft Research.
Figure 6 shows the estimated disparity map of a
stereo sequence of 320x240 from Microsoft Research.
Our implementation computes 25 frames per second
to estimate a 40 levels disparity map.
Figure 7 shows the estimated disparity map of a
stereo images of 320x240 taken by two DALSA cam-
eras. Our implementation computes 26 frames per
second to estimate a 35 levels disparity map.
REAL-TIME DENSE DISPARITY ESTIMATION USING CUDA'S API
421

(a) Reference image (b) Disparity map
Figure 7: Disparity map estimation on our own sequence.
7 CONCLUSIONS
Algorithms achieving high frame rates must have
strong limitations in image size and disparity search
range, whereas high quality results often need sev-
eral minutes per image pair. We have presented in
this paper a real time dense disparity estimation us-
ing CUDA API. GPU computing with CUDA is a
new approach for parallel computing that supports the
parallel data cache and thread execution manager for
higher efficiency. We have presented in this paper
a new parallel implementation of the efficient belief
propagation algorithm. This allows real time compu-
tation and robustness is clearly demonstrated on the
dedicated Middleburry benchmark.
We reduced the complexity of the algorithm using a
distance transformation to minimize the convex hull
for message computation. We reduced then the mem-
ory usage using bipartite graph properties. Finally, we
used a multi-scale grid to reduce the number of itera-
tions to convergence. In our implementation, we per-
formed parallelized message updates thanks to CUDA
progamming.
We tested our real-time BP algorithm on a 3 GHz
PC equipped with a Geforce 8800 GTS graphics card
with 512M video memory. We implemented hierar-
chical BP in GPU with three scales, and the typical it-
erations for each scale are (4,5,5), from coarse-to-fine
scale. We used the Tsukuba data set with 16 disparity
levels and we obtained 27 fps.
REFERENCES
Borgefors, G. (1986). Distance transformations in digi-
tal images. Comput. Vision Graph. Image Process.,
34(3):344–371.
Felzenszwalb, P. F. and Huttenlocher, D. P. (2006). Efficient
belief propagation for early vision. Int. J. Comput.
Vision, 70(1):41–54.
Kanade, T. and Okutomi, M. (1994). A stereo matching
algorithm with an adaptive window. IEEE Trans. Pat-
tern Anal. Mach. Intell., 16(9):920–932.
Kim, J. C., Lee, K. M., Choi, B. T., and Lee, S. U. (2005).
A dense stereo matching using two-pass dynamic pro-
gramming with generalized ground control points. In
CVPR05, pages 1075–1082.
Klaus, A., Sormann, M., and Karner, K. (2006). Segment-
based stereo matching using belief propagation and a
self-adapting dissimilarity measure. In ICPR06, pages
15–18.
Roy, S. and Cox, I. J. (1998). A maximum-flow formulation
of the n-camera stereo correspondence problem. In
ICCV98, page 492.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. Int. J. Comput. Vision, 47(1-3):7–42.
Sun, J., Shum, H., and Zheng, N. (2003). Stereo matching
using belief propagation. IEEE Trans. Pattern Anal.
Mach. Intell., 25(7):787–800.
Veksler, O. (2002). Stereo correspondence with compact
windows via minimum ratio cycle. IEEE Trans. Pat-
tern Anal. Mach. Intell., 24(12):1654–1660.
Wang, L., Liao, M., Gong, M., Yang, R., and Nister, D.
(2006). High-quality real-time stereo using adap-
tive cost aggregation and dynamic programming. In
3DPVT06, pages 798–805.
Yang, Q., Wang, L., and Yang, R. (2006). Real-time global
stereo matching using hierarchical belief propagation.
In BMVC06, page III:989.
Yoon, K.-J. and Kweon, I.-S. (2005). Locally adaptive
support-weight approach for visual correspondence
search. In CVPR05, pages 924–931.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
422
