FACIAL NORMAL MAP CAPTURE USING FOUR LIGHTS

An Effective and Inexpensive Method of Capturing the Fine Scale

Detail of Human Faces using Four Point Lights

Jasenko Zivanov, Pascal Paysan and Thomas Vetter

Computer Science Department, University of Basel, Bernoullistrasse 16, 4056 Basel, Switzerland

Keywords:

Face rendering, Face normal map, Normal map capture, Surface reconstruction.

Abstract:

Obtaining photorealistic scans of human faces is both challenging and expensive. Capturing the high-

frequency components of skin surface structure requires the face to be scanned at very high resolutions, outside

the range of most structured light 3D scanners.

We present a novel and simple enhancement to the acquisition process, requiring only four photographic ﬂash-

lights and three texture cameras attached to the structured light scanner setup.

The three texture cameras capture one texture map (luminance map) of the face as illuminated by each of the

four ﬂash-lights. Based on those four luminance textures, three normal maps of the head are approximated,

one for each color channel. Those normal maps are then used to reconstruct a 3D model of the head at a much

higher mesh resolution, in order to validate the normals. Finally, the validated normals are used as a normal

map at rendering time. Alternatively, the reconstructed high resolution model can also be used for rendering.

1 INTRODUCTION

Humans are exceedingly adept at detecting errors in

computer-generated faces, as we have a lifetime of ex-

perience observing real ones. At the same time, faces

are among the objects one would most often want to

render, as they provide a unique way to reach out to

an audience and communicate ideas and impressions.

Two things make the realistic rendering of faces

difﬁcult. One is ﬁne scale skin detail, visible almost

exclusively by the inﬂuence it has on shading patterns,

the other is its translucency, and especially the fact

that skin is far more translucent under red light than

under green or blue light (Jensen et al., 2001).

While there are means of capturing high resolu-

tion detail in entire faces, they are limited to excep-

tionally precise range scanners and light domes con-

taining thousands of light sources, both of which are

rather expensive. Our approach sacriﬁces some preci-

sion in order to perform the same task by using only

four point light sources. Care is taken, however, not

to impair the visual quality of the result - images ren-

dered using the resulting model or normal maps re-

main visually credible, even if they do not allow for

an exact reconstruction of a photograph of the same

head.

By estimating a separate normal map for each

color channel, we can also capture some effects of

subsurface scattering. Since red light tends to travel

further inside skin before leaving it than green or blue

light, skin appears smoother when observed under red

light. As a consequence, darker points on the skin sur-

face appear more red than lighter points.

2 RELATED WORK

Barsky and Petrou (Barsky and Petrou, 2001) present

a normal estimation technique somewhat similar to

ours. They offer a method to estimate the normals

of a non-translucent lambertian surface by evaluating

photographs taken under different simple illumination

conditions. Deviations of the surface from a lamber-

tian reﬂectiveness, caused by both an inhomogenous

distribution of incoming light and the non-lambertian

reﬂectance of the material itself, introduce an error

in the lower frequency bands of the resulting normal

map. An example of this can be seen in Fig. 1.(b).

Nehab et al (Nehab et al., 2005) present a

method to combine the low frequency bands of a

range scanned model with higher frequencies ob-

tained through photometric stereo. The method is

aimed at the capture of smaller objects, though, and

does not appear suitable for human faces. Weyrich

Zivanov J., Paysan P. and Vetter T. (2009).

FACIAL NORMAL MAP CAPTURE USING FOUR LIGHTS - An Effective and Inexpensive Method of Capturing the Fine Scale Detail of Human Faces

using Four Point Lights.

In Proceedings of the Four th International Conference on Computer Graphics Theory and Applications, pages 13-20

DOI: 10.5220/0001773300130020

 SciTePress

et al (Weyrich et al., 2006) apply the two methods

to capture high resolution meshes of faces. In con-

trast to us, however, they use well above 1000 light

sources, each of which has been painstakingly cali-

brated by taking photographs of a disk of Fluorilon, a

material with an almost ideally lambertian reﬂective-

ness, at different positions inside the individual light

cones.

Haro et al (Haro et al., 2001) use silicone molds

of skin to acquire normal maps of patches of the fa-

cial surface, and then grow the resulting pattern to

cover the entire face using a texture synthesis tech-

nique. The approach is unable to capture local ﬁne

scale features speciﬁc to a person such as wrinkles,

moles and scars. It also ignores the translucency of

skin, although its effects could be computed at ren-

der time, for example through the use of texture space

convolution as in (Borshukov and Lewis, 2003). Us-

ing the geometrically correct normal maps without

addressing the effects of translucency, however, leads

to grainy-looking and sandpaper like skin.

Debevec et al (Ma et al., 2007) offer a scan-

ning technique that produces four independent nor-

mal maps, one for the diffuse reﬂection in each of the

three color channels and one for specular reﬂections.

The lighting setup they use is fairly complex though,

as the technique relies on polarized full sphere illumi-

nation.

3 SETUP

We use a structured light 3D scanner system for the

geometry acquisition. The texture is captured using

three high resolution SLR cameras and four photo-

graphic ﬂash lights. The ﬂash lights have an effect on

the face similar to that of theoretical point lights.

The positions of the ﬂash lights have been deter-

mined by scanning a number of taut strings running

together at each of the lights and intersecting the mea-

sured lines in space. When choosing where to place

the lights, care has been taken to maximize areas of

the face lit by at least three lights.

The light intensity distributions of the light cones

do not need to be known, as long as the light intensity

varies only smoothly along the surface. If this is the

case, the light intensity can only have an impact on the

low frequency component of the estimated normals,

while only the high frequencies are taken from the

photographs - the low frequencies can be extracted

from shape.

4 PROCEDURE

After scanning the face using the structured light cap-

ture process, which takes about half a second, the four

ﬂash lights are triggered in quick succession, and four

images are captured by each of the three cameras. The

overall scanning process takes approximately three

seconds.

The twelve photographs are then mapped into the

head’s texture space, resulting in twelve texture maps.

Ray tracing is applied to calculate the self-occlusion

of the face in regard to the cameras and the light

sources.

Before the normal estimation process is initiated,

the four sets of three images are used to reduce the

effects of specularity. This is done by forming min-

ima over the triples of textures captured by the three

cameras under each of the four lights.

We are then left with only four textures of the face,

one for each light source. As most areas of the face

contain shadows in at least one of the textures, we es-

timate most of the normals based on three color val-

ues.

Those normals carry a systematic bias due to the

varying intensity of incoming light across the face,

as our light sources are in reality photographic ﬂash-

lights that spread light inside a cone, and not perfect

point lights. That bias is removed by ensuring that the

average normal direction in a certain area is perpen-

dicular to the surface of the 3D model in that area.

Finally, photographic noise is removed from the

normal maps by reconstructing the 3D-surface at the

resolution of the normal maps, and using the normals

implied by that surface. The surface itself can also be

used as a high-resolution model of the face.

5 SPECULARITY REDUCTION

Specularity is considered a necessary evil in our ap-

proach. Although it carries the most precise nor-

mal information (as specularly reﬂected light does not

succumb to subsurface scattering), the coverage of the

face by intense specularity in our setup is simply in-

sufﬁcient to allow for a stable estimation of specular

normals and the spatially varying specular reﬂectance

function.

Let P

icl

be pixel i of the radiance texture of

the head taken by camera c under light l. Essen-

tially, what we are interested in, is the value P

min

icl

). As diffusely reﬂected light is assumed to

spread out evenly in all directions, while specularly

reﬂected light is focused in one particular direction,

looking at a point on the surface from the direction

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

(a) (b)

Figure 1: Outline of the capture process. The initial normals

(a) are calculated from the geometry of the mesh. The po-

sitions of multiple vertices are taken into account when the

normal of each vertex is computed, thus the smooth appear-

ance. Photographs of the face are used to estimate the raw

normal maps (b). Low frequencies from (a) and high fre-

quencies from (b) are combined to compute the corrected

normal map (c), which is then used to reconstruct a high

resolution surface, yielding the ﬁnal reconstructed normal

map (d).

from which it is seen the darkest, also yields the color

closest to the diffuse color of the surface at that point.

Forming the minimum in this naive way would

however create discontinuities in image color at vis-

ibility borders and introduce edges into the resulting

normal map. In order to avoid this, the borders are

interpolated smoothly, using an offset negative gaus-

sian of the distance of each texel to the border as its

weight.

The suppression of specularity could also be per-

formed using cross polarization, ie. placing polariz-

ing ﬁlters in front of the camera and the light source,

though great attention would have to be paid to the

orientation of the ﬁlters, as the cameras and the light

sources are not located in a plane in space.

Now that specular reﬂections have been removed

from the input textures, those textures can be used to

estimate normal maps.

5.1 Normal Estimation

After our specularity reduction step, we are left with

four images of the the diffuse radiance of the head, as

seen under the four light sources.

Assuming lambertian reﬂection, we can express

the luminance of color channel λ ∈ {R,G,B} of texel i

under light l as a dot product of

→

iλ

, the normal we are

looking for, and

→

, the normalized vector pointing

towards the light, scaled by the surface albedo a

iλ

ilλ

= a

iλ

→

iλ

If the texel is in shadow under only one light,

which is mostly the case, we can simply solve the fol-

lowing linear system of equations, once for each color

channel:

iλ







→







→

iλ





i0λ

i1λ

i2λ





Note that we are only interested in the direction of

→

iλ

at this point, so the value of a

iλ

that only scales

the normal can be ignored.

What remains is a linear system of equations with

three unknowns and three equations. If the texel is

visible under all four lights, we even have an overde-

termined linear system of the same form, that we can

solve in the least squares sense. Due to our setup,

the overdetermined texels usually form a thin vertical

band in the middle of the face.

Either way, solving the system yields the scaled

normal a

iλ

→

iλ

. We could hypothetically keep the

length of a

iλ

→

iλ

as the value of a

iλ

, but doing so

would introduce irregularities in facial color, as the

normal

→

iλ

still suffers from a low frequency error.

Instead, we only normalize the resulting normal.

5.2 Low Pass Correction

The resulting normal maps still suffer from a system-

atic low frequency error caused by the inhomogenous

distribution of incoming light and deviations from

lambertian reﬂection (see Fig 1.(b) for an example).

That error can be reduced by discarding the low fre-

quency part of the normal map and replacing it with

the low frequency data from the 3D model. We call

that process the low pass correction.

The low pass correction is performed separately

for the ﬁve facial areas - the four areas illuminated by

all but one of the four lights, and the area illuminated

FACIAL NORMAL MAP CAPTURE USING FOUR LIGHTS - An Effective and Inexpensive Method of Capturing the

Fine Scale Detail of Human Faces using Four Point Lights

by all four lights. The reason for this is that the ﬁve

areas exhibit different low frequency errors, as the er-

ror caused by each light nudges the estimated normal

in a different direction.

Let N

sharp

be the normal map we have just ob-

tained, N

blur

a low-pass ﬁltered version of that nor-

mal map and N

vertex

a low-pass ﬁltered normal map

generated from the 3D geometry, which is created by

rendering the vertex normals into texture space.

We deﬁne a new normal map N

comb

as follows:

comb

:= N

sharp

+ N

vertex

− N

blur

comb

has the useful property that when it is itself low-

pass ﬁltered, the result is very close to N

vertex

- the

low frequencies of N

comb

consist of information from

vertex

, while only the high frequency information is

taken from N

sharp

. This is highly useful, as variations

in incoming light intensity are always of a low fre-

quency nature.

Since the correction is performed on each vector

component independently, the resulting normals have

to be renormalized.

Our method is similar to the one presented in (Ne-

hab et al., 2005), except that we perform the low-pass

ﬁltering by convolving the normal map linearly with

a gaussian kernel, instead of estimating a rotation ma-

trix for each normal - we assume that the difference

in the lower frequency bands is small enough for that

not to make any difference.

Once the ﬁve patches of N

comb

have been com-

puted for all ﬁve areas, they can be safely put to-

gether - because they all share the same low frequency

information, there is no longer any danger of edges

(discontinuities in the normal map) appearing at the

seams.

At points illuminated by only two or less lights

(the sixth area), the original vertex normal map,

vertex

, is used.

After the low pass correction, the normal map

looks like Fig. 1 (c). In order to render images with it,

a texture containing the surface albedo is needed. The

albedo a

for color channel λ is deﬁned as the ratio

of light of color λ that is reﬂected off a surface, when

the incoming light direction is perpendicular to it.

5.3 Albedo Estimation

Only after the low pass correction has been com-

pleted, is it safe estimate the surface albedo.

We deﬁne the albedo a

iλ

for texel i and color chan-

nel λ as follows:

iλ

∑

valid l

(

→

iλ

ilλ

∑

valid l

(

→

iλ

)

→

iλ

is the estimated surface normal at texel i for

color channel λ,

→

is the normalized vector towards

light l and I

ilλ

is the λ channel of the diffuse lumi-

nance of texel i under light l. The expression can be

seen as a weighted average over the individual contri-

butions I

ilλ

→

iλ

), weighted by the squared lam-

bert factors (

→

iλ

)

. The weights are squared in

order to suppress the inﬂuence of dark pixels, where

the relative error is the largest.

At the end, the albedo is grown into areas where

it is undeﬁned. This is done so tiny cracks can be re-

moved that can form mostly around the lips, where

occlusion is critical and the texture resolution is low

(in our case). This is done by setting the value of each

undeﬁned pixel to the average value of all deﬁned

neighboring pixels (after which the pixel becomes de-

ﬁned), and repeating the procedure a number of times.

Although the data computed so far is sufﬁcient to

render images, the quality of the normal maps can still

be improved. This is done by computing a 3D surface

at the resolution of the normal map with surface nor-

mals that match those of the normal map as closely as

possible. The normals of that surface are then used as

a more realistic normal map.

5.4 Surface Reconstruction

Not every vector ﬁeld is a possible normal map - at

least not as long as the surface it is supposed to repre-

sent has been adequately ﬁltered prior to sampling.

We are looking for a normal map that actually cor-

responds to a real surface. By enforcing that fact,

we can remove part of the photographic noise that

has found its way into the normals without sacriﬁcing

higher frequency bands of the normal map. We do

that by reconstructing the surface at the resolution of

the normal map. The reconstructed surface can then

be either rendered directly or its surface normals can

be written into a normal map, and the original, coarse

mesh rendered using that normal map.

If the normal map is to be used with the coarse

mesh, the normal maps for all three color channels

have to be used to reconstruct three different meshes.

If the high resolution mesh is to be used for render-

ing, only one of the meshes has to be reconstructed,

preferrably the one corresponding to the green chan-

nel. The effects of subsurface scattering on the color

of skin are thereby lost. The green channel is chosen

because it offers the best trade-off between signal in-

tensity and contrast, because the normals correspond-

ing to the red channel are much softer, while the ones

corresponding to the blue channel are noisy as only

very little blue light is reﬂected off human skin.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

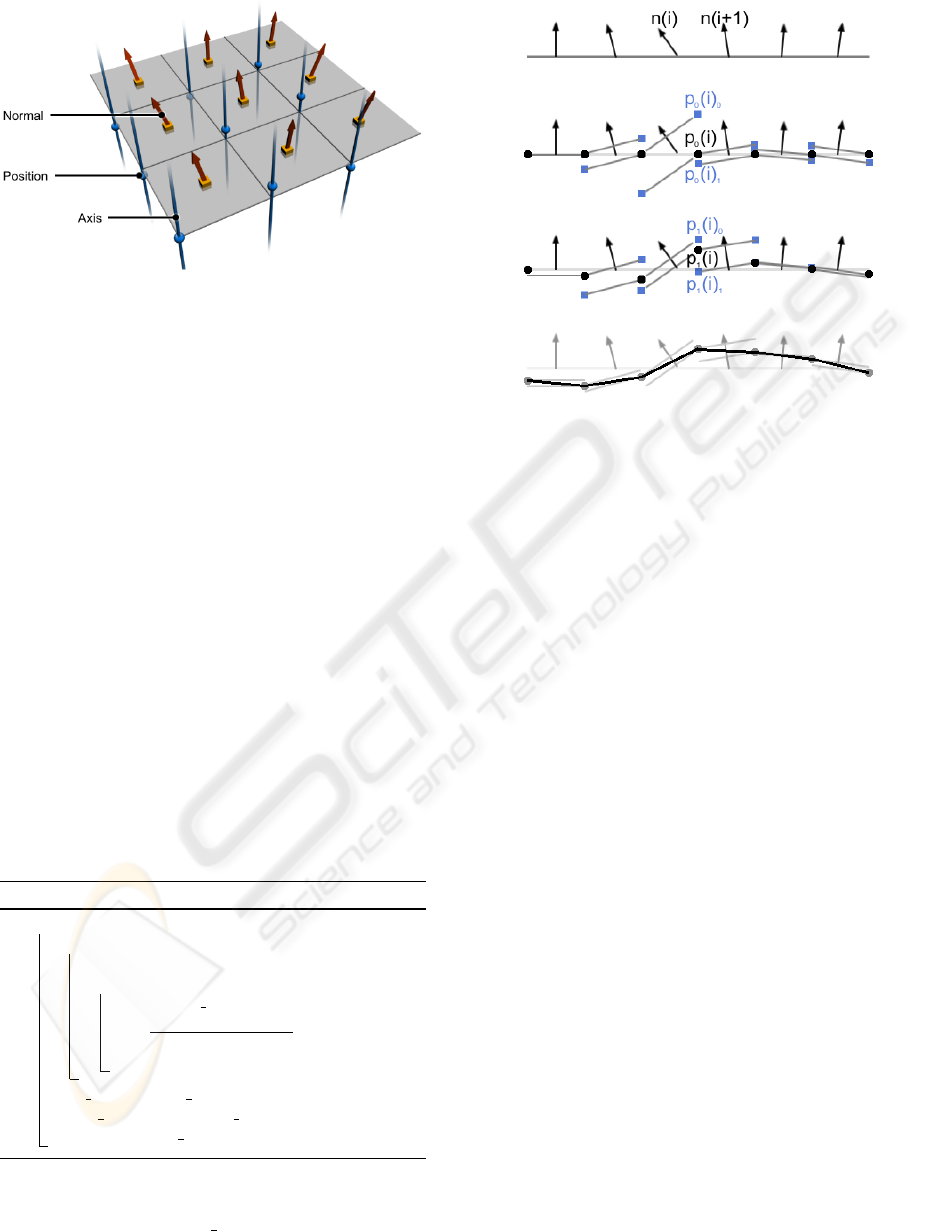
Figure 2: The setup for our surface reﬁnement process.

Note that the positions are placed between the normals of

the normal map.

The surface reconstruction is again similar to (Ne-

hab et al., 2005), although we use an iterative non-

linear method instead of attempting to deal with a

×10

(albeit sparse) matrix. The size of the prob-

lem stems from the fact that the displacement of each

texel is given by the normal map only as relative to its

neighboring texels.

Our procedure looks as follows:

Let N

comb

be the original normal map, and P

texture holding the 3D positions of each texel. P

deﬁned in such a way that an entry P

(x,y) holds the

3D position of the surface between the four normal

map entries N

comb

(x,y), N

comb

(x + 1,y), N

comb

(x,y +

1) and N

comb

(x + 1,y + 1), as illustrated in Fig. 2.

Furthermore, for each texel P

(x,y), a correspond-

ing axis A(x,y) is deﬁned, parallel to the interpolated

vertex normal at that point. It is along that axis, that

the position P

(x,y) is allowed to move.

The position P

i+1

(x,y) for each successive itera-

tion is obtained using the following algorithm:

Algorithm 1: Geometry Reﬁnement.

for i ∈ {0 ... iterations} do

for (x

) ∈ texels do

error[x

] = 0;1

for (x

) ∈ neighborhood(x

) do

n = normal between((x

),(x

));2

ε =

dot(P

]−P

],n)

dot(A[x

],n)

;

error[x

] += weight(x

) · ε;4

avg error = gauss convolution(error);5

norm error = error - avg error;6

i+1

= P

- norm error ·A;7

The process is illustrated in 2D in ﬁgure 3.

The function normal between((x

),(x

))

returns the normal from the normal map N

comb

be-

Figure 3: An illustration of our surface reconstruction al-

gorithm as applied to a 2D normal map. The black circular

dots represent the current positions, while the blue square

dots are where the neighboring texels at their current po-

sitions require the positions to be. Please note that all 2D

normal maps in fact correspond to valid 2D-surfaces (ie.

piecewise linear functions), which is not the case with all

3D normal maps.

tween (x

) and (x

) if they are diagonal neigh-

bors, and the normalized average of the two normals

in between, if they are not (see Fig. 2).

The variable denoted ε in the code tells by how

much point P

] has to be shifted along A[x

]

in order for the straight line between P

] and its

neighbor P

] to be perpendicular to n. The sum

of the weight terms of all neighbors has to be one or

less. The weight of diagonal neighbors has been cho-

sen as half as much as the weight of direct neighbors

in our case.

The error is normalized prior to the computation

of P

i+1

, as we are only interested in its high frequency

component - on a coarser scale, the mesh is assumed

to be correct.

Depending on texture resolution, between 20 and

50 such iterations are required to approach a state of

equilibrium.

6 RESULTS

Our method allows for the reconstruction of high res-

olution surface detail of human faces using only very

limited information as input. For this reason, the

method is also susceptible to missing data, in the

form of shadows cast by the face onto itself. This

is problematic, because both the positions of the light

FACIAL NORMAL MAP CAPTURE USING FOUR LIGHTS - An Effective and Inexpensive Method of Capturing the

Fine Scale Detail of Human Faces using Four Point Lights

(a) (b)

(e) (f)

Figure 4: The surface reconstruction process using a 512 ×

512 normal map and a 128 ×128 mesh, resulting in a 512×

512 mesh. The initial surface (a, b), the surface after one

iteration (c, d) and after 41 iterations (e, f).

sources and the shape of the face casting the shadows

are only known up to a certain degree of accuracy.

The four ﬂash lights were mounted approximately

35 degrees left and right and 15 degrees up and down

in front of the person to scan. That arrangement has

been chosen to minimize areas shadowed under more

than one light. Although points illuminated by only

two or less of the four lights can be ﬁlled in using

the original vertex normals as a fallback, care has to

be taken to calculate the shadows using an adequate

margin of error. If shadowed texels are not ﬁltered

out strictly enough, they will inﬂuence the resulting

normals. At the same time, we can not afford to lose

too many lit texels in the proximity of shadowed re-

gions. The artifacts arising from inadequately sup-

pressed shadows are illustrated in Fig 6.

The estimated normals for all three color channels

are shown in Fig 7. Note that the normals based on

the red channel are much smoother than those based

on the blue channel. This can be explained by the

more extensive scattering of red light in the deeper

layers of the skin (see (Jensen et al., 2001)).

Comparisons between renderings created using

geometric normals and our estimated normal maps

can be seen in Fig. 5 and 8. The geometric nor-

mals have been computed at each vertex by averaging

the normals of nearby triangles. The algorithm takes

about eleven minutes on an Intel Core2 6600 2.40GHz

for one 1024 × 512 normal map. Overall, the method

provides visually convincing results, while the cost

of the required additional hardware remains relatively

low (below 1000 USD, given an existing structured

light scanner).

ACKNOWLEDGEMENTS

This work was partially funded by the NCCR CO-ME

project number 5005-66380.

REFERENCES

Barsky, S. and Petrou, M. (2001). Colour photometric

stereo: simultaneous reconstruction of local gradient

and colour of rough textured surfaces. Eighth IEEE

International Conference on Computer Vision, 2:600–

605.

Borshukov, G. and Lewis, J. (2003). Realistic human face

rendering for” The Matrix Reloaded”. International

Conference on Computer Graphics and Interactive

Techniques, pages 1–1.

Haro, A., Guenter, B., and Essa, I. (2001). Real-time,

Photo-realistic, Physically Based Rendering of Fine

Scale Human Skin Structure. Rendering Techniques

2001: Proceedings of the Eurographics Workshop in

London, United Kingdom, June 25-27, 2001.

Jensen, H., Marschner, S., Levoy, M., and Hanrahan, P.

(2001). A practical model for subsurface light trans-

port. Proceedings of the 28th annual conference on

Computer graphics and interactive techniques, pages

511–518.

Ma, W., Hawkins, T., Peers, P., Chabert, C., Weiss, M., and

Debevec, P. (2007). Rapid acquisition of specular and

diffuse normal maps from polarized spherical gradient

illumination. Submitted to EGSR.

Nehab, D., Rusinkiewicz, S., Davis, J., and Ramamoorthi,

R. (2005). Efﬁciently combining positions and nor-

mals for precise 3D geometry. Proceedings of ACM

SIGGRAPH 2005, 24(3):536–543.

Weyrich, T., Matusik, W., Pﬁster, H., Bickel, B., Donner,

C., Tu, C., McAndless, J., Lee, J., Ngan, A., Jensen,

H., et al. (2006). Analysis of human faces using a

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

measurement-based skin reﬂectance model. Interna-

tional Conference on Computer Graphics and Inter-

active Techniques, pages 1013–1024.

APPENDIX

(a)

(b)

Figure 5: Renderings of a face under omnidirectional light-

ing from the Ufﬁzi light probe. The original geometric nor-

mals can be seen in (a) and the highly detailed normals ob-

tained through our method in (b).

(a) (b)

Figure 6: Possible failure scenarios: points inside shadows

are not discarded strictly enough (a), so the shadow of the

nose leaves an imprint on the normal map, or they are dis-

carded too strictly (b), creating a gap in the normal map at

the center of the nose.

(a) (b) (c)

Figure 7: Shaded normal maps for the red (a), green (b) and

blue (c) channel. Note that the perceived smoothness of the

surface increases with greater wavelength.

(a) (b)

Figure 8: More renderings under a point light using geo-

metric normals (a, c) and our normal map (b, d).

FACIAL NORMAL MAP CAPTURE USING FOUR LIGHTS - An Effective and Inexpensive Method of Capturing the

Fine Scale Detail of Human Faces using Four Point Lights

(a)

(b)

(c)

Figure 9: Renderings of normal mapped heads under a point

light.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications