
COLOR-PRESERVING DEFOG METHOD
FOR FOGGY OR HAZY SCENES
Dongbin Xu, Chuangbai Xiao
Beijing University of Technology, Beijing, China
Jing Yu
Department of Electronic Engineering, Tsinghua University, China
Keywords: Defog, Retinex, Image Enhancement.
Abstract: Bad weather, such as fog and haze, can significantly degrade the imaging quality, which becomes a major
problem for many applications of computer vision. In this paper, we propose a novel color-preserving defog
method based on the Retinex theory, using a single image as an input without user interactions. In the
proposed method, we apply the Retinex theory to fog/haze removal form foggy/hazy images, and conceive a
new strategy of fog/haze estimation. Experiment results demonstrate that the proposed method can not only
remove fog or haze present in foggy or hazy images, but also restore real color of clear-day counterparts,
without color distortion. Besides, the proposed method has very fast implementation.
1 INTRODUCTION
Many outdoor applications of vision community
such as surveillance, target tracking and object
recognition, require high quality input images to
detect robust features. Unfortunately, the visibility
and color of images are degraded greatly under bad
weather condition, especially foggy/hazy weather.
Therefore, it is imperative to enhance visual quality
and good visibility of the degraded images.
The exact nature of fog/haze is very complex and
depends on many factors including the types,
orientations, size and distributions of particles,
polarization states and directions of the incident light
(Narasimhan & Nayar, 2003a). In the literature,
many approaches have been proposed to tackle the
problem. General contrast enhancement is obtained
by tone-mapping techniques including linear
mapping, histogram stretching and equalization, and
gamma correction. However, these methods perform
poorly for the problem mentioned above.
Incorporating local information, some more
sophisticated operators (Stark, 2001; Kim et al.,
2002) achieve relative good performance at the cost
of computational complexity. Recently, some
approaches provide impressive results by assuming
the scene depth (Narasimhan & Nayar, 2003b), two
photographs given (Shwartz et al., 2006; Schechenr
et al., 2001) or multiple images taken from foggy
scenes with different densities at the same point
(Narasimhan & Nayar, 2003a; Narasimhan & Nayar,
2003c). However, requirements of the specific
inputs make them impractical, particularly in real-
time applications. To overcome the drawbacks, a
method using a single input image has been
proposed to enhance the visibility of an image (Tan,
2007; Tan, 2008). This method shows compelling
results. However, it is computational expensive and
also causes evident color distortion.
Land proposed the Retinex theory based on
lightness and color constancy. Because of its
advantages such as dynamic range compression,
color independence and color and lightness rendition,
the Retinex theory has been extensively used in
image processing task. Among Land’s algorithms,
the center/surround Retinex (Land, 1986) attracts
researchers’ interests because of lower
computational complexity and no calibration for
scenes.
Based on the Retinex theory, we propose a novel
color-preserving defog method for foggy or hazy
scenes. In the proposed method, we estimate the
illumination by applying two-step smoothing to the
degraded image and then enhance contrast by
69
Xu D., Xiao C. and Yu J.
COLOR-PRESERVING DEFOG METHOD FOR FOGGY OR HAZY SCENES.
DOI: 10.5220/0001776200690073
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications (VISIGRAPP 2009), page
ISBN: 978-989-8111-69-2
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
applying adaptive contrast stretching to the
reflectance estimate. This method can achieve fog
removal and color restoration simultaneously for
foggy or hazy images. It has three advantages as
follows: 1) No user interactions; 2) A single image
as an input; 3) High efficiency. The rest of the paper
is organized as follows: Section 2 introduces the
Retinex theory; Section 3 analyzes the Retinex
theory from a new viewpoint and details the
proposed approach; Experiments are provided in
Section 4.
2 RETINEX
Let
()
,
I
xy be a digital image. According to the
Retinex theory,
()
,
I
xy is the product of the object
reflectance
()
,Rxy
and the scene illumination
()
,Lxy
, that is,
() ()()
,,,
I
xy RxyLxy=
(1)
where the object reflectance
()
,Rxy
represents
intrinsic properties of object surface, and the scene
illumination
()
,Lxy
determines dynamic range
compression of pixels. The goal of the Retinex
theory is to obtain the reflectance image
(
)
,Rxy
from input image
()
,
I
xy by removing effects of
illumination image
()
,Lxy
.
In the logarithmic domain, Equation (1) can be
written as
() () ()()
() ()
()()
,log,log , ,
log , log ,
,,
ixy Ixy RxyLxy
Rxy Lxy
rxy lxy
==
⎡⎤
⎣⎦
=+
=+
(2)
where
logrR= , loglL= . Although various
Retinex algorithms have different processes, they
usually include two mutual steps. Firstly, the input
image is converted to the logarithmic domain, which
is described in Equation (2). Secondly, the
illumination image is estimated by different
algorithms. Then the reflectance image is computed
by subtracting the illumination image from the
original image. The output is the reflectance image.
3 DEFOG
3.1 Method
In this section, we explain the Retinex theory from a
new viewpoint and apply it to remove fog/haze
effects from degraded images. Our method is
available for color images because gray images have
no color information. The main idea of our
explanation is described as follows. First of all, the
illumination is estimated. Then, the input image is
divided by the estimated illumination
()
,Lxy
%
to get
an estimate of the reflectance
()
,Rxy
%
, such that
(
)
(
)( )
,,,
R
xy I xy Lxy=
%%
(3)
To avoid the division computation, we convert the
operation to the logarithmic domain. Suppose that
we define
(
)
(
)
() ()
,ln,
ln , ln ,
rxy Rxy
Ixy Lxy
=
=−
%
%
%
(4)
In this way, we obtain the logarithm of the
reflectance by subtracting the logarithm of the
illumination from the logarithm of the degraded
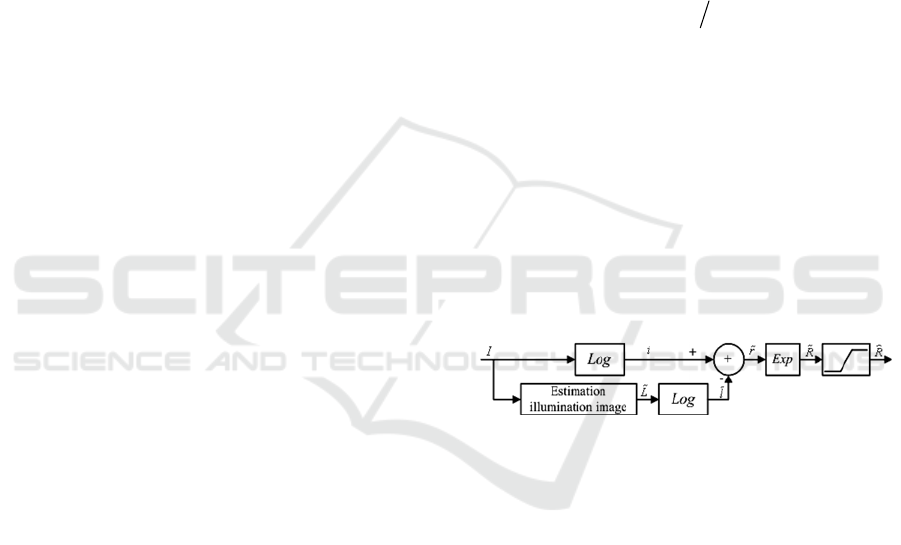
image. This flowchart of our method is depicted in
Figure 1.
Figure 1: Flowchart of our method.
3.2 Fog/ Haze Estimation
The key of our method is how to estimate the
illumination, that is, fog/haze for foggy/hazy images.
The illumination component of an image is generally
characterized by slow spatial variations, while the
reflectance component tends to vary abruptly. These
characteristics lead to associating the low
frequencies of an image with illumination and the
high frequencies with reflectance. The proposed
method is based on channel-to-channel processing.
Define
(
)
,
F
xy
to be zero-mean Gaussian with
standard derivation
σ
, which is a typical low-pass
smoothing function. Firstly, the degraded image is
convoluted with the smoothing function, that is,
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
70

(
)
(
)
(
)
ˆ
,,,
L
xy I xy F xy=∗
(5)
where “
∗
” denotes the convolution operation, and
(
)
,
F
xy
is the smoothing function and given by
()
22 2
()/
,
xy
Fxy Ke
σ
−+
=
(6)
where K is normalized factor and makes the
coefficients sum to 1,
σ
is standard deviation and
controls the degree of blurring. Specifically speaking,
assuming that the function has a
ww×
support, we
determine K satisfying with
()
()
(
)
()
(
)
12 12
12 12
,1
ww
xw yw
Fxy
−−
=− − =− −
=
∑∑
(7)
According to
3
σ
rule, the relationship between
σ
and w is given by
()
312w
σ
=−
(8)
Next, for
()
,
x
y∀
, the illumination estimate
()
,
L
xy
%
is obtained by computing the mean of
ˆ
L
,
meaning that the degraded image is smoothed for the
second time.
() ()
11
1
ˆ
,,
HW
xy
Lxy Lxy
HW
==
=
∑∑
%
(9)
And then, the reflectance is given by
() () ()
,ln,ln,rxy Ixy Lxy=−
%
%
(10)
At last, exponential transformation is indispensable
and used for contrast enhancement and dynamic
range stretching.
() ()
(
)
,exp,
R
xy r xy=
%
%
(11)
Figures 2(a)~(c) illustrate the process described
above. Figure 2(a) shows the original image. Figures
2(b) and 2(c) illustrate the fog/haze estimate and the
reflectance estimate, respectively.
3.3 Adaptive Contrast Stretching
The lower pixel values degrade the visibility of
the Retinex output. To overcome the problem,
we first find the lowest and highest pixel values,
low
T
and
high
T
, currently present in the image, and
then scale each pixel
k
I
such that
()
oklow
high low
ba
IaIT
TT
−
=+ −
−
(12)
where a and b are the lower and upper limits,
respectively. A single outlying pixel with a very
high or a very low value can severely affect the
value
low
T
and
high
T
, which leads to very undesirable
scaling. Therefore, we propose an adaptive method
to select the two thresholds according to a
cumulative distribution function (CDF) as follows.
(
)()()
(
)
1
arg ,
m
low m m m
I
TCIThCICI
−
=≥>
(
)
(
)
(
)
(
)
1
arg 1 ,
m
high m m m
I
TCIThCICI
−
=≥−>
(13)
where
(
)
m
CI is the cumulative histogram of R
%
. We
define a probability
Th
to determine
low
T
and
high
T
for preventing outliers from affecting the scaling.
For color images, all the channels will be stretched
using the same
low
T
and
high
T
in order to preserve the
correct color ratios. Figure 2(d) illustrates the final
result of adaptive contrast stretching.
4 SIMULATIONS
All experiments are implemented on a computer
with P4 3.0GHz, 1GB memory and MATLAB
development environment. The images with
haze/dense fog are provided to demonstrate the
feasibility and efficacy of the proposed method. The
performance is evaluated by subjective criterion
including visibility enhancement and color rendition.
Empirically, we select the standard deviation as
5
σ
=
. The two thresholds
low
T
and
high
T
are
calculated in term of
0.02Th =
.Figure 3(a) shows
Beijing University of Technology Olympic
Gymnasium involved in a haze and the visibility of
the gymnasium is degraded severely by the haze.
Figure 3(b) is the result of our method. As can be
observed, the gymnasium gets rid of the awful haze
and looks more magnificent. Figures 4(a) and 5(a)
are two snapshots of the movie “The mist” covered
with fog. As shown in Figure 4(b), more details of
the scene are recovered obviously. Seen from
Figure 5(a), the back of a man looms through the
dense fog, while in Figure 5(b), the dense fog is
cleared and the man appears distinct. Besides, the
color of clear-day counterparts recurs to our method.
We implement our method 10 times and calculate
the average time for each image. Table 1 lists the
computation time for the images of various sizes,
which shows our method has fast implementation.
We compare our method with Tan’s (Tan, 2007;
COLOR-PRESERVING DEFOG METHOD
FOR FOGGY OR HAZY SCENES
71

(a) Original foggy image.
(b) Fog/haze estimate.
(c) The reflectance estimate.
(d) Final result of adaptive contrast stretching.
Figure 2: Illustration of our method.
Tan, 2008). Figures 6 (a) and 6 (b) illustrate results
of Tan’s method and the proposed method,
respectively. The original image shown in Figure 6(a)
is covered with dense fog. The result of Tan’s
method achieves good visibility, but produces
evident color distortion, leading to severe artifacts.
As shown in Figure 6(b), the sky takes on bright, the
water dark green, and the boundary between them is
distinct. It’s obvious that the proposed method
greatly improves the visibility without color
distortion. The average computation time of the
proposed method is 3.515 seconds for the image of
size 443×594. More compelling results appear in
Tan’s method (Tan, 2008). However, there are more
severe color distortions and the computation time
approximates to 5 to 7 minutes for images of size
400×600.
Table 1: Computation time for various image sizes.
Figure 5 Figure 6 Figure 7
Time(s) 2.109 3.765 3.907
Size 319×500 398×718 408×719
5 CONCLUSIONS
We have proposed a novel color-preserving defog
method for foggy or hazy scenes. Experiment results
show that the improvement in image quality can be
achieved by the proposed method. Also, the method
has high-efficiency implementation.
REFERENCES
Kim J. Y., Kim L. S. and Hwang S. H. (2002). An
advanced contrast enhancement using partially
overlapped sub-block histogram equalization. IEEE
Trans. on Circuits and Systems for Video Technology,
11(4): 475-484.
Land E. (1998). An alternative technique for the
computation of the designator in the retinex theory of
color vision. In: Proceedings of National Academy of
Sciences, 83: 3078-3080.
Narasimhan S. and Nayar S. K. (2003a). Contrast
restoration of weather degraded images. IEEE Trans.
on PAMI, 25(6): 713-724.
Narasimhan S. and Nayar S. K. (2003b). Interactive (De)
weathering of an image using physical models. In:
Proceedings of ICCV Workshop on Color and
Photometric Method in Computer Vision, 25(6): 713-
723.
Narasimhan S. and Nayar S. K. (2003c). Shedding light on
the weather. In: Proceedings of IEEE CVPR, 1: 665-
672.
Schechenr Y. Y., Narasimhan S. G. and Nayar S. K.
(2001). Instant dehazing of images using polarization.
In: Proceedings of IEEE CVPR, 1: 325-332.
Shwartz S., Namer E. and Schechner Y. (2006). Blind
haze separation. In: Proceedings of IEEE CVPR, 2:
1984-1991.
Stark J. A. (2001). Adaptive image contrast enhancement
using generalizations ofhistogram equalization. IEEE
Trans. on Image processing, 9(5): 889-896.
Tan R.T. (2007). Visibility enhancement for roads with
foggy or hazy scenes. In: Proceedings of the IEEE
Intelligent Vehicles Symposium, 19-24.
Tan R.T. (2008). Visibility in bad weather from a single
image. In: Proceedings of IEEE CVPR, 1-8.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
72

(a) Original image covered by haze. (b) Defog result of (a).
Figure 3: Beijing University of Technology Olympic Gymnasium (Size: 319×500).
(a) Original image covered by fog. (b) Defog result of (a).
Figure 4: Snapshot 1 of Movie “The Mist” (Size: 398×718).
(a) Original image covered by dense fog. (b) Defog result of (a).
Figure 5: Snapshot 2 of Movie “The Mist” (Size: 408×719).
(a) Tan’s method. (b) Our method.
Figure 6: Comparison between Tan’s method and our method (Size: 443×594).
COLOR-PRESERVING DEFOG METHOD
FOR FOGGY OR HAZY SCENES
73
