THE ICA APPROACH FOR REMOVAL OF UNDESIRED
COMPONENTS FROM EEG DATA
Joanna Górecka
Institute of Control Engineering, Technical University of Szczecin, 26 kwietnia, Szczecin, Poland
Keywords: Independent Component Analysis, Blind Signal Separation, EEG data, Artifacts.
Abstract: The aim of this results of research is to detect and remove selected undesired signals by means of ICA
approach. In this paper have been presented the following algorithms BSS: HJ, Infomax and FastICA for
separation and removal of selected group of artifacts (eye blinks, muscle activity) from EEG recordings. As
it has been proven in experiments, the proposed algorithms can effectively detect and remove these artifacts
from EEG recordings.
1 INTRODUCTION
The Electroencephalogram is a biological signal that
represents the electrical activity of the brain. EEG
signals recorded at the scalp are mixtures of the
signals from multiple intra - and extracranial
sources. The assumption of independence of the
sources was justified through the successful
application of the ICA technique to the identification
and extraction of selected artifacts in EEG
recordings, as presented in (Cichocki, Amari, 2002).
In many cases a linear model is usually
inappropriate for EEG signals (Girolami, 2000).
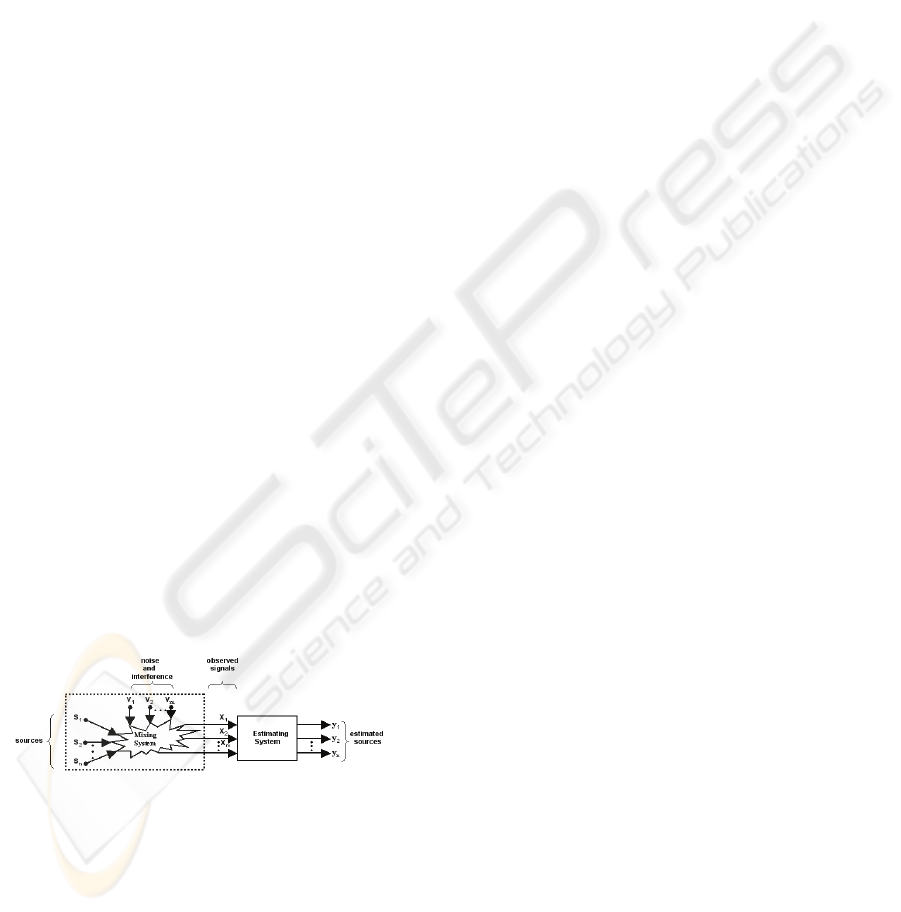
An important application of ICA is in Blind
Signal Separation. The block diagram illustrating
blind separation problem is presented in Figure 1.
Figure 1: General scheme of the blind separation process
(Cichocki, Amari, 2002).
Usually, in blind signal processing m mixed
signals
)(x t
i
for
mi ,...,2,1=
are linear combinations
of n mutually unknown and statistically independent
and zero-mean source signals
)(s t
j
for
nj ,...,2,1
=
and are noise - contaminated (Cichocki, Amari,
2002). It can be written in the matrix notation:
)v()s()x( ttt
+
=
H
(1)
where:
T
)](x,...,)(x,)([x)x( tttt
m21
=
- is a vector of
observed signals,
nm×
∈
R
H
- is an unknown mixing
matrix,
T
)](s,...,)(s,)([s)s( tttt
n21
=
- is a vector of signal
sources and
T
)](v,...,)(v,)([v)v( tttt
m21
=
- is a vector of
additive noise. On the other hand, the demixing
model is a linear transformation in the following
form:
)x()y( tt W
=
(2)
where:
T
)](y,...,)(y,)([y)y( tttt
n21
=
- is an estimate of
source signals
)s(t
and
nxm
RW ∈
- is a separating
matrix to be determined.
The aim of BSS using ICA is to estimate an
unmixing (separating) matrix such that
WXY
=
approximates the independent source signals as good
as possible (Roberts, Everson, 2001). In this paper,
the unmixing matrix for the instantaneous case is
equal to the inverse of the mixing matrix, i.e.
1−
= HW .
2 ADAPTIVE ALGORITHMS FOR
NON-STATIONARY SIGNALS
The choice of adaptive algorithm depends on the
statistical properties of sources and the specific
applications. For separation of independent and non-
gaussian signals, for example: EEG recordings, the
539
Górecka J. (2009).
THE ICA APPROACH FOR REMOVAL OF UNDESIRED COMPONENTS FROM EEG DATA.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 539-542
DOI: 10.5220/0001777605390542
Copyright
c
SciTePress

best performance can by achieved by using the
higher-order statistics (HOS) approach. In many
applications, separation algorithms are combinations
of two approaches: HOS and SOS. The second-order
statistics (SOS) are useful for blind signal
separation, when the source signals are statistically
non-stationary.
The fundamental restriction in ICA methods is
that independent components must be non-gaussian
for ICA to be as much as possible. The classical
measure of nongaussianity is kurtosis or the fourth-
order cumulant (Cichocki, Amari, 2002). A second
measure is given by negentropy, which is based on
the information - theoretic quantity of (differential)
entropy. Next approach for ICA separation is based
on information theory - minimization of mutual
information (Van Hulle, 2008).
Usually, algorithms for Independent Component
Analysis can be divided into two categories
(Cichocki, Amari, 2002). In the first category
algorithms rely on batch computations minimizing
or maximizing some relevant criterion functions, for
example: FOBI (Fourth Order Blind Identification),
FOBI-E (Fourth Order Blind Identification with
Transformation matrix E), JADE (Joint
Approximate Diagonalization of Eigen matrices),
JADE TD (Joint Approximate Diagonalization of
Eigen matrices with Time Delays), FPICA (Fixed-
Point ICA). It was a problem with these algorithms,
because they require very complex matrix or
tensorial operations.
In the second category adaptive algorithms often
based on stochastic gradient methods, for example:
NG-FICA (Natural Gradient - Flexible ICA),
ERICA (Equivariant Robust ICA - based on
Cumulants), SANG (Self Adaptive Natural Gradient
algorithm with nonholonomic constraints). The main
problem of these algorithms is the slow convergence
and dependence on the correct choice of the learning
rate parameters (in neutral networks). It has been
proven (Cichocki, Amari, 2002) that the Natural
Gradient algorithms improves greatly the learning
efficiency in blind separation process.
Generally, the adaptive learning algorithms can
by written in the general form by using estimating
functions (Cichocki, Amari, 2002):
ΔWWW +=+ )()1( tt
(3)
where:
)(tW
- is a separating matrix;
)())(( tt
fy
WRIΔW −=
μ
for that:
)(t
μ
- is a learning
rate at time,
I - is an identity matrix and
fy
R - is a
covariance matrix.
Many methods have been proposed to remove
eye blinks and muscle activity from EEG recordings
(Rangayyan, 2002; Sanei, Chambers, 2007).
Applications of ICA approach to EEG data have
concentrated on source localization and on artifacts
removal. Usually, the EEG recordings can be first
decomposed into useful signal and undesired
subspace of components using standard techniques
like local and robust PCA, SVD or nonlinear
adaptive filtering (Rangayyan, 2002). In the
following step, the ICA algorithms decomposed the
observed signals (signal subspace) into independent
components. It is worth to noting, that some useful
sources are not necessarily statistically independent.
Therefore, the perfect separation of primary sources
by using any ICA procedure cannot be achieved
(Roberts, Everson, 2001). However, in this
experiment the separation of the EEGs is not
important, but only the removal of independent
undesired components.
3 METHODS AND MATERIALS
The performance of three chosen adaptive
algorithms presented in this paper have been
implemented in MATLAB software.
Figure 2: Artifacts: a) eye blinks (1÷2,5) Hz; b) muscle
(20
÷60) Hz.
Figure 3: An example of EEG data with eye blinks and
muscle artifacts.
The EEG signals have been prepared using
BIOSIG (http://biosig.sourceforge.net/index.html),
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
540

EEGLAB (http://sccn.ucsd.edu/eeglab/)
and
ICALAB software (Cichocki et al., 2007).
For verification of the quality of separation and
removal of selected artifacts from EEGs, well-
known source signals have been artificially mixed
using well-known full rank mixing matrix (BSS
problem). Furthermore it has been assumed, that the
number of sources is equal to the number of sensors.
In the following step, two types of artifacts have
been added to appropriate channels: (T3, T4, T6,
O2) - muscle artifacts; (F3, F4) - eye blinks
(Majkowski, 1986). All signals were mixed using
the mixing matrix H (
7546,68)Hdet( =
).
Finally, three adaptive learning algorithms have
been chosen: HJ (Herault, Jutten, 1991), Infomax
(Bell, Sejnowski, 1995) and FastICA (Hyvärinen,
1999).
In the HJ algorithm non-gaussian sources with
similar number of independent sources and mixtures
have been considered. A solution based on a
recurrent artificial neural network for separation of
these sources has been proposed. It can be written
as:
))(())(()( ttt
dt
d
yhyg
W
η
=
(4)
where:
)(t
η
- is a learning rate, )(⋅g and
)(
⋅
h
- are
the different nonlinear odd functions,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
0...
............
...0
...0
21
221
112
nn
n
n
ww
ww
ww
W
. For the simulations the
following parameters have been used:
2000)(
0
=t
η
,
3
)( xxg =
and
)()( xarctgxh =
.
In the next algorithm Infomax it has been shown
that maximizing the joint entropy
)(YH
, of the
output of a neural processor minimizes the mutual
information among the output components,
)(
ii
ugy =
, where
)(
i
ug
is an invertible bounded
nonlinearity and
Wxu =
. For EEG recordings the
learning rule can be represented in the following
form:
WuyIWW
W
YH
W )
ˆ
(
)(
TT
+=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−=Δ
μμ
(5)
where:
01,0=
μ
,
i
u
i
ug
−
+
=
e1
1
)(
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
i
i
i
u
y
ln
u
y
ˆ
have been used for simulations.
The third adaptive algorithm - FastICA is a
fixed-point algorithm that can be used for estimating
the independent components one by one. This
algorithm finds one of the columns of the separating
matrix and so identifies one independent source
within signal duration (Hyvärinen, 1999).
The corresponding
independent source signal
can be found using the following equation:
)()(
ˆ
kk
T
vWs =
(6)
where:
V
- is a whitening matrix given by
T
UΛV
2
1
−
=
,
[
]
)(),...,1(diag m
λ
λ
=
Λ
- is a diagonal
matrix with the eigenvalues of the data covariance
matrix
{
}
T
kkE )()( xx
, U - is a matrix with the
corresponding eigenvectors as its columns. Each lth
iteration of this adaptive algorithm is defined as:
(
)
{
}
1
3
1
3*
−−
−=
l
T
ll
E wvwvw
;
lll
** www =
(7)
4 RESULTS
The results of comparisons of three selected
algorithms are presented below. Figure 4 shows a 2-
sec interval of an EEG time series and ‘corrected’
EEG signals obtained by removing selected artifacts
using different adaptive algorithms.
Figure 4: Plots illustrating EEG recordings: a) a set of
normal EEG signals affected by the artifacts: eye blinks
and muscle activity and the EEG signals after removal of
these artifacts using the following algorithms: b) HJ, c)
Infomax , d) FastICA.
The algorithms are compared using the
coefficient ε - the difference between an estimate of
source signals
)(y t
n
and original EEG signals
)(s t
n
(without artifacts) defined for different channels in
a) b) c) d)
THE ICA APPROACH FOR REMOVAL OF UNDESIRED COMPONENTS FROM EEG DATA
541

the following form:
[]
∑
=
=
m
n
nnn
ttt
1
)(s-)(y)(ε
(8)
For ideal case, when the perfect removal is
achieved, the coefficient ε is zero. In these
simulations any
of the presented adaptive algorithms
cannot remove all artifacts, but only minimizes their
influence on desired EEG signals.
Below, it is presented how error quantity
depends on the type of adaptive algorithm and the
type of channel.
Figure 5: Plots illustrating error signals ε versus time
function for eye blinks: a) HJ, b) Infomax, c) FastICA.
Figure 6: Plots illustrating error signals ε versus time
function for muscle activity: a) HJ, b) Infomax, c)
FastICA.
5 CONCLUSIONS
The paper presents selected adaptive algorithms and
compares the performance of three separation
algorithms of the EEG signals in the presence of two
types of artifacts.
Biomedical source signals are usually distorted
by different artifacts. Besides classical signal
analysis tools (such as adaptive supervised filtering,
parametric or non-parametric spectral estimation,
time-frequency analysis) the proposed ICA approach
can be used for detection and reduction of artifacts
from EEG recordings.
During tests, it has been observed that the
proposed adaptive algorithms can effectively detect
and remove these selected artifacts, but their
effectiveness depends on the type of artifact and on
the type of channel (Figure 5, Figure 6).
ACKNOWLEDGEMENTS
This work is supported by MNiSW (of Government
Administration in Poland) - Grant no. N N518
335035 (2008÷2010).
REFERENCES
Bell A. J., Sejnowski T. J., 1995. An information -
maximization approach to blind separation and blind
deconvolution. Neural Computation, 7:1129-1159.
Cichocki A., Amari S., 2002. Adaptive Blind Signal and
Image Processing: Learning Algorithms and
Applications, Wiley, England.
Cichocki A., Amari S., Siwek K., Tanaka T., Phan H.,
2007. http://www.bsp.brain.riken.jp/ICALAB.
Girolami M., 2000. Advances In Independent Component
Analysis, Springer, London.
Hyvärinen A., 1999. Fast and Robust Fixed-Point
Algorithms for Independent Component Analysis.
IEEE Transactions on Neural Networks 10(3):626-
634.
Jutten C., Herault J., 1991. Blind separation of sources,
Part I: An adaptive algorithm based on neuromimetic
architecture. Signal Processing, 24:1-10.
Majkowski J., 1986. Elektroencefalografia kliniczna,
Państwowy Zakład Wydawnictw Lekarskich,
Warszawa.
Rangayyan R. M., 2002. Biomedical Signal Analysis,
Wiley, New York.
Roberts S., Everson R., 2001. Independent Component
Analysis: Principles and Practice, Cambridge
University Press.
Sanei S., Chambers J. A., 2007. EEG Signal Processing,
Wiley, Cardiff.
Van Hulle M., 2008. Sequential Fixed-Point ICA Based
on Mutual Information Minimization. Neural
Computation, Vol. 20, No. 5: 1344–1365.
a) b) c)
a) b) c)
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
542
