A MULTISCALE OPERATOR FOR DOCUMENT IMAGE

BINARIZATION

Leyza Baldo Dorini and Neucimar Jer

onimo Leite

Institute of Computing, P.O.Box: 6176, University of Campinas - UNICAMP, 13084-971, Campinas, SP, Brazil

Keywords:

Scale-space, Document binarization, Image analysis.

Abstract:

Basically, document image binarization consists on the segmentation of scanned gray level images into text

and background, and is a basic preprocessing stage in many image analysis systems. It is essential to threshold

the document image reliably in order to extract useful information and make further processing such as char-

acter recognition and feature extraction. The main difﬁculties arise when dealing with poor quality document

images, containing nonuniform illumination, shadows and smudge, for example. This paper presents an ef-

ﬁcient morphological-based document image binarization technique that is able to cope with these problems.

We evaluate the proposed approach for different classes of images, such as historical and machine-printed

documents, obtaining promising results.

1 INTRODUCTION

Document image binarization converts gray-scale im-

ages into binaries ones which are more appropriate to

be used in several image analysis and understanding

systems. Also, due to the increasing number of doc-

uments being digitalized, binarization has been used

to facilitate data management and decrease storage

space requirements.

Since the accuracy of the resulting images

strongly affects the performance of subsequent high

level tasks, such as optical character recognition

(OCR) and feature extraction, it is essential to ﬁnd

thresholding methods that correctly keep all useful in-

formation while removing background and undesired

details corresponding to noise.

The main difﬁculties in this sense arise from the

fact that document images can be subjected to differ-

ent degradation problems, which can signiﬁcantly dis-

turb the results if appropriate methods are not used.

These problems may occur due to several reasons,

like aging and environmental conditions. In histori-

cal document images, for example, it is very common

to have seepage of ink, uneven illumination, smear

and smudge. When working with scanned images, the

main difﬁculties are related to poor printing/writing

quality and low contrast due to shadows.

In this paper, we propose a multiscale binariza-

tion algorithm that explores the simpliﬁcation prop-

erties of a scale-space toggle operator to deﬁne a dy-

namic thresholding operation. In contrast to other ap-

proaches, image maxima and minima interact at the

same time, conducing to a region merging that sim-

pliﬁes the image in such a way that important image

structures can be identiﬁed even in ill-illuminated im-

ages. The binarization rule depends on the local con-

vergence of a pixel to a signiﬁcative extrema, thus tak-

ing into account the whole image structure, and not

only the local gray level. In a few words, if a pixel

converges to a local minima, it is set to black. Other-

wise, it is set to white.

To assess the robustness of our approach, we com-

pare it against known threshold-based segmentation

methods using images of different classes and sub-

jected to different degradation problems. As we will

se elsewhere, our approach is computationally efﬁ-

cient and conduce to better results for a wide range

of experiments.

Section 2 brieﬂy reviews some image threshold-

ing techniques and Section 3 describes the proposed

approach. Section 4 presents the experimental re-

sults and Section 5 draws some conclusions and fu-

ture work perspectives.

2 RELATED WORK

Document image binarization approaches are typi-

cally classiﬁed into global and local methods. The

former are based on histogram analysis, with the

JerÃt’nimo Leite N. and Baldo Dorini L.

A MULTISCALE OPERATOR FOR DOCUMENT IMAGE BINARIZATION.

DOI: 10.5220/0001779000340039

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications (VISIGRAPP 2009), page

ISBN: 978-989-8111-69-2

threshold value being determined based on the mea-

sure that best separate the histogram peaks. However,

not necessarily all features of interest form promi-

nent peaks. In a general way, global approaches yield

good results only when there is a good separation

between foreground and background, a limitation in

document images with degradation problems like in-

homogeneous backgrounds, smears and strains.

A well-known general purpose histogram-based

global thresholding approach is the Otsu’s algo-

rithm (Otsu, 1979). Brieﬂy, it selects as an opti-

mal threshold the one which minimizes the ratio be-

tween the “between-class” and the total variance. The

between-class variance is deﬁned as the deviation

of the mean values for each considered class (back-

ground and object) from the overall mean of the pix-

els.

On the other hand, local thresholding approaches

provide an adaptive solution where the threshold

value is determined pixelwise and depends on re-

gional image characteristics. Due to the computa-

tional cost, it is important to deﬁne efﬁcient transfor-

mations to be applied locally. We have compared our

approach against some of these methods, described

below.

The moving averages method considers a thresh-

old based on the mean gray level of the last n pixels,

and it is designed for images containing text. The im-

age can be treated as a one-dimensional stream of pix-

els and the average can either be computed exactly or

estimated via (Parker, 1996):

i+1

= M

−

+ g

i+1

(1)

where M

i+1

is the estimate of the moving average for

pixel i + 1 having gray level g

i+1

and M

is the previ-

ous moving average (i.e. for pixel i). Any pixel less

than a ﬁxed percentage of its moving average is set to

black; otherwise it is set to white.

The Niblack’s algorithm deﬁnes a local threshold

based on the mean and standard deviation values cal-

culated over a rectangular window around the pixel

according to the following formula (Niblack, 1986):

T = m + k ∗ s (2)

where m is the mean and s the standard deviation of

the pixels in the window. The variable k determines

how much of the object is retained, and assumes a

value between −1 and 1. As drawbacks, we have the

low thresholding speed, the sensitivity to the size of

the window and the occurrence of noise in the back-

ground.

In order to minimize the background noise in im-

ages with uneven illumination, Sauvola proposed an

extension to Niblack’s algorithm where the threshold

value is computed with the dynamic range of the stan-

dard deviation, R, according to the equation (Sauvola

and Pietikainen, 2000):

T = m ∗



1 + k



− 1



(3)

where, again, m and s are mean and standard devi-

ation of the window. Here, k takes a positive value

between 0 and 1. To properly determine the R value,

it is necessary to know the document contrast. The

inﬂuence of the window size and the threshold speed

still remain a problem.

Gatos et al. (Gatos et al., 2006) proposed a locally

adaptative binarization scheme that can deal with de-

graded document images. The method consists in ﬁve

basic steps, starting from a rough estimation of the

foreground, obtained using the Sauvola’s algorithm,

that is improved using local image analysis. More

complete reviews of image thresholding techniques

can be found in (Trier and Jain, 1995) (Gatos et al.,

2006) (Sahoo et al., 1988) (Sezgin and Sankur, 2004).

3 SCALE-SPACE TOGGLE

OPERATOR FOR IMAGE

SIMPLIFICATION

Multiscale approaches have been largely consid-

ered, playing an important role when designing auto-

matic methods to cope with real world measurements

where, in most of the cases, there is no prior informa-

tion about which would be the appropriate scale.

Here, we use an operator based on the scale-space

approach (Witkin, 1984), in which the inherent mul-

tiscale nature of real-world images is represented by

embedding the original signal into a family of simpli-

ﬁed signals, created by successively removing image

structures across scales while preserving the essential

features. Since the representation of an interest sig-

nal feature describes a continuous path through the

scales, it is possible to relate information obtained in

different representation levels, a drawback in many

multiscale approaches.

Due to the problems inherent to the linear ap-

proaches (Witkin, 1984), non-linear scale-space oper-

ators based on mathematical morphology have been

frequently used (Bosworth and Acton, 2003). In

this context, scale-spaces are generated by ﬁltering

gray-scale signals with speciﬁc combinations of the

scaled erosion and dilation operations, deﬁned as fol-

lows (Jackway and Deriche, 1996).

Deﬁnition (Dilation). The dilation of the function

f (x) by the structuring function g

(x), ( f ⊕ g

)(x),

A MULTISCALE OPERATOR FOR DOCUMENT IMAGE BINARIZATION

is given by:

( f ⊕ g

)(x) = sup

t∈G∩D

{ f (x − t) + g

(t)} (4)

Deﬁnition (Erosion). The erosion of the function

f (x) by the structuring function g

(x), ( f  g)(x), is

given by:

( f  g

)(x) = inf

t∈G∩D

{ f (x + t) − g

(t)} (5)

where f : D ⊂ R

→ R is the image function, D

the translate of D, D

= {x +t : t ∈ D}, and g

: G

⊂

→ R is the scaled structuring function

(x) = |σ|g(|σ|

−1

x) x ∈ G

, ∀ σ 6= 0. (6)

To ensure reasonable scaling behavior, g

must be a

monotonic decreasing function along any radial di-

rection from the origin (i.e., anti-convex). To avoid

level-shifting and horizontal translation effects, re-

spectively, one must also observe the conditions

sup

t∈G

(t)} = 0 and g

(0) = 0. (7)

We use a scale-space toggle operator, named

Self-dual Multiscale Morphological Toggle

(SMMT) (Dorini and Leite, 2008), which uses

as primitives iterated versions of an extensive and

an anti-extensive transformation, namely, the scale

dependent dilation and erosion deﬁned above. The

decision rule is based on which primitive value is

closer to the original one.

Deﬁnition (Self-dual Multiscale Morphological

Toggle Operator). Let the primitives be deﬁned as

(x) = ( f ⊕ g

)

(x) and φ

(x) = ( f  g

)

(x), that

is, the dilation and erosion, respectively, of f (x) with

the scaled structuring function g

n times. The Self-

dual Multiscale Morphological Toggle (SMMT) op-

erator is deﬁned as (Dorini and Leite, 2008):

( f  g

)

(x) =







(x), if φ

(x) − f (x) < f (x) − φ

(x),

f (x), if φ

(x) − f (x) = f (x) − φ

(x),

(x), otherwise.

(8)

Idempotence is usually desired when dealing with

toggle-like transformations to avoid undesirable ef-

fects, such as oscillations (Serra and Vicent, 1992).

Since the previously deﬁned operator is not idem-

potent, it is important to ensure that it has a well-

controlled behavior for any parameter set.

It has been proved that the operator obeys the nec-

essary conditions to constitute a scale-space opera-

tor for varying scale (Dorini and Leite, 2007). The

monotonicity property (requiring that the number of

features must necessarily be a monotonic decreas-

ing function of scale) holds when using as features

image extrema (there is no need to consider image

maxima and minima separately as in previous ap-

proaches (Jackway and Deriche, 1996)). The SMMT

operator has interesting characteristics, such as self-

duality, i.e., there is a symmetric treatment of fore-

ground and background, thus reducing the gray-level

bias. Also, it leads to an image simpliﬁcation that

does not displace the boundaries.

On the other hand, when considering iterative ap-

plications of the operator, a stronger simpliﬁcation is

obtained and regions are merged as discussed below.

To make calculations easier and more intuitive, let us

consider the pyramid structuring function given by

(x, y) = −|σ|

−1

max{|x|, |y|} (9)

in its scaled version. Under these conditions, we have

the following equivalence for the SMMT operator (for

a ﬁxed scale σ):

( f  g

)

(x) == ( f  g

2n+1

)

(x) (10)

where the subscript on σ denotes the structuring ele-

ment size. In a few words, n iterations of the primi-

tives using a 3 × 3 structuring element is equivalent

to one iteration using a structuring element of size

2n+1. Since the transformed value of a pixel depends

on the dominant extrema in the region being consid-

ered, the increasing on the number of iterations sim-

pliﬁes the image so that these extrema create wider

“attraction zones”, leading to a homogenization of

the gray levels. The deﬁned operator can be seen as

a quasi-connected operator, in the sense that it sim-

pliﬁes the image by creating quasi-ﬂat zones as ex-

plained next.

Deﬁnition (Maragos and Meyer, 2000) (R-ﬂat-

zone). Two pixels x, y belong to the same R-ﬂat zone

of a function f if and only if there exists an n-tuple

of pixels (p

, p

, . . . , p

) such that p

= x and p

= y,

and for all i, (p

, p

i+1

) are neighbors and satisfy the

symmetrical relation f

R f

i+1

In this paper, R corresponds to the relation |p

−

i+1

| ≤ λ. When R is the equality, we are dealing with

ﬂat zones, which consist on connected components

where the pixel value is constant. In Figure 1, we

show the transformation of the gray levels of a small

portion of an image when applying successive itera-

tions of the deﬁned operator, n = 1 . . . 5, with σ = 1.

Observe that quasi-ﬂat zones are created.

Here, we explore these properties to deﬁne a dy-

namic local thresholding operator as follows:

Deﬁnition (Binary Self-dual Multiscale Morpho-

logical Toggle Operator). Let the primitives be

deﬁned as φ

(x) = ( f ⊕ g

)

(x) and φ

(x) = ( f 

)

(x), that is, the dilation and erosion, respectively,

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

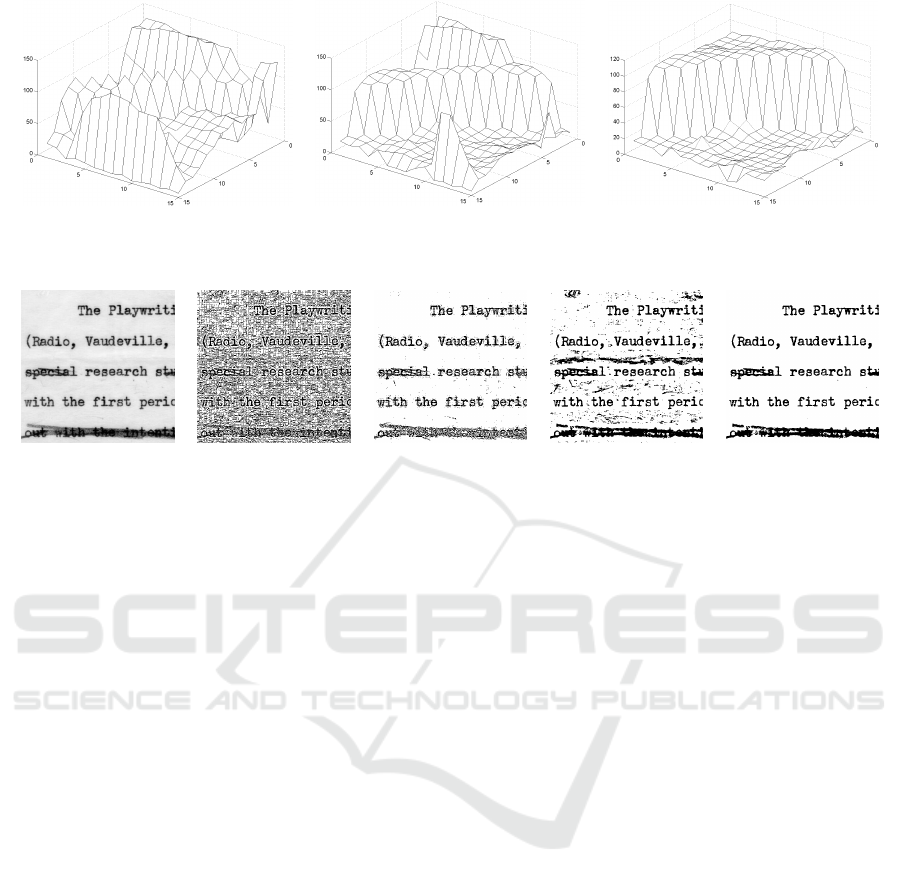
(a) (b) (c)

Figure 1: Simpliﬁcation obtained by considering successive iterations (1, 3 and 5) of the operator at scale σ = 1.

(a) (b) (c) (d) (e)

Figure 2: Inﬂuence of the scale and number of iterations parameters in the binarization. (a) original image and images

processed by the BSSMT operator using the parameters (b) σ

−1

= 1 and n = 1, (c) σ

−1

= 10 and n = 1, (d) σ

−1

= 1 and

n = 10 and (e) σ

−1

= 5 and n = 10.

of f (x) with the scaled structuring function g

times. We call Binary Self-dual Multiscale Morpho-

logical Toggle (BSMMT) operator:

( f  g

)

(x) =



255, if φ

(x) − f (x) <= f (x) − φ

(x),

0, otherwise,

(11)

Basically, if a pixel converges to a local maxima,

it is set to white. Otherwise, it is set to black. In

such a way, the thresholding depends on the the image

structures, and not only on the gray level in a pre-

deﬁned region.

Figure 2 illustrates how the parameters inﬂuence

the binarization results. When using σ = 1 and n = 1,

Figure 2(b), a great amount of noise remains in the

background. In a different scale, Figure 2(c), less fea-

tures persist, but the letters are noisy because the most

signiﬁcative image extrema inﬂuence only a small re-

gion. When considering more iterations, Figure 2(d),

we have the opposite situation (undesired features but

good letters’ deﬁnition). With an appropriate combi-

nation of the parameters a satisfactory segmentation

is obtained (Figure 2(e)).

4 EXPERIMENTAL RESULTS

We compare our approach against the binarization

methods discussed in Section 2 using degraded im-

ages of three different categories: historical handwrit-

ten documents, old newspapers and poor quality mod-

ern documents. In the following, we show an exam-

ple of each class and discuss the overall conclusions

about each method.

In a general way, the historical handwritten doc-

ument images of our test set have non-uniform illu-

mination, seepage of ink, shadows, smear and strain.

Additionally, old newspaper images have extra noise

mainly due to the old printing matrix precision. Fi-

nally, the modern documents have shadows that dif-

ﬁcult the separation between background and text.

Since no ground truth was available, we evaluate the

binarization results according to visual criteria such as

image quality and preservation of meaningful textual

information.

Figure 3 illustrates the binarization of an old

newspaper image. We compare our results against

the ones obtained by Niblack’s and Sauvola’s algo-

rithms, which has been implemented taking k = −0.2

and k = 0.5, respectively, as suggested in (Niblack,

1986) and (Sauvola and Pietikainen, 2000). We

use a 60 × 60 window (covering 1-2 characters) in

both cases. For Niblack’s algorithm, there is too

much noise in the background region, while Sauvola’s

method yields thin and broken characters in several

examples. Our approach presents accurate results.

Figure 4 shows an example of historical handwrit-

ten image. The approach suggested in (Gatos et al.,

2006) yields regular results, but the use of Sauvola’s

A MULTISCALE OPERATOR FOR DOCUMENT IMAGE BINARIZATION

(a) (b) (c) (d)

Figure 3: Binarization results. (a) original image, (b) Niblack, (c) Sauvola and (d) Our approach.

(a) (b) (c)

Figure 4: Binarization results. (a) original image, (b) Gatos et al. and (c) Our approach.

(a) (b) (c) (d) (e) (f)

Figure 5: Binarization results. (a) original image, (b) Otsu, (c) Moving Averages, (d) Niblack, (e) Sauvola and (f) Our

approach.

algorithm to obtain a ﬁrst rough approximation of the

foreground implies on a resulting image with broken

or even discarded characters. On the other hand, our

approach has shown to produce more reliable results,

presenting a superior performance even when the in-

put images are noisy and highly degraded.

The example of Figure 5 illustrates the robustness

of the BSSMT operator to images with uneven illu-

mination (Figure 5(a)). Observe in Figure 5(b) how a

global threshold method, such as Otsu’s, fails when

choosing a unique threshold for the whole image.

For the Niblack’s (Figure 5(d)) and Sauvola’s (Fig-

ure 5(e)) algorithms, the letters in the regions with a

brighter illumination were wrongly classiﬁed as back-

ground. The moving averages algorithm (Figure 5(c))

is less sensitive to the noise, but the resulting image

presents some white stripes in the letters, illustrated

in Figure 6(b), which can disturb the results when

performing an OCR system (Figure 7). As you can

see from Figures 5(f) and 7(c), the proposed approach

yields accurate results that can be properly used in the

same OCR software.

5 CONCLUSIONS

We have presented an adaptative document binariza-

tion technique for segmenting text from degraded

document images. We explore the scale-space proper-

ties of a toggle operator to deﬁne a new thresholding

operation that is robust to non-uniform illumination.

When using appropriate parameters, the SMMT oper-

ator leads to a meaningful region merging that simpli-

ﬁes the image, thus eliminating undesired details such

as noise. The binarization rule takes into account the

way image maxima and minima interact in this merg-

ing process to determine the value of each pixel.

When compared to other well-known approaches,

the proposed operator has shown to be robust to a

wide range of degradation problems, without yielding

extremely thinned and broken characters.

Since most document processing systems analyze

a large number of documents, having different styles

and layouts, it is important to develop automatic tech-

niques that do not require user intervention to set pa-

rameters each time it is applied. Thus, we will ex-

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

(a) (b)

Figure 6: (a) Our approach result and (b) The moving averages algorithm yields stripes that disturb the OCR results.

(a) (b) (c)

Figure 7: Results of an automatic OCR system using Abby software (ABBYY, 2008). (a) Original image, (b) using the

moving averages result (Figure 5(c)) and (c) using the result of our approach (Figure 5(f)).

tend our approach to use different representation lev-

els (scales) to extract the interest characters automat-

ically. Future work also includes the validation of the

method using quantitative measures.

ACKNOWLEDGEMENTS

The authors are grateful to FAPESP (07/52015-0;

05/04462-2) and MCT/CNPq (472402/2007-2) for

the ﬁnancial support of this work.

REFERENCES

ABBYY (2008). www.ﬁnereader.com.

Bosworth, J. and Acton, S. (2003). Morphological scale-

space in image processing. Digital Signal Processing,

13:338–367.

Dorini, L. E. B. and Leite, N. J. (2007). A scale-space tog-

gle operator for morphological segmentation. In 8th

International Symposium on Mathematical Morphol-

ogy, pages 101–112.

Dorini, L. E. B. and Leite, N. J. (2008). Multiscale im-

age representation using scale-space theory. In XXXI

Congresso Nacional de Matemtica Aplicada e Com-

putacional, pages 130–137.

Gatos, B., Pratikakis, I., and Perantonis, S. (2006). Adap-

tative degraded image binarization. Pattern Recogni-

tion, 39:317–327.

Jackway, P. T. and Deriche, M. (1996). Scale-space proper-

ties of the multiscale morphological dilation-erosion.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 18:38–51.

Maragos, P. and Meyer, F. (2000). A pde approach to

nonlinear image simpliﬁcation via levelings andrecon-

struction ﬁlters. In International Conference on Image

Processing, pages 938–941.

Niblack, W. (1986). An Introduction to Digital Image Pro-

cessing. Prentice Hall.

Otsu, N. (1979). A threshold selection method from grey-

level histograms. IEEE Transactions on Systems, Man

and Cybernetics, 9(1):377–393.

Parker, J. R. (1996). Algorithms for Image Processing and

Computer Vision. Wiley.

Sahoo, P., Soltani, S., and Wong, A. (1988). A survey of

thresholding techniques. Comput. Vision, Graphics

Image Processing, 41(2):233260.

Sauvola, J. and Pietikainen, M. (2000). Adaptive document

image binarization. Pattern Recognition, 33:225–236.

Serra, J. and Vicent, L. (1992). An overview of morpholog-

ical ﬁltering. Circuits, Systems and Signal Processing,

11(1):47–108.

Sezgin, M. and Sankur, B. (2004). Survey over image

thresholding techniques and quantitative performance

evaluation. J. Electron. Imaging, 13:146–165.

Trier, O. and Jain, A. (1995). Goal-directed evaluation of bi-

narization methods. IEEE Trans. Pattern Anal. Mach.

Intell., 17:1191–1201.

Witkin, A. P. (1984). Scale-space ﬁltering: a new approach

to multi-scale description. In Image Understanding,

pages 79–95. Ablex.

A MULTISCALE OPERATOR FOR DOCUMENT IMAGE BINARIZATION