
BRAIN ACTIVITY DETECTION
Statistical Analysis of fMRI Data
Alicia Quir
´
os Carretero and Raquel Montes Diez
Departamento de Estad
´
ıstica e Investigaci
´
on Operativa, Universidad Rey Juan Carlos, M
´
ostoles, Madrid, Spain
Keywords:
Bayesian inference, fMRI, Activity detection, GMRF.
Abstract:
We are concerned with modelling and analysing fMRI data. An fMRI experiment is a series of images obtained
over time under two different conditions, in which regions of activity are detected by observing differences
in blood magnetism due to hemodynamic response. In this paper we propose a spatiotemporal model for
detecting brain activity in fMRI. The model makes no assumptions about the shape or form of activated
areas, except that they emit higher signals in response to a stimulus than non-activated areas do, and that
they form connected regions. The Bayesian spatial prior distributions provide a framework for detecting
active regions much as a neurologist might; based on posterior evidence over a wide range of spatial scales,
simultaneously considering the level of the voxel magnitudes together with the size of the activated area.
A single spatiotemporal Bayesian model allows more information to be obtained about the corresponding
magnetic resonance study. Despite higher computational cost, a spatiotemporal model improves the inference
ability since it takes into account the uncertainty in both the spatial and the temporal dimension. A simulated
study is used to test the model applicability and sensitivity.
1 INTRODUCTION
Magnetic Resonance Imaging is a method used to vi-
sualise the inside of living organisms as well as to de-
tect the amount of bound water in geological struc-
tures. It does not require painful interventions and it
is a widely used tool in medical diagnosis support.
The fundamental research to develop magnetic reso-
nance imaging techniques started at the beginning of
XIX century although the image obtaining technology
could not be developed until the appearance of high
speed computers. The sensitivity of Magnetic Res-
onance to changes in blood oxygen level was discov-
ered at the beginning of the 80’s and this was the great
advance that caused the advent of functional Mag-
netic Resonance Imaging. As it was already known
that changes in blood flow and blood oxygenation
(collectively known as hemodynamics) in the brain
are closely linked to neural activity, fMRI could be
used from then on to track physiological activity. Im-
age acquisition with BOLD (Blood Oxygen Level De-
pendency) contrast is based on that principle (Ogawa
et al., 1990). Since 1990, fMRI has greatly increased
knowledge of the brain functions in neuroscience and,
in other fields, has contributed to a better understand-
ing of the physiology of different organs. Scientists
use fMRI to identify changes in the brain activity of
patients with certain pathologies in order to develop
new and more effective treatments and therapies. It
also serves as a guide to surgeons during operations
for the pain to be minimised.
To understand the fMRI acquisition process it
is necessary to understand the underlying physics
(Huang, 1999; Jezzard et al., 2001). Essentially, mag-
netic resonance machines build the image analysing
structural changes in an electromagnetic wave sent to
hydrogen atom protons in the different tissues of the
human body. The grey level of each voxel in the im-
age corresponds to the behaviour of a large number of
protons and it permits the identification of different
tissues through the definition of the image contrast.
Once generated, magnetic resonance images are
digitally treated to improve quality and to minimise
error sources that could bias future statistical analy-
434
Quirós Carretero A. and Montes Diez R. (2009).
BRAIN ACTIVITY DETECTION - Statistical Analysis of fMRI Data.
In Proceedings of the Inter national Conference on Bio-inspired Systems and Signal Processing, pages 434-439
DOI: 10.5220/0001781204340439
Copyright
c
SciTePress

sis. Image pre-processing steps are usually: realign-
ment, unwrapping, coregistering, slice timing correc-
tion, low-pass filtering, linear trend removal, smooth-
ing and normalisation. Statistical analysis is posterior
to pre-processing and its goal is to localise activity re-
gions in presence of noise. In a block-design fMRI
study, a large number of scans are obtained under dif-
ferent conditions (usually, rest and activity states) in
order to infer significative differences between them.
2 APPROACHES TO ANALYSIS
OF fMRI DATA
Inference regarding brain activity in fMRI data is
commonly addressed through the GLM analysis,
(Friston et al., 1995), in which a linear dependency
of the BOLD signal and the hemodynamic response
function (HRF) is assumed.
Generally, the stimulus pattern is fitted simply as
a box-shaped wave, slightly delayed, in order to ac-
count for the lapse of time between the stimulus onset
and the arrival of the blood to the activated area. This
box-shaped wave is convolved with a HRF template,
for which several kernels have been considered, in-
cluding Poisson (Friston et al., 1994), Gaussian (Fris-
ton et al., 1995) and gamma (Lange and Zeger, 1997).
The result of this analysis is a t, F or Z estimate for
each pixel. The next step is to threshold it (leading
to a multiple comparisons problem), in order to de-
cide, at a given level of significance, which parts of
the brain are activated. The convolution approach is
attractive for its simplicity. However, it imposes se-
vere restrictions on the model.
The most popular and complete statistical package
is SPM (Friston et al., 2006), created by (Frackowiak
et al., 2004). SPM is based on GLM. Some other au-
thors fit the HRF making use of GLM. As univariate
methods do not take into account the spatial structure
on data, they proposed a higher level spatial structure
modelisation (Bowman et al., 2008; Harrison et al.,
2007; Hartvig and Jensen, 2000; Gossl et al., 1999).
Multivariate methods provide an alternative to in-
dividual analysis of voxels, reducing the whole spa-
tiotemporal data set into certain multivariate compo-
nents with similar temporal characteristics. Multivari-
ate techniques applied to the analysis of fMRI data
include principal component analysis (Friston, 1994;
Sj
¨
ostrand et al., 2006), independent component analy-
sis (Beckmann and Smith, 2004; Esposito et al., 2003;
McKeown et al., 2003; Calhoun et al., 2001; Po-
rill et al., 1999) and cluster analysis (Goutte et al.,
1999). Interpretation of results must be treated with
care when using these techniques, as there is a high
risk of data overfitting.
In order to make use of more complex models
and to overcome the multiple comparisons problem,
the best choice is to work in a Bayesian framework,
which also allows including prior information on the
expected location, shape and size of the activation ar-
eas. Most Bayesian approaches to the modelling of
fMRI data use Markov random fields (MRF) as prior
distributions, in order to account for the spatial struc-
ture present in the data (Holmes, 1995; Gossl et al.,
2001; Woolrich et al., 2004b). An alternative to these
priors are, for example, Laplacian priors on regression
coefficients in GLM (Penny et al., 2005).
The fMRI data analysis is a problem that involves
the spatiotemporal relationship between a stimulus
or cognitive task and the cerebral response measured
with fMRI. In spite of the obvious spatiotemporal
nature of data, there are a few spatiotemporal mod-
els (Bowman, 2007; Katanoda et al., 2002; Woolrich
et al., 2004a), all of them based on convolution.
3 THE MODEL
We propose a spatiotemporal model to analyse fMRI
data in order to detect activity regions in the brain.
We extend (Quir
´
os et al., 2006), a fully Bayesian two-
stage model to localise activity regions in fMRI. In
the first stage, the observed HRF is fitted, pixelwise,
by a scaled and shifted Poisson distribution curve. A
map of values for the observed activity magnitude in
each pixel is obtained during this stage. The second
part consists of a spatial analysis of this map by the
means of a statistical model in the form of a product of
MRF. The goal of those fields is to set restrictions on
the activity patterns smoothness as prior information.
The formulation of the model is made in a simple and
natural way thanks to a small number of parameters.
Besides, the Bayesian approach provides the model of
adaptability to fMRI data and makes it efficient.
The extension of this model by a single spatiotem-
poral Bayesian model allows us to obtain more in-
formation regarding the corresponding magnetic reso-
nance study. In spite of the higher computational cost,
a spatiotemporal model improves the inference ability
since it takes into account the uncertainty in both the
spatial and the temporal dimension.
3.1 The Hemodynamic Response
Function
The archetypical HRF (see figure 1) describes the lo-
cal response to the oxygen utilisation (by nerve cells)
BRAIN ACTIVITY DETECTION - Statistical Analysis of fMRI Data
435

Figure 1: Archetypical hemodynamic response curve.
and it consists of an increase in blood flow to re-
gions of increased neural activity, occurring after a
delay of approximately 1-5 seconds. This hemody-
namic response rises to a peak over 4-8 seconds, be-
fore falling back to the baseline (and typically under-
shooting slightly). This leads to local changes in the
relative concentration of oxyhaemoglobin and deoxy-
haemoglobin and changes in local cerebral blood vol-
ume in addition to this change in local cerebral blood
flow. This delayed response is characterized by h(τ),
where τ is the time since activity started.
Here we adopt the Poisson curve proposal (Friston
et al., 1994) and we model the HRF, for each pixel s,
by a scaled and shifted Poisson distribution density
function with mean d
s
, that is, a potential increase of
signal and a subsequent exponential decay,
h
s
(τ) =
(
x
s
d
τ−1
s
e
−d
s
(τ−1)!
τ = 1, 2, . .. , T − 1
0 τ = 0
where x
s
∈ [0, ∞] and d
s
∈ [0, T − 1]. Consequently,
parameter d can be interpreted as the delay of the re-
sponse with respect to the stimulus onset and x as a
measure of the magnitude of response.
3.2 Model Description
We consider a 2-dimensional block-design fMRI
study. Two consecutive blocks (a stimulation and a
resting block) are called a cycle, i.e., each cycle is
composed by T images, half of which are taken when
the stimulus is on and half when the stimulus is off.
Let y = {y
s,τ
: s = 1, . .. , N × M;τ = 0, . . . , T − 1}
be the mean of the observed hemodynamic response
curves to the stimulus paradigm. The set y plays the
role of data in our model (we take the mean to allevi-
ate the computational burden).
As the spatiotemporal model, we propose the fol-
lowing expression:
y
s,τ
= z
s
x
s
d
τ−1
s
e
−d
s
(τ − 1)!
+ ε
s,τ
+ k
s
+ ε
0
s,τ
where k is the set of basal values for each pixel that
we estimate from the mean of the first images in the
experiment (acquired when the stimulus is off).
We consider z = {z
s
: s = 1, . . . , N ×M} to be a bi-
nary random field that indicates the activity presence
or absence for each pixel of the image. To incorpo-
rate spatial connectedness (expected from activity),
we define z from thresholding of a continuous field,
w, i.e., z
s
= I
{w
s
>0}
for s = 1, . . ., N × M.
The error in the activity estimation and in the basal
values are, respectively, ε
s,τ
and ε
0
s,τ
, for which we
assume the distributions
ε
0
s,τ
∼ N (0, η
2
s,τ
),
ε
s,τ
∼ N (0, σ
2
s,τ
).
Assuming independence between variables and that
σ
2
s,τ
= σ
2
and η
2
s,τ
= η
2
, we obtain
y
s,τ
∼ N
z
s
x
s
d
τ−1
s
e
−d
s
(τ − 1)!
+ k
s
, z
s
σ
2
+ η
2
.
3.3 Prior Distributions
When image analysis problems are treated under a
Bayesian perspective, it is necessary to formulate a
prior distribution for the image of interest, in this case,
the x field and the generator field of z, w. MRF are an
adequate tool for this purpose as they define expected
characteristics of the image as, for example, smooth-
ness and connection between regions (Winkler, 2003).
Making use of MRF as prior distributions for the
image of interest, activity location in a pixel is deter-
mined by its response magnitude and also by the ac-
tivity evidence in its neighbouring pixels. That is, we
establish, a priori, the expectation that activity takes
the form of regions made up of several neighbouring
pixels, penalising activity presence in isolated pixels.
Additionally, MRF can be considered as smoothing
kernels and therefore, its use as prior distributions let
us dispense with data smoothing process during the
pre-process.
The prior distribution for w is an intrinsic Gaus-
sian Markov Random Field (Rue and Held, 2005) of
first order:
π(w) ∝ exp{−
1
2
∑
s∼t
(w
s
− w
t
)
2
}. (1)
The prior distribution for w is improper as it corre-
sponds to the bidimensional generalization of a ran-
dom walk. Combining it with the likelihood, marginal
distribution for each w
s
becomes proper. The advan-
tage of using an intrinsic form for w is that there is
no need to specify a priori the proportion of activated
pixels.
Following the proposal of (Kornak, 2000), we de-
scribe the x–field by the means of the natural log-
arithm of a proper Gaussian Markov Random Field
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
436
(Rue and Held, 2005), i.e.:
log(x) ∼ N M V (µ1, κ
2
(I − βN)
−1
), (2)
where N = (n
i j
)
i, j=1,...,N×M
and n
i j
= 1 if pixels i and
j are neighbours and n
i j
= 0, otherwise. The mean
parameter µ controls the mean level of the response
magnitude, κ
2
controls the spatial smoothness of the
response level and β models the strength of influence
that neighbouring pixel values have on each other rel-
ative to that of the field’s global mean level µ.
For µ and κ
2
we take conjugate prior distributions:
µ ∼ N (µ
1
, σ
2
1
),
κ
2
∼ GI(a
1
, b
1
),
but with large variances, to make them be almost non
informative.
In the case of β parameter a conjugate prior distri-
bution does not exist and therefore, given the flexibil-
ity of Beta distribution, we propose:
4β ∼ Be(p, q)
and hence, β ∈ [0, 0.25].
Prior distributions for the rest of parameters and
hyperparameters are:
π(d) ∼ N (µ
2
, σ
2
2
)
π(σ
2
) ∼ GI (a
2
, b
2
)
π(η
2
) ∼ GI (a
3
, b
3
)
We obtain the posterior distribution combin-
ing prior information with the likelihood under a
Bayesian approach. Given the model’s complexity, to
make inference over the parameters we use MCMC
methods (Gilks et al., 1996).
4 RESULTS
To test the model applicability and sensitivity, we use
a fMRI data simulation. We created this simulated
study from a real fMRI rest study made in the Ru-
ber Internacional hospital with a 3T machine. We
selected a central slice and we convolved it with an
activation pattern. This activation pattern takes the
shape of a gamma distribution in the temporal dimen-
sion and of different geometric figures to model spa-
tial activation regions. The result is a series of bidi-
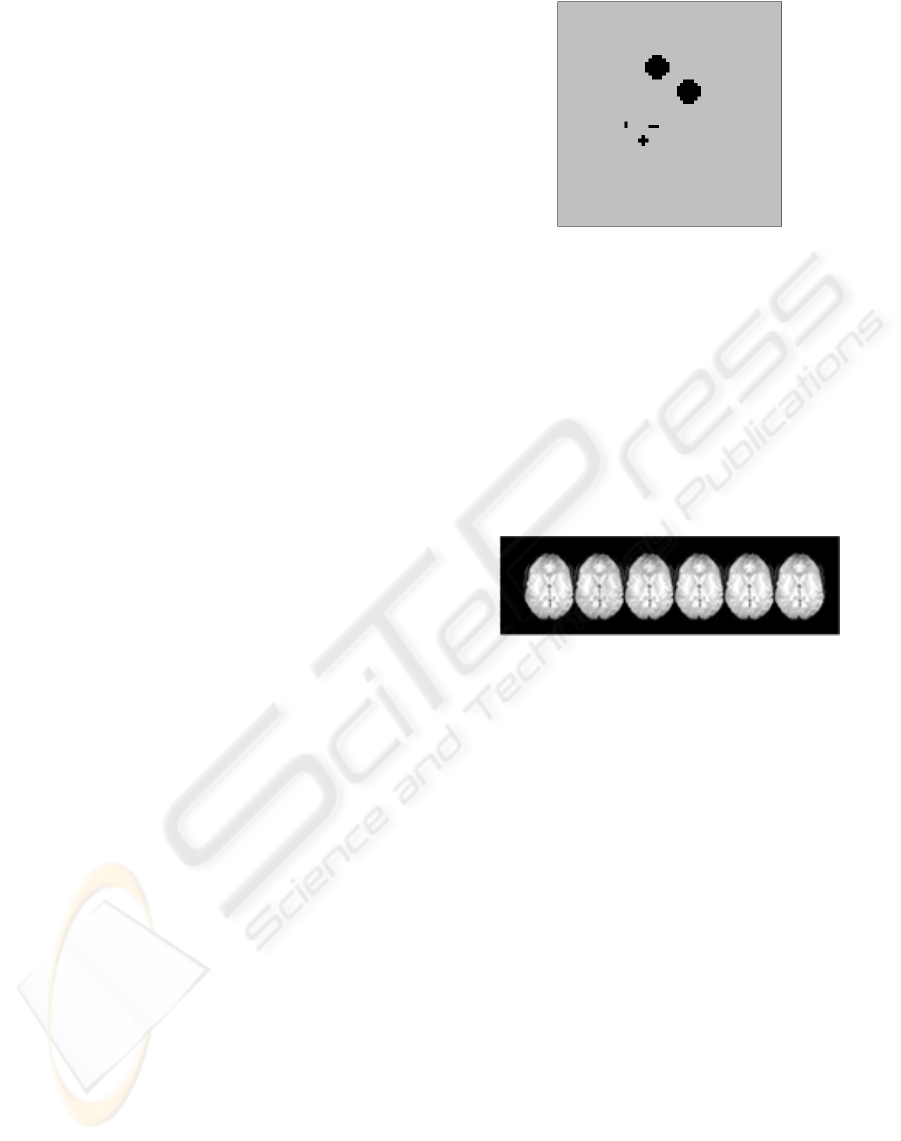
mensional slices N × M = 64 × 64 pixels. Figure 2
shows the phantom that we use to simulate the activ-
ity. Pixels of different regions have different signal
intensity (1% and 2% of the signal). The simulated
study resembles a block-design experiment with 70
scans: 3 cycles of T = 20 images each plus a rest pe-
riod at the beginning of the experiment (to calculate
Figure 2: Activity phantom used to simulate the response
paradigm to an stimulus in the simulated study.
k, the baseline value for each pixel map). In each cy-
cle, the first ten images are taken while the stimulus
is on and the last ten images when it ceases. Figure 3
shows several slices of the simulated study. Some of
them are taken during the rest period and some dur-
ing the activity period. We observe that, to the human
eye, there are no notable differences between them,
and consequently it is not possible to discriminate ac-
tivity regions at sight.
Figure 3: Several slices of the study.
Using MCMC methods, we obtained a total of
12000 samples, 4000 of which were discarded as
burn-in. Subsequently, 8000 samples were used for
posterior inference.
In the temporal dimension, we observe for each
pixel how the hemodynamic response curve is fitted
by a Poisson distribution of parameter d
s
, multiplied
by a scale factor (for the curve to reach the response
magnitude), x
s
. Figure 4 shows the fitting for one of
the active pixels. It can be appreciated that the em-
pirical curve (in black) is essentially noisy and that it
adopt the archetypical shape of the hemodynamic re-
sponse described above. In the same figure, the red
curve corresponds to the Poisson curve that fits the
empirical one.
In the spatial dimension, we obtained results in re-
lation to the activation regions’ shape together with its
magnitude. The z–field posterior mean map provides
us, for each pixel, of the posterior probability of acti-
vation.
Figure 5 shows how the model is sensitive to con-
nected activation regions, rejecting posible activation
in isolated pixels, as a neurologist might judge. This
is achieved thanks to the z–field construction from a
BRAIN ACTIVITY DETECTION - Statistical Analysis of fMRI Data
437
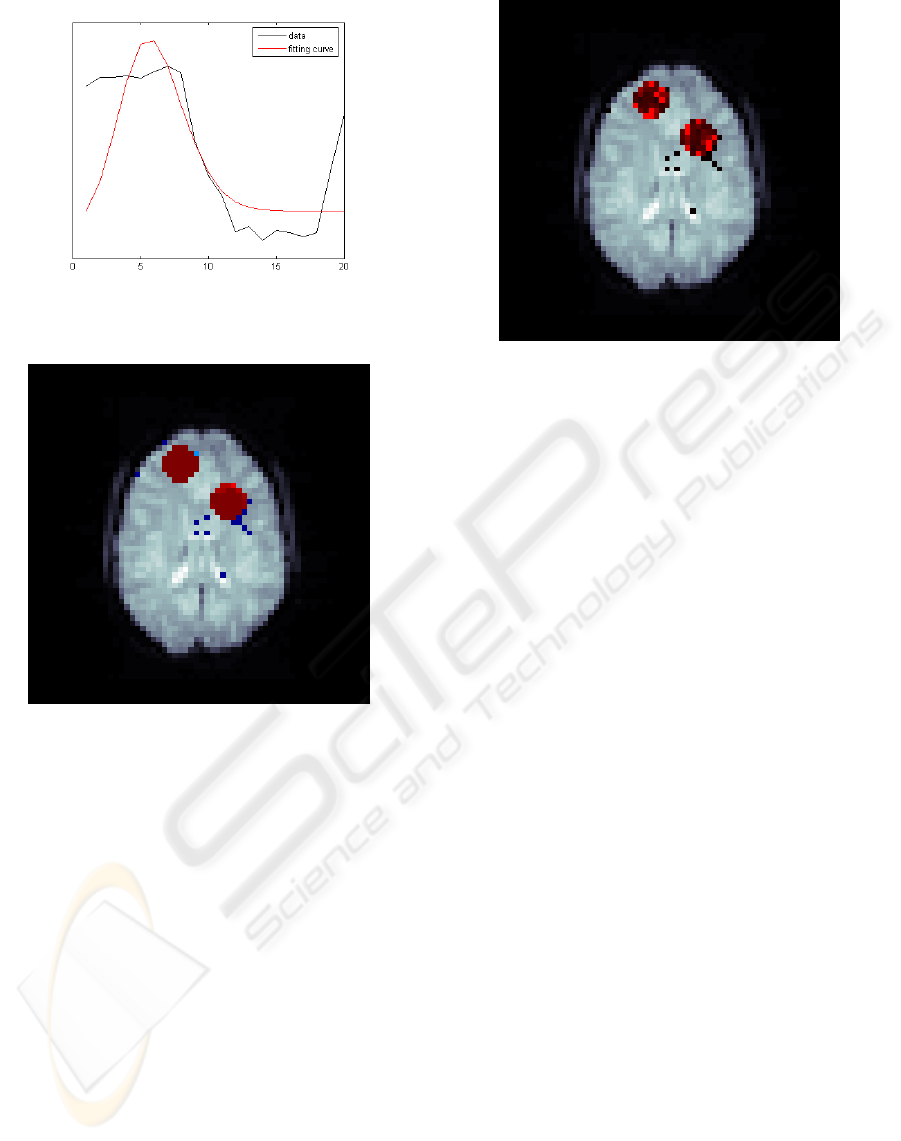
Figure 4: Hemodynamic response curve fit in an active
pixel.
Figure 5: z–field posterior mean map.
continuous field w, whose prior distribution is a MRF,
that favours this kind of regions.
Finally, figure 6 shows the result of multiplying
pixel by pixel the z and the x fields, obtaining a mag-
nitude of activation “image” in those activated areas.
5 DISCUSSION
The Bayesian model developed here incorporates spa-
tial restrictions in order to estimate response patterns
to stimulus in fMRI experiments using MRF as prior
distributions. These MRF act as two-level spatial
smoothing filters: parameter estimation in the x–field
(the classical level) and pixel activity identifying in
the z–field. This smoothing process is made taking
into account the information provided by the neigh-
bours of a pixel, apart from the pixel value itself.
In addition, including temporal information into
the spatial model (forming a spatiotemporal model),
a source of information that other models do not take
Figure 6: Active regions magnitude of activation map, xz.
into account is incorporated, without a significant in-
crease of computational cost in our model. This
would permit improvement of the model in the future,
for example, extending the model to all data (and not
only to the mean with respect to cycles), including the
baseline field, k, as another parameter (instead of es-
timating it beforehand) and integrating the model into
a graphical interface.
ACKNOWLEDGEMENTS
The authors would like to thank financial support
of the following projects TEC2006-13966-C03-01,
MTM2006-14961-C05-05 and TSI2007-66706-C04-
01 .
REFERENCES
Beckmann, C. F. and Smith, S. M. (2004). Probabilistic
independent component analysis for functional mag-
netic resonance imaging. IEEE Transactions on Med-
ical Imaging, 23(2):137–152.
Bowman, F. D. (2007). Spatiotemporal models for re-
gion of interest analysis of functional neuroimaging
data. Journal of the American Statistical Association,
102(478):442–453.
Bowman, F. D., Caffo, B. S., Bassett, S. S., and Kilts, C.
(2008). A bayesian hierarchical framework for spatial
modeling of fmri data. NeuroImage, 39(1):146–156.
Calhoun, V. D., Adali, T., McGinty, V. B., Pekar, J. J., Wat-
son, T. D., and Pearlson, G. D. (2001). fmri activation
in a visual-perception task: Network of areas detected
using the general linear model and independent com-
ponents analysis. NeuroImage, 14(5):1080–1088.
Esposito, F., Seifritz, E., Formisano, E., Morrone, R., Scara-
bino, T., Tedeschi, G., Cirillo, S., Goebel, R., and
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
438

Di Salle, F. (2003). Real-time independent com-
ponent analysis of fmri time-series. NeuroImage,
20(4):2209–2224.
Frackowiak, R. S. J., Friston, K. J., Frith, C. D., Dolan,
R. J., Price, C. J., Zeki, S., Ashburner, J. T., and Penny,
W. D. (2004). Human Brain Function. Academic
Press.
Friston, K. J. (1994). Functional and effective connectivity
in neuroimaging: A synthesis. Human Brain Map-
ping, 2:56–78.
Friston, K. J., Ashburner, J., Kiebel, S., Nichols, T., and
Penny, W. (2006). Statistical Parametric Mapping:
The Analysis of Functional Brain Images. Elsevier,
London.
Friston, K. J., Holmes, A. P., Poline, J., Gransby, P. J.,
Williams, S. C. R., Frackowiak, J., R. S., and Turner,
R. (1995). Analysis of fmri time - series revisited.
NeuroImage, 2(1):45–53.
Friston, K. J., Jezzard, P., and Turner, R. (1994). Analysis
of functional mri time-series. Human Brain Mapping,
1(2):153–171.
Gilks, W. R., Richardson, S., and Spiegelhalter, D. J.
(1996). Markov Chain Monte Carlo in Practice.
Chapman & Hall/CRC.
Gossl, C., Auer, D. P., and Fahrmeir, L. (1999). A bayesian
approach for spatial connectivity in fmri. Poster No.
483 Biometrics, 57:554–562.
Gossl, C., Auer, D. P., and Fahrmeir, L. (2001). Bayesian
spatiotemporal inference in functional magnetic reso-
nance imaging. Biometrics, 57(2):554–562.
Goutte, C., Toft, P., Rostrup, E., Nielsen, F. A., and Hansen,
L. K. (1999). On clustering fmri time series. Neu-
roImage, 9(3):298–310.
Harrison, L. M., Penny, W., Ashburner, J., Trujillo-Barreto,
N., and Friston, K. J. (2007). Diffusion-based spatial
priors for imaging. NeuroImage, 38(4):677–695.
Hartvig, N. and Jensen, J. (2000). Spatial mixture
modelling of fmri data. Human Brain Mapping,
11(4):233–248.
Holmes, A. (1995). Statistical Issues in Functional Brain
Mapping. Chapter 5 – An Empirical Bayesian Ap-
proach. PhD thesis.
Huang, H. (1999). PACS: basic principles and applications.
Wiley-Liss, New York.
Jezzard, P., Matthews, P. M., and Smith, S. M. (2001).
Functional MRI: An introduction to methods. Oxford
University Press, New York.
Katanoda, K., Matsuda, Y., and Sugishita, M. (2002). A
spatio-temporal regression model for the analysis of
functional mri data. NeuroImage, 17(3):1415–1428.
Kornak, J. (2000). Bayesian Spatial Inference from Haemo-
dynamic Response Parameters in Functional Mag-
netic Resonance Imaging. PhD thesis, University of
Nottingham.
Lange, N. and Zeger, S. L. (1997). Non - linear fourier
time series analysis for human brain mapping by func-
tional magnetic resonance imaging. Applied Statistics,
46(1):1–29.
McKeown, M. J., Hansen, L. K., , and Sejnowsk, T. J.
(2003). Independent component analysis of functional
mri: what is signal and what is noise? Current Opin-
ion in Neurobiology, 13(5):620–629.
Ogawa, S., Lee, T. M., Kay, A. R., and Tank, D. W. (1990).
Brain magnetic resonance imaging with contrast de-
pendent on blood oxygenation. Proceedings of the
National Academy of Sciences of the United States of
America, 87(24):9868–9872.
Penny, W. D., Trujilllo-Barreto, N. J., and Friston, K. J.
(2005). Bayesian fmri time series analysis with spatial
priors. NeuroImage, 24(2):350–362.
Porill, J., Stone, J. V., Mayhew, J. E. W., Berwick, J., and
Coffey, P. (1999). Spatio - temporal data analysis us-
ing weak linear models. In Mardia, K., otro, and otro,
editors, Spatial Temporal Modelling and its Applica-
tions, pages 17–20.
Quir
´
os, A., Montes, R., and Hernandez, J. (2006). A fully
bayesian two - stage model for detecting brain ac-
tivity in fmri. Lecture Notes in Computer Science,
4345:334–345.
Rue, H. and Held, L. (2005). Gaussian Markov Ran-
dom Fields: Theory and Applications, volume 104
of Monographs on Statistics and Applied Probability.
Chapman & Hall/CRC, London.
Sj
¨
ostrand, K., Lund, T. E., Madsen, K. H., and Larsen,
R. (2006). Sparse PCA, a new method for unsuper-
vised analyses of fmri data. In Proc. International So-
ciety of Magnetic Resonance In Medicine - ISMRM
2006, Seattle, Washington, USA, Berkeley, CA, USA.
ISMRM.
Winkler, G. (2003). Image Analysis, Random Fields and
Markov Chain Monte Carlo Methods. A Mathematical
Introduction. Springer, cop.
Woolrich, M. W., Behrens, T. E. J., and Smith, S. M.
(2004a). Constrained linear basis sets for hrf
modelling using variational bayes. NeuroImage,
21(4):1748–1761.
Woolrich, M. W., Jenkinson, M., Brady, J. M., and Smith,
S. M. (2004b). Fully bayesian spatio - temporal mod-
eling of fmri data. IEEE Transactions on Medical
Imaging, 23(2):213–231.
BRAIN ACTIVITY DETECTION - Statistical Analysis of fMRI Data
439
