GEOMETRY CLOSURE FOR HEMODYNAMICS SIMULATIONS

J. Bruijns

Philips Research, High Tech Campus 36, 5656 AE, Eindhoven, The Netherlands

R. Hermans

Philips Healthcare, Veenpluis 8, 5684 PC, Best, The Netherlands

Keywords:

3D rotational angiography, Computer assisted diagnosis, Hemodynamics simulations.

Abstract:

Physicians may treat an aneurysm by injecting coils through a catheter into the aneurysm, or by anchoring

a stent as a ﬂow diverter. Since such an intervention is risky, a patient is only treated when the probability

of aneurysm rupture is relatively high. Hemodynamic properties of aneurysmal blood ﬂow, extracted by

computational ﬂuid dynamics calculations, are hypothesized to be relevant for predicting this rupture. Since

hemodynamics simulations require a closed vessel section with deﬁned inﬂow and outﬂow points, and since

the user can easily overlook small side branches, we have developed an algorithm for fully-automatic geometry

closure of an open vessel section. Since X-ray based ﬂow returns an indication for the needed length to have a

developed ﬂow inside the geometry, we have also developed an algorithm to create a geometry closure around

an aneurysm based on a length criterion. After both geometry closure algorithms were tested elaborately,

practicability of the hemodynamics workstation is currently being tested.

1 INTRODUCTION

Volume representations of blood vessels acquired by

3D rotational angiography after injection with a con-

trast agent (Moret et al., 1998) have a clear distinc-

tion in gray values between tissue and vessel voxels.

Therefore, these volume representations are very suit-

able for diagnosing an aneurysm, a local widening of

a vessel caused by a weak vessel wall (see Figure 1).

Physicians may treat an aneurysm by ﬁrst mov-

ing a catheter inside the aneurysm and next injecting

coils through the catheter into the aneurysm. An al-

ternative that is becoming increasingly popular is us-

ing a stent as a ﬂow diverter. Since such an interven-

tion is risky, a patient is only treated when the prob-

ability of aneurysm rupture is relatively high. So, it

is very important to be able to estimate the probabil-

ity of aneurysm rupture (see also www.aneurist.org).

Hemodynamic properties of aneurysmal blood ﬂow

are hypothesized to be relevant for predicting this rup-

ture.

Since hemodynamics simulations (i.e. computa-

tional ﬂuid dynamics calculations using for example

ﬁnite element methods) gives highly detailed results

in space and time of wall shear stress, pressure, ﬂow

Figure 1: An aneurysm inside the white rectangle.

impact regions, vorticity and “turbulent” ﬂow, hemo-

dynamics simulations can be used to assess the risk

of an aneurysm rupture (Butty et al., 2002; Venugopal

et al., 2005; Cebral et al., 2005; Castro et al., 2005).

The points where blood is ﬂowing into the ge-

154

Bruijns J. and Hermans R. (2009).

GEOMETRY CLOSURE FOR HEMODYNAMICS SIMULATIONS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 153-161

DOI: 10.5220/0001782701530161

 SciTePress

ometry and out of the geometry can be selected by

the user or derived from X-ray based ﬂow (Waechter

et al., 2008). The user may not have selected all

points needed to close the geometry; therefore, we

have developed an algorithm for fully-automatic ge-

ometry closure of an open vessel section. The basic

hypothesis of our algorithm is that the vessel branches

on the shortest paths between the selected points are

members of the ﬂow section. Connections between

these member branches and the other vessel branches

which are not marked by the user as either an inﬂow

or an outﬂow point (i.e. unintentional open connec-

tions), are closed by a blockade (further details are

given in Section 4).

X-ray based ﬂow returns amongst other things an

indication for the needed length to have a developed

ﬂow inside the geometry. Therefore, we have devel-

oped also an algorithm to create a geometry closure

around an aneurysm based on a length criterion. First,

a blockade is created at those points of the vessel

branches for which the shortest path distance to the

aneurysm is equal to this length. In a second step, a

blockade is created at those extremities of the vessels

for which the shortest path distance to the aneurysm

is less than this length (described in Section 5).

We have used 48 clinical volume datasets with an

aneurysm to test both geometry closure algorithms

elaborately (reported in Section 7).

2 RELATED WORK

In 2006 the European funded Aneurist project was

started (www.aneurist.org). This project has the goal

to provide an integrated decision support system to as-

sess the risk of cerebral aneurysm rupture in patients

and to optimize their treatments. Hemodynamics sim-

ulations on patient speciﬁc aneurysm is a part of this.

Hemodynamics simulations is a topic of increas-

ing interest. Major advances towards clinical rele-

vance and applicability have been made by dr. J. Ce-

bral of the department of computational and data sci-

ences of George Mason University, USA, VA.

Advances in ﬂow assessment directly from the X-

ray images has been made in the work of I. Waechter

(Waechter et al., 2008).

3 PREAMBLE

Our starting point is a segmented volume with tissue

voxels, aneurysm voxels and “normal” vessel voxels

(Bruijns et al., 2007), and the set of directed graphs

(one for each component of the voxel vessel struc-

tures) with nodes (one for each vessel junction, one

for each vessel extremity and one for each aneurysm

neck; nodes at the aneurysm necks are called “neck

nodes”) and skeleton branches (one for each vessel

branch) (Bruijns, 2001). A skeleton branch consists

of a set of face connected vessel voxels, called “skele-

ton voxels”. The skeleton voxels, located close to the

center line of the vessel branch, have a unique label

per vessel branch. An example is shown in Figure 2.

Figure 2: The skeleton voxels of the graphs.

The skeleton voxels are displayed in a color ac-

cording to their label but skeleton voxels with differ-

ent labels can have the same color because of the lim-

ited number of colors used for display.

The nodes are equipped with geometry (see Fig-

ure 3). A center sphere together with the center planes

give the position, the size and the delineation of the

center region (i.e. the junction). The branch spheres

together with the branch planes give the size and the

direction of the branch regions adjacent to the center

region.

4 FULLY-AUTOMATIC

GEOMETRY CLOSURE OF AN

OPEN VESSEL SECTION

Hemodynamics simulations are only possible when

all points where blood is ﬂowing into the geometry

and out of the geometry are known. The user can

select the vessel section (called “ﬂow section” from

now on) by launching a series of probes (Bruijns et al.,

2005) on to the vessel branches (see Figure 4). The

plane of such a boundary probe separates the vessel

voxels at one side of the plane from the vessel vox-

els at the other side of the plane. If the normal of

this plane is pointing into the intended ﬂow section,

GEOMETRY CLOSURE FOR HEMODYNAMICS SIMULATIONS

155

vessel boundary

direction lines

center sphere

branch sphere

center planes

branch planes

Figure 3: The node geometry.

the vessel voxels at the positive side of the plane are

members of the ﬂow section and the vessel voxels at

the negative side not.

Figure 4: Initial boundary probes; the skeleton voxels are

green; the aneurysm part is blue.

Our program connects each boundary probe to a

skeleton voxel. The corresponding skeleton voxel is

called a “boundary skeleton voxel”. Since the closure

of a ﬂow section can be checked more easily when a

boundary skeleton voxel has exactly two face neigh-

bor skeleton voxels (will be given further detail in

Section 6), and since the ﬁrst and last skeleton voxel

of a skeleton branch has either one or more than two

face neighbor skeleton voxels, boundary probes are

connected to a skeleton voxel between the ﬁrst and

last skeleton voxel of a skeleton branch (changing the

position of the probe slightly if necessary).

Since the user can easily forget small side

branches, a possible open ﬂow section (i.e. a ﬂow

section with not all skeleton branches delimited by

a probe as shown in Figure 4) can be closed fully-

automatically by the following algorithm:

1. Mark all skeleton voxels of the shortest paths,

possibly through the aneurysm, between each pair

of boundary probes as member of the ﬂow section.

The algorithm to compute the shortest path

through the aneurysm is similar as the algorithm

to compute the path for a connection tube (Bruijns

et al., 2005).

The basic hypothesis of our algorithm is that the

skeleton voxels on the shortest paths are members

of the ﬂow section. Figure 5 is an example. The

black skeleton voxels are located on the shortest

paths and thus members of the ﬂow section, the

green skeleton voxels are not (yet) members of the

ﬂow section. Note that some of the green skeleton

voxels are located in the intended ﬂow section.

Figure 5: The skeleton voxels of the shortest paths are

black, the other skeleton voxels are green.

2. Mark the open vessel nodes type 1.

After the ﬁrst step the nodes, located on the short-

est paths, have at least one skeleton branch from

which the skeleton voxel closest to this node

is a member of the ﬂow section (such a skele-

ton branch is called a “member branch” for this

node). If such a node has also a skeleton branch

from which the skeleton voxel closest to this node

is not a member of the ﬂow section (such a skele-

ton branch is called a “non-member branch” for

this node), the ﬂow section is open along that

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

156

skeleton branch (i.e. there is no boundary probe

between a member skeleton voxel and a non-

member skeleton voxel).

In some cases, a neck node (see Section 3), not

located on the shortest paths, is connected via a

very short skeleton branch to an open vessel node

type 1 (i.e. the center spheres of the two nodes

overlap). In such a case, the aneurysm borders on

the ﬂow section. Therefore, such a neck node is

also marked as an open vessel node type 1, and

the skeleton voxels of the short skeleton branch

are marked as member of the ﬂow section. Af-

ter this procedure, one or both nodes may be no

longer an open vessel node type 1 (i.e. all its

skeleton branches are member branches), but that

is taken care of during the creation of extra bound-

ary probes further on.

3. Mark the open vessel nodes type 2.

If a neck node is a member of the ﬂow sec-

tion, there will be no boundary probe between

the intended ﬂow section and the aneurysm: the

aneurysm is member of the intended ﬂow section

(i.e. the skeleton voxels of the neck nodes are con-

ceptually face connected via the aneurysm). In

this case, boundary probes are required around the

neck nodes which are not located on the shortest

paths, to close the ﬂow section.

4. Create and launch boundary probes on the non-

member branches of the open vessel nodes type 1,

just outside the center sphere. Mark all skeleton

voxels along the non-member branches between

open vessel nodes type 1 and the corresponding

boundary probe as member of the ﬂow section.

Since the new boundary probe is placed just out-

side the center sphere of the current node, the

skeleton voxels and thus the neighbor vessel vox-

els, located in the ﬂow section, become members

of the ﬂow section.

Examples of extra boundary probes are shown in

Figure 6. Comparing Figure 5 with Figure 6 re-

veals the extra black skeleton voxels on the skele-

ton branches which are now also members of the

ﬂow section.

5. Create and launch boundary probes on the skele-

ton branches of the open vessel nodes type 2, as

close as possible to the node.

Since all skeleton branches of an open vessel

node type 2 are not members of the ﬂow section,

boundary probes has to be placed on each skele-

ton branch so that the hemodynamics simulations

cannot “escape” through the aneurysm to other

vessel parts.

Figure 6: The closed ﬂow section. The skeleton voxels

of the ﬂow section are black, the other skeleton voxels are

green.

Examples of such boundary probes are shown in

Figure 6 at the top of the aneurysm, and more

clearly in Figure 7.

Figure 7: The boundary probes at a neck, not on the shortest

paths.

Remarks:

1. The initial boundary probes are created by the

user either as inﬂow or as outﬂow probes. The ex-

tra boundary probes are created by our algorithm

as blocking probes. Afterwards, the user can mark

GEOMETRY CLOSURE FOR HEMODYNAMICS SIMULATIONS

157

the extra boundary probes as an inﬂow or an out-

ﬂow probe. After the user has ﬁnished possible

adjustments, the vessel is completely closed at

the remaining blocking probes by an extra surface

mesh.

2. In some cases two open vessel nodes type 1 are

connected by a very short non-member branch.

In this case, no extra boundary probes are cre-

ated and all skeleton voxels of such a branch are

marked as members of the ﬂow section.

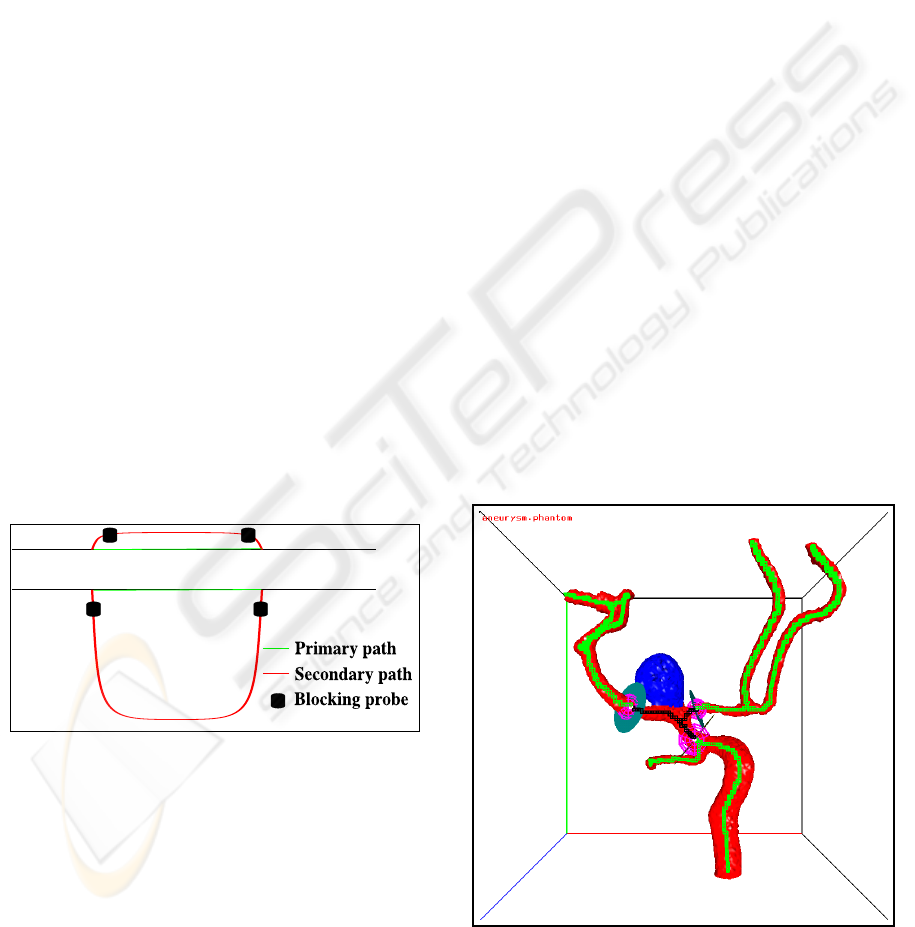
3. In some cases two open vessel nodes type 1 are

connected by two paths (i.e. there is a cycle

in the vessel graph as shown in Figure 8). Our

algorithm selects only the shortest of these two

paths (called the “primary path”). The other path

(called the “secondary path”) will be blocked by

two blocking probes at the begin and at the end

of this path. If the user wants to include also the

secondary path and if this secondary path is only

slightly longer than the primary path (top case in

Figure 8), application of our algorithm to the ex-

tended probe conﬁguration (i.e. the extra block-

ing probes become now initial boundary probes)

will include the secondary path because the short-

est path between the two blocking probes will run

along the secondary path. If the secondary path is

too long (i.e. if the shortest path between the two

blocking probes runs also along on the primary

path; bottom case of Figure 8) the secondary path

can be included by launching an extra probe on to

the secondary path.

Figure 8: Geometry closure for two cycle cases.

5 FULLY-AUTOMATIC

GEOMETRY CLOSURE OF AN

ANEURYSM

X-ray based ﬂow helps to estimate amongst other

things an indication for the needed length to have a

developed ﬂow inside the geometry (Waechter et al.,

2008). Therefore, we have developed an algorithm to

create a geometry closure around an aneurysm based

on a length criterion (i.e. a path distance in face con-

nected voxels). This algorithm consists of the follow-

ing steps:

1. Compute for each node the shortest path distance

to the aneurysm (i.e. to the closest neck node).

2. Launch a blocking probe to each skeleton branch

for which the path distance of one node is less than

or equal to the needed length and the path distance

of the other node is greater than the needed length.

Traveling along this skeleton branch, the probe is

connected to the ﬁrst skeleton voxel for which the

path distance is greater than or equal to the needed

length. Since a boundary skeleton voxel should be

located between the ﬁrst and last skeleton voxel

of a skeleton branch, the second skeleton voxel is

used when the ﬁrst skeleton voxel fulﬁlls the dis-

tance condition, and the last but one is used when

the last skeleton voxel fulﬁlls the distance condi-

tion.

3. Launch a blocking probe to each skeleton branch

for which one node is an extremity node with

a path distance less than or equal to the needed

length. The second skeleton voxel counted from

the extremity node is used as boundary skeleton

voxel.

An example of a small ﬂow section around an

aneurysm is shown in Figure 9 and of a large ﬂow

section in Figure 10.

Figure 9: A small ﬂow section around an aneurysm. The

skeleton voxels of the ﬂow section are black, the other

skeleton voxels are green.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

158

Figure 10: A large ﬂow section around an aneurysm. The

skeleton voxels of the ﬂow section are black, the other

skeleton voxels are green.

Remark:

In some cases, small side branches should be ig-

nored in the hemodynamics simulations. In that case,

this algorithm should be adapted. It may be done as

follows. Instead of pure path distances a kind of path

expenses should be used. These path expenses are the

accumulated branch expenses along the “minimum”

path. The branch expenses of small side branches

(e.g. diameter less than a user deﬁned value) are set

to a very high value. The branch expenses of the other

branches are set to the path distance of the branch.

6 VERIFICATION

6.1 Detection of an Open Flow Section

As already mentioned in Section 4, the boundary

skeleton voxels to which the boundary probes are

launched, are located between the ﬁrst and last skele-

ton voxel of a skeleton branch. So, each boundary

skeleton voxel has exactly two face neighbor skele-

ton voxels, one located at the positive side and one

located at the negative side of the probe’s plane. The

closure of the ﬂow section will be veriﬁed by looking

at the membership of these two face neighbor skele-

ton voxels. The membership of a skeleton voxel can

be computed by the following labelling algorithm:

1. Mark all skeleton voxels with the label

“FLOW IN”, indicating that they are as yet

member of the ﬂow section.

2. Mark the boundary skeleton voxels with the la-

bel “FLOW BLOCK”, indicating that labelling

should not be continued across this skeleton

voxel.

3. Mark all skeleton voxels at the extremity nodes

with the label “FLOW OUT”, indicating that they

are not member of the ﬂow section.

4. Mark all skeleton voxels, labelled with the la-

bel “FLOW IN”, face connected to a skeleton

voxel with the label “FLOW OUT”, with the label

“FLOW OUT”, indicating that they are no longer

member of the ﬂow section. This step is repeated

until no skeleton voxels are changed anymore.

As mentioned in Section 4, the skeleton voxels of

the neck nodes are conceptually face connected

via the aneurysm. Therefore, if one of the neck

nodes (i.e. its skeleton voxel) is marked with the

label “FLOW OUT”, all neck nodes are marked

with the label “FLOW OUT”.

A possible open ﬂow section is detected by com-

paring the face neighborskeleton voxels of the bound-

ary skeleton voxels. A ﬂow section is open if and only

if both face neighbor skeleton voxels have the label

“FLOW OUT”, indicating that both skeleton voxels

are not a member of the ﬂow section.

Remarks:

1. This veriﬁcation procedure is used both for check-

ing whether the geometry closure algorithm de-

scribed in Section 4 has to be executed and for

checking whether the selected geometry closure

algorithm (i.e. the one described in Section 4 or

the one described in Section 5) resulted in a closed

ﬂow section.

2. After the labelling algorithm is ﬁnished, possible

internal probes are removed (just before check-

ing whether the ﬂow section is open or closed).

An internal probe is a probe for which both face

neighbor skeleton voxels are member of the ﬂow

section. An example of a set of initial boundary

probes with one internal probe is shown in Fig-

ure 11. The closed ﬂow section is shown in Fig-

ure 12. The ﬁnal ﬂow section with the internal

probe removed is shown in Figure 13.

6.2 Detection of Multiple Flow Sections

After possible internal probes have been removed and

the geometry closure of the ﬂow section has been ver-

iﬁed, veriﬁcation of the number of components of the

ﬂow section can be performed. After all, for hemody-

namics simulations the ﬂow section should consist of

a single connected component.

GEOMETRY CLOSURE FOR HEMODYNAMICS SIMULATIONS

159

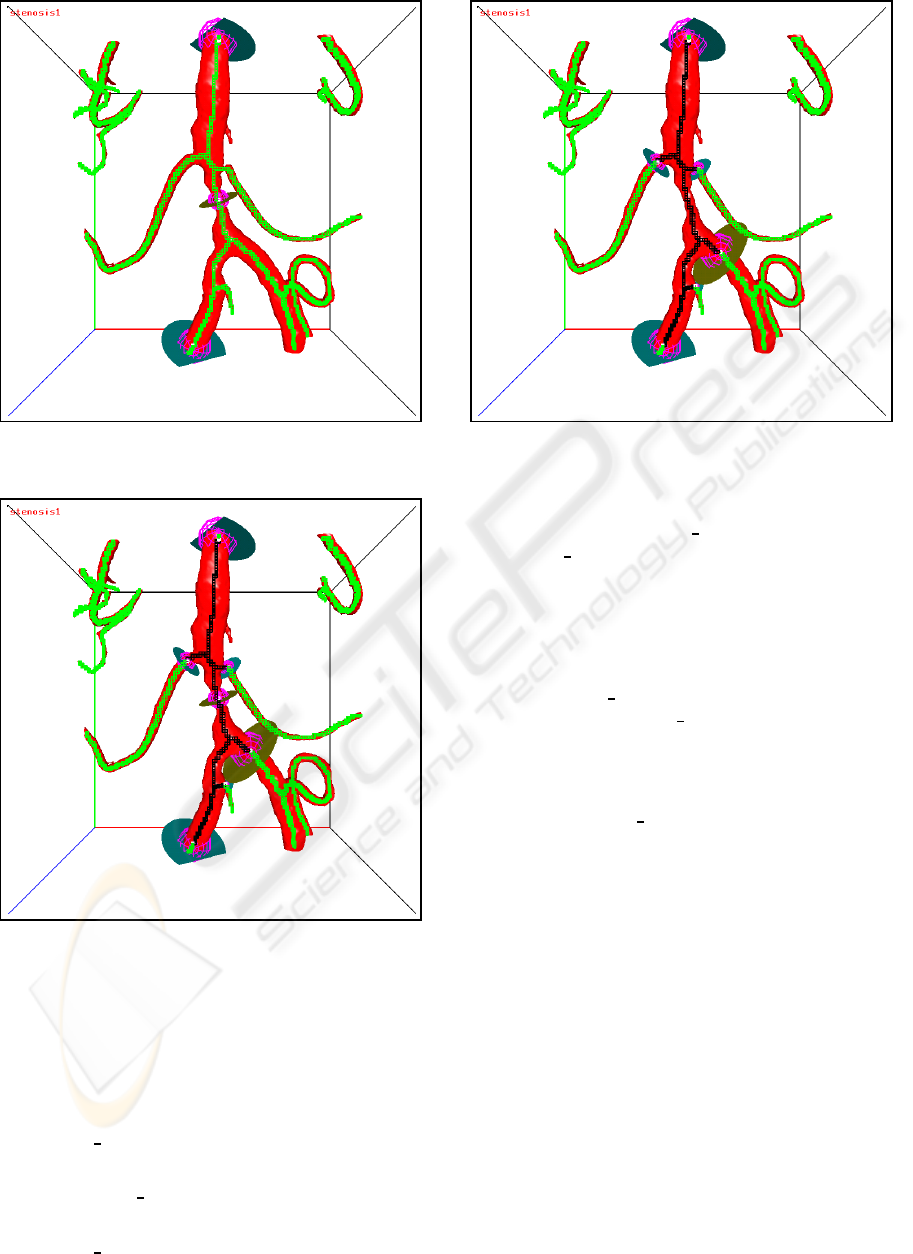
Figure 11: Initial boundary probes with one internal probe.

The skeleton voxels are green.

Figure 12: The closed ﬂow section for the internal probe

case. The skeleton voxels of the ﬂow section are black, the

other skeleton voxels are green.

Checking whether the ﬂow section consists of a

single connected component is also performed by a

labelling algorithm:

1. Mark all boundary skeleton voxels with the label

“FLOW IN”.

2. Mark the ﬁrst boundary skeleton voxel with the

label “FLOW FIRST”.

3. Mark all skeleton voxels, labelled with the label

“FLOW IN”, face connected to a skeleton voxel

Figure 13: The ﬂow section with the internal probe re-

moved. The skeleton voxels of the ﬂow section are black,

the other skeleton voxels are green.

with the label “FLOW FIRST”, with the label

“FLOW FIRST”. This step is repeated until no

skeleton voxels are changed anymore.

As mentioned in Section 4, the skeleton voxels of

the neck nodes are conceptually face connected

via the aneurysm. Therefore, if one of the neck

nodes (i.e. its skeleton voxel) is marked with the

label “FLOW FIRST”, all neck nodes are marked

with the label “FLOW FIRST”. So, two ﬂow sec-

tions connected to an aneurysm are considered a

single connected component.

4. Check whether all boundary skeleton voxels have

the label “FLOW FIRST”.

If so, the ﬂow section consist of a single connected

component.

An example of two separated closed ﬂow sections

is shown in Figure 14.

7 EXPERIMENTS AND RESULTS

7.1 For Geometry Closure of an

Aneurysm

We have applied the method for fully-automatic ge-

ometry closure of an aneurysm (see Section 5) to

48 clinical volume datasets with an aneurysm (15

of them with a resolution of 256x256x256 voxels,

the rest 128x128x128 voxels), acquired with the 3D

Integris system (Philips-Medical-Systems-Nederland,

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

160

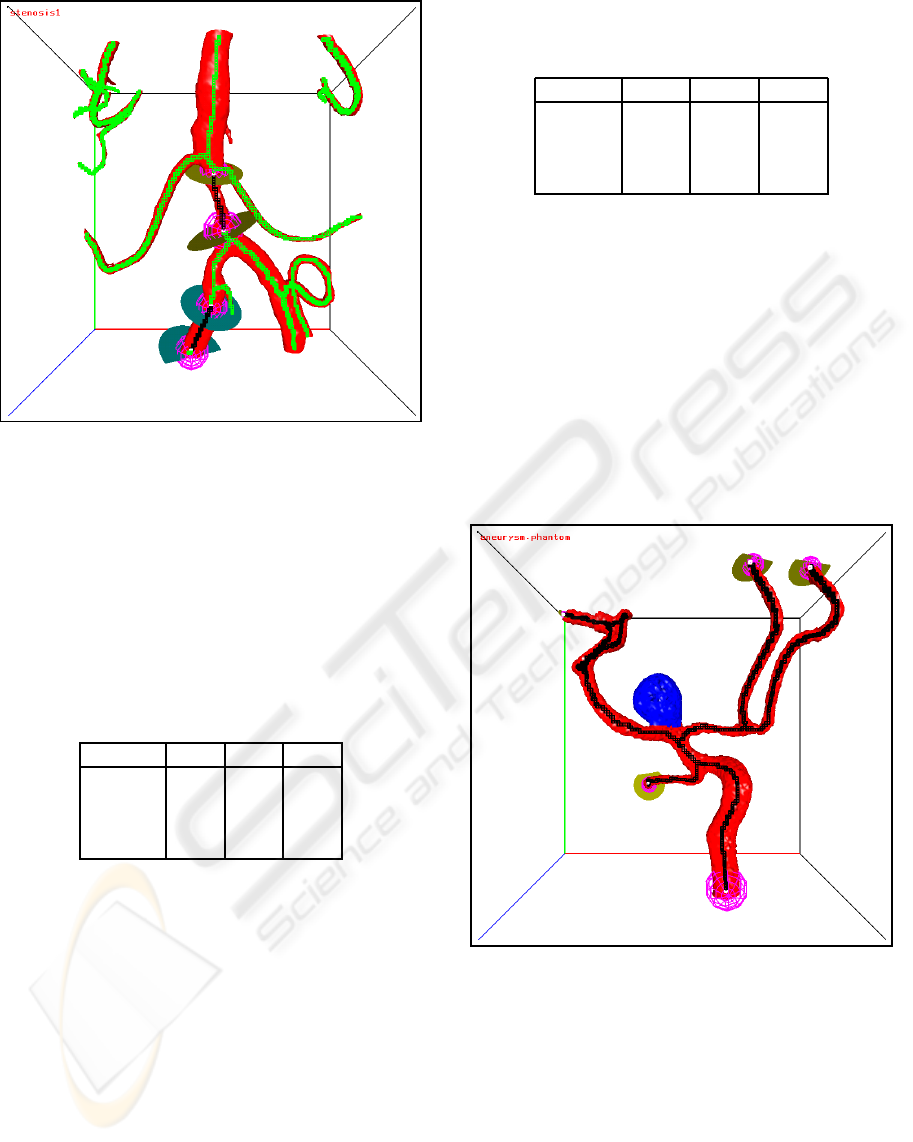
Figure 14: Two separated closed ﬂow sections. The skele-

ton voxels of the ﬂow sections are black, the other skeleton

voxels are green.

2001). The voxel size varies between 0.2 and 1.2 mil-

limeter. We have tested three lengths (path distances

in face connected voxels): 31, 101 and 171. Examples

are shown in Figure 9 and Figure 10.

Table 1: The characteristics of the number of blocking

probes, created by fully-automatic geometry closure of 48

aneurysms, for three different lengths (i.e. path distances in

face connected voxels).

Length: 31 101 171

min. 2.0 2.0 3.0

median 4.0 8.0 11.5

mean 4.3 9.1 13.7

max. 11.0 24.0 36.0

The characteristics of the number of blocking

probes, created by fully-automatic geometry closure

of 48 aneurysms, for these three lengths, are given in

Table 1. The characteristics of the elapsed times in

seconds are given in Table 2. The elapsed times for

the 256x256x256 volumes are divided by 2 to com-

pensate for the on average two times longer path dis-

tances. As is clear from this table, the elapsed times

are increasing for larger lengths.

After the blocking probes are created, the ﬂow

section is checked with the veriﬁcation algorithms,

described in Section 6. For all cases, the ﬂow section

was a single connected closed ﬂow section.

Table 2: The characteristics of the elapsed times in seconds

for fully-automatic geometry closure of 48 aneurysms, for

three different lengths.

Length: 31 101 171

min. 0.016 0.020 0.024

median 0.052 0.103 0.163

mean 0.064 0.119 0.173

max. 0.200 0.304 0.416

7.2 For Closure of an Open Flow

Section

We have applied the method for fully-automatic ge-

ometry closure of an aneurysm also to generate tests

for geometry closure of an open ﬂow section (see Sec-

tion 4). Indeed, if the required length is set to a very

large number, blocking probes will be generated at the

extremity nodes of the vessel graph(s) connected to

the aneurysm. An example of the generated extremity

probes is shown in Figure 15.

Figure 15: The extremity probes.

We have used each pair of the generated extrem-

ity probes as initial boundary probes. An example of

the generated blocking probes for two of the initial

boundary probes is shown in Figure 16.

The characteristics of the number of extremity

probes NE, the number of tests NT (i.e. the number

of pairs of initial boundary probes) and the resulting

number of blocking probes NB including the two ini-

tial probes are given in Table 3. The total number of

test was 11869. For all tests, the ﬂow section was a

single connected closed ﬂow section.

GEOMETRY CLOSURE FOR HEMODYNAMICS SIMULATIONS

161

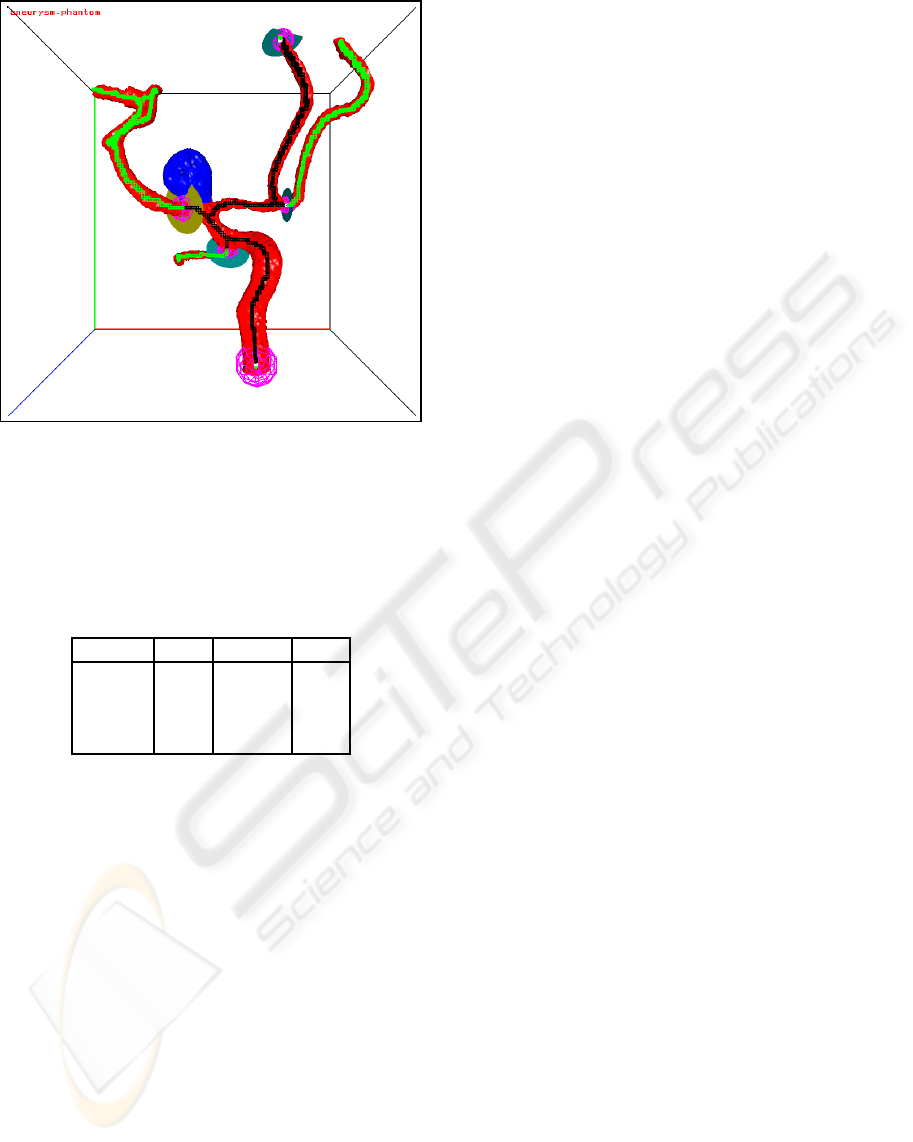
Figure 16: The closed ﬂow section for probes 1 and 3.

The skeleton voxels of the ﬂow section are black, the other

skeleton voxels are green.

Table 3: The characteristics of the number of extremity

probes NE, the number of tests NT and the resulting num-

ber of blocking probes NB including the two initial probes

for fully-automatic geometry closure of 11869 open ﬂow

sections

NE NT NB

min. 3.0 3.0 3.0

median 15.5 112.5 14.0

mean 19.2 247.3 14.8

max. 56.0 1540.0 48.0

8 CONCLUSIONS

The following conclusions can be drawn from the re-

sults, the ﬁgures and the experiences gathered during

testing:

1. Fully-automatic geometry closure of an aneurysm

gives always correct (i.e. a single connected

closed ﬂow section) and visually acceptable re-

sults.

2. Fully-automatic geometry closure of an open ﬂow

section gives correct and visually acceptable re-

sults except when multiple closed ﬂow sections

arise from the initial boundary probes.

3. Preparing patient speciﬁc geometries for compu-

tational ﬂuid dynamics is a time-consuming and

error-prone task. The work above is the ﬁrst to au-

tomatically create and validate an error free closed

simulation domain. It has been implemented in

a simulation and visualization software environ-

ment that allows a user to prepare a simulation in

a matter of minutes instead of an hour of work.

4. Whether ﬂow sections, generated by fully-

automatic geometry closure of an aneurysm based

on a length criterion, are suitable for hemodynam-

ics simulations has yet to be investigated.

REFERENCES

Bruijns, J. (2001). Fully-automatic branch labelling of

voxel vessel structures. In Proc. VMV, pages 341–350,

Stuttgart, Germany.

Bruijns, J., Peters, F., Berretty, R., and Barenbrug, B.

(2007). Fully-automatic correction of the erroneous

border areas of an aneurysm. In Proc. BVM, pages

293–297, Muenchen, Germany.

Bruijns, J., Peters, F., Berretty, R., van Overveld, C., and ter

Haar Romeny, B. (2005). Computer-aided treatment

planning of an aneurysm: The connection tube and the

neck outline. In Proc. VMV, pages 265–272, Erlangen,

Germany.

Butty, V., Gudjonsson, K., P.Buchel, Makhijani, V., Ven-

tikosa, Y., and D.Poulikakos (2002). Residence times

and basins of attraction for a realistic right inter-

nal carotid artery with two aneurysms. Biorheology,

39:387–393.

Castro, M., Putman, C., and Cebral, J. (2005). Computa-

tional modeling of cerebral aneurysms in arterial net-

works reconstructed from multiple 3d rotational an-

giography images. In Proc. SPIE: Medical Imaging,

volume 5746, pages 233–244, San Diego, CA, USA.

Cebral, J., Castro, M., Millan, D., Frangi, A., and Putman,

C. (2005). Pilot clinical investigation of aneurysm

rupture using image-based computational ﬂuid dy-

namics models. In Proc. SPIE: Medical Imaging, vol-

ume 5746, pages 245–256, San Diego, CA, USA.

Moret, J., Kemkers, R., de Beek, J. O., Koppe, R., Klotz,

E., and Grass, M. (1998). 3D rotational angiography:

Clinical value in endovascular treatment. Medica-

mundi, 42(3):8–14.

Philips-Medical-Systems-Nederland (2001). INTEGRIS

3D-RA. instructions for use. release 2.2. Techni-

cal Report 9896 001 32943, Philips Medical Systems

Nederland, Best, The Netherlands.

Venugopal, P., Duckwiler, G., Valentino, D., Chen, H.,

Villablance, P., Vinuela, F., Kemkers, R., and Haas,

H. (2005). Correlating aneurysm growth to hemody-

namic parameters: the case of a patient-speciﬁc ante-

rior communicating artery aneurysm. In Proc. SPIE:

Medical Imaging, volume 5746, pages 780–791, San

Diego, CA, USA.

Waechter, I., Bredno, J., Hermans, R., Weese, J., Barratt, D.,

and Hawkes, D. (2008). Evaluation of model-based

blood ﬂow quantiﬁcation from rotational angiography.

In Proc. SPIE: Medical Imaging, volume 6916, San

Diego, CA, USA.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

162