A TOP DOWN CONSTRUCTION SCHEME FOR IRREGULAR

PYRAMIDS

Romain Goffe

SIC-XLIM, Universit

e de Poitiers, CNRS, UMR6172, B

atiment SP2MI, F-86962, Futuroscope Chasseneuil, France

Luc Brun

GREYC, ENSICAEN, CNRS, UMR6072, 6 Boulevard du Mar

echal Juin, F-14050, Caen, France

Guillaume Damiand

LIRIS, Universit

e Lyon, CNRS, UMR5205, Universit

e Lyon 1, F-69622, Villeurbanne, France

Keywords:

Segmentation, Irregular pyramid, Topological model, Combinatorial map.

Abstract:

Hierarchical data structures such as irregular pyramids are used by many applications related to image pro-

cessing and segmentation. The construction scheme of such pyramids is bottom-up. Such a scheme forbids the

deﬁnition of a level according to more global information deﬁned at upper levels in the hierarchy. Moreover,

the base of the pyramid has to encode any single pixel of the initial image in order to allow the deﬁnition of

regions of any shape at higher levels. This last constraint raises major issues of memory usage and processing

costs when irregular pyramids are applied to large images. The objective of this paper is to deﬁne a top-down

construction scheme for irregular pyramids. Each level of such a pyramid is encoded by a combinatorial map

associated to an explicit encoding of the geometry and the inclusion relationships of the corresponding parti-

tion. The resulting structure is a stack of ﬁner and ﬁner partitions obtained by successive splitting operations

and is called a top-down pyramid.

1 INTRODUCTION

Quadtrees (Dyer et al., 1980; Jolion and Rosenfeld,

1994) and regular pyramids (Jolion and Rosenfeld,

1994) belong to the ﬁrst hierarchical data structures

introduced within the computer vision framework.

Both models are based on psycho-visual properties:

focus of attention, for data structure based on recur-

sive split such as quadtrees, and successive process-

ings by neural layers, for bottom-up regular pyramids.

Segmentation using quadtree data structures is based

on a recursive subdivision of a basic shape (e.g. a

square). On the other hand, regular or matrix pyra-

mids are deﬁned as a stack of images with decreasing

resolutions. An entity (square or pixel) deﬁned at a

given level of a pyramid is associated to a connected

set of entities below, called a reduction window (Bis-

ter et al., 1990). Both encoding schemes induce sev-

eral drawbacks on the segmentation process (Bister

et al., 1990).

The irregular pyramid framework introduced by

Meer and Montanvert (Meer, 1989; Montanvert et al.,

1991) partially solves these drawbacks: the stack of

partitions is encoded as a stack of successively re-

duced graphs. Irregular pyramids (Meer, 1989; Mon-

tanvert et al., 1991; Jolion and Montanvert, 1992;

Brun and Kropatsch, 2003) may only be built using a

bottom-up construction scheme. However, a bottom-

up scheme requires an explicit encoding of the base

level image in order to deﬁne regions with any shapes

at higher levels. Moreover, in a bottom-up pyramid,

each newly created region has no prior information

about its parents (deﬁned at a later stage). This last

constraint prevents the management of the regions

from depending on the properties of their parents in

the pyramid.

The objective of this paper is the deﬁnition of

a top-down hierarchical data structure by extending

the model of two-dimensional topological maps. For

many applications related to image segmentation, it is

163

Goffe R., Brun L. and Damiand G. (2009).

A TOP DOWN CONSTRUCTION SCHEME FOR IRREGULAR PYRAMIDS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 162-169

DOI: 10.5220/0001782901620169

 SciTePress

critical to minimize memory requirements, mainly for

those processing large images. A top-down approach

rules out the constraint of the explicit storage for the

base: only split regions are kept in memory. Besides,

it offers a perceptual advantage as major features of

an image are discerned ﬁrst in the pyramid, contrary

to bottom-up models.

We ﬁrst recall in Section 2, the basics of the dif-

ferent models used to deﬁne our top-down irregu-

lar pyramid framework. Then, Section 3 deﬁnes our

model of top-down pyramid. We present in Section 4

its construction scheme. Section 5 details the basic

operations used to build a new level of the pyramid.

We ﬁnally provide, in Section 6, several experiments

which allow to evaluate the computational times and

memory requirements of our model.

2 RECALLS

2.1 Combinatorial Maps

A combinatorial map encodes all the subdivisions and

incidence relationships of a topological space (Lien-

hardt, 1989). In two dimensions, it is composed of

vertices, edges and faces, respectively deﬁned as cells

of 0, 1 and 2 dimensions and noted i-cells. The bor-

der of an i-cell is a set of ( j < i)-cells. Two i-cells are

said incident if one belongs to the border of the sec-

ond while they are said adjacent if they are both inci-

dent to the same ( j < i)-cell. The degree of an i-cell

is the number of adjacent (i + 1)-cells and a dangling

edge is an edge incident to a degree 1 vertex. Adja-

cency relations are represented by operators noted β

and applied to darts, as we will call the abstract basic

elements resulting from a complete decomposition of

the image (Figure 1).

Deﬁnition 1 (2-dimensional Combinatorial Map).

A two-dimensional combinatorial map M (or 2-map)

is a triplet M = (D, β

, β

) where:

(1) D is a ﬁnite set of darts;

(2) β

is a permutation

on D;

(3) β

is an involution

on D.

Intuitively, a combinatorial map may be under-

stood as a planar graph where relations on edges are

explicitly deﬁned by β

operators. Darts allow to dif-

ferentiate the two extremities of an edge and thus, are

A permutation is a one to one mapping from S onto S.

An involution f is a one to one mapping from S onto S

such that f = f

−1

Figure 1: Construction of a 2-map by successive decom-

positions. (A) Original image. (B) Disconnected faces.

ements represented by arrows, β

relations are represented

with arcs and β

with bold segments.

assimilated to half-edges. Each dart belongs to a sin-

gle vertex, edge and face of the map. The β

permuta-

tion links each dart of a face to the next dart encoun-

tered while turning clockwise around the face (Fig-

ure 1). The β

involution links each dart of an edge

to the other dart of the edge which has an opposite

orientation (shared edge between the square and the

triangle in Figure 1). Two darts linked by β

are said

i-sewn and two 2-sewn darts belong to two adjacent

faces.

2.2 Topological Maps

Because 2-maps can only represent the topology of

connected objects, we introduce the notion of topo-

logical maps (Brun et al., 2003; Damiand et al., 2004),

an extension of combinatorial maps that uses three

different models to encode: topological relations, ge-

ometrical information and inclusion relationships be-

tween regions.

Topology is based on a 2-map which is minimal

according to its number of cells (Figure 3.A). Al-

though combinatorial maps only represent the topol-

ogy of the space, geometric elements can be added

easily. This association is called embedding. The

geometry relies on the interpixel framework where

an image is considered as a subdivision of a two-

dimensional space in a set of 2-cells, 1-cells and 0-

cells, respectively called pixels, linels, and pointels

(Figure 2). Each border between two regions is thus

deﬁned as a set of linels. Since each dart corresponds

to an oriented boundary, the embedding of a dart de-

ﬁnes an order over the set of linels belonging to this

border. The set of linels composing a dart can be rep-

resented explicitly as a sequence of linels or implic-

itly, using a two-dimensional matrix of the size of the

image (Brun et al., 2003; Damiand et al., 2004) (Fig-

ure 3.B).

A region is a set of darts delimited by a β

-loop.

Each one has a representative dart which allows to re-

trieve a dart of a given region (e.g. used as a starting

point to ﬁnd the external border of the region). A set

of adjacent regions is called a connected component

and the union of all the regions create a topologically

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

164

Figure 2: Representation of the interpixel framework: an

image is composed of pixels, linels and pointels.

closed space since we represent the inﬁnite region

which encodes the background of the image. A region

included into another one is called a hole and deﬁnes

an internal border for the including region. An inclu-

sion tree of regions represents the inclusion relation-

ships of the structure: the father of any region within

the tree is deﬁned as the one which includes it in the

image (Figure 3.C).

Figure 3: The three different models composing a topologi-

cal map. (A) A 2-map representing the topology with darts

and β

relations. (B) A geometrical matrix that points out

active linels and pointels. (C) A tree of regions for inclu-

sion relations.

A topological map is a suitable model for image

processing which has been proven complete (repre-

sents both topology and geometry), minimal (retiring

any element would change the topology) and unique

(two topologically equivalent partitions have the same

map) (Damiand et al., 2004). In practice, the min-

imality is required to decrease the number of cells

and minimize memory usage and the completeness

insures that we can encode partitions with regions of

any geometry.

2.3 Pyramids

Simple graph pyramids, ﬁrst introduced by Meer and

Montanvert (Meer, 1989; Montanvert et al., 1991),

then developed by Jolion (Jolion and Montanvert,

1992) are deﬁned as a stack of simple graphs succes-

sively reduced. Within the segmentation framework,

each graph of such a pyramid encodes a partition. Due

to the limitation of the simple graph data structure,

many issues are encountered when we have to update

these graphs after splitting operations.

For visibility reasons, the inﬁnite region may not be

represented in some ﬁgures.

Combinatorial pyramids (Brun and Kropatsch,

2003) are built from an initial combinatorial map suc-

cessively reduced by a sequence of contractions and

removal operations. These operations are ruled by

a contraction kernel (forest of the initial combinato-

rial map) and a removal kernel (forest of the dual

combinatorial map). These structures are bottom-up

and the initial combinatorial map (the base) is the

most detailed level: the embedding of each dart of

the base corresponds to a linel. Therefore, the recep-

tive ﬁeld of any dart may be retrieved from its recep-

tive ﬁeld and the embedding of the darts deﬁned at

the base (Brun and Kropatsch, 2003). Besides, using

forests avoids disjunctions of connected components

when performing merging operations: two connected

components are linked by a bridge if one is included

into the other (Brun and Kropatsch, 2006). The model

of bottom-up combinatorial pyramid has been gen-

eralized to encode all n-dimensional, orientable or

not and with or without boundary subdivisions (Lien-

hardt, 1989; Simon et al., 2006).

Contrary to bottom-up methods, based on an ex-

plicit encoding of the base of the pyramid, a top-down

approach allows to encode only the upper levels, re-

sulting in a major memory reduction. Moreover, the

focus of attention, encoded by the top-down scheme,

can adapt the segmentation of each region according

to the features of its parents (e.g. with medical im-

ages, the segmentation of cells in a tissue depends on

the tissue itself). Within a top-down scheme, we have

to give up on bridges to represent inclusion relation-

ships. Indeed, the management of the additional con-

nections encoded by the bridges during splitting op-

erations may induce cumbersome computations. For

example, the insertion of an edge at the two endpoints

of a bridge may create an artiﬁcial face which has to

be detected and removed. This is why bridges are re-

placed by the use of inclusion tree of regions. More-

over, since the top-down construction scheme avoids

an explicit encoding of the base, the geometry of the

pyramid’s partitions cannot be implicitely encoded at

the base level. The borders of the partition have thus

to be explicitely encoded. These last arguments jus-

tify the use of topological maps as the basis of our

top-down model.

3 MODEL FOR TOP-DOWN

PYRAMIDS

Each level of our top-down pyramid model is encoded

by a topological map, deﬁned by: a 2-map for the

topology, an encoding for the geometrical embedding

of darts and a tree of regions for inclusion relation-

A TOP DOWN CONSTRUCTION SCHEME FOR IRREGULAR PYRAMIDS

165

ships.

Deﬁnition 2 (Top-down Topological Pyramid).

Let (n, m, k) ∈ N

. A top-down pyramid P is deﬁned

by P = {G

} where, ∀k, 0 ≤ k ≤ m:

(1) G

= (D

, β

) is a topological map;

(2) G

k+1

is deduced from G

by performing splitting

operations.

Since any level of the top-down pyramid results

from splitting operations (2), every region of G

has

a descendant in G

k+1

and every region of G

has at

most one antecedent in G

k−1

(same for darts). Thus,

the model is a causal structure (Guigues et al., 2006)

and deﬁnes a hierarchy of regions.

Figure 4: A top-down topological pyramid P, composed of

two levels G

and G

. Numbers designate darts, β

relations

are represented by arcs and β

by segments. G

is deduced

from G

by splitting region R

into two regions R

and R

As a hierarchical data structure, the model has to

represent objects and relations through the levels of

the pyramid. So, each dart and region of a map G

connected to its parent in G

k−1

and its child in G

k+1

(also called ascendant/descendant or up/down). Note

that, although each element (dart or region) has a sin-

gle descendant, there is no loss of information: we

can retrieve for each element the corresponding set of

elements in a lower level. Indeed, the set of children

of a given element is connected so, up and down rela-

tions allow to start from a descendant and to ﬁnd all

the neighbors which have the same “up”. Neither el-

ements from the top level nor elements newly created

on a level have an antecedent and elements belong-

ing to the base do not have a descendant but several

elements may have the same parent (Table 1).

Table 1: Parent/child relations in pyramid P from Figure 4.

(A) Between darts. (B) Between regions.

D d

down

1 - 4

2 - 5

3 1 -

4 1 -

5 2 -

6 - -

7 - -

8 2 -

R R

down

1 - 2

2 1 -

3 1 -

A B

In the following, P denotes a top-down pyramid

composed of m + 1 levels numbered from 0 to m (m

is called the depth of the pyramid). Globally, an ex-

ponent k refers to level k + 1 of the pyramid: G

the map of level k + 1, D

(resp. R

) is the set of all

darts (resp. regions) composing level k + 1. An edge

may be noted (d, d

) where d and d

are the 2-sewn

darts which compose it and R

(d) denotes the region

of dart d in level k + 1.

4 CONSTRUCTION SCHEME

This section outlines the global operations construct-

ing a pyramid. The construction is incremental: it

starts from the top and adds new levels one by one at

the bottom. It is composed of three main steps: the

construction of the ﬁrst (top) level, the creation of a

new level by copying the bottom and the segmenta-

tion of the level that has just been added.

Several methods can be considered to build the

ﬁrst level of a pyramid but only two are considered

so far. The ﬁrst method creates a map composed of a

single region enclosing the image and the inﬁnite re-

gion for the outside of the image. The second method

extracts a ﬁrst topological map from a segmentation

of the image in few regions.

We create a new level by duplicating the last one

of the pyramid. This is why, we build a map equiva-

lent to the bottom (same topology, same geometry and

same tree of regions), link corresponding elements

between the two levels, and ﬁnally, add this map at the

bottom of the pyramid (Algorithm 1 and Figure 5.B).

Algorithm 1: Duplication of a level.

Data: A pyramid P of depth m + 1.

Result: A pyramid P of depth m + 2.

Create a new void map G

m+1

;

Copy the geometry of G

into G

m+1

;

foreach dart d

∈ G

Create a new dart d

down

in G

m+1

;

Set d

as parent of d

down

;

Sew (in G

m+1

) d

down

with the

corresponding down darts of β

) and

);

foreach region R

∈ G

Create a new region R

down

in G

m+1

;

Set R

as parent of R

down

;

Establish inclusions in G

m+1

by setting the

relations of R

down

like those of R

;

Set G

as parent of G

m+1

;

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

166

The last step of the construction process is the seg-

mentation of the level that has just been duplicated.

This segmentation is based on splitting and merging

operations that transform the level (Algorithm 2).

Algorithm 2: Segmentation of a level.

Data: A level G

of a pyramid P.

Result: P with a new segmentation on level G

foreach region R ∈ G

if splitting criterion(R) is true then1

Split(R);2

Merge(G

, merging criterion);3

Simplify G

Compute the new tree of regions;5

Algorithm 2 is composed of four main steps:

• L.1: The splitting criterion indicates if a region

has to be segmented. It is used upstream from the

construction process as an optimization since it

moves uninteresting areas further apart (notion of

focus of attention (Jolion and Rosenfeld, 1994));

• L.2: This step decomposes region R into a set

of square-unit regions, each one enclosing a sin-

gle pixel (Figure 5.C). This operation is detailed

in Section 5.1;

• L.3: The merging criterion determines if two ad-

jacent regions should be merged. In order to pre-

serve the causality property, we restrict the merg-

ing operation to new regions resulting from the

split of a same region (Figure 5.D). Therefore,

two different regions of a level G

will never be

merged in a level G

, p < q. This operation is

detailed in Section 5.2;

• L.4: The simpliﬁcation step removes all remain-

ing 2-degree vertices;

• L.5: Because new regions are created, the tree for

inclusion relations has to be rebuilt. Indeed, it

would be too expensive to keep it up-to-date as

many regions are created from a level to another.

Steps L.4 and L.5 rely on the algorithms deﬁned

for topological maps (Damiand et al., 2004). Figure 5

illustrates a simple example of the building process.

5 BASIC OPERATIONS

5.1 Splitting Operation

As mentioned in Section 4, our splitting step decom-

poses a region into a set of basic regions, each one

Figure 5: Main steps of the construction process of a top-

down pyramid. (A) Initial step: the pyramid is composed

of a single level G

. (B) Duplicate and link: G

is a copy

of G

and corresponding elements are linked together (for

visibility reasons, dotted lines represent only up/down rela-

tions between regions). (C) Split: R

is split into a set of

square-unit regions enclosing a single pixel. (D) Merge and

simplify: some of the created regions are merged and draw

and R

enclosing a single pixel. Later, a merging step will

merge these regions: since any couple of adjacent re-

gions may be merged, any subdivision of the initial re-

gion can be encoded. The operation insures that each

created region is both topologically and geometrically

correct (Figure 6).

Figure 6: Decomposition in 4 steps of the splitting process

applied on a region R

enclosing 4 pixels. (A) Initial region.

(B) Splitting edges: darts 1 to 8 are stored into list (external

border of R

). (C) Insertion of 4 dangling edges while test-

ing darts 1, 3, 5 and 7. (D) Sewing correctly dangling edges

while testing darts 9 and 13.

Assuming that the region to split is denoted R, Al-

gorithm 3 describes the splitting operation which may

be divided into the following steps:

A TOP DOWN CONSTRUCTION SCHEME FOR IRREGULAR PYRAMIDS

167

Algorithm 3: Splitting region

Data: A region R.

Result: R is split into a set of basic regions

enclosing a single pixel.

Split edges of R into unit edges;1

Create list containing every dart of R;2

while ∃ d ∈ list|d is unmarked do

l ← getLinel(d);3

if l

⊥

is not activated then4

Insert edge(d

, d

) on d;5

Add(d

, d

) at the end of list;

else if β

(d) = β

(d) then

1-sew correctly d and β

(d) around the6

pointel p incident to β

(d);

Mark(d);

• L.1: All the edges belonging to the borders of R

are split into one-linel long edges to allow further

edge insertions;

• L.2: We create a list which initially contains all

the darts resulting from the previous decomposi-

tion of external and internal borders of the region;

• L.3: We retrieve the geometry associated to the

dart. As all edges have been split, the embedding

of each dart of list is a single linel;

• L.4: The external border of a region is clockwise

oriented. Let us denote by l

and l

⊥

, the oriented

linels encoding respectively the embedding of the

dart d and the next linel encountered after l

when

turning counter-clockwise around the pointel as-

sociated to d (e.g. in Figure 6, l

⊥

= l

). Since

the β

permutation connects two consecutive darts

in a clockwise orientation around a face, only l

⊥

needs to be considered at this stage. If other darts

remain around the vertex incident to β

(d), they

will be considered during further iterations.

• L.5: Actually, an edge insertion on a dart d con-

sists in adding two one-linel long darts d

and d

(whose embedding is perpendicular to l

) on the

pointel p incident to d. Two conﬁgurations may

happen as described in Figure 7;

• L.6: In order to sew the 2 darts of the dangling

edge e = (d, β

(d)), we geometrically look for

edges perpendicular to e as illustrated in Figure 8.

This operation 1-sew the two darts according to its

number (one or two) of perpendicular edges. At

least one perpendicular edge exists (inserted dur-

ing the previous iteration when processing β

(d)).

If four edges are incident to p, processing e will

sew two edges around p and the two others will

be sewn in a further iteration (Figure 6).

Figure 7: Insertion of a dangling edge on dart 1. (A) In-

sertion of edge (5, 6) on a degree 2 vertex. (B) Insertion of

edge (3, 4) on a degree 1 vertex.

Figure 8: 1-sewing operations when processing dangling

edge (1, 2). (A) One perpendicular edge: 1-sew (1, 4) and

(3, 2). (B) Two perpendicular edges: 1-sew (1, 4) and (5, 2).

This process ensures that each linel within the ini-

tial region is added. Moreover, no dangling edges re-

main: the initial region is initially minimal (i.e. with-

out dangling edges) and if one is inserted, it is added

to the list and then processed and correctly sewn.

Consequently, the splitting operation produces a set

of square-unit regions corresponding to the initial re-

gion.

5.2 Merging Operation

Once the splitting process is done, we need to tra-

verse all the created square-unit regions to segment

the level according to our merging criterion. Actually,

the merging operation is a global process which oper-

ates on a list of darts corresponding to the edges that

were inserted by the splitting operation. This solu-

tion was selected for optimization matter as it avoids a

complete traversal of all the regions. Each edge con-

tained in this list is incident to a couple of adjacent

regions (R, R

Two conﬁgurations may be encountered: simple

or multi adjacency. In the ﬁrst case, the edge is re-

moved if the merging criterion is satisﬁed for (R, R

)

(Figure 9.A). In case of multi-adjacency, R and R

share several edges. If the merging criterion deter-

mines that (R, R

) must be merged, all the shared

edges have to be removed (Figure 9.B). Algorithm 4

details the whole process:

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

168

Figure 9: Conﬁgurations encountered during the merging

operation between two adjacent regions. (A) Simple ad-

jacency between (R

, R

) and (R

, R

): the corresponding

edges (1, 2) and (3, 4) are removed if the merging criterion

is veriﬁed. (B) Multi-adjacency between (R

, R

): if (1, 2)

has been removed, (3, 4) is removed independently of the

merging criterion.

Algorithm 4: Merging operation.

Data: A list of darts corresponding to all the1

edges inserted on G

during splitting

operation.

Result: G

segmented according to merging

criterion.

foreach dart d ∈ list do

if R(d) = R(β

(d)) or merging2

criterion(R(d), R(β

(d)))is true then

Turn off getLinel(d) (geometry);3

Relabel the darts of R(β

(d));4

Remove d and β

(d) (topology);5

• L.1: This list allows to traverse the regions created

by the splitting operation instead of traversing the

whole map. Note that we only need to store one

dart d per edge (the second one is β

(d));

• L.2: The ﬁrst condition aims to detect cases of

multi-adjacency. The merging criterion is a test

between two adjacent regions along the current

edge (i.e. (d, β

(d)));

• L.3: Let the geometry know that the linel is not

active any more;

• L.4: This step updates the darts previously com-

posing R(β

(d)) as now belonging to R(d);

• L.5: Removal of the two darts, according to the

method in (Damiand and Lienhardt, 2003).

The only constraint applied to the splitting and

merging operations is to preserve the causality of the

structure: merging is thus restricted to the basic re-

gions generated by the split of a same region. There-

fore, within these regions, our merging operation is

unrestricted and may group into a single region, any

connected set of pixels. Any partition of the initial

region may thus be encoded by our split and merge

process. Contrary to quadtrees, our splitting opera-

tion is independent of any geometrical constraint.

6 RESULTS AND ANALYSIS

This top-down model has been implemented in C++

and results have been computed on a personal com-

puter with a CPU AMDX2 3800+ (2GHz) and 1Gb

of RAM on a Linux system.

A B C D

Figure 10: Visualization of the top-down construction pro-

cess: ﬁrst row is the original image followed by levels G

and G

is a single region). Segmentations are based

on user-deﬁned thresholds (A,D) or rely on the standard de-

viation of the parent region (B,C).

The splitting and merging criteria used to obtain

the different segmentations in Figure 10 are deﬁned as

follow: let (R, R

) a couple of adjacent regions, M, m

and A denoting the maximum, minimum and average

gray level of R. The symbol tr denotes the threshold

used by the merging criterion.

In Figure 10.A and D, the merging criterion is a

comparison between the average gray levels of two

adjacent regions: (R, R

) is merged if |A − A

| < tr. In

Figure 10.B and C, tr is proportional to the standard

deviation of the parent region of (R, R

): the more ho-

mogeneous a parent region is, the more our segmen-

tation algorithm will search for ﬁne details within its

sons.

The splitting criterion avoids regions with less

than ≤ 10 pixels and those which are going to be

“completely” merged: R is split if M − m > tr. In

Figure 10.A and D, the values of tr are respectively

A TOP DOWN CONSTRUCTION SCHEME FOR IRREGULAR PYRAMIDS

169

set to 80/40/20 and 100/40/10 for the levels G

of the images Lena and Boat. Our splitting and merg-

ing operations are independent of any speciﬁc criteria:

more elaborated ones, using geometrical, colorimet-

ric or topological features, may be designed without

modifying our model.

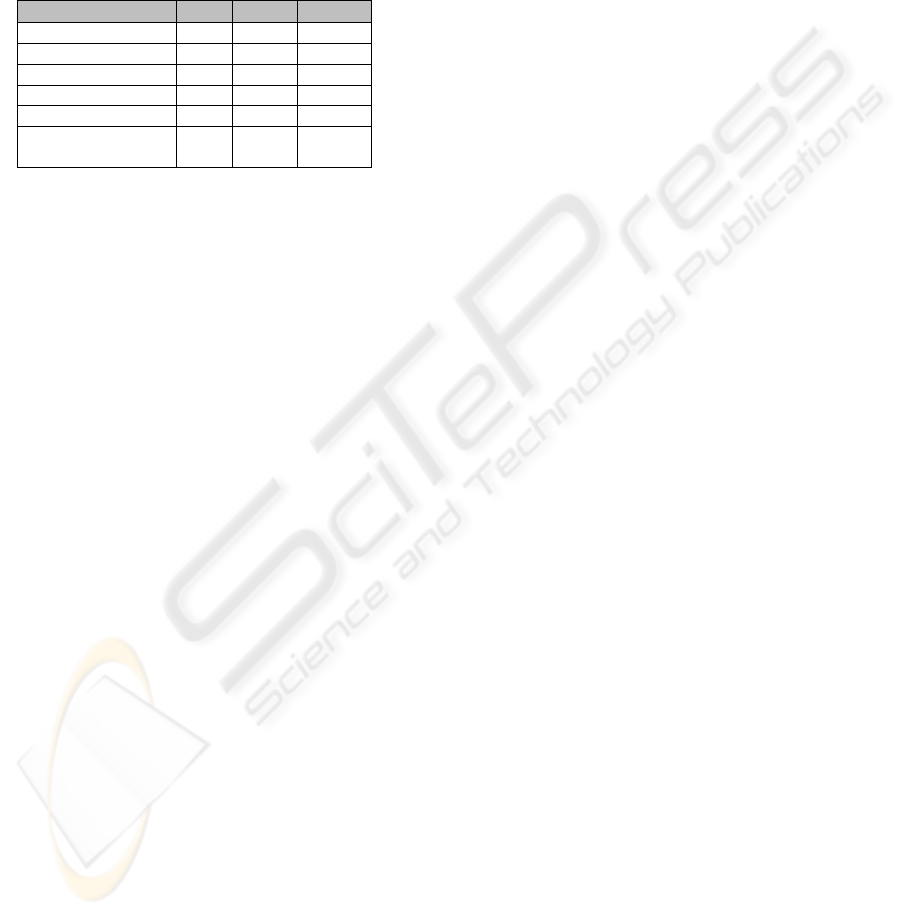
Table 2: Statistics of the top-down construction from the

image of Lena (512*512) in Figure 10.B.

darts 600 7 728 19 090

regions 134 1 624 3 953

total memory (Kb) 306 808 1 604

splitting (s) 2.23 1.42 1.29

merging (s) 0.37 0.27 0.27

total level

3.11 2.05 1.94

construction (s)

Table 2 gives the number of elements, the mem-

ory usage and processing times for each topological

map composing the pyramid of the image Lena. The

number of darts and regions strongly increases from

a level to another as the merging threshold differenti-

ates more regions. It directly impacts the memory size

of the associated topological map. Indeed, the topol-

ogy of a map requires most of the memory, except for

low segmented maps where geometry could require

more. The construction time of a level remains con-

stant because, although more regions are split, they

are smaller in number of pixels.

7 CONCLUSIONS

This paper deﬁnes a model of top-down hierarchical

data structure based on topological maps. Topologi-

cal maps are based on three models: a combinatorial

map encoding multiple adjacency of regions, an ex-

plicit encoding of the geometry of the regions border

and an encoding of the inclusion relationships. Such

a model provides a complete description of a partition

and is adapted to splitting operations. Our top-down

pyramid is based on an initial topological map suc-

cessively reﬁned by splitting operations.

This structure is particularly well suited for appli-

cations in segmentation that process large images: a

top-down construction scheme allows to store, at each

step of the algorithm, only the currently split regions

and we avoid the storage of very ﬁne partitions (ﬁrst

levels of bottom-up irregular pyramids). Besides, can

use global properties of upper levels to reﬁne the seg-

mentation in lower levels and we retrieve the dual re-

lation between quadtrees and matrix pyramids with

top-down and bottom-up approaches.

In our future work, we plan to study different en-

coding of the geometry and of the inclusion relation-

ships of topological maps. We also plan to use other

splitting methods such as (Brun et al., 2003) and to

compare our results with results obtained from other

kinds of pyramids. Finally, we should deﬁne segmen-

tation operations which fully exploit the top-down

structure of the pyramid.

REFERENCES

Bister, M., Cornelis, J., and Rosenfeld, A. (1990). A criti-

cal view of pyramid segmentation algorithms. Pattern

Recognition Letter., 11(9):605–617.

Brun, L. and Kropatsch, W. (2003). Combinatorial pyra-

mids. IEEEICIP, 2:33–37.

Brun, L. and Kropatsch, W. (2006). Contains and inside

relationships within combinatorial pyramids. Pattern

Recognition., 39(4):515–526.

Brun, L., Mokhtari, M., and Domenger, J. P. (2003). Incre-

mental modiﬁcations on segmented image deﬁned by

discrete maps. Journal of Visual Communication and

Image Representation, 14:251–290.

Damiand, G., Bertrand, Y., and Fiorio, C. (2004). Topolog-

ical model for two-dimensional image representation:

deﬁnition and optimal extraction algorithm. Computer

Vision and Image Understanding, 93(2):111–154.

Damiand, G. and Lienhardt, P. (2003). Removal and

contraction for n-dimensional generalized maps. In

DGCI, pages 408–419, Naples, Italy.

Dyer, R., Rosenfeld, A., and Hanan, S. (1980). Region rep-

resentation: Boundary codes from quadtrees. ACM:

Graphics and Image Processing, 23(3):171–179.

Guigues, L., Cocquerez, J. P., and Men, H. (2006). Scale-

sets image analysis. Comput. Vision, 68(3):289–317.

Jolion, J.-M. and Montanvert, A. (1992). The adaptative

pyramid: A framework for 2d image analysis. CVGIP,

55(3):339–348.

Jolion, J.-M. and Rosenfeld, A. (1994). A Pyramid Frame-

work for Early Vision: Multiresolutional Computer

Vision. Kluwer Academic Publishers, Norwell, MA,

USA.

Lienhardt, P. (1989). Subdivision of n-dimensional spaces

and n-dimensional generalized maps. In Sympo-

sium on Computational Geometry, pages 228–236,

Saarbr

ucken, Germany.

Meer, P. (1989). Stochastic image pyramids. CVGIP,

45:269–294.

Montanvert, A., Meer, P., and Rosenfeld, A. (1991). Hi-

erarchical image analysis using irregular tessellations.

IEEETPAMI, 13(4):307–316.

Simon, C., Damiand, G., and Lienhardt, P. (2006). nd gener-

alized map pyramids: deﬁnition, representations and

basic operations. Pattern Recognition, 39(4):527–538.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

170