
ROBUSTNESS OF DIFFERENT FEATURES FOR ONE-CLASS
CLASSIFICATION AND ANOMALY DETECTION IN WIRE ROPES
Esther-Sabrina Platzer, Joachim Denzler, Herbert S¨uße
Chair for Computer Vision, Friedrich Schiller University of Jena, Ernst-Abbe-Platz 2, 07743 Jena, Germany
Josef N¨agele, Karl-Heinz Wehking
Insitute for Mechanical Handling and Logistics, University of Stuttgart, Holzgartenstrae 15B, 70174 Stuttgart, Germany
Keywords:
Anomaly detection, Novelty detection, One-class classification, Linear prediction, Local binary pattern.
Abstract:
Automatic visual inspection of wire ropes is an important but challenging task. Anomalies in wire ropes
usually are unobtrusive and their detection is a difficult job. Certainly, a reliable anomaly detection is essential
to assure the safety of the ropes. A one-class classification approach for the automatic detection of anomalies
in wire ropes is presented. Different well-established features from the field of textural defect detection are
compared to context-sensitive features extracted by linear prediction. They are used to learn a Gaussian
mixture model which represents the faultless rope structure. Outliers are regarded as anomaly. To evaluate
the robustness of the method, a training set containing intentionally added, defective samples is used. The
generalization ability of the learned model, which is important for practical life, is exploited by testing the
model on different data sets from identically constructed ropes. All experiments were performed on real-life
rope data. The results prove a high generalization ability, as well as a good robustness to outliers in the training
set. The presented approach can exclude up to 90 percent of the rope as faultless without missing one single
defect.
1 INTRODUCTION
Wire ropes are used in many fields of logistics. They
are deployed as load cable for bridges, elevators and
ropeways. This implies a high strain by external pow-
ers every day. Unfortunately, this can lead to struc-
tural anomalies or even defects in the rope formation.
A defectiverope bears a high risk for human life. This
motivates the strict rules summarized in the European
norm (EN 12927-7, 2004), which instruct a regular
inspection of wire ropes .
Risky defects, prominent in wire ropes, are small
wire fractions, missing wires, and damaged rope ma-
terial due to lightening strokes. Furthermore, struc-
tural anomalies caused by interweavement of the rope
ends or a reduced stress are also in the focus of in-
terest. In figure 1, two exemplary defects are marked
in the rope. Visual inspection of wire ropes is a diffi-
cult and dangerous task. Besides, the inspection speed
is quite high (on average 0.5 meters/second) which
makes it a hard effort, to concentrate on the passing
rope without missing small defective rope regions.
Figure 1: Rope defects: in the upper image you can see a
wire fraction and in the image below a wire is missing.
A prototypic acquisition system was developed to
overcome these limitations (Moll, 2003). Four line
cameras record the passing rope and yield four differ-
ent views. By this, the rope can be inspected in the
office without time pressure. The images in figure 1
were acquired with this system.
Defects and anomalies in wire ropes are unimposing
171
Platzer E., Denzler J., Süße H., Nägele J. and Wehking K. (2009).
ROBUSTNESS OF DIFFERENT FEATURES FOR ONE-CLASS CLASSIFICATION AND ANOMALY DETECTION IN WIRE ROPES.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 170-177
DOI: 10.5220/0001783801700177
Copyright
c
SciTePress

and small. The image quality is deranged by mud,
powder, grease or water and the lighting conditions
change frequently. Therefore, the choice of features
for the detection task is important. Recent approaches
for defect or anomaly detection focus on fault de-
tection in material-surfaces. In (Platzer et al., 2008)
we introduced a one-class classification approach for
anomaly detection in wire ropes using linear predic-
tion (LP) coefficients as features and a Gaussian mix-
ture for model learning. The former work is ex-
tended in this paper by two main aspects: the per-
formance of LP features is compared to that of other
well-established features from the field of textural de-
fect detection, and the robustness to outliers in the
training set as well as the generalization ability of
the presented approach are carefully evaluated. The
last point is of particular interest for the practical rel-
evance of the method.
Features based on local binary patterns (LBP)
were first introduced by Ojala (Ojala et al., 1996)
for texture classification. Recently they were used
for defect detection in fabrics (Tajeripour et al.,
2008) and for real-time surface inspection (M¨aenp¨a¨a
et al., 2003). Textural features, extracted from co-
occurrence matrices, were proposed by Harlick in
the early 70’s (Harlick et al., 1973) and are fre-
quently used for texture description (Chen et al.,
1998). (Iivarinen, 2000) compares two histogram-
based methods for surface defect detection using LBP
and co-occurrence matrices. (Rautkorpi and Iivari-
nen, 2005) used shaped-based co-occurrence matrices
for the classification of metal surface defects. (Vartia-
ninen et al., 2008) focus on the detection of irregular-
ities in regular, periodic patterns. They separate the
image data in a regular and an irregular part. Based
on the resulting irregularities, we compute local his-
tograms, which serve as features. Another important
category of features for texture analysis and textural
defect detection are wavelet-based features. (Kumar
and Pang, 2002) for example use Gabor features for
the detection of defects in textured material. How-
ever, the computation of these features requires large
filter banks and high computational costs. Due to
the huge size of rope data sets (20-30 GB) the time-
consuming computation of Gabor features seems to
be not the best choice. In (Varma and Zisserman,
2003) the authors state, that similar results to that
obtained by the usage of wavelet features can be re-
solved with help of joint neighborhood distributions
and less computational effort.
The one-class classification strategy proposed in
(Platzer et al., 2008) was chosen due to a lack of de-
fective training samples for supervised classification.
In contrast, it is no problem to design a huge sample
set of faultless training samples. With this faultfree
training set a model of the intact rope structure can
be learned and in the detection step outliers with re-
gard to this model are classified as defect. However,
the only available ground truth information about this
training data is the labeling of the human expert. In
the following,there remains a small uncertainty of un-
derdiagnosed defects in the training set. For this rea-
son the robustness of the proposed method to outliers
in the training set is evaluated. Results obtained by
learning from a faultless training set are compared to
those, obtained by learning from a training set with
intentionally added, faulty samples. The generaliza-
tion ability of a learned model is a further important
point, especially for the practical relevance of the pre-
sented method. There exist only a limited number of
different construction types for wire ropes. The dif-
ferences between them are mainly a different num-
ber of wires and strands, different thickness of single
wires, the length of twist and the diameter. If just one
model for every possible rope type would have to be
learned in advance, this would save a lot of compu-
tational effort. However, the rope data from different
ropes differs significantly due to the changing acquisi-
tion conditions and a different mounting of the ropes.
Nevertheless, it is desirable to have just one model
for every construction type and to overcome the chal-
lenges of a changing acquisition environment. There-
fore, the generalization ability of the learned models
is evaluated by learning and testing on different rope
data from nearly identical constructed ropes.
The paper is structured as follows: in section 2 we
briefly review the feature extraction using linear pre-
diction and give a description of the used textural fea-
tures and their extraction. The one-class classification
of wire rope data is shortly summarized in section 3.
Experiments, revealingthe usability and robustness of
our approach, have been performed on real-life rope
data and results are presented in section 4. A conclu-
sion and a discussion about future work is given in
section 5.
2 FEATURE EXTRACTION
In this section the different features are briefly re-
viewed. Their extraction from the underlying rope
data is described, as it differs for the LP features in
contrast to the remaining features. In the following, a
short motivation for the different features used in this
context, is given.
Local binary patterns (LBP) code the local
graylevel-structure of a pixel neighborhood. His-
tograms based on the resulting codes lead to a local
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
172

feature distribution. Since local binary patterns incor-
porate contextual information from a local neighbor-
hood, a comparison of their performance with that of
the LP features is of particular interest.
(Harlick et al., 1973) introduced a set of 14 dif-
ferent textural features computed from co-occurrence
matrices. They reveal the spatial distribution of gray-
levels an though seem to be an interesting choice for
structures with a certain regularity, like wire ropes.
The detection of irregularities, proposed in (Var-
tianinen et al., 2008) focuses on anomalies in regular,
periodic patterns. Since the structure of wire ropes
is not perfectly periodic, but offers some regular pe-
riodicities, we used the detected irregularities for the
computation of local, histogram-based features.
2.1 Linear Prediction Based Features
Linear prediction can be seen as one key technique in
speech recognition (Rabiner and Juang, 1993). It is
used to compute parameters determining the spectral
characteristics of the underlying speech signal.
The behavior of the underlying signal is modelled
by forecasting the value x(t) of the signal x at time t
by a linear combination of the p past values x(t − k)
with k = 1, . . . , p, where p is the order of the autore-
gressive process. The prediction ˆx(t) of a 1-D signal
can be written as
ˆx(t) = −
p
∑
k=1
α
k
x(t − k) (1)
with the following prediction error
e(t) = x(t) − ˆx(t) = x(t) +
p
∑
k=1
α
k
x(t − k). (2)
This motivates the choice of linear prediction for fea-
ture extraction. For the prediction of the actual value
the contextual information of the past values is used
and is implicitly incorporated in the resulting feature.
Based on a least-squares formulation, the opti-
mal parameters
~
α = (1, α
1
... α
p
) can be obtained by
solving the normal equations (Makhoul, 1975). The
optimal coefficients are derived by use of the auto-
correlation method and the Levinson-Durbin recur-
sion (Makhoul, 1975; Rabiner and Juang, 1993). Free
parameters of this method are framesize and the order
of the process. In experiments the optimal framesize
was found to be 20 camera lines with an incremen-
tal overlap of 10 lines. Best results were achieved for
order p = 8.
Rope data, obtained from the acquisition system,
can be seen as a sequence of 2-d images. Thus,
with 1-d linear prediction it is not possible to ana-
lyze the 2-d signal. To overcome this, the rope data
Figure 2: Multichannel version of the classification model.
For every channel (horizontal white boxes) a feature is ex-
tracted and examined in a separate feature space. The ver-
tical white box marks the signal values, which are actually
predicted.
is considered as a multichannel time series. The sig-
nal ~x consists of c channels ~x = (~x
1
~x
2
...~x
c
)
T
and
every channel represents a 1-dimensional time se-
ries ~x
i
(t) = (x
i
(1),... , x
i
(t)). For every channel i of
this signal an individual 1-d linear prediction is per-
formed, leading to the estimate ˆx
i
(t), the squared pre-
diction error for the whole frame, and the coefficient
vector
~
α
i
. These components are used as correspond-
ing feature for the actual frame and the channel i. Best
results were obtained with a combined feature vector,
including prediction coefficients and the squared er-
ror. In the training step, a separate model for every
channel is learned. This is schematically depicted in
figure 2. By this, the different appearance of the rope
at different positions in the images is taken into con-
sideration.
2.2 Local Binary Pattern
For the local binary pattern (LBP) a texture region is
seen as a joint distribution of P + 1 pixel-graylevels
in a predefined neighborhood. Often a circular neigh-
borhood with radius R and P equally spaced sam-
ples is chosen. The center pixel grayvalue g
c
serves
as threshold for the binarization of the neighborhood
pixels g
p
, p = 1, . . . , P. The local binary pattern oper-
ator can be summarized as follows:
LBP
P,R
(g
c
) =
P
∑
p=1
s(g
p
− g
c
)2
p−1
(3)
with s(x) =
(
1, x ≥ 0
0, x < 0 .
(4)
Transforming the binary vector into a decimal num-
ber (3) results in a pixel label, based on the neigh-
borhood information. (Ojala et al., 2000) developed a
rotational invariant and uniform extension of the local
binary pattern. For the anomaly detection task there
is no need for rotational invariance due to the constant
rope orientation. The uniformity of the pattern is de-
fined based on the number of 0/1 transitions U in the
binary vector. The resulting LBP code is computed as
ROBUSTNESS OF DIFFERENT FEATURES FOR ONE-CLASS CLASSIFICATION AND ANOMALY DETECTION
IN WIRE ROPES
173

Figure 3: Detection window with 20× 20 pixels in relation
to the wire rope image data.
follows:
LBP
u
P,R
(g
c
) =
(
∑
P
p=1
s(g
p
− g
c
), U ≤ 2
P+ 1, otherwise .
(5)
A histogram with a predefined number of bins is built
from the underlying code distribution and serves as
feature. The optimal parameters P and R and the
number of quantization levels for the local histograms
were determined in extensive experiments. We found
the optimal parameter setting to be R = 1, P = 8 with
16 quantization levels for the histogram. As already
mentioned, defects usually have just a small elonga-
tion. Hence, the histogram computation resulting in
the feature vector is done for a small detection win-
dow (20× 20 pixels), which moves over the underly-
ing frame of rope data. To get an impression of the
window size in relation to the rope data, a detection
window is visualized in figure 3. By this, more than
one feature is obtained for every frame.
2.3 Co-occurrence Features
Features for texture classification based on co-
occurrence matrices were first introduced by (Harlick
et al., 1973). A co-occurrence matrix is defined with
respect to a certain displacement vector
~
d = (d
x
,d
y
)
and results in the joint distribution of co-occurring
grayvalues. The relative frequency p
ij
, which de-
fines the co-occurrence of two neighboring grayval-
ues (with respect to
~
d) i and j, is defined as
p
ij
(
~
d) = λ|{(x,y) : I(x, y) = i, I(x+ d
x
,y+ d
y
) = j} |
(6)
with i, j ∈ {0. . . G − 1} and G the number of gray lev-
els. I represents an image of size M × N and λ is a
normalization factor such that
∑
ij
p
ij
(
~
d) = 1.
Harlick introduced 14 different textural features
(Harlick et al., 1973). Experiments for the determina-
tion of the most discriminative ones were performed.
As the information theoretic texture features named
difference entropy, information measure one, infor-
mation measure two and the maximum correlation
coefficient lead to the best results, a combination of
these four features is used. Furthermore, a displace-
ment vector of 2 pixels length with an angle of 90
degrees has led to the best results in our tests with
varying parameters. As co-occurrence matrices lead
to a global representation of the underlying texture,
they are usually computed for a local region of inter-
est. For the detection of small, regional anomalies in
the rope structure this is important, as the small defect
will not be recognized with global features. Again,
a detection window of 20 × 20 pixels was used for
the computation of the co-occurrencematrices and the
following feature computation.
2.4 Features based on Pattern
Irregularity
(Vartianinen et al., 2008) describe an approach for the
detection of irregularities in regular patterns based on
the Fourier transform. Regular patterns result in dis-
tinct frequency peaks in the Fourier domain. By fil-
tering out these frequencies and transforming the data
back to the spatial domain, a perfectly regular pattern
can be obtained. On the other hand, it is possible to
substract this regular part from a unit function in the
frequency domain, which results in the irregular part
of the pattern:
I(x,y) = F
−1
(I(u,v)) (7)
= F
−1
((1− M(u,v) + M(u, v))I(u,v)) (8)
= F
−1
(M(u,v)I(u,v))
| {z }
regular part
(9)
+ F
−1
((1− M(u,v))I(u,v))
| {z }
irregular part
I(x,y) is the input image, I(u, v) is the Fourier trans-
formed image, F is the Fourier transform and M(u, v)
is the filter function in the frequency domain. 1 rep-
resents the unit function. Without prior knowledge
about the pattern structure a reasonable filter func-
tion is self-filtering (Bailey, 1993). Filtering is per-
formed with the magnitude of the Fourier spectrum
M(u,v) = |I(u, v)|. As the rope consists of regular
structures, filtering is done with regard to the irregu-
lar part of the data. For the computation of the local
histograms again a detection window of size 20 × 20
is used. Experimental evaluation of the used quanti-
zation levels for histogram computation showed, that
a histogram with 16 bins performed the best.
3 ONE-CLASS CLASSIFICATION
In order to exclude as many rope meters as possible
from further inspection, the theory of one-class clas-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
174

sification seems to be a good choice. A separation be-
tween faultless and faulty samples is required. In this
case, the faultless samples represent the target class
ω
T
and the defects are considered as outliers ω
O
. As
it is no problem to construct a large training set of
defect-free feature samples, a representation for this
target density p(~x | ω
T
) has to be found without any
knowledge about the outlier density p(~x | ω
O
) (Tax,
2001). Here,~x is the feature vector.
For one-class classification problems the false
negative rate (FNR) is the only rate which can be
measured directly from the training data. The false
positive rate (FPR) is the most important measure for
defect detection, but cannot be obtained without a
sample set containing a sufficient number of defective
samples. In case of a uniform distributed outlier den-
sity, however, a minimization of the FNR in combina-
tion with a minimization of the descriptive volume of
the target density p(~x | ω
T
) results in a minimization
of the FNR and FPR (Tax, 2001).
There exist many different methods for one-class
classification (also called novelty detection) (Hodge
and Austin, 2004; Markou and Singh, 2003). In
(Platzer et al., 2008) two approaches, namely the
K-means clustering and a Gaussian mixture model
(GMM), were compared. In contrast to our former
work, where the training sample set contained only
faultless samples, the learning step is now modified.
Model learning is performed on a sample set with in-
tentionally included samples from defective rope re-
gions. The aim is to evaluate the robustness of the
method against outliers in the training set. This would
reduce the need of a human inspector,who determines
an optimal, faultfree rope region for model learning.
3.1 Decision Making
For a classification into target class and outliers, a
threshold is defined on the density. This threshold
is based on the mean and the minimal probability
reached in the training. It is stated, that an optimal
threshold should be within the range of mean and
minimum probability. As the training samples are all
considered as defect-free, the minimum probability
gives the lower bound for the likelihood of faultless
samples. To account for possible outliers, the thresh-
old is varied in this range and the evaluation is done
by means of receiver operating characteristics (ROC).
Since anomaly detection is a security relevant applica-
tion, it is important not to miss any defect. As a con-
sequence, the optimal threshold maximizes the TPR
(number of samples correctly classified to the target
class) while keeping the FPR zero.
Due to feature extraction with a detection win-
Figure 4: In this rope region a wire is missing. The window
marks the frame, which was detected as an outlier by the
described system.
dow (or in case of the LP features based on one sin-
gle channel), a rope frame consists of more than one
feature. Accordingly, the decision for the overall
frame is based on the decisions for the single win-
dows/channels. In case of feature extraction by a de-
tection window, the frame is classified as outlier, if
one of the corresponding windows is rejected as out-
lier. For the channel-based LP features a further pre-
processing is necessary. As the channels have no spa-
tial extension like the detection window, one single
channel is prone to noise. Therefore, a local channel-
neighborhoodconsisting of 15 channels is scanned for
potential outliers and only if the number of channel-
votes exceeds five channels, the whole frame is re-
jected as defect.
Since a defect usually lasts over several frames,
the whole defect is regarded as detected, if one frame
in this range is rejected as outlier. Consequently, de-
fects are detected but not localized at the moment.
Figure 4 displays one defect, detected by the de-
scribed system. The borders of the frame, detected
as outlier are depicted by the window.
4 EXPERIMENTS AND RESULTS
In the following section experiments and their out-
comes are presented. All experiments were per-
formed on authentic rope data, acquired from real
ropeways. In the generalization experiment (subsec-
tion 4.3) the data used for model learning was ac-
quired in a controlled environment, but testing was
again performed on data from a real ropeway. Model
learning was done with a Gaussian mixture composed
of five mixture components and rope data belonging
to one of the four views. Testing was performed on
all four views and the resulting ROC curves were av-
eraged over the different views. Interference between
the views was not yet considered. The length of the
used rope regions in all experiments is given by the
number of camera lines, followed by the correspond-
ing length in meters put into brackets. Learning on
20.000 camera lines (2m rope) of one view takes be-
tween 25 seconds and one minute on a Intel Pentium
ROBUSTNESS OF DIFFERENT FEATURES FOR ONE-CLASS CLASSIFICATION AND ANOMALY DETECTION
IN WIRE ROPES
175
4 with 3,4GHz, according to the choice of features.
Surely, the LP model learning needs the most time
due to the separate computation of one model for ev-
ery channel. A testrun on 600.000 (60m rope) lines
takes approximately between 14 (Irregularity) and 25
minutes (LP) per view, which gives an average de-
tection speed of 14 till 23 seconds per meter of rope
(10.000 camera lines). Again the computation time
depends on the choice of features.
4.1 Comparison of Features
To compare the performance of the different features,
model learning was done for every feature on the
same training set, consisting of 20.000 lines (2m rope)
of defect-free rope data from a real ropeway. Experi-
ments were performed on a connected region of rope
data, containing 600.000 camera lines (60m rope) and
covering all known defects in the rope. The receiver
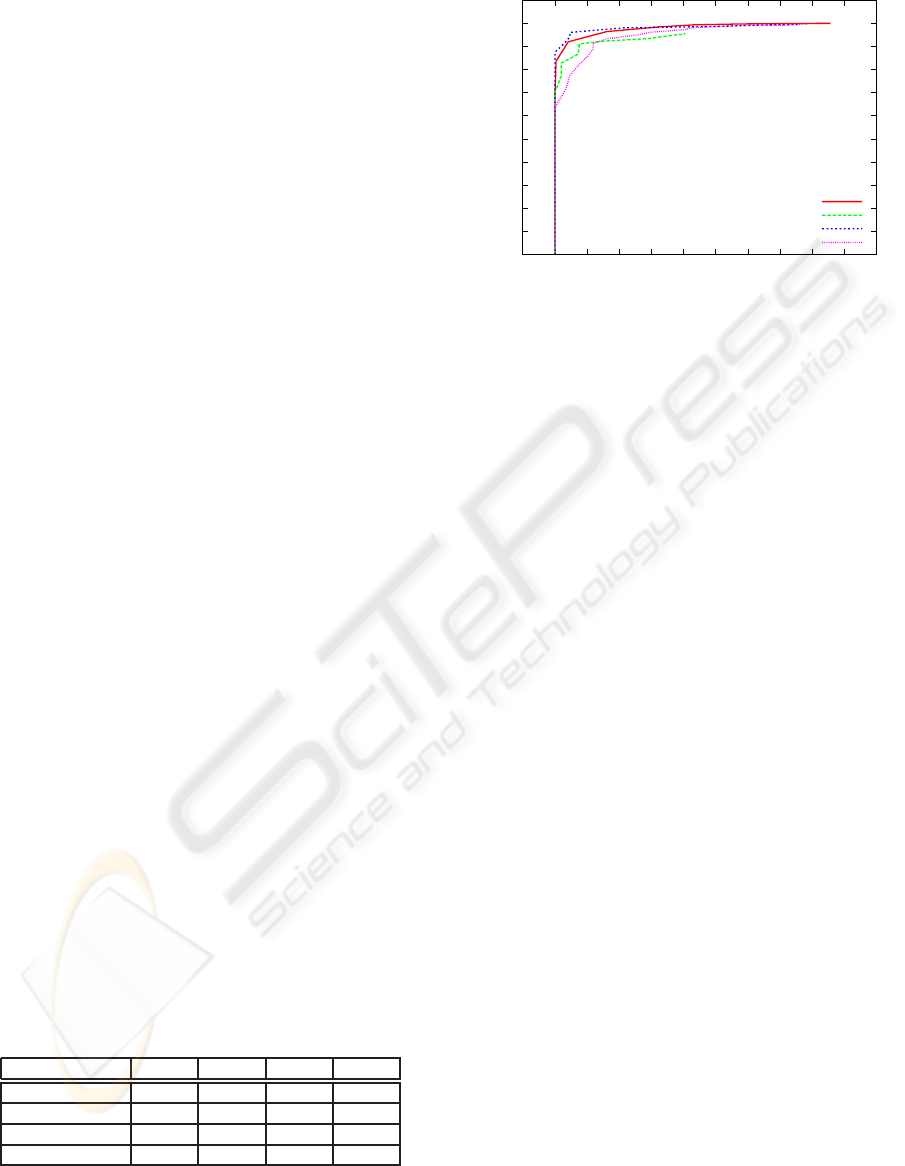
operating characteristics in figure 5 point out, that the
LBP features outperform all other features. However,
for all used features respectable results were obtained.
Features based on detected irregularities perform the
worst. A lot of noise is contained in the rope raw
data and the structure is not perfectly regular, so that
a certain amount of irregularities are detected in every
frame. This results in a less discriminative behavior.
Context-sensitive features like the LP features and the
LBP features perform the best. Their overall charac-
teristics show a more robust behavior. Table 1 sum-
marizes the maximum TPR for every view and fea-
ture, which was reached for a FPR of zero. The rea-
son for the decreased TPR of the LP features in view 4
is an easily missed defect in this single view. The un-
derdiagnosed error was manually inspected and it was
discovered, that this defect is spread over more than
one view. In the remaining views this defect was dis-
covered correctly. From this it can be educed, that in-
terference between the different views could be a pos-
sibility to eliminate this misclassifications. In sum-
mary, these results reveal the importance of context-
sensitive features for the challenging task of defect
detection in wire ropes.
Table 1: Comparison of the maximum TPR for a FPR of
zero for all features and all views.
Featuretype view1 view2 view3 view4
LP 0.96 0.93 0.94 0.62
Co-occurrence 0.78 0.77 0.77 0.88
LBP 0.96 0.82 0.88 0.93
Irregularity 0.62 0.89 0.71 0.78
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
True Positive Rate
False Positive Rate
LP
Co-occurrence
LBP
Irregularity
Figure 5: Comparison of the ROC curves for the different
choice of features.
4.2 Robustness to Outliers
To evaluate the robustness to outliers in the train-
ing set, model learning was performed on a training
set containing 200.000 (20m rope) lines of rope data.
For learning, the view containing the most defects (9
defects) was chosen. Testing was performed on the
remaining three views, also containing each at least
seven defects. For comparison, the same experiment
was performed with a model, learned from 200.000
defect-free camera lines (20m rope). The resulting
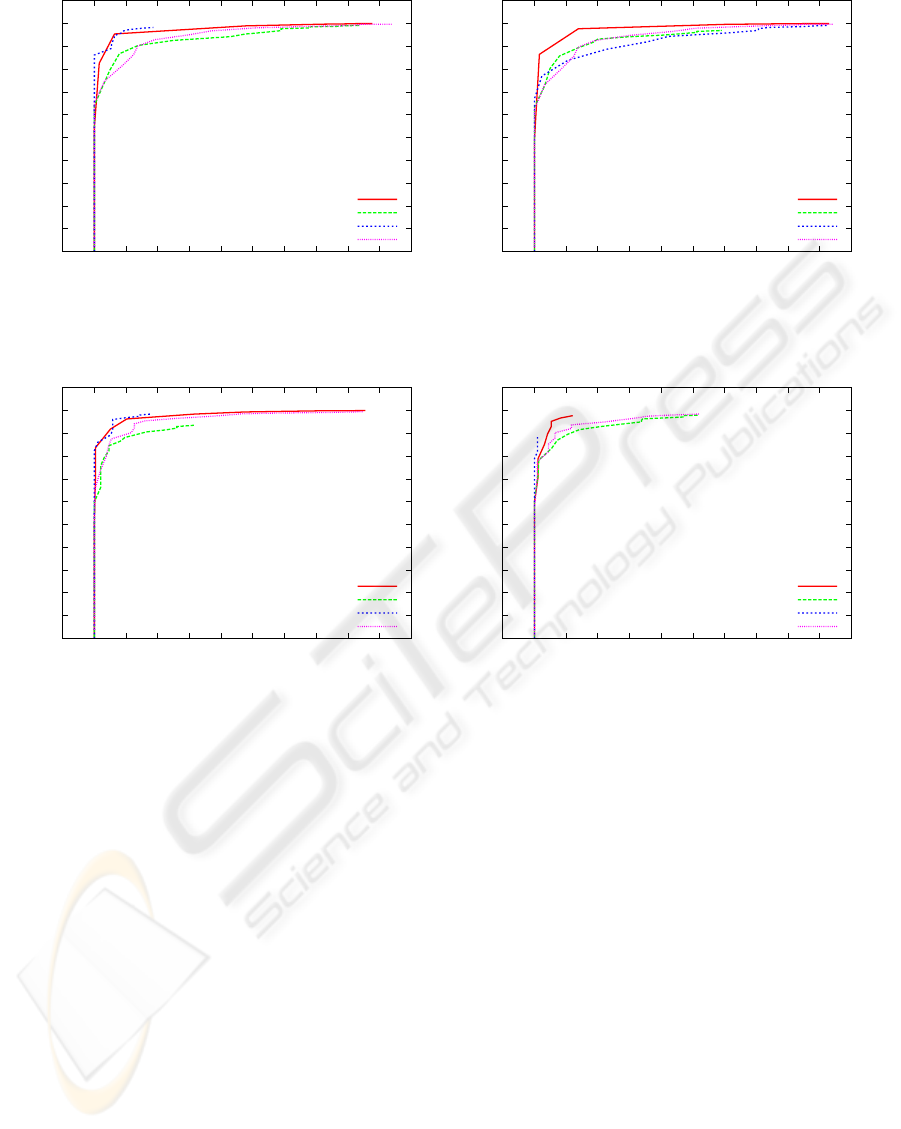
ROC curves are compared in figure 6. The ROC curve
in figure 6(a) gives the averaged ROC for the model,
learned on defect-free training data. Figure 6(b) vi-
sualizes the results obtained with a model, learned
from a training set including outliers. Obviously, the
method is robust to few outliers in the training set,
as the results differ not significantly from each other.
Where the LP features show the most robust behavior,
the LBP features seem to be error-prone if outliers are
contained in the training set. The size of the training
set was increased in the experiment, to incorporate as
many defects as possible.
4.3 Generalization Ability
For the evaluation of the generalization ability, learn-
ing was performed on a real, faultless rope, acquired
in a controlled environment. Testing on the other hand
was performed on different rope data from a real rope-
way containing defective regions. Both ropes belong
to the same construction type and they only differ in
their diameter by 10 pixels. In figure 7 the results are
depicted by the corresponding ROC curves, averaged
over all views. Figure 7(a) is generated by learning
and testing on the same rope from the ropeway and
figure 7(b) shows the result for learning in the con-
trolled setup and testing on real-life rope data. In both
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
176
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
True Positive Rate
False Positive Rate
LP
Co-occurrence
LBP
Irregularity
(a)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
True Positive Rate
False Positive Rate
LP
Co-occurrence
LBP
Irregularity
(b)
Figure 6: Comparison of ROC curves for learning with a defect-free training set (a) and a training set including defects (b).
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
True Positive Rate
False Positive Rate
LP
Co-occurrence
LBP
Irregularity
(a)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
True Positive Rate
False Positive Rate
LP
Co-occurrence
LBP
Irregularity
(b)
Figure 7: Comparison of the ROC curves for learning and testing on the same data set (a) and learning and testing on two
different, identically constructed rope data sets (b).
cases the size of the learning set was 20.000 camera
lines (2m rope). The LBP features obviously show
the best generalization performance. The decreased
performance of the LP features again is caused by
a missed defect in one single view, which neverthe-
less was correctly discovered in the other views. Co-
occurrence features as well as irregularity-based fea-
tures show a surprising good generalization perfor-
mance. In general, these results indicate a quite good
generalization ability of the overall approach.
5 DISCUSSION AND OUTLOOK
We presented important and meaningful extensions
of our former work. The one-class classification
approach for anomaly detection in wire ropes, pre-
sented in (Platzer et al., 2008), was extended by three
well-established features from the field of textural
defect detection, and their performances were com-
pared. The results emphasize the necessity of context-
sensitive features for this challenging task. Although
all compared features result in a good performance,
the overall behavior of the context-sensitive features
is better. With the presented approach 70 till 90 per-
cent of the rope can be excluded from a reinspection
by a human expert and only a region of 10 cm around
a detected defect has to be re-examined again. Exper-
iments emphasizing the robustness and generalization
ability of the approach were presented. They pointed
out that a perfect, faultless training set is not essen-
tial for model learning. Especially from the practical
point of view, this is an important improvement, pre-
cisely because one cannot assure a completely defect-
free training set. With regard to the generalization
ability, the learned model was evaluated on real-life
rope data of different, individual ropes, which belong
to the same construction type. Results indicate a good
ROBUSTNESS OF DIFFERENT FEATURES FOR ONE-CLASS CLASSIFICATION AND ANOMALY DETECTION
IN WIRE ROPES
177

generalization ability of learned models with respect
to ropes, which are constructed in the same way. In
the context of practical applicability this is a remark-
able improvement, as it is a difficult and time consum-
ing task to learn an individual model of the respective
rope previous to every detection run.
In future, the focus will be turned to the defect lo-
calization. Using not only context-sensitive features,
but also incorporating them into a context-based clas-
sification could lead to a further improvement of the
system. Interference between the different views, ac-
quired by the prototype system is also an interesting
point under investigation. For both problems, hidden
Markov models seem to be a good framework.
ACKNOWLEDGEMENTS
This research is supported by the German Research
Foundation (DFG) within the particular projects DE
735/6-1 and WE 2187/15-1.
REFERENCES
Bailey, D. (1993). Frequency domain self-filtering for pat-
tern detection. In Proceedings of the first New Zealand
Conference on Image and Vision Computing, pages
237–243.
Chen, C. H., Pau, L. F., and Wang, P. S. P., editors (1998).
The Handbook of Pattern Recognition and Computer
Vision (2nd Edition). World Scientific Publishing Co.
EN 12927-7 (2004). Safety requirments for cableways in-
stallations designed to carry persons. ropes. inspec-
tion, repair and maintenance. European Norm: EN
12927-7:2004.
Harlick, R. M., Shanmugam, K., and Dinstein, I. (1973).
Textural Features for Image Classification. IEEE
Transactions on Systems, Man and Cybernetics,
3(6):610–621.
Hodge, V. J. and Austin, J. (2004). A Survey of Outlier De-
tection Methodologies. Artificial Intelligence Review,
22(2):85–126.
Iivarinen, J. (2000). Surface Defect Detection with
Histogram-Based Texture Features. volume 4197 of
Society of Photo-Optical Instrumentation Engineers
(SPIE) Conference Series, pages 140–145.
Kumar, A. and Pang, K. H. (2002). Defect Detection in
Textured Materials Using Gabor Filters. IEEE Trans-
actions on Industry Applications, 38(2):425–440.
M¨aenp¨a¨a, T., Turtinen, M., and Pietik¨ainen, M. (2003).
Real-time surface inspection by texture. Real-Time
Imaging, 9(5):289–296.
Makhoul, J. (1975). Linear Prediction: A Tutorial Review.
Proceedings of the IEEE, 63(4):561– 580.
Markou, M. and Singh, S. (2003). Novelty detection: a re-
view - part 1: statistical approaches. Signal Process-
ing, 83(12):2481 – 2497.
Moll, D. (2003). Innovative procedure for visual rope in-
spection. Lift Report, 29(3):10–14.
Ojala, T., Pietik¨ainen, M., and Harwood, D. (1996). A com-
parative study of texture measures with classification
based on featured distributions. Pattern Recognition,
29(1):51–59.
Ojala, T., Pietik¨ainen, M., and M¨aenp¨a¨a, T. (2000). Gray
Scale and Rotation Invariant Texture Classification
with Local Binary Patterns. In Proceedings of the
European Conference on Computer Vision (ECCV),
pages 404–420.
Platzer, E.-S., Denzler, J., S¨uße, H., N¨agele, J., and Wehk-
ing, K.-H. (2008). Challenging anomaly detection in
wire ropes using linear prediction combined with one-
class classification. In Proceedings of the 13th Inter-
national Fall Workshop Vision, Modeling and Visual-
ization, pages 343–352.
Rabiner, L. and Juang, B.-H. (1993). Fundementals of
speech recognition. Prentice Hall PTR.
Rautkorpi, R. and Iivarinen, J. (2005). Shape-Based Co-
occurrence Matrices for Defect Classification. In Pro-
ceedings of the 14th Scandinaian Converence on Im-
age Analysis (SCIA), pages 588–597.
Tajeripour, F., Kabir, E., and Sheikhi, A. (2008). Fabric De-
fect Detection Using Modified Local Binary Patterns.
EURASIP Journal on Advances in Signal Processing,
8(1):1–12.
Tax, D. M. J. (2001). One-Class classification: Concept-
learning in the absence of counter-examples. Phd the-
sis, Delft University of Technology.
Varma, M. and Zisserman, A. (2003). Texture Classifica-
tion: Are Filter Banks Necessary? In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), volume 2, pages 691–698.
Vartianinen, J., Sadovnikov, A., Kamarainen, J.-K., Lensu,
L., and K¨alvi¨ainen, H. (2008). Detection of irregular-
ities in regular patterns. Machine Vision and Applica-
tions, 19(4):249–259.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
178
