GENERIC

MOTION BASED OBJECT SEGMENTATION FOR

ASSISTED NAVIGATION

Sion Hannuna

Department of Computer Science, University of Bristol, Bristol, U.K.

Xianghua Xie

Department of Computer Science, University of Wales Swansea, Swansea, U.K.

Majid Mirmehdi, Neill Campbell

Department of Computer Science, University of Bristol, Bristol, U.K.

Keywords:

Uncategorised object detection, Stereo depth, Assisted blind navigation, Sparse optical ﬂow.

Abstract:

We propose a robust approach to annotating independently moving objects captured by head mounted stereo

cameras that are worn by an ambulatory (and visually impaired) user. Initially, sparse optical ﬂow is extracted

from a single image stream, in tandem with dense depth maps. Then, using the assumption that apparent

movement generated by camera egomotion is dominant, ﬂow corresponding to independently moving objects

(IMOs) is robustly segmented using MLESAC. Next, the mode depth of the feature points deﬁning this ﬂow

(the foreground) are obtained by aligning them with the depth maps. Finally, a bounding box is scaled pro-

portionally to this mode depth and robustly ﬁt to the foreground points such that the number of inliers is

maximised.

1 INTRODUCTION

This paper describe a method for isolating and an-

notating moving objects using head mounted stereo

cameras worn by an ambulatory or stationary person.

The work is carried out in the context of a large, mul-

tifaceted and EU-funded project (CASBliP

) which

aims to develop a multi-sensor system capable of in-

terpreting basic characteristics of some primary ele-

ments of interest in outdoor scenes (i.e. in city streets)

and transforming them into a sound map for blind

users as a perception and navigation aid.

One of the key tasks is to effectively detect mov-

ing objects, which may pose a danger to the user,

and estimate their distance and relative motion. Un-

like, for example, in autonomous vehicle navigation

(de Souza and Kak, 2002; Leonard, 2007), where the

camera egomotion can be estimated based on aux-

iliary measurements, e.g. using speedometers, our

cameras can undergo arbitrary motion to six degree

of freedom (dof). Such egomotion introduces sig-

www

.casblip.upv.es

niﬁcant relative motions for all objects in the scene,

which makes it difﬁcult to detect independent mov-

ing objects and even more difﬁcult in order to do so

in close to real time while simultaneously estimating

the depth. Fortunately, since the speed of the user is

much slower than that of the objects of interest, such

as a car, the translational component of the egomo-

tion can be neglected. Moreover, the user will be

aware of their own cadence and trajectory, thus ac-

curate estimates of true camera egomotion are unnec-

essary. However, it is still challenging to efﬁciently

differentiate apparent motions induced in the scene

by camera movement from that originating from real

movement in the environment.

Pauwels and Hulle (Pauwels and Hulle, 2004)

propose a M-estimator based robust approach to ex-

tracting egomotion from noisy optical ﬂow. Tracked

points whose trajectory do not originate in the focus

of expansion (FOE) are deemed to belong to indepen-

dently moving objects. This assumption fails for ob-

jects traveling in front of the camera towards the FOE.

In (Badino, 2004), a method for deducing egomotion

in a moving vehicle using a mobile stereo platform

450

Hannuna S., Xie X., Mirmehdi M. and Campbell N. (2009).

GENERIC MOTION BASED OBJECT SEGMENTATION FOR ASSISTED NAVIGATION.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications , pages 450-457

DOI: 10.5220/0001785704500457

 SciTePress

is described. They utilise a combination of 3D point

correspondences, and a smoothness of motion con-

straint to deduce vehicle motion. In (Ess et al., 2007),

the ground plane and pedestrians are simultaneously

extracted using stereo cameras mounted on a trolley.

Although they show impressive results, appearance

based detection is not sufﬁcient enough for the pur-

poses of our application. Other work that deal with

the problem of segmenting independent motion with

camera egomotion include (Rabe et al., 2007), (Yuan

et al., 2007) and (Yu et al., 2005).

Depth estimation or disparity computation is of-

ten carried out based on the assumption that depth

discontinuity boundaries collocate with intensity or

colour discontinuity boundaries. The search for this

collocation is based on intensity similarity match-

ing from one image to the other, which includes

stages such as matching cost computation and aggre-

gation, disparity computation and reﬁnement. Op-

timisation plays an important role in disparity esti-

mation (Gong and Yang, 2007). Recent comparative

studies, such as (Scharstein and Szeliski, 2002), have

shown that graph cut (Veksler, 2003) and belief prop-

agation (Felzenszwalb and Huttenlocher, 2006) are

two powerful techniques to achieve accurate disparity

maps. However, both are computationally expensive

and require hardware solutions to achieve near real

time performance, e.g. (Yang et al., 2006).

In section 2, we ﬁrst provide an overview of the

proposed method, and then elaborate each of its stages

in some subsections. Then, experimental results are

reported in section 3, followed with conclusion in sec-

tion 5.

2 PROPOSED APPROACH

The primary aim here with respect to generic object

detection is to identify objects moving independently

in the scene. We are not concerned with the speciﬁc

class of objects, but just to extract sufﬁcient informa-

tion for a later cognitive module to interpret if the mo-

tion of the object can pose a danger to the visually-

impaired user. This is achieved by tracking a sparse

set of feature points, which implicitly label moving

objects, and segmenting features which exhibit mo-

tion that is not consistent with that generated by the

movement of the stereo cameras. Sparse point track-

ing has previously been applied successfully to mo-

tion based segmentation in (Hannuna, 2007). Dense

depth maps are simultaneously extracted, yielding lo-

cations and 3D trajectories for each feature point.

These depth maps are also required for input into a

later stage of the CASBliP project (the soniﬁcation

process to generate a sound map), so they do not incur

extra computational burden compared to using sparse

depth maps.

The Kanade-Lucas-Tomasi (KLT) (Shi and

Tomasi, 1994) tracker is used to generate this sparse

set of points in tandem with the depth estimation

process. This tracker preferentially annotates high

entropy regions. As well as facilitating tracking,

this also ensures that values taken from the depth

maps in the vicinity of the KLT points are likely

to be relatively reliable as it is probable that good

correspondences have been achieved for these

regions.

Points corresponding to independently moving

objects are segmented using MLESAC (Torr and Zis-

serman, 2000) (Maximum Likelihood Sample Con-

sensus), based on the assumption that apparent move-

ment generated by camera egomotion is dominant.

Outliers to this dominant motion then generally cor-

respond to independently moving objects. Bounding

boxes are ﬁtted iteratively to the segmented points un-

der the assumption that independently moving objects

are of ﬁxed size and at different depths in the scene.

Segmented points are aligned with depth maps to

ascertain depths for moving object annotation. The

mode depth of these points is used to scale a bounding

box which is robustly ﬁt to the segmented points, such

that the number of inliers are maximised. To segment

more than one object, the bounding box algorithm is

reapplied to the ‘bounding box outliers’ produced in

the previous iteration. This needs to be done judi-

ciously, as these outliers may be misclassiﬁed back-

ground points that are distributed disparately in the

image. However, if a bimodal (or indeed multimodal)

distribution of foreground depths is present, objects

will be segmented in order of how numerously they

are annotated at a consistent depth. In the current real-

time implementation of the navigation system, bound-

ing boxes are only ﬁtted to the object which is most

numerously annotated at a consistent depth. This is,

almost without exception, the nearest object. Only

processing the nearest object simpliﬁes the sound map

provided to user, thus providing only the most rel-

evant information and making the audio feed easier

to interpret. For example, in a scene where there are

two objects present at different depths, the one with

the greater number of tracking points will be robustly

identiﬁed ﬁrst, assuming both sets of tracking points

demonstrate similar variance in their depth values.

2.1 Depth Estimation

In order to estimate the distance of objects from the

user in an efﬁcient manner, a stereo grid with two

GENERIC MOTION BASED OBJECT SEGMENTATION FOR ASSISTED NAVIGATION

451

cameras is used since it is generally faster than sin-

gle camera temporal depth estimation. The intrinsic

and extrinsic parameters of the two cameras are pre-

computed using a classic chart-based calibration tech-

nique (Zhang, 1998). Sparse depth estimation, e.g.

correlation based patch correspondence search and

reconstruction, is usually computationally efﬁcient.

However, it is not desirable in our application since

it often results in isolated regions even though they

may belong to a single object which makes it difﬁcult

to sonify. In recent years, there has been considerable

interest in dense depth estimation, e.g. (Scharstein

and Szeliski, 2002). We have experimented with sev-

eral methods, including belief propagation (Felzen-

szwalb and Huttenlocher, 2006), dynamic program-

ming (Birchﬁeld and Tomasi, 1999), sum of absolute

difference with winner-take-all optimisation (Kanade,

1994), and sum of squared differences with iterative

aggregation (Zitnick and Kanade, 2000).

Although recent comparative studies, such as

(Scharstein and Szeliski, 2002), suggest that scan

line based dynamic programming does not perform as

well as more global optimisation approaches, on our

outdoor dataset it appears to be a reasonable trade-

off between computational efﬁciency and quality (see

subjective comparison in Fig. 2 in the Results sec-

tion). Note that our outdoor images are considerably

different from those benchmarks widely used in com-

parative studies. It is very common for our data to

contain disparities of up to 60 pixels out of 320 pixels,

which is signiﬁcantly larger than most standard ones.

Additionally, the variation of disparities is large, i.e.

for most of the frames the disparity covers most lev-

els from 0 to 60. A typical dynamic programming

approach is the scanline-based 1D optimisation pro-

cess. We follow (Birchﬁeld and Tomasi, 1999) to de-

ﬁne the cost function to minimise while matching two

scanlines as:

γ = N

− N

∑

d(x

, y

), (1)

where N

and N

are the number of occlusions and

matches respectively, κ

and κ

are weightings for

occlusion penalty and match reward respectively, and

function d(.) measures the dissimilarity between two

pixels x

and y

. For this dissimilarity measure, one

that is insensitive to image sampling is used:

d(x

, y

) = min

d(x

, y

, I

d(y

, x

, I

)

, (2)

where

dis deﬁned as:

d(x

, y

, I

) = min

−

)≤y≤(y

−

)

) −

(y)|, (3)

where I

) and I

) are intensity values for x

the left scanline and y

in the right scanline respec-

tively, and

is the linearly interpolated function be-

tween the sample points of the right scanline. The

Figure 1: Fusion of depth map with image segmentation.

1st row: the original left image and graph cut based seg-

mentation using colour and raw depth information; 2nd

row: original depth estimation and result after anisotropic

smoothing based on segmentation.

matching is also subject to a set of constraints, such

as unique and ordering constraint which simpliﬁes dy-

namic programming, and ‘sided’ occlusion constraint

to handle untextured areas. For further details, the

reader is refered to (Birchﬁeld and Tomasi, 1999).

However, due to the nature of the 1D optimi-

sation, streaking artifacts inevitably result, as well

as temporal inconsistency, known as ﬂicking effects.

Since the stereo cameras are constantly moving and

the scene often contains moving and deforming ob-

jects, enforcing temporal consistency does not nec-

essarily improve results. A median ﬁlter across the

scan lines is used to reduce the spatial inconsistency.

More advanced approaches, such as (Bobick and In-

tille, 1999), can be used, however, at a computational

cost we can not afford. Others, such as (Gong and

Yang, 2007), require dedicated hardware solutions.

We also adopt a fusion approach using image seg-

mentation based on the assumption that depth dis-

continuity often collocates with discontinuity in re-

gional statistics. Similar ideas have been recently ex-

plored, e.g. (Zitnick and Kang, 2007). However,

we use a post-fusion approach instead of depth esti-

mation from over-segmentation

. Smoothing is per-

formed within each region to avoid smudging across

the region boundaries. An example result is shown

in Fig. 1. This segmentation is based on graph cuts

(Felzenszwalb and Huttenlocher, 2004), which offers

the potential of multimodal fusion of depth, colour

components and sparse optical ﬂow to obtain more

Image segmentation is also required as part of a sub-

system in our CASBliP project, not discussed in this paper,

for assistance to partially sighted users. Hence, the com-

putational overhead of fusing depth information and image

segmentation is affordable.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

452

coherent segmentation. We are currently also in-

vestigating Mean Shift segmentation (Comaniciu and

Meer, 2002) to determine if a faster throughput can be

achieved without compromising accuracy.

2.2 Deducing Background Motion

Model

To determine the motion of an object of interest, we

use a robust approach to ﬁrst determine which KLT

points correspond to the background region. Speciﬁ-

cally, homography is repeatedly used to parameterise

a provisional model based on the trajectory of a subset

of randomly selected points over a sliding temporal

window and the most likely model retained. Outliers

to the most likely model correspond to independently

moving object annotation.

The robust technique used here is MLESAC (Torr

and Zisserman, 2000) and is outlined in Algorithm 1.

This method attempts to determine the parameters of

the background’s motion model, using the smallest

possible subset of that data. Samples are drawn ran-

domly and used to generate a provisional model. The

most likely parameter vector, assuming the outliers

are randomly distributed, is retained. For each provi-

sional model, it is necessary to iteratively determine

the mixing parameter, γ, (expected proportion of in-

liers), which yields the highest likelihood. Our use of

MLESAC as opposed to RANSAC (random sample

consensus) (Fischler and Bolles, 1981) is more ex-

pensive, but avoids the need for a predeﬁned inlier

threshold when determining a consensus.

Algorithm 1 Robustly identifying dominant model.

represents the KLT points for the current frame

WinDiam represens the radius of the sliding temporal

window

represents the subset of X

, tracked successfully for

current temporal window

prov

represents the current model

best

represents the best model

N is the number of samples required for dominant model

to be selected with 0.95 probability

Identify X

for j ← 1..N do

Randomly select s samples, X

from X

Calculate M

prov

, using X

i−WinDiam

and X

Evaluate the likelihood, L

prov

, for M

prov

if L

prov

> L

best

then

best

← L

prov

best

← M

prov

Record outliers associated with M

best

end if

end for

Record M

best

and its’ associated outliers

With regard to model parametrization, the direct

linear transformation (DLT) may be used to calcu-

late a matrix, H, which transforms a set of points x

from one image to a set of corresponding points x

in another image. In order to fully constrain H, four

point correspondences are required (Hartley and Zis-

serman, 2001) (which are not collinear). If the four

points selected are background points, then the trans-

formation matrix deduced will describe the motion of

the background. The transformation

= Hx

, (4)

can also be expressed in the form:

× Hx

= 0, (5)

where × is the vector cross product. If the j-th

row of the matrix H is represented by h

and x

, y

, w

)

, this may be simpliﬁed to:

−w

−x

| {z }









= 0. (6)

Decomposing A, with SVD, produces the follow-

ing factorization:

A = UDV

. (7)

The columns of V, whose corresponding elements

in D are zero, form an orthonormal basis for the

nullspace of H (Press et al., 1992). In other words,

they provide a value for h, which satisﬁes Ah = 0.

2.3 Fitting a Bounding Box

We assume that the outliers to the background model

primarily represent the foreground object. The di-

mensions of the bounding box are determined by mul-

tiplying the foreground points’ mode depth by a scal-

ing factor which has been empirically determined. We

utilise the mode, as opposed to the mean, as it is more

robust to outliers and allows the possibility of isolat-

ing more than one object if the objects’ depths corre-

spond to a multimodal distribution.

The box is ﬁtted to the foreground points using

RANSAC as summarised in Algorithm 2. For every

frame, the object’s centroid is estimated using three

randomly selected foreground points. The bounding

box is then ﬁtted to the foreground points, based on

this estimation and the number of points lying within

the bounding box. It is appropriate to use RANSAC in

this case as the threshold is determined by the bound-

ing box size.

It would be possible to simply use a single fore-

ground point to estimate the object’s centroid, but us-

ing a greater number allows for more variety in the

GENERIC MOTION BASED OBJECT SEGMENTATION FOR ASSISTED NAVIGATION

453

Figure 2: 1st row: stereo images and depth estimation based on dynamic programming using 1D optimisation; 2nd row:

results obtained from belief propagation, sum of absolute differences with winner-take-all optimisation, and sum of squared

differences with iterative aggregation.

Algorithm 2 Robustly bounding ﬁtting.

out

represents the KLT points which are outliers to the

dominant model, M

best

CoG

prov

represents the current centroid for the bounding

box

CoG

best

represents the centroid yielding the greatest

number of inliers

N is the number of samples required for dominant model

to be selected with 0.95 probability

Calculate mode depth of X

out

Scale bounding box size proportionally to mode depth

and weighted average of centroid estimations for previ-

ous frames.

for j ← 1..N do

Select s random samples, X

out

from X

out

Calculate CoG

prov

: the centroid of X

out

Count the number of inliers ρ

prov

, for CoG

prov

if ρ

prov

> ρ

best

then

best

← ρ

prov

CoG

best

← ρ

prov

end if

end for

Use weighted average of CoG

best

and previous estima-

tions and record associated inliers

centroid’s position. However, using more points re-

quires more iterations in the RANSAC algorithm, so

3 are selected as a compromise. The bounding box’s

size and location tends to jitter due to the random

sampling and inconsistency with regard to features

annotated by the KLT tracker. Hence both quantities

are smoothed by utilising a weighted average of their

current and previous values.

In addition to ﬁtting a bounding box to the anno-

tation, aligning KLT points with depth maps can gen-

erate relative velocity estimates as motion in the im-

age plane may be scaled according to the moving ob-

jects distance to that plane. Furthermore, it could po-

tentially allow the system to determine if objects are

approaching the user. Alignment is relatively simple

since as the cameras are calibrated, the original im-

ages and the depth maps can be rectiﬁed and aligned

based on calibration parameters.

3 RESULTS

In Fig. 2 we illustrate a comparison of several depth

estimation techniques, e.g. belief propagation, sum

of absolute differences with winner-take-all optimi-

sation, and sum of squared differences with iterative

aggregation. We selected the method presented in

(Birchﬁeld and Tomasi, 1999) for reasonable accu-

racy as a trade-off for computational efﬁciency for

reasons as described in section 2.1.

Fig. 3 illustrates the annotation and bounding box

ﬁtting process. From left to right the images show:

the KLT points, the points segmented into domi-

nant motion (red) and outliers (blue), the depth map

aligned with these segmented points, with bounding

box ﬁtted and the right shows the ﬁnal annotation.

Note that the depth map is smaller as it only includes

portions of the scene captured by both cameras. This

process is also illustrated in Fig. 4. Note that depth

maps are produced concurrently with the sparse point

segmentation.

Figures 5, 6 and 7 are examples of the algorithm’s

output. In each ﬁgure every fourth frame is shown

starting top left and ﬁnishing bottom right. Pairs of

images represent each frame of the sequence with the

upper image illustrating the segmentation and depth

maps and the lower the ﬁnal annotation.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

454

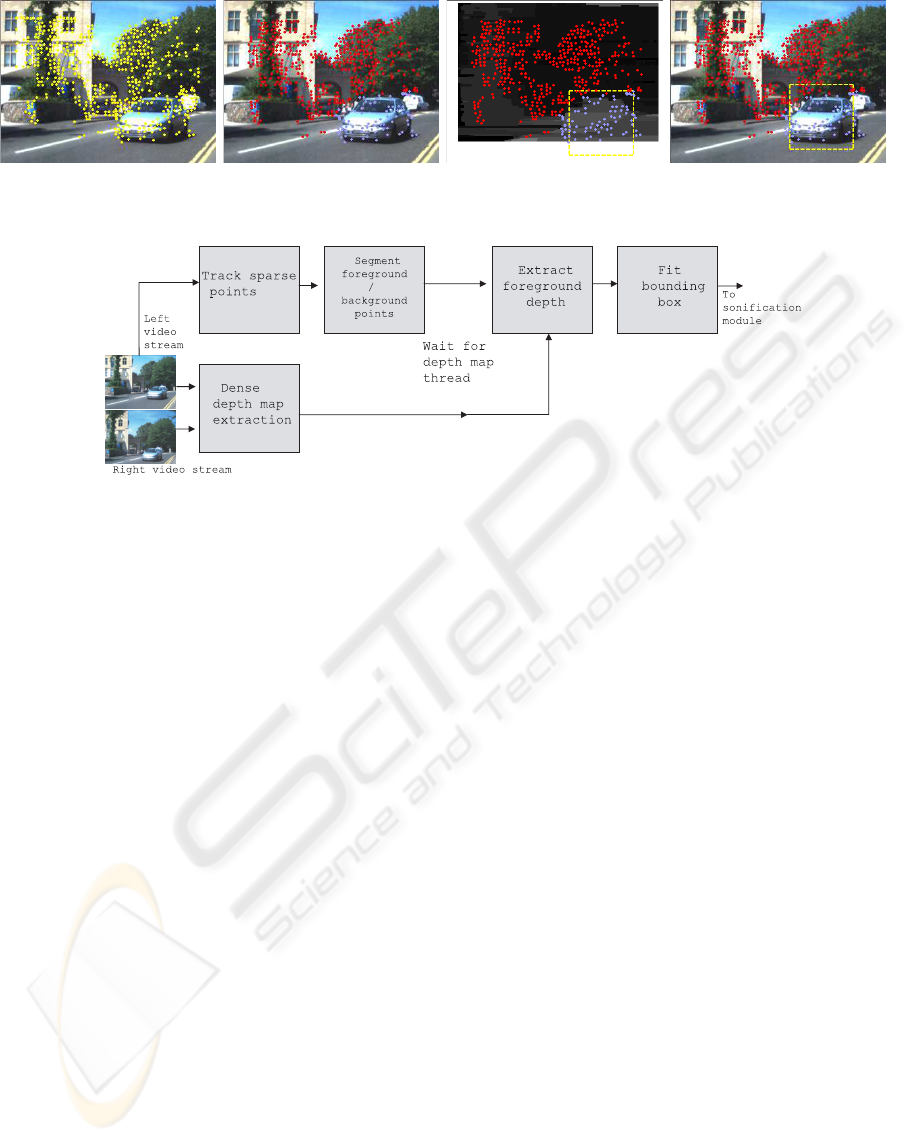
Figure 3: Left to right: sparse point tracking, foreground background segmentation and alignment with depth map, and ﬁnal

annotation.

Figure 4: Flow chart illustrating bounding box algorithm and relationship with depth map extraction.

4 DISCUSSION

The system currently runs at a rate of around 8fps

on a 2.39GHz laptop with 3GB RAM working on

320 × 240 images, when dealing with a single dom-

inant object only; hence further reﬁnement is neces-

sary to be able to handle multiple objects in real-time.

We have come across no previous works with sim-

ilar setups to ours, which deal with hazard detection in

the outdoors using wearable cameras for blind users,

to compare our results with. There are other works

with a similar application in mind, e.g.: (Andersen

and Seibel, 2001) in which a system is very brieﬂy

described for users with low vision, rather than no vi-

sion at all, thus relying on some user ability to see and

interpret the scene; and (Wilson et al., 2007) in which

a tactile-input wearable audio system is described.

Also, comparisons are not easy to establish as other

systems have proprietary software and hardware or

require signiﬁcant software redevelopment. There are

also advanced works on pedestrian detection or vehi-

cle detection, but these are mainly highly ﬁne-tuned

towards those speciﬁc classes of objects, whereas our

work is simply looking for any unspeciﬁed moving

objects in the scene to report audio warnings to blind

users. Furthermore, our system is designed to be lib-

eral in determining hazardous objects as it is impor-

tant to report a safe object as unsafe, than vice versa.

Hence, it is deemed reasonable for our bounding box

to be larger and a less accurate tight ﬁt.

5 CONCLUSIONS

A robust approach to annotating independently mov-

ing objects using head mounted stereo cameras has

been proposed. This is intended for use as part of an

audio-feedback system for reporting potentially haz-

ardous objects to a blind user navigating in outdoor

cityscape settings. Generic object detection is per-

formed, without any speciﬁc object classiﬁcation, to

ensure fast enough performance to allow practicality

of use. The system offers near real-time performance

and is robust enough to tolerate the unpredictable mo-

tions associated with head mounted stereo cameras.

Future work will focus on improving performance us-

ing accelerated feature tracking on the GPU.

ACKNOWLEDGEMENTS

This work was funded by EU-FP6 Project CASBliP

no. 027083 FP6-2004-IST-4.

REFERENCES

Andersen, J. and Seibel, E. (2001). Real-time hazard detec-

tion via machine vision for wearable low vision aids.

In ISWC ’01: Proceedings of the 5th IEEE Interna-

tional Symposium on Wearable Computers, page 182.

IEEE Computer Society.

GENERIC MOTION BASED OBJECT SEGMENTATION FOR ASSISTED NAVIGATION

455

Badino, H. (2004). A robust approach for ego-motion es-

timation using a mobile stereo platform. In 1st In-

ternation Workshop on Complex Motion (IWCM04),

volume 3417, pages 198–208.

Birchﬁeld, S. and Tomasi, C. (1999). Depth discontinu-

ities by pixel-to-pixel stereo. Int. J. Comput. Vision,

35(3):269–293.

Bobick, A. and Intille, S. (1999). Large occlusion stereo.

Int. J. Comput. Vision, 33(3):181–200.

Comaniciu, D. and Meer, P. (2002). Mean shift: a robust

approach toward feature space analysis. IEEE Trans.

PAMI, 24(5):603–619.

de Souza, G. and Kak, A. (2002). Vision for mobile robot

navigation: A survey. 24(2):237–267.

Ess, A., Leibe, B., and van Gool, L. (2007). Depth and ap-

pearance for mobile scene analysis. In ICCV07, pages

1–8.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2004). Efﬁcient

graph-based image segmentation. Int. J. Comput. Vi-

sion, 59(2):167–181.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2006). Efﬁcient

belief propagation for early vision. Int. J. Comput.

Vision, 70(1):41–54.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Commun. ACM, 24(6):381–395.

Gong, M. and Yang, Y. (2007). Real-time stereo matching

using orthogonal reliability-based dynamic program-

ming. IEEE Trans. Image Processing, 16(3):879–884.

Hannuna, S. (2007). Quadruped Gait Detection in Low

Quality Wildlife Video. PhD thesis, University of Bris-

tol. Supervisor-Neill Campbell.

Hartley, R. I. and Zisserman, A. (2001). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521623049.

Kanade, T. (1994). Development of a video-rate stereo ma-

chine. In Image Understanding Workshop, pages 549–

9557.

Leonard, J. (2007). Challenges for autonomous mobile

robots. pages 4–4.

Pauwels, K. and Hulle, M. M. V. (2004). Segmenting inde-

pendently moving objects from egomotion ﬂow ﬁelds.

In Proc. Early Cognitive Vision Workshop.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-

nery, B. P. (1992). Numerical Recipes in C: The Art

of Scientiﬁc Computing. Cambridge University Press,

New York, NY, USA.

Rabe, C., Franke, U., and Gehrig, S. (2007). Fast detection

of moving objects in complex scenarios. Intelligent

Vehicles Symposium, 2007 IEEE., pages 398–403.

Scharstein, D. and Szeliski, R. (2002). A taxonomy and

evaluation of dense two-frame stereo correspondence

algorithms. Int. J. Comput. Vision, 47(1-3):7–42.

Shi, J. and Tomasi, C. (1994). Good features to track.

In IEEE Conference on Computer Vision and Pattern

Recognition (CVPR’94), Seattle.

Torr, P. and Zisserman, A. (2000). Mlesac: A new ro-

bust estimator with application to estimating image

geometry. Computer Vision and Image Understand-

ing, 78:138–156.

Veksler, O. (2003). Extracting dense features for visual cor-

respondence with graph cuts. In IEEE CVPR, pages –.

Wilson, J., Walker, B., Lindsay, J., and Dellaert, F. (2007).

Swan: System for wearable audio navigation.

Yang, Q., Wang, L., Yang, R., Wang, S., Liao, M., and Nis-

ter, D. (2006). Real-time global stereo matching using

hierarchical belief propagation. In BMVC, pages –.

Yu, Q., Ara

ujo, H., and Wang, H. (2005). A stereovision

method for obstacle detection and tracking in non-ﬂat

urban environments. Auton. Robots, 19(2):141–157.

Yuan, C., Medioni, G. G., Kang, J., and Cohen, I. (2007).

Detecting motion regions in the presence of a strong

parallax from a moving camera by multiview geomet-

ric constraints. IEEE Trans. Pattern Anal. Mach. In-

tell., 29(9):1627–1641.

Zhang, Z. (1998). Determining the epipolar geometry and

its uncertainty: A review. Int. J. Comput. Vision,

27(2):161–195.

Zitnick, C. and Kanade, T. (2000). A cooperative algorithm

for stereo matching and occlusion detection. IEEE

Trans. PAMI, 22(7):675–684.

Zitnick, C. and Kang, S. (2007). Stereo for image-based

rendering using image over-segmentation. Int. J.

Comput. Vision, 75:49–65.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

456

Figure 5: Every fourth frame of car approaching the cameras (depth maps and original frames are paired vertically).

Figure 6: Every fourth frame of cyclist moving away from the cameras (depth maps and original frames are paired vertically).

Figure 7: Every fourth frame of a person walking in the same direction as camera egomotion (depth maps and original frames

are paired vertically).

GENERIC MOTION BASED OBJECT SEGMENTATION FOR ASSISTED NAVIGATION

457