EXPERIMENTAL COMPARISON OF WIDE BASELINE

CORRESPONDENCE ALGORITHMS FOR MULTI CAMERA

CALIBRATION

Ferid Bajramovic, Michael Koch and Joachim Denzler

Chair for Computer Vision, Friedrich Schiller University of Jena, Ernst-Abbe-Platz 2, 07743 Jena, Germany

Keywords:

Correspondence, Calibration, Structure-from-motion, Uncertainty.

Abstract:

The quality of point correspondences is crucial for the successful application of multi camera self-calibration

procedures. There are several interest point detectors, local descriptors and matching algorithms, which can

be combined almost arbitrarily. In this paper, we compare the point correspondences produced by several such

combinations. In contrast to previous comparisons, we evaluate the correspondences based on the accuracy of

relative pose estimation and multi camera calibration.

1 INTRODUCTION

Calibration is an important prerequisite for many ap-

plications of multi camera systems. The most conve-

nient, but also the most challenging class of calibra-

tion methods uses only images from the cameras as

input—without any scene knowledge or user interac-

tion (Martinec and Pajdla, 2007; Verg´es-Llah´ı et al.,

2008; Bajramovic and Denzler, 2008). The success

of such methods crucially depends on the point cor-

respondences which are extracted from the images in

the ﬁrst step.

Correspondence extraction typically consists of

three steps: detection of points (or regions) of interest,

computation of a local descriptor for each point, and

matching of the descriptors. In this paper, we exper-

imentally compare several alternative algorithms for

all three steps. Unlike other comparisons (Mikola-

jczyk et al., 2005; Mikolajczyk and Schmid, 2005),

we evaluate, how well the various correspondence

methods are suited for relative pose estimation and

multi camera calibration.

The paper is structured as follows. In Section 2,

we brieﬂy describe the detectors, descriptors and

matching algorithms. Section 3 continues with the

geometry estimation. In section 4, we present our ex-

perimental comparison. Conclusions are given in sec-

tion 5.

2 CORRESPONDENCES

In this section, we describe the methods which extract

pairwise point correspondences from images. A point

correspondence is a pair of 2D image points in two

diﬀerent images which represent the same 3D scene

point. There is a general scheme for extracting point

correspondences. The ﬁrst step detects interest points

in each image. They should be invariant against dif-

ferent 3D world transformations and changes in il-

lumination, such that they can be found in diﬀerent

views of the same scene. Afterwards, a descriptor

is calculated for every interest point which usually

stores information of the surrounding area of the 2D

image point. The last step consists of matching the

descriptors in order to establish correspondences be-

tween 2D points in diﬀerent images.

2.1 Detectors

The detection of interest points is a wide-spread ﬁeld.

In recent years, many diﬀerent kinds of detectors have

been developed. The most important attribute is the

afore mentioned invariance. Most of the detectors are

invariant against rotation, translation and scale. We

base our selection on the work of Mikolajczyk et al.

(Mikolajczyk et al., 2005; Mikolajczyk and Schmid,

2005).

458

Bajramovic F., Koch M. and Denzler J. (2009).

EXPERIMENTAL COMPARISON OF WIDE BASELINE CORRESPONDENCE ALGORITHMS FOR MULTI CAMERA CALIBRATION.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 458-463

DOI: 10.5220/0001786004580463

 SciTePress

2.1.1 Harris-Laplace

The Harris-Laplace (HarLap) detector (Mikolajczyk

and Schmid, 2002) is based on the Harris-Stephens

corner detector (Harris and Stephens, 1988). In addi-

tion, it uses a Gaussian scale space to achieve scale in-

variance. Hence, the second moment matrix becomes:

S = σ

· g(σ

)∗

(x, σ

) I

(x, σ

)

(x, σ

) I

(x, σ

)

. (1)

The variable σ

indicates the scale space kernel and

designates the Gaussian smoothing kernel of the

Gaussian function g. I

(x, σ

) and I

(x, σ

) deﬁne

the smoothed derivatives in the corresponding image

directions. The Harris-Stephens corner detector is ap-

plied to diﬀerent scales and a speciﬁc scale is chosen

by an iterative algorithm (Lindeberg, 1998). After-

wards, the interest points are selected according to the

“cornerness” c = det(S)− α · trace

(S). The constant α

is usually set to 0.04.

2.1.2 Hessian-Laplace

For the Hessian-Laplace (HesLap) detector (Mikola-

jczyk et al., 2005) the second moment matrix is re-

placed by the Hessian. Points which are local extrema

of both, the determinant and the trace of the Hessian,

are selected as interest points.

2.1.3 Aﬃne Regions

The aﬃ ne region detectors (HarAﬀ, HesAﬀ) extend

the Harris-Laplace and Hessian-Laplace detectors

by an iterative algorithm (Mikolajczyk and Schmid,

2002) which computes the second-moment matrix or

the Hessian matrix, respectively, which transforms the

anisotropic region into a normalized region.

2.1.4 Diﬀerence of Gaussian

The diﬀerence of Gaussian (DOG) detector described

by Lowe (Lowe, 2004) uses a diﬀerence of Gaussian

scale space to detect interest points. The main aspect

is the scale invariance of the keypoints. The problem

of the strong response to edges is solved by using the

Harris-Stephens detector (Harris and Stephens, 1988)

to suppress unstable keypoints along edges.

2.1.5 Intensity based Regions

The intensity based regions (IBR) detector (Tuyte-

laars and van Gool, 2000) uses only the image in-

tensity information. First, local extrema in the image

are detected using non-maximum suppression. After-

wards, the developing of the intensity values on rays

with diﬀerent angles starting from the extremum is

analyzed. On each ray, one local extremum of a spe-

cial intensity function is computed. Those are used to

ﬁt an ellipse to get a region which is invariant against

aﬃne transformations and additive illumination.

2.2 Descriptors

Next, we will introduce the descriptors used in our

comparison. As mentioned before, they attempt to

describe the interest points as invariantly as possible

based on the image information.

2.2.1 SIFT

The scale invariant feature transform (SIFT) descrip-

tor was ﬁrst described by Lowe (Lowe, 2004). It gen-

erates a special gradient histogram as a vector of 128

entries from the area around the interest point.

2.2.2 Gradient Location and Orientation

Histogram

Gradient Location and Orientation Histogram

(GLOH) (Mikolajczyk and Schmid, 2005) is an

extension of SIFT. It computes the SIFT descriptor

on a log-polar location grid with diﬀerent radial

and angular directions in a total of 17 parameters

for location. Gradient orientations are quantized to

16 values. The dimension of the resulting vector is

reduced from 272 to 128 by principal component

analysis (PCA).

2.2.3 Steerable Filters

Steerable ﬁlters (JLA) use derivatives computed by

convolution with Gaussian derivatives using σ = 6.7

(Freeman and Adelson, 1991) for an image patch.

The derivatives are calculated up to fourth order and

the resulting descriptor has dimension 14.

2.2.4 Moments

Moment invariants (MOM) (van Gool et al., 1996) de-

scribe the intensity and shape distribution information

surrounding a keypoint (image region Ω). They are

deﬁned by M

R R

Ω

(

(u, v)

)

dudv with order

p+ q and degree a using image gradients I

in x and y

direction (d ∈ {x, y}). The invariant moments are com-

puted up to second order and second degree. Hence,

the resulting descriptor has dimension 20.

EXPERIMENTAL COMPARISON OF WIDE BASELINE CORRESPONDENCE ALGORITHMS FOR MULTI

CAMERA CALIBRATION

459

2.3 Matching

After computing the sets of descriptors A and B for

all interest points in two images, we compute corre-

spondences as a subset of C = A × B. We limit the

number of correspondences to 100 in each image pair.

2.3.1 Exhaustive Search

The exhaustive search (ES) matching builds a matrix

D which consists of the distance measures between

the descriptors for each element of C with

D = (d

), d

= dist(a

, b

), a

∈ A and b

∈ B. (2)

Normally, the distance measure dist is Euclidean.

Point correspondences are selected by choosing the

k interest points with minimum descriptor distances

incrementally according to the uniqueness constraint.

2.3.2 Nearest Neighbor Matching

In the ﬁrst step of nearest neighbor (NN) matching, a

set of correspondence candidates is constructed. Each

element of the descriptor set B is assigned to the near-

est neighbor in A. The second step is identical to

exhaustive search. From the intial set, the best k cor-

respondencesare selected incrementally enforcing the

uniqueness constraint. The main diﬀerence to exhaus-

tive search can be interpreted as considering only part

of the matrix D for the ﬁnal selection.

2.3.3 Two Nearest Neighbor Matching

Two nearest neighbor (2NN) is an extension of near-

est neighbor matching described by (Lowe, 2004)

aimed at removing ambiguous matchings. When

matching a given descriptor in B to its nearest neigh-

bor in A, we also compute the distance to the second

nearest neighbor. A candidate match is only estab-

lished if the ratio of the two distances is below a cer-

tain threshold (typically 0.8).

2.3.4 K-Hungarian Matching

The Hungarian (Hun) method is used for “minimum

weight” bipartite graph matching. It is also applica-

ble for matching point correspondences as shown by

Keysers et al. (Keysers et al., 2004). In this context,

the interest points in two images become the vertices

of the complete bipartite graph. The edge weights are

given by the distance between the descriptors of the

two points. The Hungarian matching computes the

optimal solution in the sense of least summed descrip-

tor distance of all point correspondences.

The problem of this method are the high com-

putational costs of O(m

) with m = |A| and n =

|B|. Hence, we propose the following approxima-

tion which consists of reducing the number of interest

points and thus vertices in the bipartite graph. We ﬁrst

calculate l < min(m, n) initial correspondences

C ⊆ C

using another method that needs less time than the

Hungarian method. In the experiments, we use ex-

haustive search.

The set

C induces a subset of l interest points in

each image:

A ⊆ A and

B ⊆ B. The subset

of in-

terest points in the ﬁrst image used for the Hungarian

method is computed incrementally as follows: begin

with

A and for each point p ∈

B, add the k nearest

neighbors within A \

. The subset

is deﬁned

accordingly. The number of vertices in the result-

ing complete bipartite graph is at most 2l(k + 1). Ap-

plying the Hungarian method to it produces at most

l(k+ 1) correspondences. The exact number of corre-

spondences can vary greatly.

The total runtime of our approximate Hungarian

matching consists of the initial extraction of l corre-

spondences, building the reduced bipartite graph and

applying the Hungarian method. The complexity of

the last step will typically dominate the whole algo-

rithm and is O((l· (k+ 1))

3 CALIBRATION

Given a set of cameras with known intrinsic param-

eters, we want to estimate the extrinsic parameters

up to a similarity transformation. We use our pro-

cedure described in (Bajramovic and Denzler, 2008).

We ﬁrst estimate pairwise relative poses, which are

subsequently composed to absolute poses. We will

brieﬂy describe both steps in this section. For details,

the reader is referred to the afore mentioned paper.

3.1 Relative Pose Estimation

We use the ﬁve point algorithm (Stew´enius et al.,

2006; Br¨uckner et al., 2008) to estimate relative poses

(up to scale) between camera pairs with suﬃciently

many point correspondences and known intrinsic pa-

rameters. As the point correspondences must be ex-

pected to contain false matches (outliers), we embed

the ﬁve point algorithm into a robust sampling al-

gorithm (Bajramovic and Denzler, 2008; Engels and

Nist´er, 2005) similar to the RANSAC (Fischler and

Bolles, 1981) variant MLESAC (Torr and Zisserman,

2000). There are two diﬀerences to RANSAC:

1. Instead of computing a support set, a probabil-

ity density function p(R, t | D) is evaluated for

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

460

each hypothesis (R, t) with regard to all corre-

spondences D. I.e. the sampling process approxi-

mates argmax

R,t

p(R, t | D). Outliers are incorpo-

rated by using the Blake-Zisserman distribution.

2. A discrete approximation to p(t | D) is built dur-

ing the iteration. Its entropy is used as an un-

certainty measure w(

t) for the resulting relative

pose estimate (

t).

3.2 Multi Camera Calibration

We (Bajramovic and Denzler, 2008) compose relative

poses to absolute ones by ﬁrst estimating the unknown

scale factors in the estimated relative poses (up to a

common unknown scale factor) and then concatenat-

ing the later. The procedure can be formalized by us-

ing the camera dependency graph which consists of a

vertex for each camera and an edge for each known

relative pose. We use triangulation to estimate the

scale factors and hence have to work on triangles in

the graph. As triangulation only eliminates two out

of three unknown scale factors, we arbitrarily choose

one of the scale factors in the ﬁrst triangle and subse-

quently propagate scale factors from triangle to trian-

gle. Moving from triangle to triangle can be expressed

as traversing an auxiliary graph which represents the

triangles as vertices.

As only a subset of relative poses is actually re-

quired for that process, the traversal order implies a

selection of relative poses. We use the uncertainty

measures computed during relative pose estimation to

guide that selection. The main idea consists of inter-

preting the uncertainties as edge weights in the cam-

era dependency graph and calibrating along a set of

shortest triangle paths. Algorithmically, such paths

are computed by applying Dijkstra to an extension

of the triangle graph. Using shortest triangle paths

is equivalent to selecting the subset of relative poses

with minimum total uncertainty.

4 EXPERIMENTS

We use two diﬀerent experimental setups. The ﬁrst

one consists of two AVT Marlin monochrome cam-

eras and six AVT Pike color cameras observing a

scene, as depicted in Figure 1. We estimate the intrin-

sic camera parameters using Zhang’s (Zhang, 2000)

calibration pattern based method. To be able to eval-

uate our calibration results, we use Zhang’s method

also to compute a “ground truth” for the extrinsic cal-

ibration. Note that this “ground truth” is not free of

errors, but still provides a reasonable comparison. For

the second experiment, we use a robot arm to move a

Sony DFW-VL500 camera to 15 diﬀerent poses. The

arm provides us with reliable ground truth poses.

We use the detectors and descriptors implementa-

tion of Mikolajczyk et al. (Mikolajczyk et al., 2005;

Mikolajczyk and Schmid, 2005) except for IBR. For

the DOG-SIFT combination, we alternatively also use

the SIFT++ implementation (Vedaldi, 2007).

4.1 Error Measures

In order to measure the accuracy of relative pose es-

timates, we compare the estimated translation vector

to the ground truth. As the scale and sign are un-

determined, we use the angle in degree between the

two vectors ignoring direction, i.e. the error is at most

◦

. Each experiment is repeated 10 times, as the re-

sults depend on random sampling. The accuracy of

relative pose estimates is evaluated using all images

pairs and all repetitions.

In order to evaluate a multi camera calibration, it

ﬁrst has to be registered with the ground truth to com-

pensate for the undetermined similarity transforma-

tion. We use a randomized least median of squares

estimator based on a nonlinear registration algorithm

with linear initialization. We take the median distance

between calibrated and ground truth camera positions

as error measure for the multi camera calibration. The

scale of the error measure is determined by the scale

of the ground truth, which is normalized such that the

ﬁrst two cameras have distance 100.

4.2 Results

First, we analyze the matching algorithms and then

compare detectors and descriptors using only the best

matching method. Figures 2 and 3 show the errors on

the relative pose estimates and the multi camera cali-

bration. The results are aggregated over all detectors

and descriptors in a boxplot (Tukey, 1977). A boxplot

contains a box depicting the 0.25 and 0.75 quantiles.

The line in the box is the median. The bars indicate

the remaining spread. Crosses are outliers.

Two nearest neighbor (2NN) gives the best results,

closely followed by nearest neighbor (NN). The high

error outliers of 2NN can be explained by the fact that

it produces no correspondences when applied to the

IBR detector. Exhaustive search (ES) shows similar

performance in the multi camera experiment, but is

considerably worse on the robot arm data. The results

for K-Hungarian (Hun) matching are quite poor.

Figures 4 and 5 show the relative pose errors

and the multi camera calibration errors, respectively,

using 2NN matching for all detector and descriptor

combinations – except for IBR, which uses NN. The

EXPERIMENTAL COMPARISON OF WIDE BASELINE CORRESPONDENCE ALGORITHMS FOR MULTI

CAMERA CALIBRATION

461

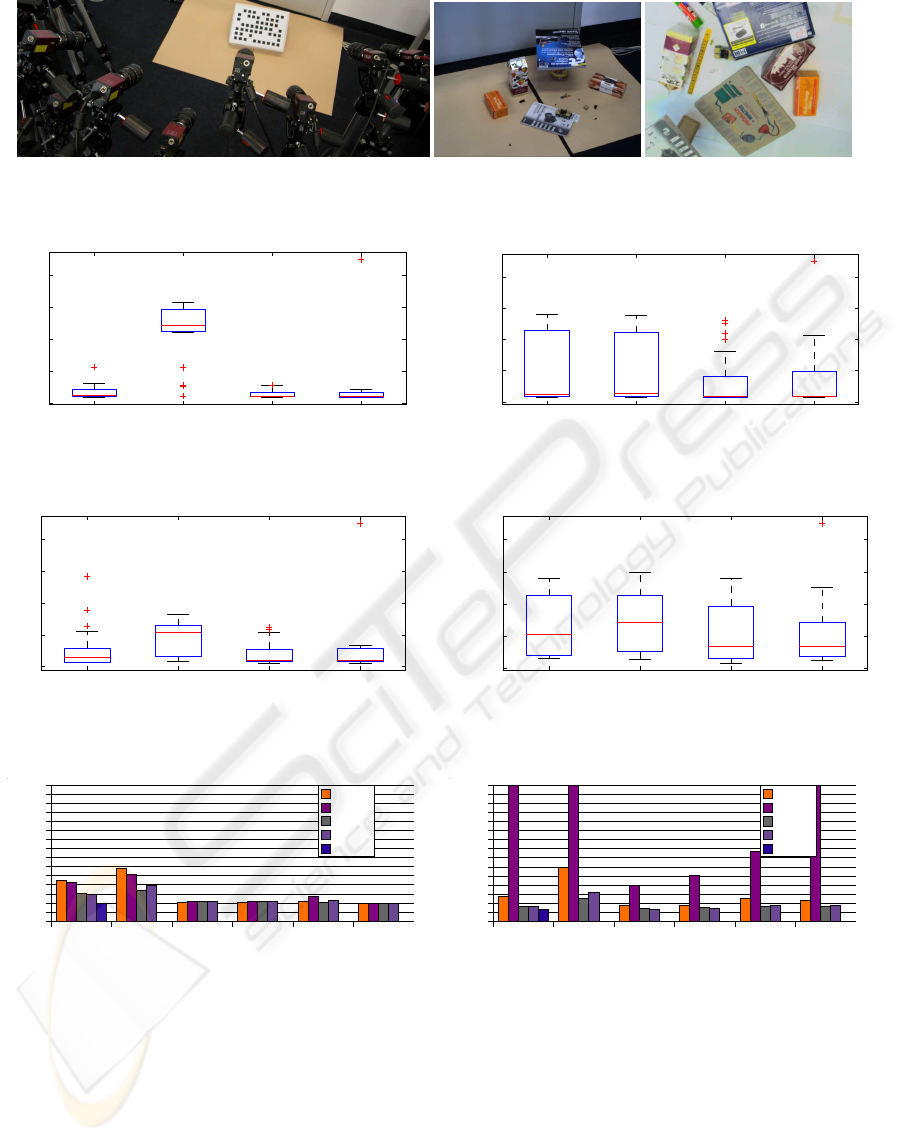
Figure 1: Experimental setups. Left: the multi camera system used in the ﬁrst experiment observing the pattern for the Zhang

calibration, middle: the according scene (image from the sixth camera), right: the scene used in the robot arm experiment.

translation error in degree

Hun NN 2NN

translation error in degree

Hun NN 2NN

Figure 2: Relative poses: median of translation errors in degrees as a boxplot (Tukey, 1977), which is described brieﬂy in the

text. Left: multi camera system, right: robot arm.

median position error in percent

Hun

2NN

median position error in percent

Hun

2NN

Figure 3: Multi camera calibration: median of median camera position errors in percent as a boxplot (Tukey, 1977), which is

described brieﬂy in the text. Left: multi camera system, right: robot arm.

     



























 ! !!"#

     



























 ! !!"#

Figure 4: Relative poses: median of translation errors in degrees (truncated at 30) for all detectors and descriptors using

nearest neighbor matching. Left: multi camera system, right: robot arm.

Harris and Hessian detectors show the best overall

performance. The inﬂuence of the aﬃne region exten-

sion varies. The comparatively bad results of the dif-

ference of Gaussian (DOG) detector might be imple-

mentation and parameter speciﬁc. The SIFT++ im-

plementation shows much better results. IBR is gen-

erally not very reliable. As for the descriptor, SIFT

and GLOH give the best results with no clear winner.

Steerable ﬁlters (JLA) and invariant moments (MOM)

can give similarly good results as SIFT and GLOH in

some situations, but seem to be less robust.

5 CONCLUSIONS

We performed an experimental comparison of several

interest point detectors, local descriptors and match-

ing algorithms in the context of relative pose estima-

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

462

     



























 !"! !  #"

     



























 !"! !  #"

Figure 5: Multi camera calibration: median of median camera position errors in percent (truncated at 30) for all detectors and

descriptors using nearest neighbor matching. Left: multi camera system, right: robot arm.

tion and multi camera calibration. The results con-

ﬁrmed the good performance of the SIFT descriptor.

Combined with the Harris/Hessian detectors, steer-

able ﬁlters and moment invariants could reach similar

results, but were less reliable. The GLOH extension

of SIFT did not show a pronounced improvement.

The performance of the DOG detector depended on

the implementation. The results of the SIFT++ ver-

sion were close to the Harris/Hessian detectors, which

gave the best results. As matching algorithm, two

nearest neighbor was the best choice.

REFERENCES

Bajramovic, F. and Denzler, J. (2008). Global Uncertainty-

based Selection of Relative Poses for Multi Camera

Calibration. In Proceedings of the British Machine Vi-

sion Conference (BMVC), volume 2, pages 745–754.

Br¨uckner, M., Bajramovic, F., and Denzler, J. (2008). Ex-

perimental Evaluation of Relative Pose Estimation Al-

gorithms. In Proc. of the Third International Conf. on

Computer Vision Theory and Applications (VISAPP),

volume 2, pages 431–438.

Engels, C. and Nist´er, D. (2005). Global uncertainty

in epipolar geometry via fully and partially data-

driven sampling. In ISPRS Workshop BenCOS: To-

wards Benchmarking Automated Calibration, Orien-

tation and Surface Reconstruction from Images, pages

17–22.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM, 24(6):381–395.

Freeman, W. T. and Adelson, E. H. (1991). The design and

use of steerable ﬁlters. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 13(9):891–906.

Harris, C. and Stephens, M. J. (1988). A combined corner

and edge detector. In Proceedings of The Fourth Alvey

Vision Conference, pages 147–151.

Keysers, D., Deselaers, T., and Ney, H. (2004). Pixel-to-

pixel matching for image recognition using hungarian

graph matching. In Proceedings of the DAGM Sympo-

sium on Pattern Recognition, pages 154–162.

Lindeberg, T. (1998). Feature detection with automatic

scale selection. International Journal of Computer Vi-

sion, 30(2):79–116.

Lowe, D. G. (2004). Distinctive Image Features from Scale-

Invariant Keypoints. International Journal of Com-

puter Vision (IJCV), 60(2):91–110.

Martinec, D. and Pajdla, T. (2007). Robust Rotation and

Translation Estimation in Multiview Reconstruction.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition (CVPR), pages 1–8.

Mikolajczyk, K. and Schmid, C. (2002). An aﬃne invari-

ant interest point detector. In Proceedings of the Eu-

ropean Conference on Computer Vision, volume 1,

pages 128–142.

Mikolajczyk, K. and Schmid, C. (2005). A perfor-

mance evaluation of local descriptors. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

27(10):1615–1630.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaﬀalitzky, F., Kadir, T., and van Gool,

L. (2005). A comparison of aﬃne region detectors.

International J. of Computer Vision, 65(7):43–72.

Stew´enius, H., Engels, C., and Nist´er, D. (2006). Re-

cent Developments on Direct Relative Orientation. IS-

PRS Journal of Photogrammetry and Remote Sensing,

60(4):284–294.

Torr, P. and Zisserman, A. (2000). MLESAC: A New Ro-

bust Estimator with Application to Estimating Image

Geometry. Computer Vision and Image Understand-

ing, 78(19):138–156.

Tukey, J. W. (1977). Exploratory Data Analysis. Addison-

Wesley, Reading, MA.

Tuytelaars, T. and van Gool, L. J. (2000). Wide Baseline

Stereo Matching based on Local, Aﬃnely Invariant

Regions. In Proceedings of the British Machine Vi-

sion Conference (BMVC), pages 412–425.

van Gool, L. J., Moons, T., and Ungureanu, D. (1996).

Aﬃne/photometric invariants for planar intensity pat-

terns. In Proceedings of the European Conference on

Computer Vision, volume 1, pages 642–651.

Vedaldi, A. (2007). An open implementation of the SIFT

detector and descriptor. Technical Report 070012,

UCLA CSD.

Verg´es-Llah´ı, J., Moldovan, D., and Wada, T. (2008). A

new reliability measure for essential matrices suitable

in multiple view calibration. In Proc. of the Third Int.

Conf. on Comp. Vision Theory and Applications (VIS-

APP), volume 1, pages 114–121.

Zhang, Z. (2000). A Flexible New Technique for Camera

Calibration. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 22(11):1330–1334.

EXPERIMENTAL COMPARISON OF WIDE BASELINE CORRESPONDENCE ALGORITHMS FOR MULTI

CAMERA CALIBRATION

463