MOTION-BASED FEATURE CLUSTERING FOR ARTICULATED

BODY TRACKING

Hildegard Kuehne and Annika Woerner

Institute for Algorithms and Cognitive Systems, University Karlsruhe(TH), Kaiserstr. 12, 76131 Karlsruhe, Germany

Keywords: Feature clustering, Motion principles, Articulated body tracking, Body structure reconstruction, Feature

tracking, Motion analysis.

Abstract: The recovery of three dimensional structures from moving elements is one of the main abilities of the

human perception system. It is mainly based on particularities of how we interpret moving features,

especially on the enforcement of geometrical grouping and definition of relation between features. In this

paper we evaluate how the human abilities of motion based feature clustering can be transferred to an

algorithmic approach to determine the structure of a rigid or articulated body in an image sequence. It shows

how to group sparse 3D motion features to structural clusters, describing the rigid elements of articulated

body structures. The location and motion properties of sparse feature point clouds have been analyzed and it

is shown that moving features can be clustered by their local and temporal properties without any additional

image information. The assembly of these structural groups could allow the detection of a human body in an

image as well as its pose estimation. So, such a clustering can establish a basis for a markerless

reconstruction of articulated body structures as well as for human motion recognition by moving features.

1 INTRODUCTION

One of the main abilities of the human perception

system is the interpretation of structure from motion.

It is possible for us to estimate the form and the

underlying body-structure of any object by only few

moving elements like lines and points. Additionally,

this ability is mostly independent from any

environmental influences like e.g. a moving

background, but also from the visual representation

of the object itself as e.g. its size, colour or surface

appearance.

This ability of motion perception is mainly based

on particularities of how we perceive and interpret

moving features, as has been shown in the

experiments with moving light displays of

Johansson (Johansson, 1973). The human perception

usually forces a geometrical grouping and definition

of relation between features. This can be based on

spatial relations who are partly defined and

summarized under the gestalt-principles, but also on

the analysis of motion properties. The alignment and

grouping of features allows the reconstruction of

complex structures and their recognition even under

not-optimal circumstances and with incomplete

visual information.

In this paper we present three different feature

clustering methods for 3D space and evaluate them

with respect to their applicability for articulated

body tracking. It is assumed, that every motion, and

so also the motion of a human body in an image will

result in some moving feature points. The motion of

these feature points can allow determining the

structure of the underlying rigid or articulated body.

One main step towards such an application

comprised the correct clustering of the moving

features in order to detected rigid moving elements

in the image. The presented approaches will show

how to group motion features to structural clusters,

describing the rigid elements of articulated body

structures.

For the practical realization, we captured several

image sequences with human motion. A motion

based feature tracking method is applied to extract

the moving features and to reconstruct their 3D

positions. The 3D positions and motion properties of

the resulting feature points are analysed in order to

find structural clusters. These structural clusters

describe feature sets with position and motion

properties, characteristically for moving rigid

structures, so that these clusters can be considered as

579

Kuehne H. and Woerner A. (2009).

MOTION-BASED FEATURE CLUSTERING FOR ARTICULATED BODY TRACKING.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 579-584

DOI: 10.5220/0001786105790584

 SciTePress

candidates for the determination and tracking of

underlying rigid body elements.

The assembly of these structural clusters could

allow the detection of a human body in an image as

well as its pose estimation and, considering a longer

observation period, even motion recognition. So

such a clustering can establish a basis for a

markerless reconstruction of articulated body

structures as well as for human motion recognition

by moving features.

2 STATE OF THE ART

Automatic detection and tracking of people in

different contexts has become a more and more

relevant area in computer vision, especially in the

context of motion analysis and recognition. The

growing importance of this field is shown by the

increasing number of surveys dealing with this

subject (Moeslund, 2001 and 2006; Aggarval, 1999).

Feature-based human motion detection and

analysis in this context is mainly based on marker

tracking as presented by Cedras et al. or Holstein et

al. (Cedras, 1994; Holstein, 2002), because

predefined marker positions usually allow direct

reconstruction of the underlying skeleton as shown

by Silaghi et al. (Silaghi, 1998). A first approach for

an application of markerless feature-based

techniques in the context of human motion

recognition is described by Song et al. (Song, 1999

and 2003). Here the motion of image features is used

to detect human motion in an image sequence and to

distinguish it from other moving elements, but the

overall motion is not analysed

The second thematic focused in the here

presented approach, the computation of feature

grouping based on motion primitives, has been first

described by Ullman (Ullman, 1983) and later by

Aggarval et al. (Aggarval, 1994). Here, the

applications range from basic computational studies

of about interpretation of structure and motion up to

optical flow based image segmentation (Nicolescu,

2002). We can see that, especially in the area of

optical flow segmentation most techniques are

designed for dense motion fields and so would

probably not work for sparse feature maps with

small structures, overlapping and twists, as they

occur in articulated body tracking.

But the perception of moving structures based on

the interpretation of motion is also still an open

problem in neuroscience (Giese, 2003).

3 THEORETICAL APPROACH

In order to group moving features to structural

clusters, it is first necessary to find acceptable

criteria, describing the location and motion

properties of points on rigid elements. The selection

of clustering criteria is mainly based on three

different approaches. The first two criteria are based

on human interpretation of perception of rigid

objects from 2-D motion presented e.g. by Ullman

(Ullman, 1983): The first one is the velocity-based

interpretation, where it is assumed that features that

move in the same direction belong to one object.

The second is the location-based interpretation,

which means, that features that lay close together

have a higher probability to belong to one object

than features that are far away from each other.

In the here presented approach these criteria are

extended to the three dimensional space. The

transfer of the location- and velocity-based criterion

from 2D to 3D is straight forward. And additionally

for 3D space, a third, distance-variation-based

criterion can be added. Assumed, that the features

are fixed on the underlying element and do not

change their 3D position relative to each other, they

will also preserve the distance to all features that are

lying on the same element. So, features whose

distance relative to each other does not change over

time are also probably suitable candidates to

determine a rigid object.

Assuming features are situated on one rigid

element, they will probably follow one or more of

follow criteria:

Location Criterion. Two feature points, a and b, are

rather located on the same rigid element if their 3D

mean distance d(a, b) over n frames, shown in

equation 1, is small:





,













,,



.,









(1)

Velocity Criterion. If two feature points, a and b,

have the same or a similar motion vector v(a) at the

same time i, as described in equation 2, they are also

likely to be located on the same rigid element:













, 1 





(2)

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

580

Figure 1: Visual representation of a) location-based, b)

velocity-based and c) distance-variation-based cluster

criterion.

Distance Criterion. If two feature points, a and b,

do not change their distance d(a, b) to each other

over time, as defined in equation 3, they are also

likely to be located on the same rigid element:







,















,







 



1



,



1









(3)

A visual representation of these criteria is

presented in Figure 1. Here the three different

distance measurements are applied to one, marked

feature point. The distance is shown by the

brightness of the related feature points. In Figure 1

b) the motion vector intensity is additionally

displayed by the size of the feature point. Depending

on the distance criterion, different feature regions

are highlighted. Whereas the location-based distance

in Figure 1a) is comprehensible, we can see that the

distance measurement for the velocity- (Figure 1b)

and distance-variation-based measurement (Figure

1c) shows a more structural result, where the

highlighted regions mainly belong to currently rigid

parts.

4 MOTION-BASED CLUSTERING

For the tracking and clustering of feature points the

here presented approach proceeds as follows: For the

detection and tracking of motion features, we used a

motion based feature tracking approach described in

(Koehler, 2008), which is mainly based on the

pyramidal implementation of the KLT feature

tracking method described in (Bouget, 2002),

following the 'good features to track' method of Shi

and Tomasi (Shi, 1994) and applied this to a set of

stereo images. Then, the 3D position of the feature

points is reconstructed and the result is a sparse 3D

cloud of feature points, which are tracked over time.

So it is also possible to apply time-based criteria e.g.

the velocity and relative distance over time etc. The

clustering is done for every single frame without the

integration of precedent clustering results. So every

frame is treated separately.

The criteria mentioned above, mean position,

velocity and distance variance, are calculated for

every 3D feature point. Then it is measured how

much these features criteria f, e.g. the mean position,

velocity or distance deviate from one feature point to

the others. The deviation is computed as the

Euclidean distance between pairs of feature

primitives f

and f

described in equation 4.



































(4)

Figure 2: Clustering results for a) location-, b) velocity-

and c) distance-variation-based cluster criterion.

MOTION-BASED FEATURE CLUSTERING FOR ARTICULATED BODY TRACKING

581

Then, the clustering is done by arranging the

resulting deviations d(f

) in a hierarchical cluster

tree by preserving the minimum sum of squares of

the distances between all cluster elements c

in the

cluster C and its centre point  (see equ. 5).

















(5)

A fixed number of clusters are constructed from

the resulting cluster tree by combining them with

respect to the minimum distance criterion, whereas

the linkage distance between two clusters C

and C

with the number of elements n

and n

and the

centre points 



and 



is defined in equation 6 as:











,





 

















,





















(6)

Examples for the results of the different criteria

can be seen in Figure 2.

5 RESULTS

The approach has been tested on 12 stereo videos

captured by a BumbleBee stereo camera with 20 fps

and a resolution of 640x480px with 12 motion

variations with duration from 5 - 20 sec. To get

ground truth for the requested clustering, we labelled

the features of 200 images by hand, defining 10

clusters representing the significant rigid parts of the

human body as shown in Figure 3.

To evaluate the performance, the clustering

correctness for the described criteria, local distance

and velocity as well as distance variation has been

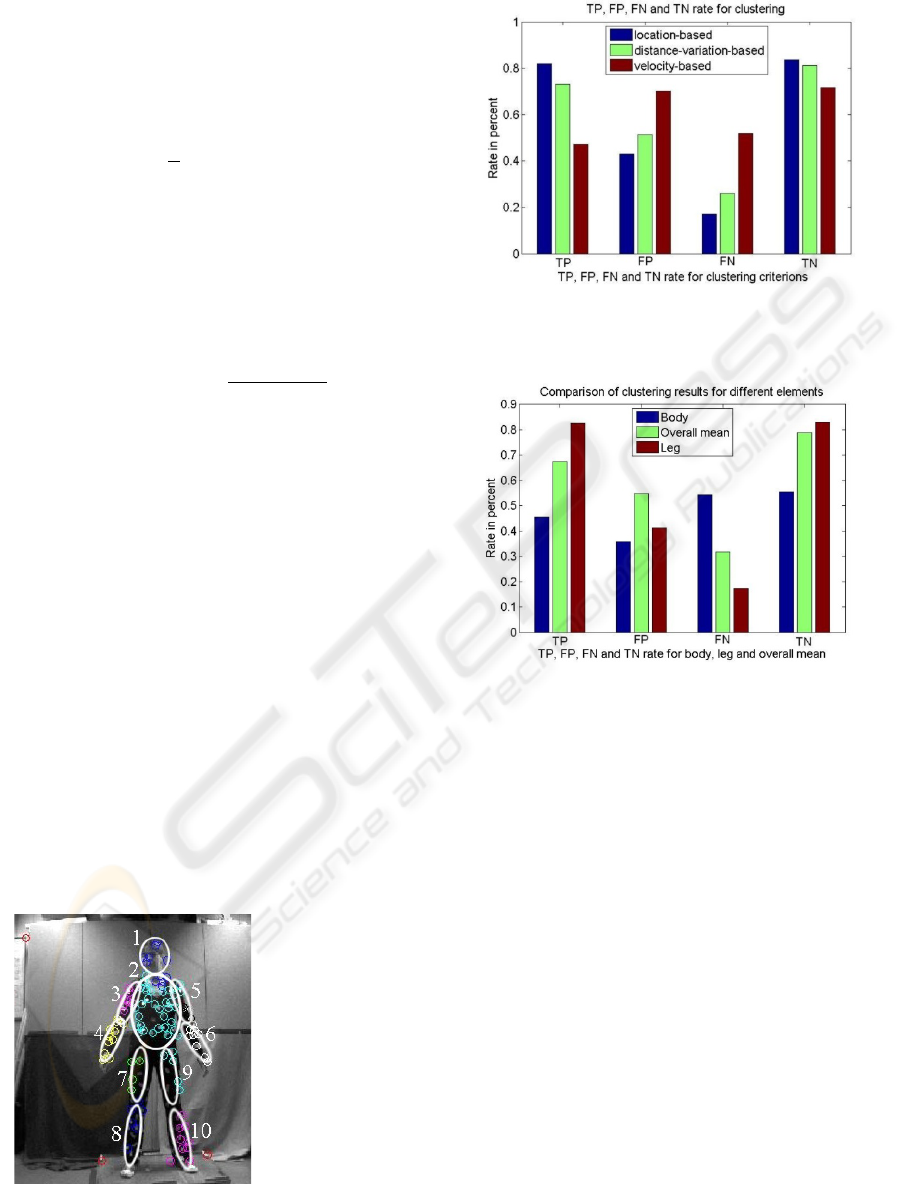
analyzed. The mean results of the true-positive,

false-positive, false-negative and true negative rate

for the different criteria are shown in Figure 4.

1. head

2. body

3. upper right arm

4. lower right arm

5. upper left arm

6. lower left arm

7. upper right leg

8. lower right leg

9. upper left leg

10. lower left leg

Figure 3: Ground truth for the evaluation of clustering and

corresponding labelling of body segments.

Figure 4: Overall true-positive, false-positive, false-

negative and true negative rate for location-based,

velocity-based and distance variation based clustering.

Figure 5: True-positive, false-positive, false-negative and

true negative rate for different anatomical groups of

clusters.

There is usually a high true-positive rate for the

location-based as well as for the distance-variation-

based clustering. Their mean true-positive rate over

all body segments is 82.00 % for the location-based

clustering and 81.37% much higher than the rate of

the velocity based clustering which lies at 47.34%.

Concerning the specificity of the clustering, the

proportion of false-positive matches is very high.

Here the tendency of the true positive rate repeats

with a much better result of 42.87% and 51.40% for

location-based and distance-variation-based

clustering than for velocity-based clustering

(70.23%). The results for the false-negative rates are

in the best case for location based clustering at

17.20% (26.03% and 51.87% for distance-variation

and velocity-based clustering). So we can see a

tendency for under rather than for over

segmentation.

It is also important to remark the qualitative

differences of clustering correctness between the

different body segments. As can be seen in Figure 5,

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

582

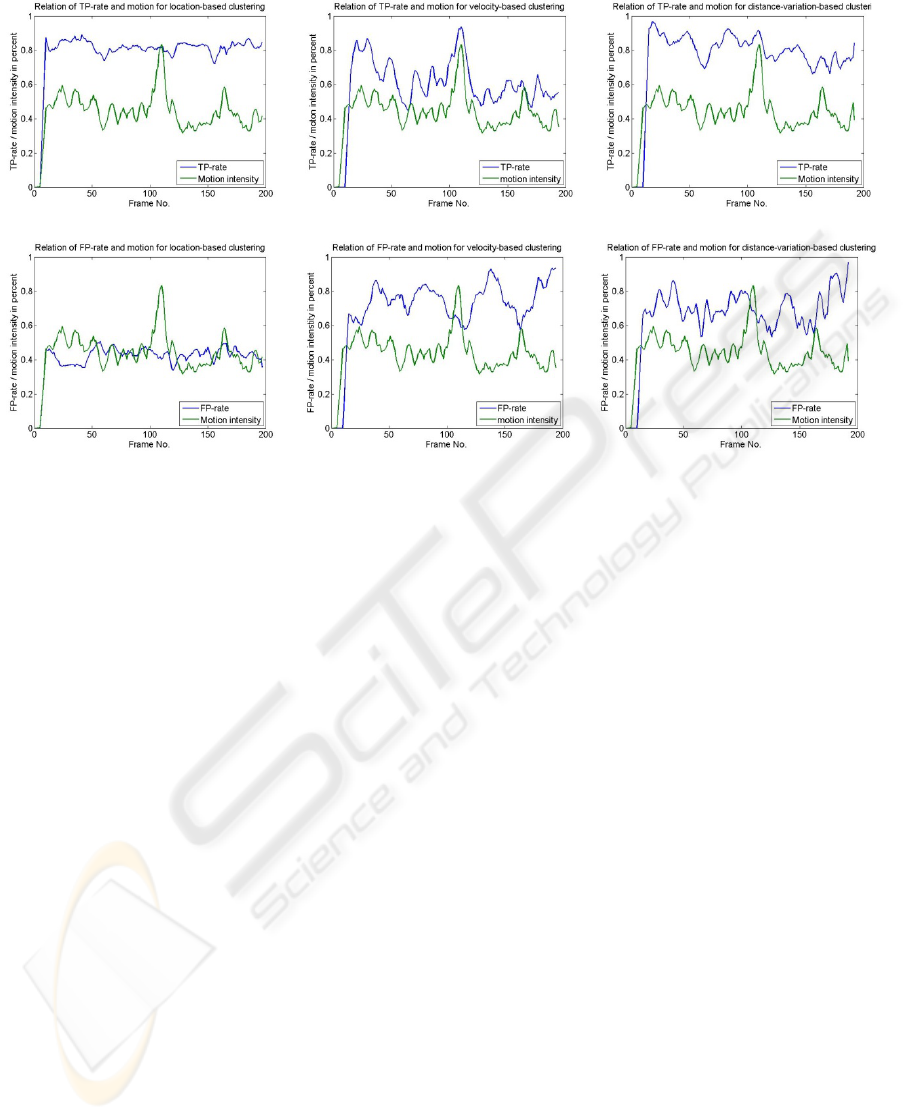
(a) (c) (e)

(b)

(d)

(f)

Figure 6: Relation of true-positive rate and motion intensity and false-positive rate and motion intensity for position based

clustering, Figure a) and b), velocity based clustering, Figure c) and d) and distance variation based clustering, Figure e)

and f). Especially for velocity based clustering, Figure c) and d), high motion intensity leads to an increase of the true-

positive rate and to a decrease of the false positive rate.

the mean true-positive rates for the upper and lower

extremities are usually over 80% whereas the head

and especially the torso tend to show a significantly

lower mean true-positive rate. This is mainly caused

by the fact that the torso is often segmented into two

or three different clusters. It usually divides into an

upper and a lower part, defining a pelvis segment

and a chest segment. The chest segment is,

depending on the actual motion sometimes also

divided into a left and right part, mainly because the

motion of the chest muscles usually support the

motion of the upper arm, so that they form two

independent segments. This peculiarity has not been

taken into account for the here presented evaluation

but should be respected in the future, especially

when it comes to the definition of an underlying

motion model.

Considering that only motion based criteria are

used, it is easy to see that the evaluation will fail

sometimes, e.g. if the person stands still, just

because there would not be any meaningful input

data when nothing moves. So, it is important to

know under which conditions a clustering would

conform to appropriate motion requirements.

So is the outstanding position of velocity-based

clustering in the overall correctness evaluation

(Figure 4) mainly based on the fact that it depends

on a certain amount of motion in the image. So, the

more features are moving in the image, the more

precise this method works. On the other hand side,

when there are only few moving features in the

image, this method usually fails. This close relation

between motion and the amount of true-positive and

true-negative features is display in Figure 6c) and d).

It is clear to see, that high motion intensity also leads

to an increase of the true-positive rate and to a

decrease of the false positive rate and vice versa,

whereas e.g. the location-based clustering is not

affected by the motion intensity (Figure 6a) and b)).

Concerning the reliability of clustering, we can see

that frames with a high proportion of moving feature

usually also have a equal or even higher specificity

of clustering (Figure 6, all) than those with only few

moving features. So, moving elements in an image

usually improve the overall clustering results. This is

comprehensible, considering the fact that especially

the distance-variation-based and even more the

velocity-based clustering depend on temporal

interpretation of the data.

For a further combination of the different

criteria, it can be useful to take advantage of this

characteristic by integrating the motion intensity as

an additional factor. This allows to concentrate on

the results of location-based clustering, when there

MOTION-BASED FEATURE CLUSTERING FOR ARTICULATED BODY TRACKING

583

is only low motion intensity and to integrate

distance-variation- and velocity-based clustering

when the motion intensity increases as well as to

estimate the reliability of the actual result, which

could be useful for subsequent processing.

6 CONCLUSIONS

We presented three different feature clustering

methods and evaluated them with respect to their

applicability for articulated body tracking. We

showed that moving features can be clustered just by

their local and temporal properties without any

additional image information and so, that the feature

motion can allow determining the structure of the

underlying e.g. rigid or articulated body. The results

showed that an acceptable correctness can be

archived by the presented cluster techniques,

according to various circumstances. The here

presented evaluation can serve as a basis to combine

the strong points of every cluster criterion. This

becomes important with regarding further

development up to a consistent cluster tracking for

longer motion sequences, but also regarding e.g. the

connection of the feature clusters in order to define

an underlying articulated motion model.

So, the here presented alignment and grouping of

features provides a basis for the reconstruction of

complex structures and their recognition.

ACKNOWLEDGEMENTS

This work was supported by the grant from the

Ministry of Science, Research and the Arts of

Baden-Württemberg, Germany.

REFERENCES

Aggarwal, J.K., Cai, Q., 1999. Human Motion Analysis: A

Review. In Computer Vision and Image

Understanding, Vol. 73, No. 3, pp. 428-440.

Aggarwal, J.K., Cai, Q., Liao, W., Sabata, B., 1994.

Articulated and elastic non-rigid motion: A review. In

Proc. IEEE Workshop on Motion of Non-Rigid and

Articulated Objects, pp 2-14.

Bouguet, J.-Y., 2002. Pyramidal implementation of the

Lucas Kanade feature tracker, description of the

algorithm. Technical report, Intel Corporation.

Cedras, C., Shah, M. 1994. A Survey of Motion Analysis

from Moving Light Displays. In IEEE Conf. on

Computer Vision and Pattern Recognition, pp. 214-

221.

Corazza, S., Mündermann, L., Andriacchi, T., 2007. A

framework for the functional identification of joint

centers using markerless motion capture, Validation

For The Hip Joint. In Journal of Biomechanics

Giese, M. A., Poggio, T., 2003. Neural mechanisms for

the recognition of biological movements and action. In

Nature Reviews Neuroscience, Vol. 4, pp. 179-192.

Holstein, H., Li, B., 2002. Low Density Feature Point

Matching for Articulated Pose Identification. In

British Machine Vision Conference 2002, pp 678 - 687

Johansson, G., 1973. Visual perception of biological

motion and a model for its analysis. In Perception &

Psychophysics, Vol. 14, No. 2, pp. 201 - 211.

Koehler, H., Pruzinec, M., Feldmann, T., Woerner, A.,

2008. Automatic Human Model Parametrization From

3D Marker Data For Motion Recognition. In Int. Conf.

in Central Europe on Computer Graphics,

Visualization and Computer Vision, Pilsen, 2008

Moeslund, T.B., Granum, E., 2001. A survey of computer

vision-based human motion capture. In Computer

Vision and Image Understanding, Vol. 81, No. 3, pp.

231-268.

Moeslund, T.B., Hilton. A., Krüger, V., 2006. A survey of

advances in vision-based human motion capture and

analysis. In Computer Vision and Image

Understanding, Vol. 104 , No. 2, pp. 90 – 126.

Nicolescu, M., Medioni, G., 2002. Perceptual Grouping

from Motion Cues Using Tensor Voting in 4-D. In

European Conf. on Computer Vision, LNCS 2352, pp.

423 - 437

Shi, J., Tomasi, C., 1994. Good Features to Track. In IEEE

Conf. on Computer Vision and Pattern Recognition,

pp. 593 - 600.

Silaghi, M.-C., Plänkers, R., Boulic, R., Fua, P.,

Thalmann, D., 1998. Local and Global Skeleton

Fitting Techniques for Optical Motion Capture. In

Proc. of the International Workshop on Modelling and

Motion Capture Techniques for Virtual Environments,

LNCS 1537, pp. 26-40.

Song, Y., Goncalves, L., Di Bernardo, E., Perona,P., 1999.

Monocular Perception of Biological Motion -

Detection and Labeling. In Proc. of the Int. Conf. on

Computer Vision, Vol. 2, pp. 805-812.

Song, Y., Goncalves, L., Perona, P., 2003. Unsupervised

Learning of Human Motion. In IEEE Transactions on

Pattern Analysis and Machine Intelligence, Vol. 25 ,

No. 7, pp. 814-827

Tomasi, C., and Kanade, T., 1991. Detection and tracking

of point features.

Technical Report, School of

Computer Science, Carnegie Mellon University

Ullman, S., 1983. Computational Studies in the

Interpretation of Structure and Motion: Summary and

Extension. In Human and Machine Vision, Academic

Press

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

584