ADAPTATIVE CUBICAL GRID FOR ISOSURFACE EXTRACTION

John Congote

, Aitor Moreno

, I˜nigo Barandiaran

, Javier Barandiaran

and Oscar E. Ruiz

CAD/CAM/CAE Laboratory, EAFIT University, Medell´ın, Colombia

VICOMTech, San Sebastian, Spain

Keywords:

Adaptive isosurface extraction, Adaptive tessellation, Isosurfaces, Volume warping, Marching cubes.

Abstract:

This work proposes a variation on the Marching Cubes algorithm, where the goal is to represent implicit

functions with higher resolution and better graphical quality using the same grid size. The proposed algorithm

displaces the vertices of the cubes iteratively until the stop condition is achieved. After each iteration, the

difference between the implicit and the explicit representations are reduced, and when the algorithm ﬁnishes,

the implicit surface representation using the modiﬁed cubical grid is more detailed, as the results shall conﬁrm.

The proposed algorithm corrects some topological problems that may appear in the discretisation process using

the original grid.

1 INTRODUCTION

Surface representation from scalar functions is an

active research topic in different ﬁelds of computer

graphics such as medical visualisation of Magnetic

Resonance Imaging (MRI) and Computer Tomogra-

phy (CT) (Krek, 2005). This representation is also

widely used as an intermediate step for several graph-

ical processes (Oscar E. Ruiz, 2005), such as mesh

reconstruction from point clouds or track planning.

The representation of a scalar function in 3D is known

as implicit representation and is generated using con-

tinuous algebraic iso-surfaces, radial basis functions

(Carr et al., 2001) (Morse et al., 2005), signed dis-

tance transform (Frisken et al., 2000) or discrete vox-

elisations.

The implicit functions are frequently represented

as a discrete cubical grid where each vertex has the

value of the function. The Marching Cubes algorithm

(MC) (Lorensen and Cline, 1987) takes the cubical

grid to create an explicit representation of the implicit

surface. The MC algorithm has been widely stud-

ied as has been demonstrated by Newman (Newman

and Yi, 2006). The output of the MC algorithm is

an explicit surface represented as a set of connected

triangles known as a polygonal representation. The

original results of the MC algorithm presented several

topological problems as demonstrated by Chernyaev

(Chernyaev, 1995) and have already been solved by

Lewiner (Lewiner et al., 2003).

Figure 1: Optimised Grid with 20

cubes representing the

bunny.

The MC algorithm divides the space in a regular

cubical grid. For each cube, a triangular representa-

tion is calculated, which are then joined to obtain the

explicit representation of the surface. This procedure

is highly parallel because each cube can be processed

separately without signiﬁcant interdependencies. The

resolution of the generated polygonal surface depends

directly on the input grid size. In order to increase the

resolution of the polygonal surface it is necessary to

Congote J., Moreno A., Barandiaran I., Barandiaran J. and E. Ruiz O. (2009).

ADAPTATIVE CUBICAL GRID FOR ISOSURFACE EXTRACTION.

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 21-26

DOI: 10.5220/0001786200210026

 SciTePress

increase the number of cubes in the grid, increasing

the amount of memory required to store the values of

the grid.

Alternative methods to the MC algorithm intro-

duce the concept of generating multi-resolution grids,

creating nested sub-grids inside the original grid. The

spatial subdivision using octrees or recursive tetrahe-

dral subdivision techniques are also used in the opti-

misation of iso-surface representations. The common

characteristic of these types of methods is that they

are based on adding more cells efﬁciently, to ensure a

higher resolution in the ﬁnal representation.

This work is structured as follows: In Section 2, a

review of some of the best known MC algorithm vari-

ations is given. Section 3 describes the methodologi-

cal aspects behind the proposed algorithm. In Section

4 details the results of testing the algorithm with a set

of implicit functions. Finally, conclusions and future

work are discussed in Section 5.

2 RELATED WORK

Marching Cubes (MC) (Lorensen and Cline, 1987)

has been the de facto standard algorithm for the

process generating of explicit representations of iso-

surfaces from scalar functions or its implicit deﬁnition

The MC algorithm takes as an input a regular scalar

volumetric data set, having a scalar value residing at

each lattice point of a rectilinear lattice in 3D space.

The enclosed volume in the region of interest is sub-

divided into a regular grid of cubes. Each vertex of all

cubes in the grid is set the value of the implicit func-

tion evaluated at the vertex coordinates. Depending

on the sign of each vertex, a cube has 256 (2

) pos-

sible combinations, but using geometrical properties,

such as rotations and reﬂections, the ﬁnal number of

combinations is reduced to 15 possibilities. These 15

surface triangulations are stored in Look-Up Tables

(LUT) for speed reasons. The ﬁnal vertices of the

triangular mesh are calculated using linear interpola-

tion between the values assigned to the vertices of the

cube. This polygonal mesh representation is ideally

suited to the current generation of graphic hardware

because it has been optimised to this type of input.

MC variations were developed to enhance the res-

olution of the generated explicit surfaces, allowing the

representation of geometrical details lost during MC

discretisation process. Weber (Weber et al., 2001)

proposes a multi-grid method. Inside an initial grid,

a nested grid is created to add more resolution in that

region. This methodology is suitable to be used re-

cursively, adding more detail to conﬂictive regions.

In the ﬁnal stage, the explicit surface is created by

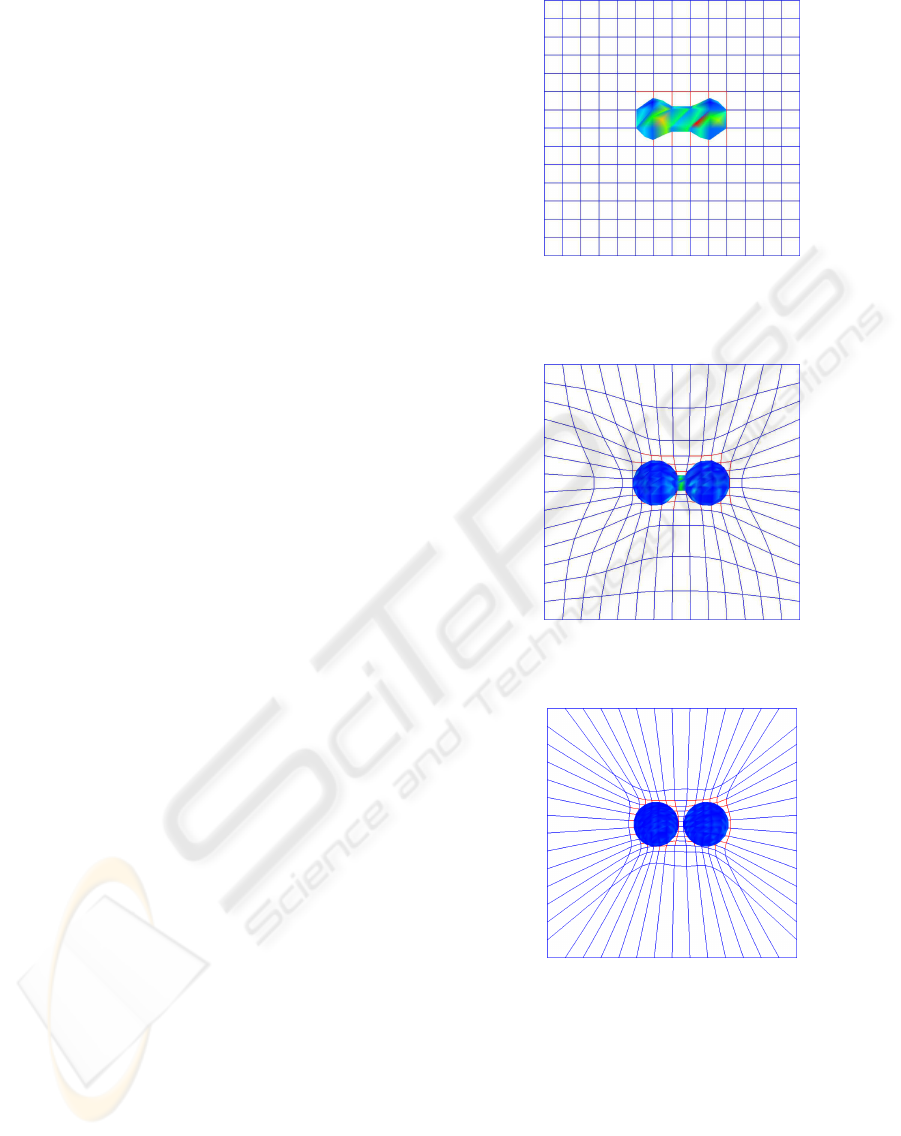
(a) Original Grid. The two spheres

are displayed as a singular object

due to the poor resolution in the re-

gion.

(b) Intermediate Grid. Both spheres

are displayed well, but are still

joined.

displays two well shaped and sepa-

rated spheres with the same number

of cubes in the grid.

Figure 2: 2D slides representing three different states in the

evolution of the algorithm of two nearby spheres.

joining all the reconstructed polygonal surfaces.

It is necessary to generate a special polygonisa-

tion in the joints between the grid and the sub-grids

to avoid the apparition of cracks or artifacts. This

method has a higher memory demand to store the new

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

values of the nested-grid.

An alternative method to reﬁne selected region

of interest is the octree subdivision (Shekhar et al.,

1996). This method generates an octree in the re-

gion of existence of the function, creating a poly-

gonisation of each octree cell. One of the ﬂaws of

this method is the generation of cracks in the regions

with different resolutions. This problem is solve with

the Dual Marching Cubes method (Schaefer and War-

ren, 2004) and implemented for algebraic functions

by Pavia (Paiva et al., 2006)

The octree subdivision method produces edges

with more than two vertices, which can be overcome

by changing the methodology of the subdivision. In-

stead of using cubes, tetrahedrons were used to subdi-

vide the grid, without creating nodes in the middle of

the edges (Kimura et al., 2004). This method recur-

sively subdivides the space into tetrahedrons.

The previous methodologies increment the num-

ber of cells of the grid in order to achieve more reso-

lution in the regions of interest. Balmelli (Balmelli

et al., 2002) presented an algorithm based on the

movement of the grid to a deﬁned region of interest

using a warping function. The result is a new grid

with the same number of cells, but with higher reso-

lution in the desired region.

Our method is also based on the displacement of

the vertices of the grid, obtaining dense distribution

of vertices near to the iso-surface. (see Figure 2)

3 METHODOLOGY

The proposed algorithm is presented as a modiﬁcation

of the MC algorithm. The principal goal is the gen-

eration of more detailed approximations of the given

implicit surfaces with the same grid resolution.

Applying a selective displacement to the vertices

of the grid, the algorithm increases the number of

cells containing the iso-surface. In order to avoid self-

intersections and to preserve the topological structure

of the grid, the vertices are translated in the direction

of the surface. The displacement to be applied to each

vertex is calculated iteratively until a stop condition is

satisﬁed.

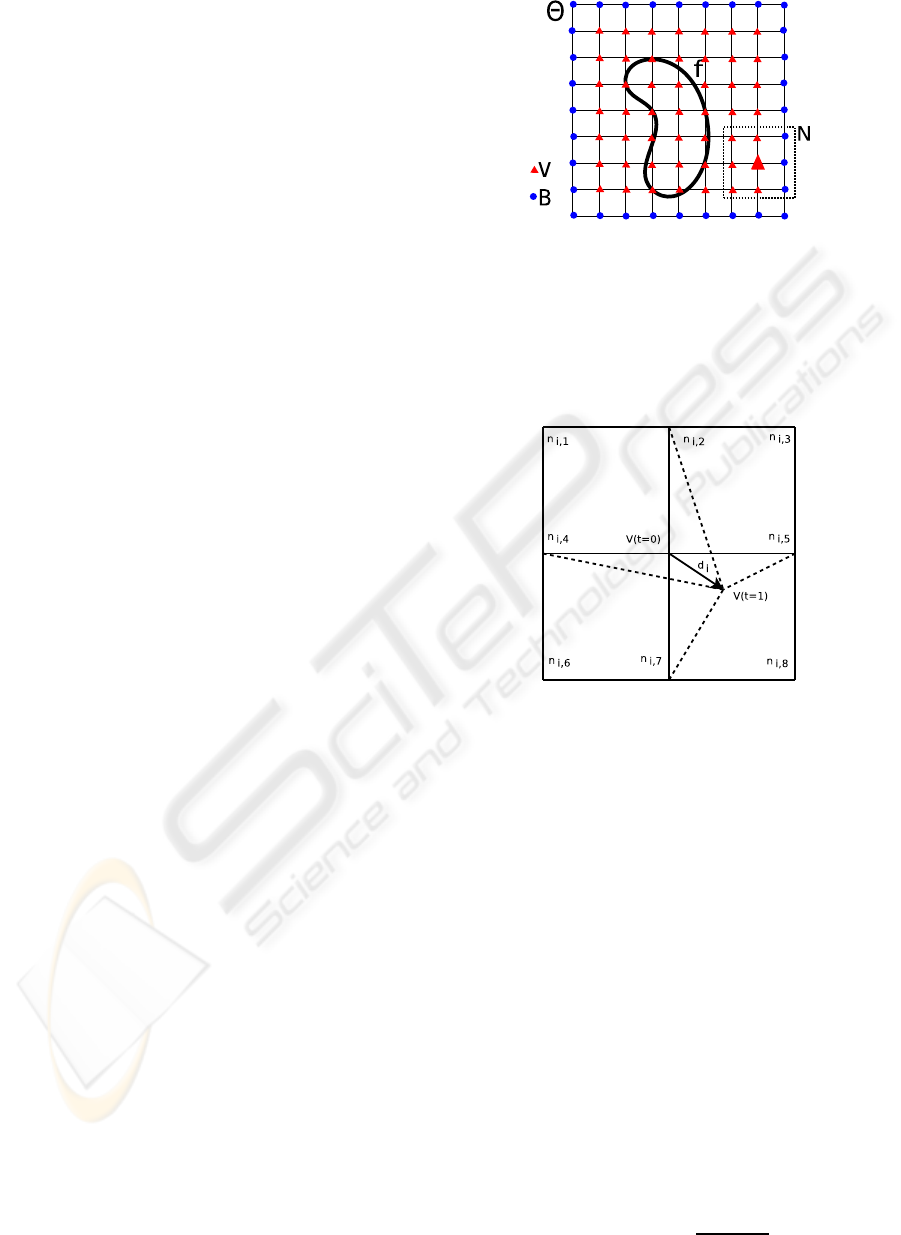
Let be Θ a rectangular prism tessellated as a cu-

bical honeycomb, W the vertices of Θ [Eq. 1], B the

boundary vertices of Θ [Eq. 2], and V the inner ver-

tices of Θ [Eq. 3]. For each vertex v

∈ V, a N

set

is deﬁned as the 26 adjacent vertices to v

, denoting

each adjacent vertex as n

i, j

[Eq. 4]. (see Figure 3)

W = {w

∈ Θ} (1)

B = {b

∈ δΘ} (2)

Figure 3: Grid nomenclature, Θ cubical grid, f(x,y,z) = 0

implicit function, N vertex neightboor, V vertices inside the

grid, B vertices at the boundary of the grid.

V = W − B (3)

= {n

i, j

is jth neighbourgh of v

} (4)

Figure 4: two consecutives iterations are show where the

vertex v is moved between the iterations t = 0 and t = 1.

The new conﬁguration of the grid is shown as dotted lines.

The proposed algorithm is an iterative process. In

each iteration, each vertex v

of the grid Θ is trans-

lated by a d

distance vector, obtaining a new conﬁg-

uration of Θ, where i) the topological connections of

the grid are preserved, ii) the number of cells con-

taining patches of f are greater than, or equal to, the

previous value, and iii) the total displacement [Eq. 7]

of the grid is lower and is used as the stop condition

of the algorithm when it reach a value ∆(see Figure

4).

The distance vector d

is calculated as shown in

[Eq. 6] and it can be seen as the resultant force of

each neighbouring vertex scaled by the value of f at

the position of each vertex. In order to limit the max-

imum displacement of the vertices and to guarantee

the topological order of Θ, the distance vector d

clamped in the interval expressed in [Eq. 5]

0 ≤ |d

| ≤ MIN



i, j

− v



(5)

ADAPTATIVE CUBICAL GRID FOR ISOSURFACE EXTRACTION

∑

i, j

− v

1+ | f(n

i, j

) + f(v

(6)

∑

| ≥ ∆ (7)

The algorithm stops when the sum of the distances

added to all the vertices in the previous iteration is

less that a given threshold ∆ [Eq. 7] (see Algorithm

1).

Algorithm 1: Vertex Displacement Pseudo-

algorithm. |x| represents the magnitude of x, ¯v

represents the normalised vector of v.

repeat

s := 0;

foreach Vertex v

∑

i, j

−v

1+| f (n

i, j

)+ f (v

;

mindist := MIN



i, j

−v



;

CLAMP(|d

|,0.0, mindist);

:= v

+ d

;

s := s+ |d

end

until s ≥ ∆ ;

4 RESULTS

Figure 5: Two balls in different positions with a scalar func-

tion as the distance transform, representing the behaviour of

the algorithm with different objects in the space.

The proposed algorithm was tested with a set of im-

plicit functions as distance transforms (see Figure 5)

and algebraic functions (see Figure 6(a)). For demon-

stration purposes, the number of cells has been chosen

to be very low to aid in the visual detection of the im-

provements produced by the algorithm. For the visu-

alisation process we use Marching Tetrahedra because

Table 1: Quality is measured as the average distance be-

tween the mesh vertices and the real surfaces. The col-

muns 1 and 2 represent the quality of the bunny model

(MC. QLTY.) using the given cubical grid size (GS

) with

the standard MC algorithm. The columns 3 and 4 shows

the quality (AMC. QLTY.) using the given cubical grid size

(GS

) with the proposed algorithm after 30 iterations. The

quality values (columns 2 and 3) have been aligned to be as

equal as possible, showing that to achieve a target quality,

the grid size using the proposed algorithm is less than the

required using the standard MC algorithm.

MC. QLTY. AMC. QLTY. GS

10 0.958555 - -

20 0.369976 0.32257 10

30 0.188298 0.186994 20

40 0.129414 0.127588 30

50 0.094878 0.092761 40

it produces correct topological representation of the

iso-surface, and allows the identiﬁcation of the topo-

logical correctness of the algorithm.

The obtained results of the algorithm are visually

noticeable, as is shown in Figure 6. Without using

the algorithm, the two spheres model is perceived as

a single object (see Figure 2). In an intermediate state

the spheres are still joined, but their shapes are more

rounded. In the ﬁnal state, when the algorithm con-

verges, both spheres are separated correctly, each one

being rendered as a near perfect sphere. Thus, using

the same grid resolution and the proposed algorithm,

the resolution of the results has been increased.

The proposed algorithm iteratively increases the

number of cells containing the surface, adding more

detail to the new representation. Figure 6(b) shows

the incremental evolution of such a number of cubes

containing the surface, tending toward a doubling of

the number. The average distance triangulation ver-

tices to the original surface was calculated as pre-

sented in table 1. The proposed algorithm can rep-

resent the surface with a good quality with a fraction

of the amount of cells required with the original MC

algorithm.

The total displacement of the vertices in each iter-

ation is decreasing rapidly toward zero after a number

of iterations as show in the Figure 6(c). Despite the

seemingly high number of iterations, the algorithm

is executed only once for static functions, and can

be processed in the background. Even when the im-

plicit function is a time variant, the cubical grid can

be reused as the input cubical grid for the next algo-

rithm execution. When the implicit function changes

smoothly, the algorithm quickly re-converges after

just a few iterations signiﬁcantly reducing the com-

putational effort.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

(a) Algebraic function rendered

with an optimised grid

(b) Cube increment (Y axis) vs. Iter-

ation evolution (X axis)

axis) vs. Iteration evolution (X axis)

Figure 6: Grid evolution for an algebraic function, comparing the number of cubes which contains the iso-surface and the

total displacement of the vertices plotted against the stage of execution of the algorithm.

5 CONCLUSIONS AND FUTURE

WORK

Our proposed iterative algorithm has shown signif-

icant advantages in the representation of distance

transform functions. With the same grid size, it allows

a better resolution by displacing the vertices of the

cube grids towards the surface, increasing the number

of cells containing the surface.

The algorithm was tested with algebraic functions,

representing distance transform of the models. The

generated scalar ﬁeld has been selected to avoid the

creation of regions of false interest, which are for

static images in which these regions are not used.

The number of iterations is directly related to the

chosen value ∆ as it is the stop condition. The algo-

rithm will continuously displace the cube vertices un-

til the accumulated displacement in a single iteration

is less than ∆. In the results, it can be seen that this

accumulated distance convergesquickly to the desired

value. This behaviour is very convenient to represent

time varying scalar functions like 3D videos, where

the function itself is continuously changing. In this

context, the algorithm will iterate until a good rep-

resentation of the surface is obtained. If the surface

varies smoothly, the cube grid will be continuously

and quickly readapted by running a few iterations of

the presented algorithm. As the surface changes may

be assumed to be small, the number of iterations un-

til a new ﬁnal condition is achieved will be low. The

obtained results will be a better real-time surface rep-

resentation using a coarser cube grid.

6 ACKNOWLEDGEMENTS

This work has been partially supported by the Spanish

Administration agency CDTI, under project CENIT-

VISION 2007-1007. CAD/CAM/CAE Laboratory -

EAFIT University and the Colombian Council for

Science and Technology -Colciencias-. The bunny

model is courtesy of the Stanford Computer Graph-

ics Laboratory.

REFERENCES

Balmelli, L., Morris, C. J., Taubin, G., and Bernardini, F.

(2002). Volume warping for adaptive isosurface ex-

traction. In Proceedings of the conference on Visual-

ization 02, pages 467–474. IEEE Computer Society.

Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J.,

Fright, W. R., McCallum, B. C., and Evans, T. R.

(2001). Reconstruction and representation of 3d ob-

jects with radial basis functions. In SIGGRAPH ’01:

Proceedings of the 28th annual conference on Com-

puter graphics and interactive techniques, pages 67–

76, New York, NY, USA. ACM.

Chernyaev, E. (1995). Marching cubes 33: Construction

of topologically correct isosurfaces. Technical report,

Technical Report CERN CN 95-17.

Frisken, S. F., Frisken, S. F., Perry, R. N., Perry, R. N.,

Rockwood, A. P., Rockwood, A. P., Jones, T. R., and

Jones, T. R. (2000). Adaptively sampled distance

ﬁelds: A general representation of shape for computer

graphics. pages 249–254.

Kimura, A., Takama, Y., Yamazoe, Y., Tanaka, S., and

Tanaka, H. T. (2004). Parallel volume segmentation

with tetrahedral adaptive grid. ICPR, 02:281–286.

Krek, P. (2005). Flow reduction marching cubes algo-

rithm. In Proceedings of ICCVG 2004, pages 100–

106. Springer Verlag.

ADAPTATIVE CUBICAL GRID FOR ISOSURFACE EXTRACTION

Lewiner, T., Lopes, H., Vieira, A., and Tavares, G. (2003).

Efﬁcient implementation of marching cubes’ cases

with topological guarantees. Journal of Graphics

Tools, 8(2):1–15.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3d surface construction algorithm.

SIGGRAPH Comput. Graph., 21(4):169–169.

Morse, B. S., Yoo, T. S., Rheingans, P., Chen, D. T., and

Subramanian, K. R. (2005). Interpolating implicit

surfaces from scattered surface data using compactly

supported radial basis functions. In SIGGRAPH ’05:

ACM SIGGRAPH 2005 Courses, page 78, New York,

NY, USA. ACM.

Newman, T. S. and Yi, H. (2006). A survey of the marching

cubes algorithm. Computers & Graphics, 30(5):854–

879.

Oscar E. Ruiz, Miguel Granados, C. C. (2005). Fea-driven

geometric modelling for meshless methods. In Virtual

Concept 2005, pages 1–8.

Paiva, A., Lopes, H., Lewiner, T., and de Figueiredo, L. H.

(2006). Robust adaptive meshes for implicit surfaces.

SIBGRAPI, 0:205–212.

Schaefer, S. and Warren, J. (2004). Dual marching cubes:

Primal contouring of dual grids. In PG ’04: Proceed-

ings of the Computer Graphics and Applications, 12th

Paciﬁc Conference, pages 70–76, Washington, DC,

USA. IEEE Computer Society.

Shekhar, R., Fayyad, E., Yagel, R., and Cornhill, J. F.

(1996). Octree-based decimation of marching cubes

surfaces. In VIS ’96: Proceedings of the 7th confer-

ence on Visualization ’96, pages 335–ff., Los Alami-

tos, CA, USA. IEEE Computer Society Press.

Weber, G. H., Kreylos, O., Ligocki, T. J., Shalf, J. M.,

Hamann, B., and Joy, K. I. (2001). Extraction of

crack-free isosurfaces from adaptive mesh reﬁnement

data. In Data Visualization 2001 (Proceedings of Vis-

Sym ’01), pages 25–34. Springer Verlag.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications