
A METHOD FOR 3D MORPHING USING SLICES
Shamima Yasmin and Abdullah Zawawi Talib
School of Computer Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
Keywords: Morphing, Oriented Bounding Box (OBB), Alignment, Boundary Interpolation, Surface Reconstruction.
Abstract: 3-D morphing, in its simplest definition, is shape transformation between a pair of objects i.e. source and
target, by gradual, continuous and simultaneous dissolvement of the shape of source object to its target and
vice versa resulting in a number of intermediate shapes. Many algorithms have been developed for this
purpose with each one having its own speciality. In this paper, a novel algorithm is presented which is based
on slices. The technique originates from the concept of reducing a 3-D object to a number of slices in 2D
plane. In the algorithm, all of the 2D slices may not be oriented in either x, y, z or in a particular direction.
Orientation and rotation of the slices within a single body can be varied from one slice to another based on
the alignment of the object. Oriented Bounding Box (OBB) is used to determine the orientation of the
object. The advantages of the proposed method i.e. minimal user input, flexibility, dynamism and ease of
implementing over other 3D morphing algorithms are also discussed.
1 INTRODUCTION
Starting from the late eighties until the end of
nineties numerous algorithms on 3D morphing have
been developed. Now morphing has become an
indispensable tool in 3D animation industry. Not just
for the purpose of transforming from one shape to
another, morphing is also useful in incorporating
characteristics of different bodies in different
proportions to the morphed output.
In this paper a morphing algorithm which takes
into account of orientation and distortion of the
object is presented. Object is cut into slices along its
alignment. Oriented Bounding Box (OBB) is used to
determine the initial alignment of the object. The
more dense the slices, the more accurate is the
alignment (though there is an optimal limit on how
dense the slices could be). For all kind of objects,
this method works with minimal user input. The
simplicity, accuracy, versatility, flexibility and
extendibility of the algorithm meet all the criteria of
a good and efficient morphing algorithm based on
our survey on a number of morphing algorithms.
2 BACKGROUND
Depending on the various approaches, existing
morphing algorithms can be classified into the
following categories: a) Surface-based morphing:
consists of continuous mapping of small pieces of
polygonal surfaces of source object to those of target
object; b) Volume-based morphing: modifies voxel
values of a volume data set for smooth transition
between source and target shapes.
Surface-based approach uses user-defined
control fields such as point fields, line fields etc.
during morphing to map key features of source and
target objects ((Hong, 1988), (Parent, 1992),
(Lazarous, 1994), (Turk, 1999), (Lee, 1999)).
Surface-based methods are important because of its
ability to morph between objects of different types
of genus, but these methods also require a significant
amount of user input. Another troubling feature of
surface-based method is the problem of self-
intersection. It cannot guarantee that polygonal
surfaces will not pass through themselves, creating
self-intersecting intermediate result as found in
(Hong, 88).
Volume-based approach alleviates some of the
problems mentioned above. Among them, the
simplest approach is the cross-dissolving method
(Hughes, 1992) which at first transforms volume
data from spatial domain to frequency domain by
Fourier transform, then linearly interpolates volume
in frequency domain and again transforms back to
spatial domain. To enhance the smoothness of the
in-between volumes, Fourier transform has been
used by gradually removing high frequencies of
292
Yasmin S. and Talib A. (2009).
A METHOD FOR 3D MORPHING USING SLICES.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 292-301
DOI: 10.5220/0001786602920301
Copyright
c
SciTePress

source model, interpolating over to the low
frequencies of the second model and smoothly
adding in the high frequencies of the second model.
But Fourier transform does not localize in spatial
domain. In order to have a smooth transition, voxel
values of the entire volume are modified according
to the distance of the nearest iso-surface. This
problem can be solved by Wavelet transformation
(He, 1994), which localizes both in frequency and
spatial domain resulting in a multi-resolution fashion
so that high frequency distortion can be adjusted at
the desired level.
Both of the above mentioned methods have
difficulties in specifying slightly complex geometric
transformations such as object rotation. By relying
on the frequency information, the methods would
also have difficulties while associating with some
scalars such as colors, opacities and texture. This
problem can be alleviated by applying warping
before interpolation as found in (Lerois, 1995). Here
user-defined warp is applied on source and target
objects to resemble each other. Warped source
object and target object are then interpolated.
Instead of using point and line control fields in
3-D volume morphing, user-specified disk field
(Chen, 1996) can be used. Equal number of disks are
applied on both source and target to establish
correspondence between them. Each disk has its
own normal direction which helps in considering
distortion of the body.
Payne et al. introduces ‘Distance Volume’ mea -
sured by computing the shortest distance of each
voxel within the volume to the surface of the object.
Distance field is transformed to a function to meet
greater, equal or lesser “blobbiness” between the
source and target objects. Once the distance field for
the input surfaces are computed, interpolation is
performed in between the surfaces.
In (Breen, 2001), the way in which points on the
surface moves is used to establish connection
between source and target. Every point on the source
surface moves in the direction of the normal at that
point with a velocity proportional to the signed
distance at that point in 3-D space from target
surface and vice-versa. Those parts of source which
are outside the target contract whereas inside parts
move in the direction of surface normals and
expand.
Shape transformation using implicit function
(Turk, 1999) is constructed by reducing a 3-D
volume to a stack of 2-D slices along any of the
major axes. Implicit functions of each pair of 2-D
slices are determined using a set of constraints i.e.
location, weight, scalar values etc. The resultant 2-D
contour is established by interpolating each pair of
implicit functions and this is repeated for each pair
of slices between source and target objects along the
third axis.
From the above discussion, it is obvious that
volume-based approach has got some advantages
over surface-based approach though each approach
has its own advantages. It is imperative that we
strive to develop a new volume-based morphing
algorithm which optimizes user input, considers
rotation/orientation of rigid body during morphing
and preserves smooth transition between source and
target.
3 ALGORITHM OVERVIEW
The algorithm mainly consists of the following
major steps :
Data Traversal and Slicing of Data;
Boundary Extraction;
Boundary Projection and Boundary Interpo-
lation;
Orientation and Translation of Boundaries;
Surface Reconstruction.
3.1 Data Traversal and Slicing of Data
Source and target data are collected. The initial
orientation along which the data are subdivided in
the first step of the binary subdivision is defined
along any of the directions of the Oriented Bounding
Box (OBB) (Gottschalk, 1996). An Oriented
Bounding Box (OBB) is a bounding box that does
not necessarily align itself along the coordinate axes.
OBB is constructed from the mean and covariance
matrix of the cells and their vertices that define the
dataset. The eigen vectors of the covariance matrix
are extracted, giving a set of three orthogonal
vectors that define the alignment of the dataset.
Figure 1 shows the difference between a normal
bounding box and an oriented bounding box. No
doubt, an oriented bounding box more closely fits
the data than a normal bounding box. The purpose of
choosing the oriented bounding box is to allow
checking of the longitudinal direction of dataset
from its oriented bounding box rather than from
normal bounding box. The OBB only bounds the
“geometry” attached to the cells if the convex hull of
the cells bounds the geometry. This is done in order
A METHOD FOR 3D MORPHING USING SLICES
293

to negate the effects of the extreme distribution of
the points.
Figure 1: (a) Normal Bounding Box and (b) Oriented
Bounding Box.
Eigen vectors describe the maximum, medium
and minimum variance of concentration of point
clouds. Usually either maximum or medium direc -
tion of the eigen vectors are used as the direction of
the initial alignment. The ‘maximum’ direction
shows the maximum amount of concentration of the
cells of the data along that direction, whereas the
‘medium’ direction exhibits less amount of concen -
tration than maximum direction and the ‘minimum’
direction shows the least amount of concentration or
the least alignment of the cells along that direction.
The first subdivision takes place along a plane
centered at the center of the Oriented Bounding Box
(OBB) of the object with normal along the initial
alignment. This step, called ‘step 0’, divides the data
into two end parts. In each of the subsequent steps,
the number of slices is doubled.
In the next step i.e. ‘step 1’, each of the two end
pieces found from ‘step 0’ is wrapped with OBB and
tested whether the longitudinal direction of the
alignment of the sliced end is still within the
maximum or medium direction of the OBB. If the
alignment is still within maximum/ medium
direction, a line joining the center of the previous cut
plane and the center of the OBB is used as the
direction of the cut plane normal for the ends in that
step (Figure 2). Otherwise ends are sliced along the
cut plane normal found in the previous step which is
used for any further subdivision of the ends and in
the subsequent steps no further checking on the
alignment is done. At the end of ‘step 1’, the data is
divided into four parts i.e. two end parts and two
middle parts.
Before further subdivision of the ends, if
necessary, checking is done for the alignment of the
two sliced ends. The procedure described in ‘step 1’
is followed for further subdivision of the two ends.
For the middle parts, data is sliced along the plane
with center as the center of the OBB and normal
directed along the resultant normals of the two ends
of the middle data (Figure 2(a)). Slicing is continued
along the longitudinal direction until the desired
number of steps is reached. In each subsequent step,
the number of slices is doubled at each step. The
default longitudinal direction is the ‘maximum’
direction of the eigen vectors and the default number
of steps for binary subdivision of the data is ‘four’.
To provide more flexibility, the initial longitudinal
direction as well as the number of steps can be
defined by the user. We indicate the maximum
alignment as ‘0’, the medium alignment as ‘1’ and
the minimum as ‘2’. Therefore, the users are allowed
to vary the morphed output based on the initial
alignment. Subdivision can also be forced to happen
along any particular direction or along any of the
axes i.e. x, y or z to generate parallel slices.
(a) (b)
C2 =
N1= Line joining C1 and O1
Center
of
OBB
Figure 2: Division of (a) the End Data and (b) the Middle
Data.
The steps involved in slicing a given data with
default initial settings are depicted in Figure 3. After
reaching the desired number of steps, cut edges of
the ends are usually still a bit far from the tip. In
order to extract a proper outline of the object, ends
near the tip need to be extracted. For this purpose,
two ends are traversed along the tip. Usually no fur -
ther checking for the alignments of the two ends are
needed now as the current alignments of the sliced
ends are usually not along the maximum or the
medium direction of the OBB of the two sliced
ends. So for any further subdivision, the normal is
usually along the direction which was found at the
step before the last checking step and traversing
towards the tip is continued along that direction until
it is close enough to the tip. Now the ends are again
divided into two parts. At this stage, each of the two
end slices which were found at the end of the last
step consists of two end parts with very thin top ends
near the tips as shown at the bottom of Figure 3.
N =N2 + N3’
N2
N3’
O1 = Center o
f
Previous Cut Plane
Next cut plane is along normal
N with Center C2.
(b)
C1=
Center
of
OBB
Next cut plane is
along Normal N1
with Center C1.
(Alignment is with
-in maximum/ medi-
um)
(a)
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
294
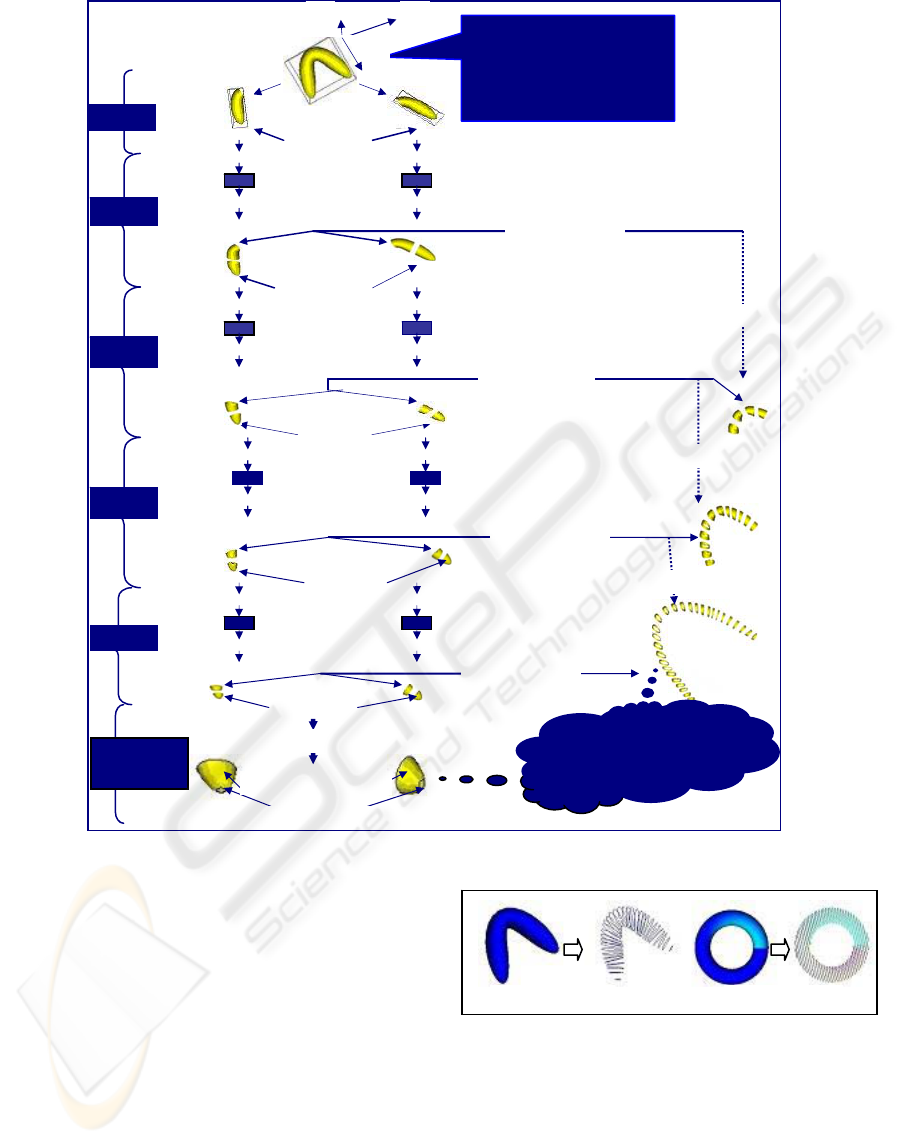
Figure 3: Traversal and Slicing of a Given Data.
3.2 Boundary Extraction
Only boundaries of the slices are extracted (Figure
4). As discussed above, in ‘step 0’, data is divided
into two parts. In each of the subsequent steps, the
number of slices are doubled. Hence in ‘step 4’,
there are 2
(4+1)
i.e. 32 slices. From 32 slices 31
boundaries can be extracted. Then boundaries at the
ends which are determined after the specified
number of steps is reached are also added. Two such
boundaries at the two ends result in a total of 33
boundaries each. Hence in ‘step 4’, the number of
extracted boundaries (for each source and target) is
computed as follows:
2
(step+1)
+ 1 = 2
(4+1)
+ 1= 2
5
+ 1 = 33
Figure 4: Extraction of Source and Target Boundaries.
3.3 Boundary Projection and
Boundary Interpolation
Both source and target boundaries are projected onto
the XZ plane and centered at the origin. Each of the
source and target boundaries are traversed along the
direction of their minimum X (X
min
) to maximum X
Initial Conditions:
1.No. of Step = 4 (default);
2. Alignment = 0 (default)
(maximum = 0, medium = 1,
minimum = 2)
2 0
2 End Parts
2 End Parts
Alig
nment
Ch
ec
ki
n
g
Di
v
i
s
i
on o
f
t
h
e
E
n
d
s
Yes
Alig
nment
Ch
ec
ki
n
g
Di
v
i
s
i
on o
f
t
h
e
E
n
d
s
Yes
Alig
nment
Ch
ec
ki
n
g
Division of the Ends
Yes
Alig
nment
Ch
ec
ki
n
g
Division of the Ends
Yes
Step 4
Alig
nment
Ch
ec
ki
n
g
Di
v
i
s
i
on o
f
t
h
e
E
n
d
s
No
Alig
nment
Ch
ec
ki
n
g
Division of the Ends
No
2EndParts
2 Thin End Parts Parts
Alig
nment
Ch
ec
ki
n
g
Division of the Ends
Yes
Alig
nment
Ch
ec
ki
n
g
Division of the Ends
Yes
2 End Parts
30 Middle Parts
14 Middle Parts
1
Determination
of Top Ends
Division of the Middle Parts
Division of the Middle Parts
Traversal alon
g
the Ti
p
2Thicker Middle Parts
2 End Parts
6 Middle Parts
Division of the Middle Parts
2 Middle Parts
Step 3
Step 2
Step 1
Step 0
N
At the end of data traversal,
data is divided into 2 end
p
arts and 32 middle
p
arts.
Target Boundaries
Source Boundaries
A METHOD FOR 3D MORPHING USING SLICES
295
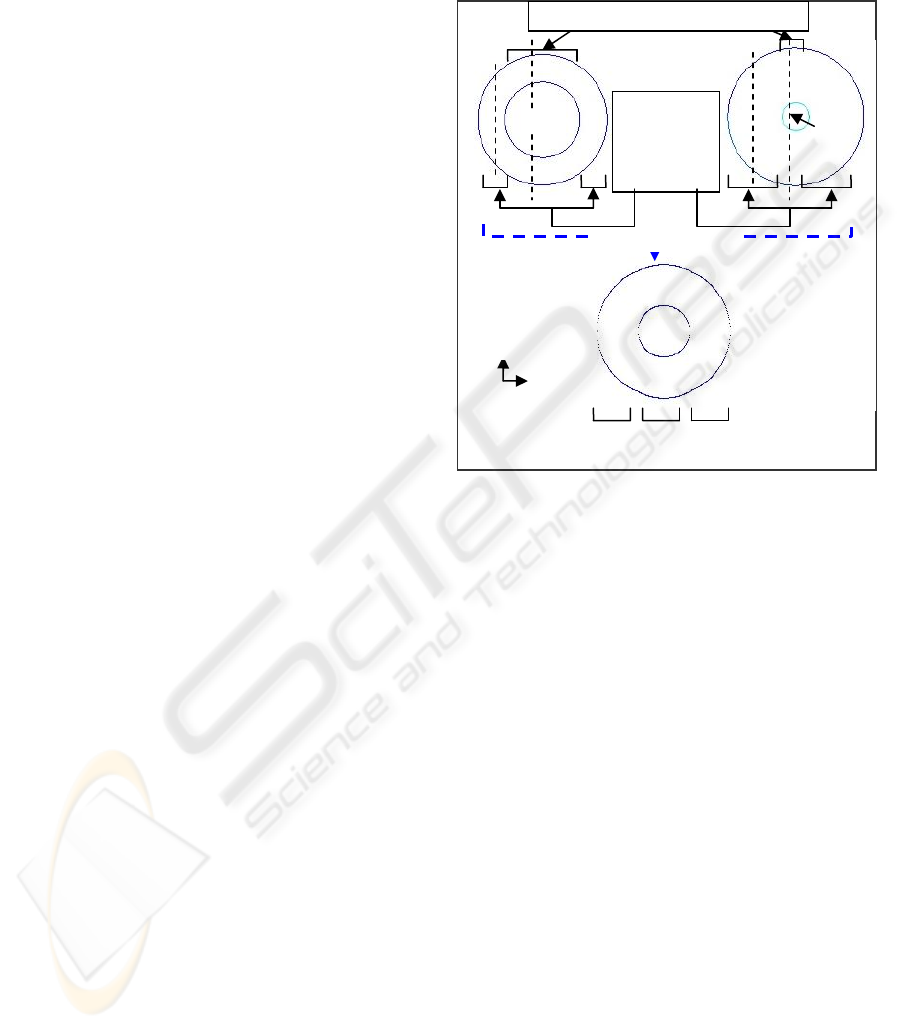
(X
max
) with a traversal plane defined as (1,0,0). For
each source and target boundaries, traversal spacings
are determined separately. Equal number of
traversals is performed for both source and target
data. Traversal spacing is determined as follows:
Spacing = (X
max
– X
min
)/ Number of Traversals
Source and target boundary points are extracted
from the traversals. If the number of extracted points
in any cut plane happens to be odd, it is made to be
even. Next interpolation is performed onto the XZ
plane. For simplicity linear interpolation is used in
our implementation. Here it should be noted that
only one normal is extracted per boundary regardless
of whether any particular boundary consists of
multiple holes or empty spaces. Also each boundary
has one center irrespective of the irregular geometric
configuration of that particular boundary.
Three special cases need to be considered during
interpolation. They are as follows:
Case 1: Both Source and Target Boundaries
Contain no Empty Spaces.
Source points are just
interpolated with target points. Enhancement of the
interpolation process can be carried out when both
source and target have equal number of regions and
there are more than one region in both. Region is an
area where the number of points extracted by the cut
plane is the same while traversing along the X axis.
In Figure 5, both source and target boundaries
consist of equal number of regions i.e. 3 (two 2-
point region and one 4-point region). Hence the
interpolated point clouds also have three regions.
Case 2: Only One of the Source and Target
Boundaries Contains Empty Spaces. The number
of empty spaces is calculated for the boundary
which contains empty spaces. Then equal number of
empty spaces are inserted into the other boundary so
that empty space will appear in the interpolated
point clouds.
Case 3: Both Source and Target Boundaries
Contain Empty Space. When there are equal
number of empty spaces in both source and target
boundaries, we have equal number of regions. Thus
corresponding regions from both source and target
can be interpolated. However when there are
unequal number of empty spaces/ regions, rightward
and leftward traversals are carried out until either
one of source or target is exhausted (Figure 6).
Corresponding regions during the traver -sal are just
mapped and interpolated while the remaining
regions can just be mapped if the exhausted side
ends with an empty space. Otherwise a process
similar to Case 2 above is applied by inserting into
the region of the exhausted side the same number of
empty spaces left in the non-exhausted side.
Figure 5: Interpolation of Points after Region Separation.
3.4 Orientation and Translation of
Interpolated Boundaries
Each of the interpolated boundary already projected
onto the XZ plane is oriented along the resultant
normal of each of the source and target boundaries
and translated to the average center of each of source
and target boundaries (Figure 7). When all the
interpolated boundaries are oriented as well as
translated, we get the outline of the morphed output.
Figure 8 describes this sequence.
3.5 Surface Reconstruction
From the stack of oriented and translated bounda -
ries, surface of the morphed object is constructed.
Each of the boundaries merges with the next boun-
dary by dividing the in-between space of the two
consecutive boundaries into a number of cells and
each cell is connected to its neighboring cells. Sur -
face construction is performed by only considering
each of the two consecutive boundaries.
2-pt Region (At an
y
particular distance
along X, number o
f
intersected points
by a plane (1,0,0), is
2)
x
Interpolated Point Clouds
(
0
,
0
,
0
)
(0,0,0)
4-point Region (At any particular distance along X,
number of intersected points by a plane (1,0,0), is 4).
SOURCE TARGET
(
0
,
0
,
0
)
z
2-point
Re
g
ion
4-point
Region
2-point
Region
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
296

Rightward Traversal Leftward Traversal
Figure 6: Interpolation case when there are unequal number of empty spaces between source and target.
Figure 7: Orientation and Translation of a Single
Interpolated Boundary.
Figure 8: Orientation and Translation of All Interpolated
Boundaries.
This simplifies the overall surface reconstruction
process as where data is highly irregular, necessary
modification among cell coordinates is limited to
only two consecutive boundaries. Surface
reconstruction in detail is discussed next.
3.5.1 Separating Disconnected Region
Each consecutive boundary may have regions which
are disconnected from one another (Figure 9(a)).
Nearest neighbor searching is carried out to find this
kind of regions. The disconnected regions are
horizontally mapped (for better effect) and the other
regions are to be vertically mapped (Figure 9(b)).
The details of the vertical mapping are discussed
in the next sub section.
Figure 9: Separating Disconnecting Regions between Two
Consecutive Boundaries.
3.5.2 Basic Cell Construction
After region separation, two consecutive point/ cell
arrays (representing two consecutive slices) are
obtained and vertically mapped. The two arrays
which contain the number of interpolated points at
each index need to be compressed so that the process
of mapping can be carried out in an easier and
straightforward manner.
Point clouds in top slice
with only one region
Point clouds in bottom slice
with two separate regions
Re
g
ion 1
Region 2
After region separation point clouds in
top slice vertically mapped with region 1
of bottom slice
Disconnected region 2
in bottom slice is
horizontally mapped
(a)
(b)
(0,0,0)
y
z
(0,0,0)
x
x
z
N1
C1
C2
N2
N = (N1 + N2)/2
C = (C1 + C2)/2
Source Slice
Tar
g
et Slice
Oriented and Inter
p
olated Slice
Re
g
ion1
Re
g
ion1 Re
g
ion3Re
g
ion2
Re
g
ion2
Re
g
ion4
Re
g
ion5 Re
g
ion6
Re
g
ion3
Region 1 of Source maps
with Re
g
ion 1 of Tar
g
et
Region 3 of Source maps
with Re
g
ion 6 of Tar
g
et
Re
g
ion 2 of Source ma
p
s with Re
g
ion 2 …. Re
g
ion 5 of Tar
g
et
Interpolated Points
z
x
(c)
A METHOD FOR 3D MORPHING USING SLICES
297
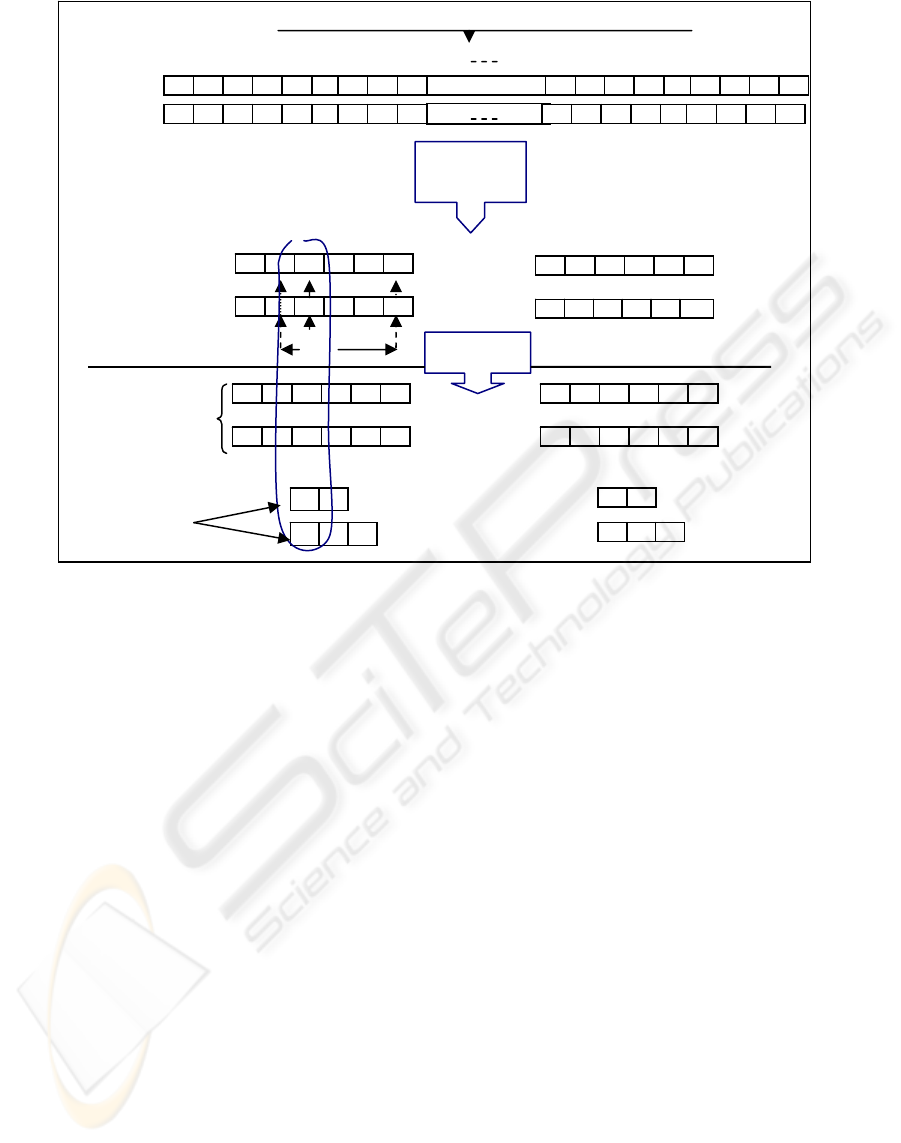
Two Arrays Containing the Number of Interpolated Points
0 1 2 3 4 5 6 7 8 9 40 41 42 43 44 45 46 47 48 49
Index No:
Figure 10: Basic Cell Construction between Two Consecutive Interpolated Boundaries.
Figure 10 shows the process of compressing two
consecutive arrays. In the compression, the arrays
are transformed into two new arrays each: region
number array (where region numbers are stored) and
number of occurrences array (where the number of
occurrences of each region number are stored).
Firstly, the size of both arrays should be made equal
using a heuristic approach. Sometimes some index
values are dissolved and some are omitted in order
to make the size of both arrays equal. Corresponding
values of the number of occurrences arrays should
also be made equal so that they are ready to be
vertically mapped. In the case of unequal values, the
larger of the two values is made equal to the smaller
number by removing excess number of that
particular number of occurrences value.
Corresponding numbers in the two region number
arrays should also be equal for the purpose of
vertical mapping. If they are not equal, a further
processing needs to be done. The process starts with
finding the nearest matched index values of the
region number arrays by traversing to the left and
the right. The nearest matched values will ensure
better continuity between different-numbered
regions. Next the corresponding region numbers are
split into two portions where the values of the region
number of the first portion is derived from the
continuous mapping of the nearest matched index
values to the corresponding region number values
and the values of the region number of the second
portion are the remaining region numbers resulting
from the split.
In the example (Figure 10), the first
discrepancy occurs at index number ‘2’ and the
nearest matched values are at index number ‘1’ with
a value of ‘4’ and ‘4’. The current values (i.e. 8 and
6) need to be split into two portions. The first
portions are made equal to ‘4’ and the second
portions are assigned the remaining values (8-4 = 4
and 6-4 = 2).
At the end of the entire processing, two
sets of region number arrays are obtained. The top
set (Figure 10(a)) now consists of equal region
number and can therefore be vertically mapped
whereas each of the bottom set (Figure 10(b)) is to
be horizontally mapped separately. Enhancement is
carried out in surface reconstruction when empty
space is met or at the transition point between two
different-numbered regions.
1
st
Number Array
2
nd
Number Array
Index No:
1
st
Array
2
nd
Array
Each Array is
Compressed
to
2 Arrays
4 2
2 4 2
8
7
8
7
9
At the End of the
Entire Processing
2
2
2
2
2
2
2
2
4
4
---
4
4
4
4
4
4
4
4
4
4
2
2
2
2
2
2
2
4 6
2
4
4
4
4
4
4
4
4
4
4
Number of Occurrences Array
Region Number Array
0 1 2 3 4 5
0 1 2 3 4 5
8
9
8
7
9
9
8
9
8
7
9
9
2
4
8
6
4
4
2
4
6
8
6
4
2
4
4
4
4
4
2
4
4
4
4
4
8
9
8
7
9
Vertical Mapping
9
between
Corresponding Cells
8
9
8
7
9
9
Separate
Horizontal
Mapping
(
a
)
(
b
)
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
298

4 IMPLEMENTATION AND
RESULTS
The algorithm has been implemented using C++
with Visualization Tool Kit (VTK) as graphics plat -
form. In Figure 11(a), a sequence of three interme-
diate stages is generated using ‘5’ as the number of
steps with the initial direction of traversal for source
as well as target along the maximum direction of the
eigen vector i.e. ‘alignment = 0’. Using ‘4’ as the
number of steps, the same sequence is generated
without producing major distortion to the eye. As the
number of step increases, the number of slices is
doubled which also increases the overall run time.
Figure 11(b) shows the morphing sequence
between two tori each with different radius with the
initial direction of traversal along the minimum
direction of eigen vector i.e. ‘alignment = 2’ for both
source and target. In Figure 11(c), a morphing
sequence between a complex object and a bent pipe
has been generated. Here the initial direction of
traversal for the source is along the minimum direc-
tion of eigen vector i.e. ‘alignment = 2’ whereas the
initial direction of traversal for the target is along the
maximum direction of eigen vector i.e. ‘alignment =
0’. Figure 11(d) shows the morphing sequence
between a conic spiral and a torus with the initial
directions of traversal for both source and target
along the maximum direction of eigen vector i.e.
‘alignment = 0’.
Figure 11: Morphing Sequence between Source (left most)
and Target (right most) for Different Eigen Vectors as
Initial Direction of Traversal.
As highlighted in Section 3.1, the initial direction
of traversal can also be forced to happen along the
principal axis. In Figure 12(a), morphing sequence
between a teapot and a parametric surface ‘dini’ has
been generated. Here the initial directions of
traversal for both source and target are along the Y-
axis. Figure 12(b) shows the morphing sequence
between a cow and a cylindrical object. Here the
initial direction of traversal for the source is along
the X-axis and the initial direction of traversal for
the target is along the Y-axis.
(a)
(
b
)
Figure 12: Morphing Sequence between Source (left most)
and Target (right most) for Different Principal Axis as
Initial Direction of Traversal.
Figure 13 compares the gradual morphing
sequence between the same source and target as
used in Figure 11(a) when initial direction of tra -
versal for source/ target changes. Figure 13(a) shows
the gradual transformation between source and
target when the initial directions of traversal for
source and target are along medium and maximum
direction of the eigen vector i.e. ‘alignment = 1’ and
‘alignment = 0’ respectively. Figure 13(b) shows the
morphing sequence when the initial directions of
traversal for both source and target are along the
minimum direction of eigen vector i.e. ‘alignment =
2’.
Figure 13: Morphing Sequence between the Same Source
(left most) and Target (right most) for Different Eigen
Vectors as Initial Direction of Traversal.
(a)
(
b
)
(
a
)
(
b
)
(
c
)
(
d
)
A METHOD FOR 3D MORPHING USING SLICES
299

Instead of principal axis, if morphing sequence is
generated along the longitudinal direc -tion, warping
in rigid body is also considered when it is needed.
Figure 14 compares this situation. In Figure 14(a),
the morphing sequence is generated with initial
direction of traversal along the principal axis X and
Y for source and target respectively whereas in
Figure 14(b), the morphing sequence is generated
with the initial direction of traversal for both source
and target along the maximum direction of eigen
vector i.e. ‘alignment = 0’.
Figure 14: Morphing Sequence between the Same Source
(leftmost) and Target (rightmost) with (a) Principal Axis
and (b) Eigen Vector as Initial Direction of Traversal.
5 DISCUSSION
This section compares the proposed algorithm with
some other existing morphing algorithms on the
basis of a number of criteria for good morphing.
Most surface-based methods consider the
distortion/rotation of the rigid body, but division of
both source/ target into a number of morphing
patches or meshes is needed at the expense of a large
number of user input and longer pre-processing
stage ((Kent, -1992), (Lazarous, 1994), (Gregory,
1998), (Breen, 2001)). The proposed algorithm
works without any user input with default initial
settings (‘number of steps = 4’ and ‘alignment =
max’). If variations in the number of steps and
alignments are desired, the user just needs to specify
these two variables. The number of slices can also
be reduced by varying the number of steps. This
automated method of reducing the number of slices
as well as run time is absent in the most other
algorithms. In most other existing algorithms,
specific number of user-defined disk fields (Chen,
1996) or point/line fields ((Kent, 1992), (Lazarous,
1994), (Gregory, 1998), (Breen, 2001)) are used.
Varying these fields involves a considerable amount
of user intervention and longer pre-processing time:
minor variation in these fields can generate a major
variation in the output. The proposed algorithm
automatically traverses the data along its alignment
and is free from any inaccurate user intervention and
at the same time if needed allows user to specify the
initial direction of traversal.
Simplicity is one of the major characteristics of
the proposed algorithm. Some early surface-based
algorithm preserves this feature but at the same time
fails when the object is a bit complex producing self-
intersecting intermediate objects (Hong, 1988). In
the proposed algorithm, aligned slices are extracted
from data traversal and before interpolation, slices of
the corresponding source and target slices are
projected onto the XZ plane. Hence chances of self-
intersection are very slim as that can happen when
triangulated surfaces are interpolated or extracted
slices are not properly aligned.
(a)
Another important feature of a good morphing is
that intermediate outputs should be confined to the
geometric features of source and target only.
However sometimes unnecessary fea -tures are also
seen among the intermediate morphed objects
((Gregory, 1998), (Kent, 1992)). In the pro -posed
algorithm smooth transition takes place bet -ween
source and target. Orientation as well as rota -tion of
a rigid body are preserved while morphing .
(
b
)
Some volume-based methods use discrete
mathematical function in morphing between
complex objects ((Hughes, 92), (He, 1994), (Turk,
1999)) generating smooth output using sophisticated
interpolation technique. But interpolation is only one
facet of morphing. The major shortcoming of these
methods is that they overlook the curvature of rigid
body while morphing, which is one of the most
important properties needed to be considered for
morphing between curved objects. The proposed
algorithm nicely fills in the gap. Some volume-based
algorithms alleviate this problems ((Payne, 1992),
(Breen, 2001)). However they are highly sensitive to
the user-specified initial overlapping of source and
target. These methods have weakness around the
regions of high curvature: accuracy of intermediate
objects also depends on the accuracy of user-defined
overlapping of source and target. This sometimes
results in incomplete morphed output in case of
curved objects. The proposed algorithm shows more
consistency than these methods.
In the proposed algorithm, instead of traversing
along the longitudinal direction of data, traversal can
also take place along any particular direction
producing different morphing sequences. This
flexibility may be difficult to achieve in surface-
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
300

based algorithms or in some volume-based
algorithms which exhibit characteristics like surface-
based algorithms (Lerois, 1995). Some volume-
based algorithms can consider this but may involve
considerable user intervention ((Payne, 1992),
(Chen, 1996), (Breen, 2001)). Morphing involving
discrete mathematical functions for interpolation
((Hughes, 1992), (He, 1994), (Turk, 1999)) is
capable of traversing along only a specified
direction.
Now let us analyze the algorithm in terms of
efficiency. In field morphing, control data sets are
used to specify coordinate mapping hence time
complexity is usually Ө(nm) as all coordinates of a
single dataset are more or less influenced by all
control fields (Chen, 1995). Here ‘n’ is the size of
volume and ‘m’ is the number of control fields. In
the proposed method, control fields i.e. slices are
automatically determined during data traversal and
these control fields have little influence or control in
coordinate mapping: only coordinates of respective
boundaries are influenced. Hence if the number of
extracted coordinates from each boundary is ‘p’ and
the number of automatically defined slices (‘m’) are
considered as control fields, then time complexity is
Ө(mp + m). Here ‘mp’ can be equated with the
volume size ‘n’ hence time complexity for the
proposed algorithm is Ө(n + m) which is much less
than volume morphing using disk field Ө(nm)
(Chen, 1996).
6 CONCLUSIONS
Simplicity and flexibility are two major characteris -
tics of the proposed algorithm which have made it
more dynamic and extendible than other existing
morphing algorithms. Future work includes exten -
ding the algorithm in order to show the extendibility
of the method by incorporating influence shape
while morphing including multiple influences and
exploitation of the method in parallel/distributed
computing environment as simple data structure of
sliced body and binary subdivision is suitable for
both data as well as functional partitioning.
REFERENCES
Hong, T., Magnenat-Thalmann, N., Thalmann, D., 1988.
A General Algorithm for 3D Shape Interpolation in a
Facet-based Representation. In Proceedings on Gra -
phics Interface `88, pages 229-235.
Hughes, J., F., 1992. Scheduled Fourier Volume
Morphing, ACM SIGGRAPH Computer Graphics:
26(2): 43-46.
Payne, B., Toga, A., 1992. Distance Field Manipulation
of Surface Models , IEEE Computer Graphics and
Applications: 12(1), 65-71.
Kent, R., J., Carlson, W., E., Parent, R., E., 1992. Shape
Transformation for Polyhedral Objects, In Procee
dings of ACM SIGGRAPH’99, pages 335-342.
Kaul, A., Rossignac., J., 1992. Solid Interpolationg Defor -
mations: Construction and Animation of PIPS,
Computers and Graphics: 16(1), 107-115.
Lazarous, F., Lopes, Verroust, A., 1994. Feature based
Shape Transformation for Polyhedral Objects, In Fifth
Eurographics Workshop on Animation and
Simulation, pages 241-254.
He, T., Wang, S., Kauffman, A., 1994. Wavelet-based
Volume Morphing, In Proceedings of IEEE
Visualization, page 85-92.
Lerois, A., Garfinkle, C., D., Levoy, M., 1995. Feature-
based Volume Metamorphosis, Computer Geaphics
29, “Annual Conference Series”, pages 449-456.
Chen, M., Jones, M., W., Townsend, P. 1995. Methods for
Volume Morphosis, In Image Processing and
Broadcast for Video Production, Y. Parker and S.
Wilbur (eds), Springer-Verlag, Berlin, pages 280-292.
Chen, M., Jones, M., W., Townsend, P., 1996. Volume
Distortion and Morphing Using Disk Fields,
Computers and Graphics: 24(2), 567-575.
Gottschalk, S., Lin, M., C., Manocha, D., 1996. Obbtree:
A Hierarchical Structure for Rapid Interference
Detection, Computers and Graphics (30), “Annual
Conference Series”, pages 171-180.
Gregory, A., State, A., Lin, M., C., Manocha, D.,
LivingSton, M.,1998. Feature-based Surface Decom-
position for Correspondence and Morphing between
Polyhedra, In Computer Animation and Procee
dings’98, pages 64-71.
Lee, A., W., F., Dobkin, D., Sweldens, W., Schrőder, P.,
1999. Multiresolution Mesh Morphing, In Proceedings
of SIGGRAPH’99, pages 343-350.
Turk, G., O’Brien, J., F., 1999. Shape Transformation
using Variational Implicit Functions, In Proceedings
of ACM SIGGRAPH’99, pages 335-342.
Breen, D., E., Whitaker, R., T., 2001. A Level Set
Approach for the Metamorphosis of Solid Models,
IEEE Transactions on Visualization and Computer
Graphics: 7(2), 173-192.
A METHOD FOR 3D MORPHING USING SLICES
301
