
VOXEL OCCUPANCY WITH VIEWING LINE INCONSISTENCY
ANALYSIS AND SPATIAL REGULARIZATION
Marcel Alcoverro and Montse Pard
`
as
Image and Video Processing Group, Technical University of Catalonia (UPC)
Jordi Girona, 1-3, 08034 Barcelona, Spain
Keywords:
Visual hull reconstruction, Inconsistencies, Graph cuts, Shape from silhouette.
Abstract:
In this paper we review the main techniques for volume reconstruction from a set of views using Shape from
Silhouette techniques and we propose a new method that adapts the inconsistencies analysis shown in (Land-
abaso et al., 2008) to the graph cuts framework (Snow et al., 2000) which allows the introduction of spatial
regularization. For this aim we use a new viewing line based inconsistency analysis within a probabilistic
framework. Our method adds robustness to errors by projecting back to the views the volume occupancy ob-
tained from 2D foreground detections intersection, and analysing this projection. The final voxel occupancy of
the scene is set following a maximum a posteriori (MAP) estimate. We have evaluated a sample of techniques
and the new method proposed to have an objective measure of the robustness to errors in real environments.
1 INTRODUCTION
Shape reconstruction from a set of cameras is rel-
evant for a wide range of applications in computer
vision. A detailed understanding of 3D scenes vi-
sual content for tasks as navigation, object manipu-
lation, visual recognition or tracking, requires a ex-
plicit 3D model of the environment and the objects
in the scene. The external surface of opaque objects
can be reconstructed with more or less precision de-
pending on the information available from the multi-
ple views. Given a set of silhouettes of an object S
in the scene, the visual hull is the maximal volume
which is silhouette-equivalent to S , i.e, which can
be substituted for S without affecting any silhouette
(Laurentini, 1994). The set of silhouettes is consid-
ered to be consistent when there exists at least one
volume which completly explains them. Most of the
reconstruction techniques consist in computing the vi-
sual hull of the scene.
Visual hull reconstruction has different drawbacks
depending on the format of the 3D representation
(voxels, surfaces, polyhedral), or the nature of the
data (synthetic, real). Focusing on the format of repre-
sentation, voxel-based approaches suffer from quan-
tization artifacts and also of a high memory cost.
Surface-based approaches (Franco and Boyer, 2003)
and image-based approaches (Matusik et al., 2000;
Casas and Salvador, 2006) solve this problem but
may have a higher computational cost. Other ap-
proaches are more focused in the treatment of real
data, where errors appear due to the capturing pro-
cess and the silhouette extraction process, which are
not present in synthetic data (Landabaso et al., 2008;
Snow et al., 2000; Franco and Boyer, 2005; Land-
abaso and Pard
`
as, 2006). Robustness to these errors
is added by analysing the redundancy of information
available from the views.
In this paper we present an approach for voxel
based visual hull reconstruction, where an analysis
of inconsistencies provides robustness to errors due
to occlusions and missing parts in silhouette extrac-
tion, and a global estimation of the voxel occupancy
allows to introduce spatial regularization. This spatial
regularization allows a smoothing of the visual hull,
improving its quality.
We first present a review of visual hull reconstruc-
tion algorithms in section 2. Then we formulate the
problem of the voxel occupancy estimation consider-
ing inconsistencies and regularization in section 3.
2 REVIEW OF VISUAL HULL
RECONSTRUCTION
ALGORITHMS
Uniform Voxel-based Visual Hull. Regular vox-
elization based techniques represent the space with a
regular grid of elementary volumes (voxels). Scene
464
Alcoverro M. and Pardàs M. (2009).
VOXEL OCCUPANCY WITH VIEWING LINE INCONSISTENCY ANALYSIS AND SPATIAL REGULARIZATION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 464-469
DOI: 10.5220/0001786804640469
Copyright
c
SciTePress

representation usually consists in individual voxel
classification into a finite set of labels which define
voxel occupancy.
Shape from Silhouette (SfS) techniques project
each voxel into all the views. As a voxel projects into
several pixels a function called projection test deter-
mines whether the voxel view is considered within the
silhouette or not. These techniques usually need fore-
ground object silhouettes previously computed for all
views. Voxel size is a fundamental parameter. It de-
termines the balance beetween reconstruction preci-
sion and computational charge, and should be tuned
depending on the application.
Voxel-based methods suffer from quantization and
aliasing errors. Each voxel, once projected onto cam-
era images, leads into a irregular amount of data, as
the number of pixels to analyse depends on its dis-
tance to the camera and the camera distorsion.
Multi-resolution Techniques. An efficient strategy
to compute the visual hull is by representing the ob-
ject with an octree (Szeliski, 1993). The volume is
represented by a tree which allows a hierarchical re-
finement of the model. Such tree is formed by subdi-
viding cubes recursively, which provides lower com-
putational cost in zones where there is no surface,
while the model precison can be incremented.
Polyhedral Visual Hull. Several approaches (Ma-
tusik et al., 2000), (Casas and Salvador, 2006), re-
construct the visual hull based in 3D constructive
solid geometry intersections. Silhouettes are back-
projected creating a set of extruded cones, which are
then intersected to form a polyhedral visual hull.
In such techniques geometry computation is done
in the image space to avoid the effects of a sampling
in the 3D space. This allows a maximum precision in
the 3D space but demands high computation.
The approach in (Casas and Salvador, 2006) pro-
poses a 3D geometry for multi-view analysis based
on irregular elemental volumes conexels. The geom-
etry of the conexels is not regular in the 3D space but
once it is projected, it becomes a regular image re-
gion. This allows to adapt 3D sampling parameters
to image resolution parameters, so multi-view scene
analysis is centered in the 2D space where we have
the direct data.
Reconstruction with Noisy Silhouettes. The Vi-
sual Hull reconstruction methods described above
are designed considering that silhouettes are error-
free. In real world scenarios silhouettes contain errors
introduced by 2D foreground detection algorithms,
camera calibration errors and image capturing noise.
In such situations the previous techniques obtain the
part of the volume which projects in a consistent man-
ner in all the silhouettes.
A projection test relaxation takes benefit from
multi-view redundancy to improve the robustness to
noisy silhouettes. An efficient and robust to errors
projection test is the sampling projection test (SPOT)
(Cheung, 2003). This method checks R pixels in the
splat of a voxel. The test is passed if at least N out of
the R pixels belong to the silhouette.
Another approach consists in classifying voxels
as occupied or empty using multi-view information
without using previously computed foreground sil-
houettes (Snow et al., 2000). An energy function is
defined for the scene, such that its minimization will
determine the state of each voxel. A data term and a
regularization term are involved. The data term is a
function of the intensity observed for each voxel pro-
jection into the views. The regularization term intro-
duces a spatial smoothing property. Such function can
be efficiently minimized using graph cuts. This tech-
nique avoids 2D foreground detection errors by post-
poning the foreground classification to the last step,
when multi-view information is available.
Also oriented to use cooperatively the multi-view
information is the work presented in (Franco and
Boyer, 2005).
Reconstruction with Silhouette Systematic Errors.
A second kind of errors are systematic errors caused
by occlusions or failures in the 2D foreground detec-
tion technique. Common errors in foreground detec-
tion algorithms are, for instance, when active objects
have the same color than the corresponding back-
ground. In such situations a miss of foreground de-
tection in a camera will propagate into the 3D space
causing a miss of reconstruction in large parts of the
volume. Another common error cause occurs when a
static background object occludes a part of an active
object from a certain view, producing also a miss of
part of the volume.
The algorithm Shape from Inconsistent Silhouette
(SfIS) (Landabaso et al., 2008) corrects this kind of
errors by using the inconsistencies produced between
the projection of the shape reconstructed by a stan-
dard Shape from Silhouette and the silhouettes de-
tected by the foreground detection algorithm.
VOXEL OCCUPANCY WITH VIEWING LINE INCONSISTENCY ANALYSIS AND SPATIAL REGULARIZATION
465

3 MAP-MRF RECONSTRUCTION
ALGORITHM
We consider the problem of active object volumetric
reconstruction from a set of images in a multi-camera
environment. We adopt a voxel-based approach, mod-
elling the 3D space with an occupancy grid G. Con-
sider {g
x
} = g
1
, . . . , g
n
, with n the number of voxels,
a set of binary variables g
x
∈ {0, 1}, where 1 means
the voxel in position x is occupied, while 0 means the
voxel is empty. Our aproach estimates the state of G
given a set of images I = {I
1
, . . . , I
c
} with c the num-
ber of cameras.
A major problem in voxel-based reconstruction
procedures is to deal with the dependencies between
the observation space, the images from a set of cam-
eras, and the state space we are estimating, the voxel
grid. The state of a variable g
x
depends on the obser-
vations in the cameras; we thus consider a projection
function ξ
i
: G → p, which obtains a set of pixels re-
sulting from the voxel projection into camera i. The
state of g
x
will depend on the observations in all pixels
p ∈ ξ
i
(g
x
). Moreover, we should take into account the
dependences between variables that are in the same
viewing line from a given camera. Consider a view-
ing line of a voxel g as a set of voxels {L
i
} ⊂ G for
which their projection has non null intersection with
ξ
i
(g). Variables in L
i
will have interdependences.
Classical algorithms assume independence be-
tween voxels, and each voxel state depends only
on observation of its projection. This confers more
tractability in a bayesian inference framework. But
true shape rather consists of large compact shapes
than isolated points. Similarly to (Snow et al., 2000),
we make the voxel description dependent of its neigh-
bours. We model the 3D scene by a locally depen-
dent Markov random field (MRF). This property is
appropiate for the global estimation of the grid state
in smart rooms or similar environments. This model
assumes a dependence between each voxel and its
neighbourhood, thus we should take care with the de-
pendences between voxels.
Our algorithm is divided into two steps. Dur-
ing the first step we take the viewing line into ac-
count in order to deal with inconsistencies, occlu-
sions, projection errors and image foreground detec-
tion errors. In this step we will consider voxel statis-
tical independence to infer a voxel occupancy proba-
bility P(g
x
= 1| I). In the following sections we will
refer to the occupancy probabilities for each voxel as
P
1
, . . . , P
x
, . . . , P
n
. Step 1 is inspired by (Landabaso
et al., 2008).
Dependencies between voxels are dealt during the
second step. We perform a global occupancy estima-
tion of the grid G, with P
x
given for each voxel, and
considering G as a locally dependent MRF. Step 2 is
inspired by (Snow et al., 2000).
3.1 Visual Hull Occupancy Probability
Inference
In reconstruction methods based on silhouette inter-
section, a foreground detection miss in any of the
cameras will cause voxel occupancy errors in all vox-
els in the viewing line of such miss. In order to im-
prove that error propagation, we propose to postpone
the foreground decision to a later step, in order to use
all the cameras information for the voxel occupancy
decision.
A probabilistic framework for foreground detec-
tion is needed. We use a bayesian estimation for
the foreground probability of a pixel, as presented
in (Landabaso and Pard
`
as, 2006), where each back-
ground pixel value is modelled as a unique gaussian
learned during a training period, and the foreground
pixel values are modelled as a uniform distribution.
We denote by P(φ|I
i
(p)) the foreground probability
of a pixel p in an image I
i
, where φ denotes the fore-
ground state for the pixel.
In our framework we should consider a probabilis-
tic projection test according to the foreground proba-
bilities in the view. We proceed, for instance, with the
simplest projection test, that considers only the pro-
jection of the center of the voxel, and decide upon
the pixel resulting from the projection. We name
ψ : G → r
i
the function which projects the center of
a voxel.
Then, in our case we have the one pixel projection
probability function opp such that for a certain camera
i and voxel x we obtain
opp
i
(x) = P(φ|I
i
(p)) (1)
where p = ψ
i
(x) is the pixel where the center of the
voxel projects in camera i.
A first approach to voxel occupancy probability
can be determined using the probability of a voxel x to
belong to the Visual Hull (VH), P(x ∈ VH) = P
V H
(x).
Considering the opp function we model P
V H
(x) as
P
V H
(x) =
i=c
∏
i=1
opp
i
(x) (2)
where a high voxel occupancy demands a high fore-
ground probability in all cameras.
Systematic errors contribute significantly to VH
errors, as described in section 2. To improve the voxel
occupancy probability model we add a term to deal
with this errors based on Shape from Inconsistent Sil-
houette (SfIS) technique (Landabaso et al., 2008).
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
466
BACK
INC
VH
IV
camera 1
camera 2
camera 3
camera 4
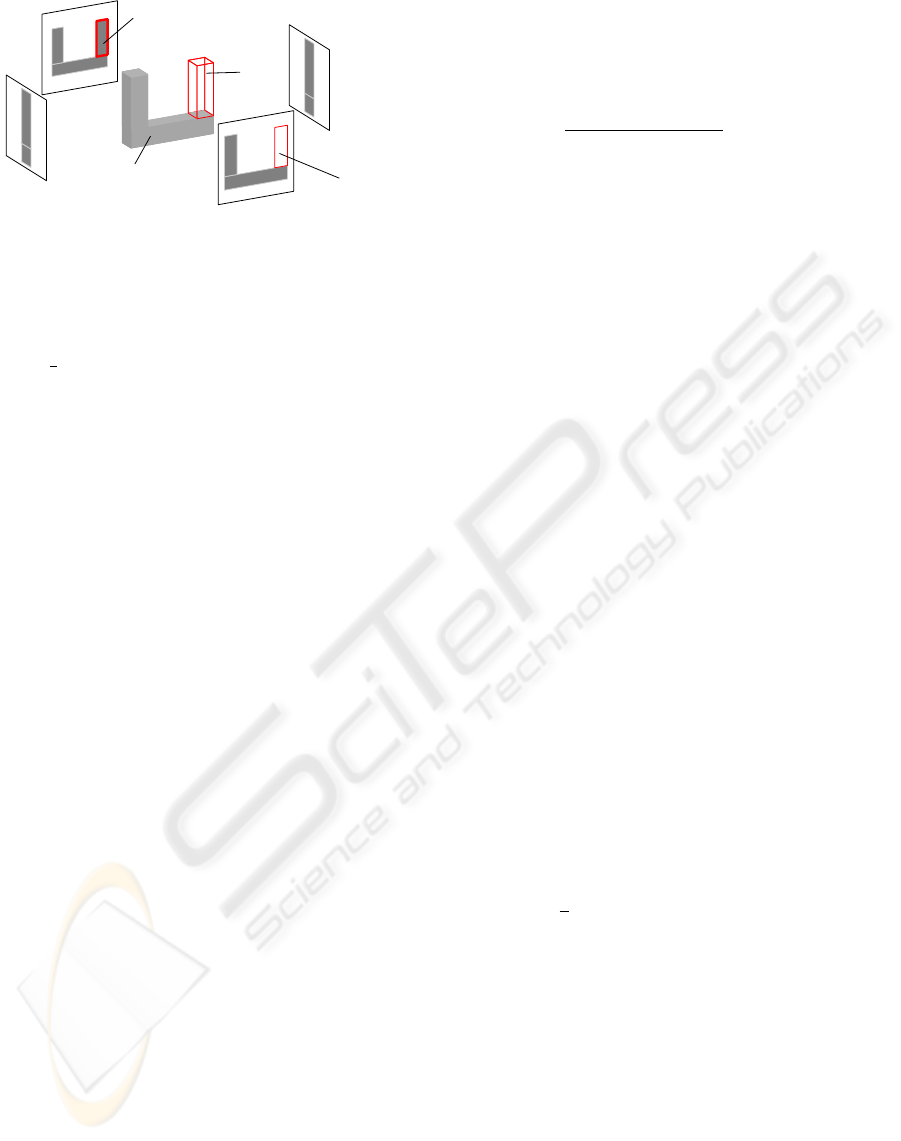
Figure 1: Example of the inconsistencies analysis. In each
camera we show the foreground silhouettes detected in gray.
We show in gray the volume obtained by silhouette intersec-
tion VH. IV is the inconsistent volume. IV projection into
camera 1 counts as BACK, while the projection in camera
3 counts as INC. In this case, the probability of IV to be
shape is
1
2
. Cameras 2 and 4 do not affect to this probability
as they do not provide useful information.
In (Landabaso et al., 2008) the geometric concept of
Inconsistent Volume IV is introduced as the volume
where does not exist a shape of the VH which could
possibly explain the observed silhouettes. The IV
contains the volumetric points that, in terms of consis-
tency, are candidates of not being classified as shape
by error.
We propose a new viewing line based inconsis-
tency analysis, used to model the probability of a
voxel of the IV to be shape, P(g
x
= 1|x ∈ IV), de-
noted in the following as P
IV
(x). Such technique is
suitable in a probabilistic framework in contrast with
the silhouette based technique introduced in (Land-
abaso et al., 2008).
We set the visual hull projection Ω
i
for a camera i,
an image such that each pixel p ∈ Ω
i
is the maximum
P
V H
of the voxels in the pixel viewing line,
Ω
i
(p) = max(P
V H
(x)) ∀ x ∈ L
i
(p) (3)
We define the inconsistency count for a voxel x as
INC(x) =
c
∑
i=1
P
φ|I
i
(ψ
i
(x))
1 − Ω
i
(ψ
i
(x))
(4)
which accounts for cases where the voxel does not be-
long to the VH, but it projects into a camera as fore-
ground.
We define also the background count for a voxel
as
BACK(x) =
c
∑
i=1
1−P
φ|I
i
(ψ
i
(x))
1−Ω
i
(ψ
i
(x))
(5)
which accounts for cases where the voxel does not
belong to the VH and its projection into a camera is
background. In cases where the inconsistencies count
is greater than the background count, it is more proba-
ble that the voxel has not a high occupancy probability
by error (Figure 1). Thus we set
P
IV
(x) =
INC(x)
INC(x) + BACK(x)
(1 − P
V H
(x)) (6)
Finally, the voxel occupancy probability resulting
from the first step inference is for each voxel x
P
x
= P
V H
(x) + P
IV
(x) (7)
These variables for each voxel serve as input for the
global estimation described in the following sections.
3.2 MAP-MRF Model
Once P
x
is inferred for each voxel from the data avail-
able in the views, as explained in section 3.1, we want
to estimate the global state of the grid G, denoted
by g. We set a conditional density function for each
voxel f (y
x
|g
x
= 1) = P
x
and f (y
x
|g
x
= 0) = 1 − P
x
.
The variables y = y
1
, . . . , y
n
are considered the ob-
servations for each voxel and are conditionally inde-
pendent. Then, according to Maximum a Posteriori
(MAP) estimation, the state g is chosen to maximize
the probability
P(g|y) ∝ l(y|g)P(g) (8)
where l(y|g) is the likelihood function, and P(g) a
prior distribution for g. As the variables y are inde-
pendent the likelihood function may be written,
l(y|g) =
n
∏
x=1
f (y
x
|g
x
). (9)
The prior distribution P(g) is modelled as a pairwise
interaction MRF of the form
P(g) ∝ exp[
1
2
n
∑
x=1
n
∑
x0=1
λ
xx0
(g
x
g
x0
+ (1 − g
x
)(1 − g
x0
)}]
(10)
with λ
xx
= 0 and λ
xx0
> 0. x and x0 are neighbours.
Consider ln{P(g|y)}. The state of G that maximizes
such function is also the MAP estimation of the voxel
occupancy. As presented in (Greig et al., 1989),
a graph might be build such that finding the mini-
mum cut in the graph is equivalent to maximizing
ln{P(g|y)}. Finding the minimum cut is a well known
problem which can be efficiently solved (Boykov and
Kolmogorov, 2004).
In order to have a more flexible use of the method,
we need some parameters to adjust the reconstruc-
tion behavior to different situations. We reformulate
the function to optimize as a global energy function,
VOXEL OCCUPANCY WITH VIEWING LINE INCONSISTENCY ANALYSIS AND SPATIAL REGULARIZATION
467
which allows to balance the relevance of the incon-
sistency analysis and the smoothing in the global es-
timation. We split the probability P
x
in two terms, as
in equation 7. Then we introduce constant parameters
to balance the weight beetween function terms. The
energy function is
E(g) =
A
n
∑
x=1
g
x
(1 − P
V H
(x)) + (1 − g
x
)(P
V H
(x))
+
+W
n
∑
x=1
(1 − g
x
)(P
IV
(x)) +
+
1
2
n
∑
x=1
n
∑
x0=1
λ
xx0
(g
x
− g
x0
)
2
(11)
where we have a first term to account for penalties re-
lated to the VH occupancy probability, a second term
that introduces the inconsistency analysis, to improve
the robustness to systematic errors. And the third term
introduces the spatial regularization. For a fixed value
of A, the weight parameters W and λ allow to adjust
the response to inconsistencies and the smoothing as
needed. Formula 11 is very similar to the energy to be
minimized in (Snow et al., 2000) section 4.2, where
the inconsistency term has been added.
4 EXPERIMENTAL RESULTS
We have evaluated several of the algorithms briefly
described in section 2 and 3, in order to make a qual-
itative and quantitative comparison of reconstruction
techniques.
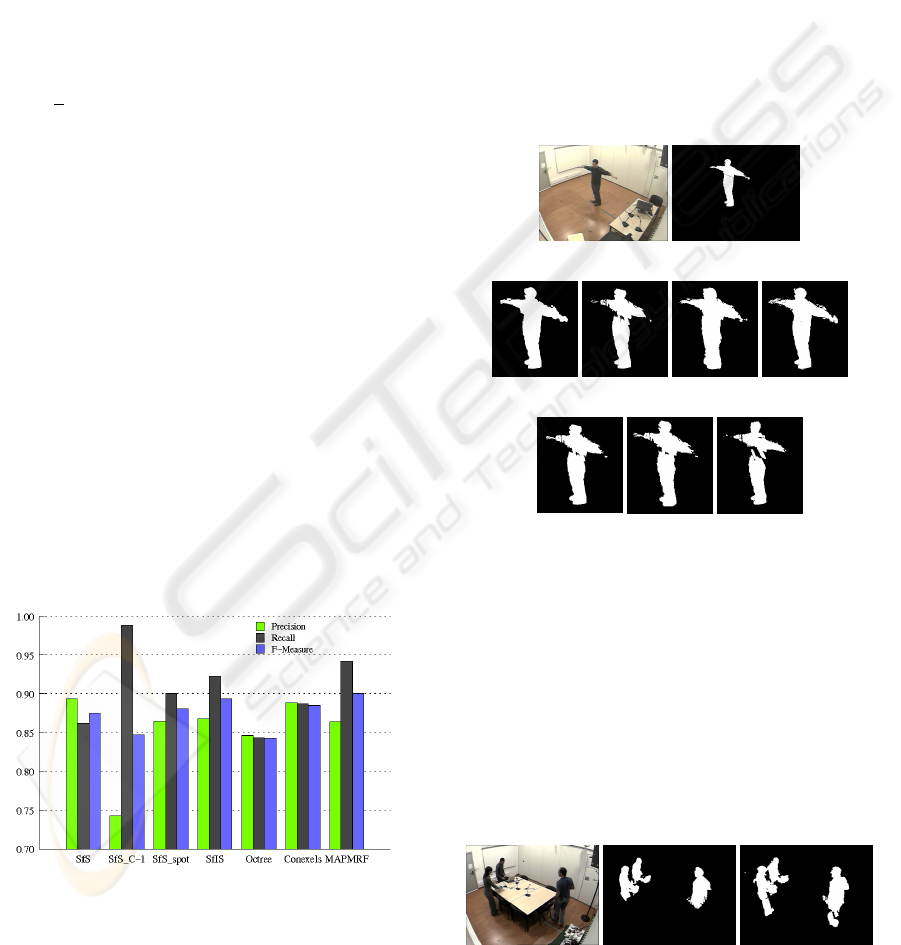
Figure 2: Results of the algorithms evaluation for 10
frames, 5 images per frame. SfS: SfS with one pixel projec-
tion test. SfS C-1: SfS considering 4 cameras intersection.
SfS spot: SfS with SPOT projection test. SfIS: P
FA
= 0.1,
P
Miss
= 0.2, P
φ3D
= 0.2, P
β3D
= 0.8. Octree: octree based
using distance transforms. Conexels: using a 3 × 3 pixels
quadrant. MAP-MRF: A = 50, W = 100, λ = 8.
To obtain quantitative results we used a real sequence
recorded with 5 cameras distributed around a smart-
room. The use of a real sequence allows a measure-
ment of the robustness to errors introduced by back-
ground substraction. Using real sequences has the
drawback that a volume ground truth is not available.
Thus, evaluation is performed by projecting the vol-
umes into the views and then comparing these pro-
jections with the image ground truth. Such condition
has limited the evaluation to 10 frames, which have
been segmented manually to obtain the ground truth.
For each view we processed the foreground silhou-
ettes in order to compare the methods with the same
input data. For the MAP-MRF method we used the
silhouettes as binary foreground probabilities.
(a) (b)
(c) (d) (e) (f)
(g)
(h) (i)
Figure 3: Results with 5 cameras. (a) original; (b) fore-
ground mask; (c) MAP MRF; (d) SfS; (e) SfS C-1. 4 cam-
eras intersection; (f) SfIS; (g) SfS with SPOT projection
test; (h) conexels; (i) octree reconstruction using distance
transforms.
We have employed the verification measures Preci-
sion, Recall and F-measure, commonly used in infor-
mation retrieval and also used in (Landabaso et al.,
2008). Figure 2 shows the results obtained. Figure 3
shows the projections of the volumes obtained for a
selected frame into one of the cameras.
(a) (b) (c)
Figure 4: Results with occlusions. (a) original; (b) SfS; (c)
MAP MRF.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
468

By analysing the results we can notice an inverse
relation between Precision and Recall in several of
the techniques. Considering certain tolerance to er-
rors in 2D foreground detection reduces losses in 3D
shapes. Even though, such tolerance introduces false
3D shapes as volumes are bigger. The case of SfS
with C − 1 intersections exemplifies this relation. As
detection only into 4 cameras suffices to classify a
voxel as shape, SfS C-1 algorithm is robust to 2D
foreground misses. This leads to a high Recall, but
the Precision is very poor, as shapes are much bigger.
Taking SfS as reference, SfS SPOT, SfIS and
MAP-MRF methods improve the Recall, as such
methods perform an error treatment. Results on Pre-
cision are worse for these methods than for SfS.
Conexels based method is better balanced. The
use of a multi-resolution approach, with a better treat-
ment of the projection task improves the Recall. Even
though, as there is no error treatement, systematic er-
rors from 2D silhouettes affects the result.
F-Measure gives a global quantitative result for
the methods. The MAP-MRF method has the high-
est value as it increases Recall with a limited decrease
of Precision. Note the improvement of the regular-
ization in the MAP-MRF method compared to SfIS
(figure 3.c, 3.f ). The resulting shape is more compact
and isolated voxels are removed. Such improvement
increases precision and lead to a better quality of the
shapes obtained.
In presence of occluders the MAP-MRF method
reconstruct parts of shape that classical SfS algo-
rithms do not reconstruct (figure 4).
5 CONCLUSIONS
We have evaluated several visual hull reconstruc-
tion algorithms, which solve the reconstruction prob-
lem focusing on different aspects: the voxel-based
approaches which deal with noisy silhouettes (SFS
SPOT, SFS C-1 ) and also with systematic errors
(SFIS) and techniques providing multi-resolution (oc-
tree, conexels), and polyhedral-based (conexels). We
have formulated a new voxel-based technique (MAP-
MRF) which provides robustness to noisy silhouettes
and systematic errors, and also provides a smoothing
property which improves the volumes obtained.
By the results obtained we conclude that the tech-
niques focused on robustness to errors reconstruct
parts of the shape that would be lost if no error treat-
ment was performed, but they also introduce false
shape detections. Such behavior may be interesting
for applications where it is relevant to reconstruct the
meaningful parts of the shape, and the non meaning-
ful false detections can be ignored. Furthermore the
technique MAP-MRF achieves the best global error
measurement.
ACKNOWLEDGEMENTS
This work has been partially supported by the Spanish
Administration agency CDTI, under project CENIT-
VISION 2007-1007.
REFERENCES
Boykov, Y. and Kolmogorov, V. (2004). An Experimen-
tal Comparison of Min-Cut/Max-Flow Algorithms for
Energy Minimization in Vision. IEEE Trans. PAMI.
Casas, J. and Salvador, J. (2006). Image-based multi-view
scene analysis using’conexels’. Proc. of the HCSNet
workshop on Use of vision in human-computer inter-
action, 56:19–28.
Cheung, K. M. G. (2003). Visual hull construction, align-
ment and refinement for human kinematic modeling,
motion tracking and rendering. PhD thesis, CMU,
Pittsburgh, PA, USA.
Franco, J. and Boyer, E. (2003). Exact Polyhedral Visual
Hulls. BMVC03, pages 329–338.
Franco, J. and Boyer, E. (2005). Fusion of Multi-View Sil-
houette Cues Using a Space Occupancy Grid. Proc. of
the 10th IEEE ICCV, 2:1747–1753.
Greig, D., Porteous, B., and Seheult, A. (1989). Exact max-
imum a posteriori estimation for binary images. Jour-
nal of the Royal Statistical Society, 51(2):271–279.
Landabaso, J. L. and Pard
`
as, M. (2006). Cooperative back-
ground modelling using multiple cameras towards hu-
man detection in smart-rooms. In Proc. EUSIPCO.
Landabaso, J. L., Pard
`
as, M., and Casas, J. R.
(2008). Shape from Inconsistent Silhouette. CVIU,
doi:10.1016/j.cviu.2008.02.006.
Laurentini, A. (1994). The Visual Hull Concept for
Silhouette-Based Image Understanding. IEEE Trans.
PAMI, 16(2):150–162.
Matusik, W., Buehler, C., Raskar, R., Gortler, S., and
McMillan, L. (2000). Image-based visual hulls. Proc.
of the 27th conf on Computer graphics and interactive
techniques, pages 369–374.
Snow, D., Viola, P., and Zabih, R. (2000). Exact voxel oc-
cupancy with graph cuts. Proc. IEEE CVPR, 1.
Szeliski, R. (1993). Rapid octree construction from image
sequences. CVGIP, 58(1):23–32.
VOXEL OCCUPANCY WITH VIEWING LINE INCONSISTENCY ANALYSIS AND SPATIAL REGULARIZATION
469
