
ROBUST FUZZY-C-MEANS FOR IMAGE SEGMENTATION
Moualhi Wafa and Ezzeddine Zagrouba
Equipe de Recherche Systèmes Intelligents en Imagerie et Vision Artificielle
Institut Supérieur d’Informatique, Abou Raihane Bayrouni, 2080, Tunisia
Keywords: Fuzzy-c-means clustering (FCM), Image segmentation, MR imaging, Spatial information.
Abstract: Fuzzy-c-means (FCM) algorithm is widely used for magnetic resonance (MR) image segmentation.
However, conventional FCM is sensitive to noise because it does not consider the spatial information in the
image. To overcome the above problem, an FCM algorithm with spatial information is presented in this
paper. The algorithm is realized by integrating spatial contextual information into the membership function
to make the method less sensitive to noise. The new spatial information term is defined as the summation of
the membership function in the neighborhood of pixel under consideration weighted by a parameter α to
control the neighborhood effect. This new method is applied to both synthetic images and MR data.
Experimental results show that the presented method is more robust to noise than the conventional FCM and
yields homogenous labeling.
1 INTRODUCTION
Magnetic resonance (MR) image segmentation is
often required for computer-aided diagnostic and
image analysis. Several approaches have been
investigated for automating this crucial and difficult
task in image processing (Leemput). The fuzzy-c-
means (FCM) clustering algorithm classifies pixels
with similar features into clusters and it has been
highly effective for MR image segmentation
(Chen(a), Yang, Bezdek(a), Lyer). Its success is due
to the introduction of fuzziness in the classification
process for image segmentation and the ability to
preserve more information from the original image.
However, conventional FCM takes care to pixels
features and does not consider their location or any
spatial information (Pham). Consequently, noisy
image influence badly the performance of the FCM.
Recently, many researchers try to incorporate spatial
information in the conventional FCM. Ahmed et al.
[Ahmed] modified the objective function of FCM to
allow the labeling of a pixel to be influenced by the
labels in its immediate neighborhood. The main
disadvantage of this method is the necessity to
compute the neighborhood term in each iteration
which is very time-consuming. To overcome this
problem, Chen and Zhang (Chen (b)) proposed two
algorithms based on the mean-filtered image and
median-filtered image which can be computed in
advance to replace the neighborhood term in the
above method. However, both methods can be
applied only for single feature. Shen et al. [Shen]
introduced two influential factors in segmentation
which are the difference between neighboring pixels
and their relative location in the image. In this paper,
we improve the conventional FCM by incorporating
spatial contextual information into the membership
function. The membership function of a pixel is
modified to consider the clusters distribution of its
immediate neighborhood weighted by a parameter α
to control the neighborhood effect. This scheme
aims to improve the effectiveness of the
conventional FCM to resist to noise. The rest of this
paper is organized as follows. In Section 2, the
conventional and the improved FCM are introduced.
The experimental results of the comparative study
are presented in Section 3. Finally, Section 4 gives
our conclusions and some issues for future work.
2 PROPOSED METHOD
In this section we introduce the principle of the
conventional FCM and the proposed FCM.
2.1 Conventional FCM
The Fuzzy-c-means (FCM) algorithm assigns pixels
87
Moualhi W. and Zagrouba E. (2009).
ROBUST FUZZY-C-MEANS FOR IMAGE SEGMENTATION.
In Proceedings of the First International Conference on Computer Imaging Theory and Applications, pages 87-91
DOI: 10.5220/0001787000870091
Copyright
c
SciTePress
to each cluster by using fuzzy memberships. Let X=
{x
i
, i=1,2…..,N| x
i
∈ R
d
} denote an image with N
pixels to be partitioned into c clusters, where x
i
represents feature data and d is its size. The
algorithm is an iterative optimization of the
objective function defined as follows (Bezdek(a)):
(1)
With the following constraints:
(2)
where
represents the membership of x
i
in the k
th
cluster,
is the k
th
class center,
denotes the
Euclidean norm, m>1 is a weighting exponent on
each fuzzy membership. The parameter m controls
the fuzziness of the resulting partition. The
membership functions and cluster centers are
updated by the following expressions:
(3)
and
(4)
The termination criterion is fixed as follows:
(5)
where V is a vector of cluster centers and is a
threshold that can be set by the user.
2.2 Improved FCM
Neighboring pixels in image has nearly similar
features. To incorporate this spatial information, a
spatial term is defined as:
(6)
where w
j
represents the set of neighbors located in a
n×n window centered on the pixel
. Therefore,
along all cases a 3×3 window was used throughout
this work. The parameter α is a tradeoff between
robustness to noise and preserving image details.
The spatial term
is incorporated into the
membership function as follows:
′
(7)
When a pixel belongs to the same cluster as the
majority of its neighbors, the spatial term just
fortifies its original membership. However, for noisy
pixel, each surrounding pixels try to pull it toward
its cluster and its weight is reduced by the labels of
its neigbhors. The improved FCM is robust to noise
and then denoted RFCM. The classification process
is a two-pass step in each iteration. The first step is
identical to the classification process in the
conventional FCM which computes the membership
function. In the second step, the spatial information
term is computed for each pixel by considering its
immediate neighbors weighted by a parameter α and
the original membership function is modified in the
objective function defined by equation (1).
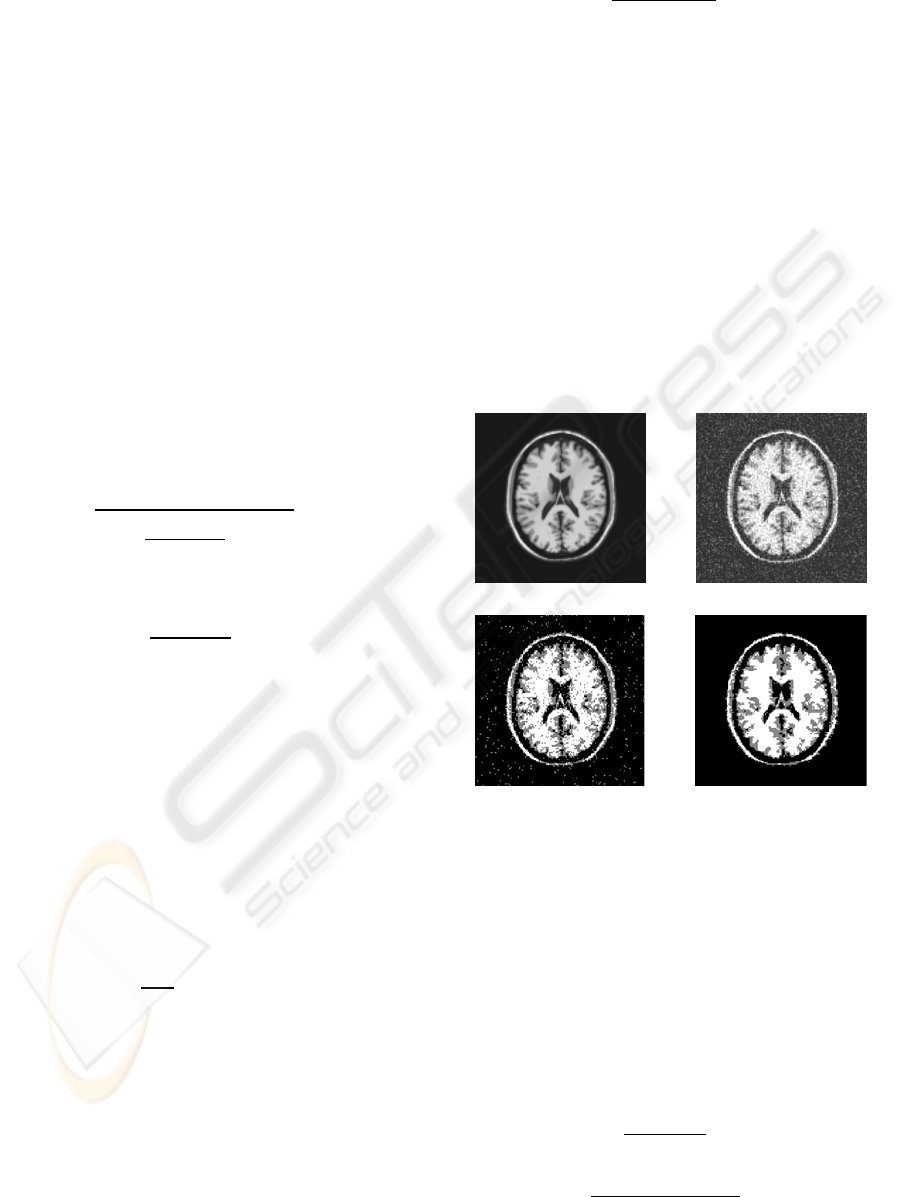
Figure 1: (a) MR T1 image (b) image with Gaussian noise.
Segmented image by (c) FCM; (d) RFCM (α=0.27).
The algorithm is stopped when the difference
between two cluster centers at two successive
iterations is less than a threshold (=2×10
-5
). To
quantitatively evaluate the performance of the
methods, we use two most known cluster validity
functions based on fuzzy partition. These two
validity functions are the partition coefficient V
pc
(Bezdek(b)) and the partition entropy V
pe
(Bezdek(c)). They are defined by:
(8)
(9)
(a)
(
b
)
(
d
) (c)
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
88

The idea of these validity functions is that the
partition with less fuzziness corresponds to better
performance. Thus, the best clustering is achieved
when the value V
pc
is maximal or V
pe
is minimal.
3 RESULTS AND DISCUSSION
In this section, segmentation results are illustrated
on digital MR phantoms and synthetic images. The
MR phantoms simulated the same features of the
T1-weighted MR image. The main advantage of
using digital phantoms to validate segmentation
methods is the prior knowledge of the images
characteristics and parameters such as noise or
others images artifacts (Goldszal). In all the
examples, α varies between 0.1 and 1.2 and images
were added with a Gaussian noise (μ=0, σ=0.1).
Generaly, interesting tissues in brain are gray matter
(GM), white matter (WM) and cerebrospinal fluid
(CSF). The MR phantom image was divided into
four clusters: GM, WM, CSF and background.
However, CSF and background have in general the
same gray level, so clusters number will be reduced
to three. In addition, synthetic image with two
classes is used as ‘ground truth’ for evaluation. The
first class corresponds to the gray level 0 whereas
the second class corresponds to the gray level 90.
Figure 1 (a) and (b) represent respectively the
original image and the image corrupted by additive
Gaussian noise. Figure 1 (c) shows the segmentation
result obtained by using FCM and figure 1 (d) shows
the result of RFCM. The RFCM successfully
segment MR image into three classes and
outperforms the FCM. Segmentation result of FCM
presents some spurious blobs of GM inside WM and
background.
The RFCM with higher value of α has
a smoothing effect and it reduces spurious blobs but
it can blur some fine details in the image which can
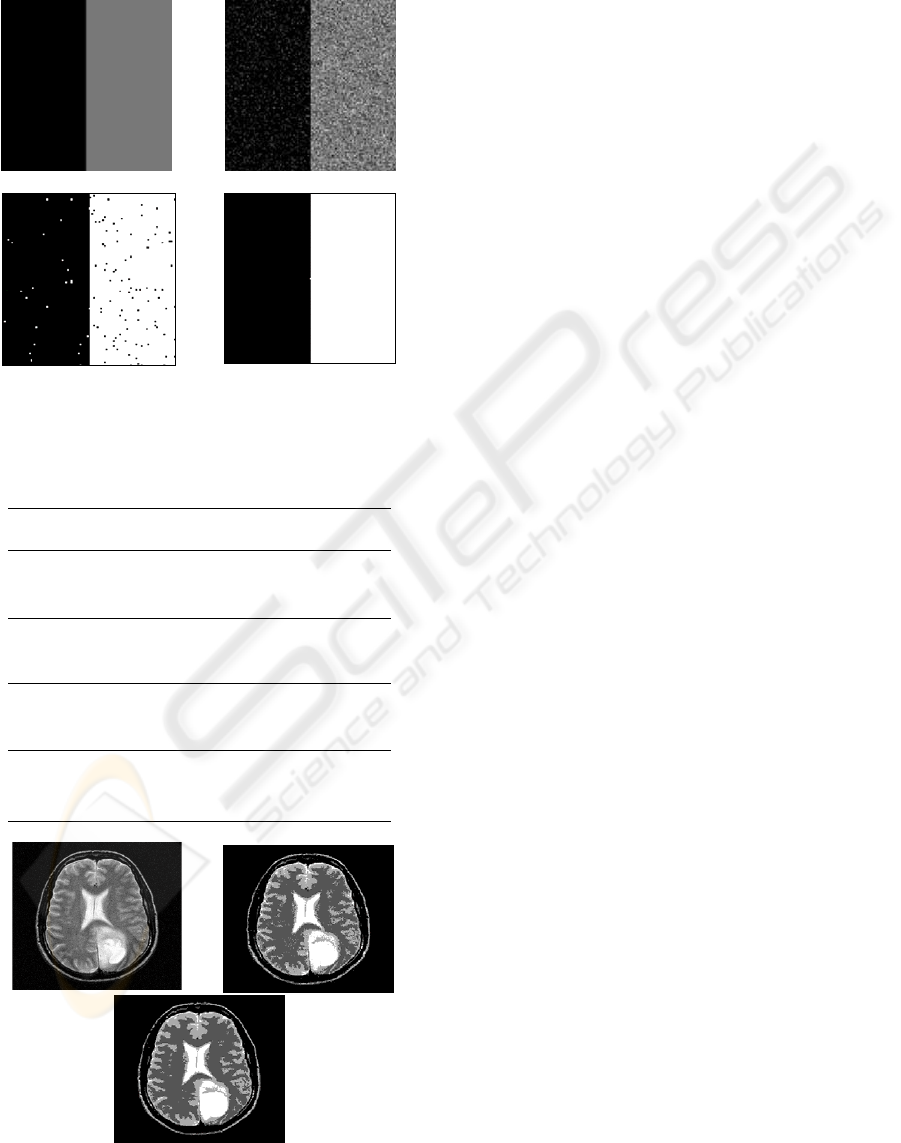
lose much of its sharpness. Figure 2 (a) and (b)
shows respectively the original synthetic image and
the degraded noisy image. The RFCM correctly
classify noisy pixels into clusters. The FCM did not
totally recover from noise, but successfully
segmented the image. The segmentation accuracy
(SA) measures are summarized in table 1. SA is
measured for different noise levels as follows:
(10)
From table 1, it can be observed that at 3% noise
level RFCM slightly outperform FCM. From where
we deduce that FCM is still competitive against
RFCM under light noise conditions.When the noise
level increases from 3% to 9%, the accuracy of FCM
decreases from 86% to around 72% and the accuracy
of RFCM decreases from 96% to around 95%.
Table 1: A summary of the accuracy (SA %) and the CPU
time of the two clustering methods on the phantom data
with different noise level: FCM and RFCM.
3% 5% 7% 9%
Accuracy %
F
CM
86.26 85.78 84.50 72.20
R
FCM
96.74 96.56 96.47 95.60
CPU time (sec)
F
CM
0.92 0.68 0.67 1.35
R
FCM
6.66 5.08 5.10 8.09
Besides the accuracy, computation cost among the
two methods is given in Table1. Because FCM is
based only on the gray level histogram of the data,
the CPU time of FCM is significantly lower than
those by RFCM in the same platform. Table 2
summarizes cluster validity value of the two
algorithms. In majority of cases, RFCM is superior
to FCM according to validity function. A further
experiment on real MRI image is given from a brain
image with tumor. The used image is a T2-weighted
MRI enhanced by contrast agent. Figure 3 (a) shows
the original image with additive noise. The
segmentation results are shown in Figure 3 (b) and
(c). Tumor in Figure 3 (a) is not considered as an
additional tissue class because it appears like CSF.
Since no ground truth for this image is available,
visual inspection shows that RFCM suppresses most
spurious blobs than FCM. Linear low-pass filtering
gives poor results as it yields even more edge
blurring and detail loss. However, method
incorporating spatial relationship directly in the
classification process can produce more meaningful
clusters.
4 CONCLUSIONS
In this work, we proposed an improved fuzzy-c-
means clustering algorithm which is robust to noise.
We modified the membership function in order to
incorporate spatial information. Pixel is classified
into its particular cluster by taking into account its
immediate neighbors membership function weighted
ROBUST FUZZY-C-MEANS FOR IMAGE SEGMENTATION
89
by a parameter α to control the neighborhood effect.
Thus, spurious blobs due to the presence of noise are
eliminated and the algorithm gives more
homogenous regions than other clustering methods.
Figure 2: (a) Original image; (b)image with Gaussian
noise, segmented image by (c) FCM; (d ) FCM(α=0.97).
Table 2: The clustering results of three images using
various FCM techniques.
Images Methods Vpc Vpe
Original MR
image
FCM 0.871 0.267
RFCM 0.967 0.040
Gaussian noise
added MR image
FCM 0.828 0.288
RFCM 0.939 0.081
Salt and pepper
added MR image
FCM 0.928 0.138
RFCM 0.979 0.037
Mixed noise
added MR image
FCM 0.804 0.334
RFCM 0.943 0.097
Figure 3: (a) MR image with additive noise. Segmented
image by (b) FCM; (c) RFCM(α = 0.25).
The proposed method seems to be more robust to
noise and it yields more homogenous labeling.
However, this method has a drawback of blurring
some fine details along the clustering process
especially for high value of the parameter α. Thus,
further works will emphasis on segmenting noisy
image by incorporation spatial information and
preserving image details.
REFERENCES
Ahmed, M.N., Yamany, S.M., Mohamed, N., Farag, A.A.
and Moriarty, T., 2002. A modified fuzzy c-means
algorithm for bias field estimation and segmentation of
MRI data. IEEE Trans. Med. Imaging, v21, 193-199.
Bezdek(a), J., Hall, L., Clarke, L., 1993. Review of MR
image segmentation using pattern recognition. Med
Phys, v20, 1033-1048.
Bezdek(b), JC., 1974. Cluster validity with fuzzy sets. J
Cybern, v3, 58-72.
Bezdek(c), JC., 1975. Mathematical models for systematic
and taxonomy. In: proceedings of eigth international
conference on numerical taxonomy, San Francisco, pp
143-166.
Chen(a), W.J., Giger, M.L., Bick, U., 2006. A fuzzy c-
means (FCM)-based approach for computerized
segmentation of breast lesions in dynamic contrast
enhanced MRI images, Acad. Radiol, Vol. 13, No. 1,
pp. 63–72.
Chen(b), S.C., Zhang, D.Q., 2004. Robust image
segmentation using FCM with spatial constraints
based on new kernel-induced distance measure, IEEE
Trans. Syst. Man Cybern. B, vol.34, no.4, pp.1907–
1916.
Goldszal, A. F., Davatzikos, C., Pham, D. L., Yan, M. X.,
Bryan, H. R. N. and Resnick, S. M, 1998. “An image
processing system for qualitative and quantitative
volumetric analysis of brain images,” J. Comput.
Assist. Tomog, 22(5):827-37.
Leemput, K. V., Maes, F., Vandermeulen, D. and In
Suetens, P., 1999. Automated model-based tissue
classification of MR images of the brain, IEEE Trans.
Med. Imag, vol. 18, n
o
10, pp. 897-908.
Lyer, NS., Kandel, A., Schneider, M., 2002. Feature-
based fuzzy classification for interpretation of
mammograms. Fuzzy Sets Syst, 114:, pp. 271–80.
Pham, D.L., Prince, J.L., 1999. An adaptive fuzzy c-means
algorithm for image segmentation in the presence of
intensity inhomogeneities, Pattern Recognition
Letters, v.20 n.1, pp. 57-68.
Shen, S., Sandham, W., Grant, M., and Ster, A., 2005.
MRI Fuzzy Segmentation of Brain Tissue Using
Neighborhood Attraction with Neural-Network
(
d
)
(a)
(c)
(
b
)
(a)
(c)
(
b
)
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
90

Optimization, IEEE Trans. Inform. Technol. Biomed.
v9 i3. 459-467.
Yang, MS, Hu, YJ, Lin, KCR, 2002. (FCM)- based
Segmentation techniques for tissue differentiation in
MRI of Ophthalmology using fuzzy clustering
algorithms. Magn Reson Imaging, 20: pp.173-179.
ROBUST FUZZY-C-MEANS FOR IMAGE SEGMENTATION
91
