MODELING AND RENDERING THE GROWTH OF

SPELEOTHEMS IN REAL-TIME

Daniel Menin Tortelli and Marcelo Walter

Federal University of Pernambuco, Recife, Brazil

Keywords:

Caves, Stalactite, Stalagmite, Real-time graphics, Modeling of natural scenes and phenomena.

Abstract:

Among the many natural phenomena already studied in computer graphics research, the interior of caves

remains largely unexplored. We present in this paper a plausible approach, based on Geological studies, for

modeling the genesis and growth of speleothems. Speleothems are mineral depositions formed in caves, such

as stalactites, stalagmites and columns. Our approach takes advantage of the new geometry shader, present

in the new generation of GPUs, and can generate in a controlled way, a large variety of cave scenes, with

meaningful geological parameters.

1 INTRODUCTION

In Computer Graphics as a research ﬁeld, researchers

have always been attracted to reproduce the beauty

of Nature and the intrinsic complexity in many sev-

eral phenomena, such as rain simulation (Rousseau

et al., 2006), illumination models and shading for

clouds (Bouthors et al., 2006), ﬁre simulation (Min

and Metaxas, 2007), among many more phenomena.

Since the initial efforts in this subject (Blinn et al.,

1983), it was obvious that the simulation of natural

phenomena is scientiﬁcally a great challenge, because

it potentially deals with a great volume of data and a

high computational demand, if all the mathematical

and physical complexity of the real models are taken

into consideration. Nature is able to create many com-

plex details. One example of this complexity is the

genesis and growth of speleothems such as stalac-

tites and stalagmites, found in the interior of lime-

stone caves. Among the many natural phenomena al-

ready studied in computer graphics research, the inte-

rior of caves remains largely unexplored. We present

in this paper a plausible approach, based on Geolog-

ical studies, for modeling the genesis and growth of

speleothems. Speleothems are mineral depositions

formed in caves, such as stalactites, stalagmites and

columns. Our approach takes advantage of the new

geometry shader, present in the new generation of

GPUs, for growth of speleothems in realtime using

meaningful geological parameters.

2 RELATED WORK

The great variety and beauty of speleothems struc-

tures has been a source of curiosity and a mystery

for hundreds or even thousands of years. Scientiﬁc

studies in such different areas as Physics, Chemistry,

Mathematics, and Geology, try to explain the origin

and growth of these speleothems. In (Short et al.,

2005b), Short and colleagues describe the process of

stalactite growth as a free-boundary problem, analyz-

ing the dynamics of the responsible ﬂuids for its for-

mation. In (Short et al., 2005a), the same group pre-

sented the ﬁrst free-boundary approach to the axisym-

metric growth of stalactites. They derived a law of

motion in which the local growth rate depends on the

radius and inclination of the stalactite’s surface. This

law holds under a set of limiting assumptions valid for

typical stalactite growth conditions. Numerical stud-

ies of this surface dynamics showed the existence of

an attractor in the space of shapes, toward which sta-

lactites will be drawn regardless of initial conditions.

Another work by the same group (Short et al., 2006),

describes the stalactite genesis and growth, with pa-

rameters similar to the ones described in (Short et al.,

2005b), speciﬁc for ice stalactites, known as icicles.

In this approach, the shape of the icicles also depends

on the initial parameters and of their future intera-

tions.

In (Szilder and Lozowski, 1995), a discreet three-

dimensional model was developed using a mathemat-

ical model of Random-Walk to simulate the growth

Menin Tortelli D. and Walter M. (2009).

MODELING AND RENDERING THE GROWTH OF SPELEOTHEMS IN REAL-TIME.

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 27-35

DOI: 10.5220/0001787200270035

 SciTePress

of icicles. That model is based on a series of parame-

ters supplied in the beginning of the simulation. The

values of those parameters vary with time along the

simulation, and they affect the shape of the stalac-

tite model directly. The water ﬂow along the icicle’s

surface is divided into ﬂuid elements which follow a

stochastic path towards the icicle tip. During its mo-

tion, a ﬂuid element may freeze on the icicle’s lateral

surface or at its tip. The ﬂuid elements may also drip

from the icicle tip.

In a rare example of computer graphics research in

this topic, a pioneering work by Yang and Ouhyoung

used fractal theory to model stalactites and stalag-

mites (Ouhyoung and Yang, 1993; Yang and Ouhy-

oung, 1992). To model the peculiar irregular shape of

speleothems, they used recursive and random subdivi-

sion on an initial simple geometric model. They also

used radiosity techniques (Sillion and Puech, 1994)

for illumination of the scene. They emphasize that

stalagmites are more difﬁcult to model because of

their much higher complexity. Therefore instead of

using fractal subdivision, they simulated these follow-

ing the natural process of erosion and accumulation.

In the results section we compare our results with one

of these papers ((Yang and Ouhyoung, 1992)) since

we did not have access to the other one. Finally, in

a paper about an intuitive painting interface for mak-

ing local deformations to 3D surfaces (Lawrence and

Funkhouser, 2004), the authors illustrate one possi-

ble result with a cave environment with stalactites and

stalagmites.

3 GEOLOGICAL BACKGROUND

According to (Lino, 2001), speleothems are mineral

depositions formed in caves, basically by chemical

processes of dissolution and precipitation. This char-

acteristic gives them a character of great permanence,

and which may even be structural. The most common

speleothems are stalactites, stalagmites and columns.

3.1 How the Speleothems Grow

In order to penetrate into the fractures of the lime-

stone rock, the rainwater, acidulated by atmospheric

and soil carbon-dioxide (CO2), dissolves it and car-

ries off the calcium carbonate until it ﬁnally emerges

on the roof of the cave. The drop of water suspended

on the roof of the cave is exposed to environmental

conditions, such as greater ventilation, alterations in

temperature, pH, and CO2 pressure. These environ-

mental conditions create chemical instability through

the liberation of the CO2 into the cave and the conse-

quent precipitation of part of the dissolved carbonate.

The drop of water hangs on the roof until it reaches

the volume and weight necessary to overcome surface

tension and fall. Hanging on the roof of the cave and

exposed to environmental conditions of the interior’s

cave, the surface of the drop develops the ﬁrst crys-

tals of calcite; these, organizing themselves during

the period in which the drop is still in contact with

the roof, form an initial crystalline ring which will

serve as a base for a future stalactite. Drop by drop, a

hollow tubular stalactite grows in a downward direc-

tion. The drop, when it at last falls, carries with it a

solution of carbonate which slowly forms a sucession

of layers on the ﬂoor immediately below, and which

becomes a stalagmite. The opposing growth of stalac-

tites and stalagmites might ﬁnally result in the union

of the two, to form a column. Figure 1(a) and (b) show

examples of stalactites and stalagmites, respectively,

whereas (c) illustrates a column, formed by the union

of a stalactite with a stalagmite.

Figure 1: Real Speleothems: (a) Stalactites - (b) Stalagmites

- (c) Columns.

3.2 Speleothems Growth Stages

Still according to (Lino, 2001), the process of forma-

tion of the speleothems is divided into three different

stages (Figure 2). Each one of these stages have deter-

minant variables that interfere somehow in the shape,

dimensions, coloration and texture of the speleothems

formed through the mechanism of calcite precipita-

tion.

Water Acidulation Stage. In the ﬁrst stage, we

have to consider the external environment located

above of the interior of the limestone cave. The plu-

viometric index, rain periodicity, soil vegetal cover-

age, average temperature, and the chemistry compo-

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

Figure 2: Speleothems growth stages.

sition of the soil, among other less important factors,

will inﬂuence the generated spheleotems. A bigger

volume and regularity of the rain, determines an in-

crease in the ﬂow rate of acidulated water that reachs

the cave roof. The drops remain a short time sus-

pended in the cave roof, just to be quickly replaced by

others. Thus, a little quantity of carbonate will be de-

posited in the cave roof. In other words, considering a

reasonable saturation level, the stalactites in this place

will be small or even not present, and the stalagmites

will have a fast growth and/or voluminous shape. On

the other hand, if the water volume decreases, the ten-

dency is that the stalactites are larger than the stalag-

mites. Also, if there aren’t enough amount and regu-

larity of rain, neither one of the speleothems will be

formed or they will have their growth interrupted until

satisfactory rain values are reached.

Limestone Dissolution Stage. In the second stage,

we consider the thickness of the rocky layer, degree

of purity, crack level, and solubility. This proper-

ties will conditionate the saturation level of the so-

lution, the access channels to the cave, and the kind

of minerals that will be dissolved and blended with

the saturated solution, thus deﬁning the characteristic

of the speleothem that will be formed. The degree of

purity of the rocky layer, for example, can inﬂuence

directly the coloring of the speleothems. In general,

speleothems have a white coloration due to their cal-

careous nature. However, the presence of others min-

erals such as iron, copper, manganese and malachite,

when blended with the solution, add a characteristic

pigmentation to the speleothem.

Mineral Deposition Stage. In the third stage, fac-

tors related to the interior of cave will deﬁne the typol-

ogy of the speleothems. The ﬁrst aspect to consider is

the morphology and dimensions of the underground

space - planar or inclined roof, abyss, great saloons,

ﬂoor under water, etc. For example, to achieve the

cave, if a drip of saturated solution does not ﬁnd a

propitious environment for which there is the dripping

(interior space), the process of growing is interrupted.

The second aspect to consider is the interrelation be-

tween the internal cave environment and the exter-

nal cave environment. This interrelation implicates in

larger or smaller water and air circulation. Thus, reg-

ularity and perpendicularity of the speleothems, such

as stalactites, can be modiﬁed due to circulation of air

coming from the external environment between the

corridors of the cave. Such circulation causes a de-

formation in the normal growth form of the stalactite,

changing its direction, not only vertically, but also

horizontally.

A better understanding of the concepts of forma-

tion of caves and speleothems in general, can be found

in (Lino, 2001; Kaufmann, 2003; Self and Hill,

2003).

4 OUR MODEL

This section details how our model was developed

and implemented. Since it is a simple model of the

growth of speleothems, we used approximations to

the real physical-chemical processes previously de-

scribed. The goal of this model was to make an

approximation of the geometric shape and appear-

ance of speleothems, using the capabilities of the new

pipeline architecture of the Direct3D 10 (Blythe,

2006; Boyd, 2007). Primarily, a exploration of the

new capabilities of two pipeline stages: Geometry-

Shader (GS) and Stream-Output (SO). The GS stage

processes entire primitives. Its input is a full primitive

(three vertices for a triangle, two vertices for a line, or

a single vertex for a point). In addition, each primitive

can also include the vertex data for any edge-adjacent

primitives. This could include at most an additional

three vertices for a triangle or an additional two ver-

tices for a line. The GS also supports limited geome-

try ampliﬁcation and de-ampliﬁcation. Given an input

primitive, the Geometry Shader can discard the prim-

itive, or emit one or more new primitives. The SO

stage is designed for streaming primitive data from

the pipeline to memory on its way to the rasterizer.

Data can be streamed out and/or passed into the ras-

terizer. Data streamed out to memory can be recircu-

lated back into the pipeline as input data or read-back

from the CPU.

MODELING AND RENDERING THE GROWTH OF SPELEOTHEMS IN REAL-TIME

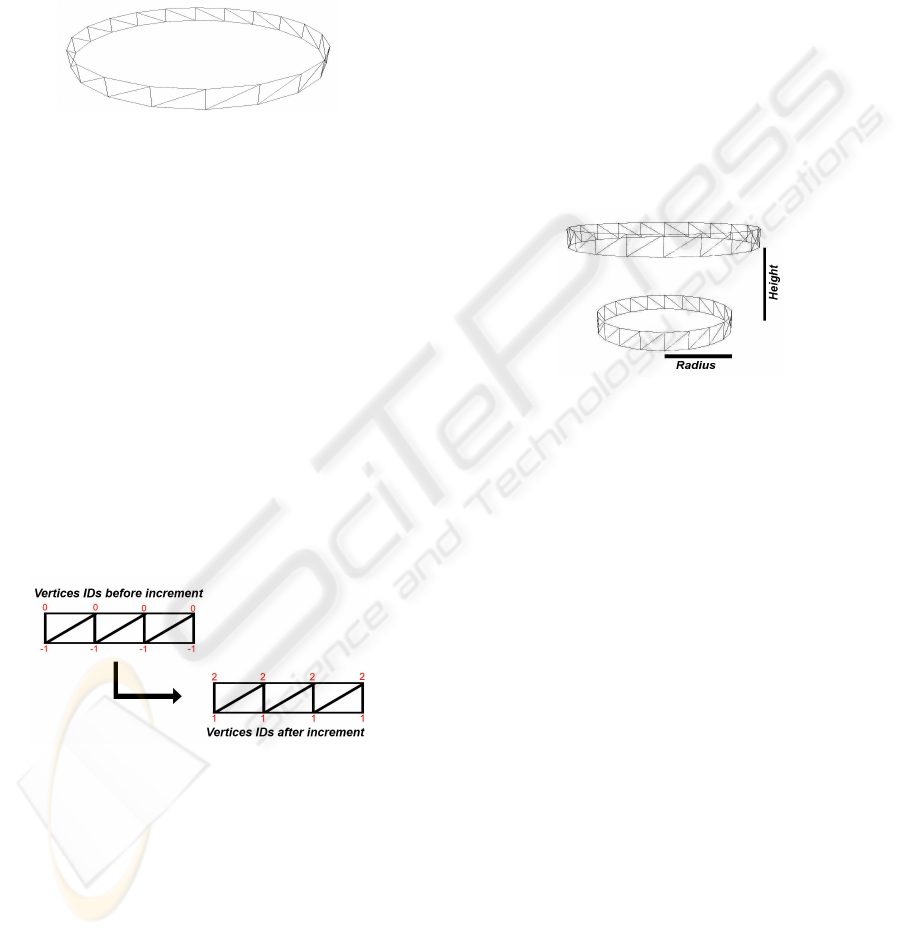
4.1 Shape of the Speleothem

When it starts, the application sends to the graphics

pipeline a primitive similar to a thin hollow cylinder

illustrated in Figure 3. Such primitive will be the ba-

sis for the creation of all speleothems in the simula-

tion. This primitive approximates the real initial cal-

cite crystalline ring.

Figure 3: Base Primitive (cylinder).

Besides the basic properties of each vertex, such

as position, normal vector, and texture coordinates,

we included an ID for each vertex of the base prim-

itive. These IDs will be a key element in the deﬁni-

tion of the shapes of the speleothems, and are used

to create the new primitives in the geometry-shader

stage, as we explain below. Once inside the pipeline,

the vertices pass through the vertex-shader stage and

reach the geometry-shader stage. Once there, the ver-

tices of the base will be used as information for cre-

ation of the new primitives. These primitives will

form the body of the speleothem. First, all the IDs of

the vertices of the primitive which are entering in this

stage will be increased by two. Figure 4 shows, re-

spectively, the vertices of the base primitive when en-

tering the geometry-shader stage and, later, with their

incremented IDs.

Figure 4: IDs increment.

After increasing the IDs, a new primitive is cre-

ated based on the base primitive. This new cylinder

is similar to the ﬁrst one. However, its shape is con-

trolled by two parameters generated by the applica-

tion, radius and height. The radius parameter mod-

els the diameter of the new primitive (cylinder). This

value is always minor or equal to the radius of the ear-

lier primitive (for stalactites), and any value for sta-

lagmites. This radius is randomly generated by the

application, following the variations previously de-

scribed.

The height parameter models the distance between

the base primitive and a new generated primitive. The

new primitive will be translated with respect to the

negative y− axis (stalactites) or to the positive y − axis

(stalagmites) according to the value of this parameter.

The height, similarly to the radius, is randomly gener-

ated by the application and passed to the shader effect

ﬁle as a constant buffer variable.

A summary of the possible effects on these vari-

ables (radius and height) and the type of structure gen-

erated is given in Table 1. The equation which deﬁnes

the new primitive, based on the radius and height sup-

plied by the application in relation to the earlier prim-

itive is given by v

= v +height + r ∗

N, where v

is the

new vertex position, v is the current vertex position,

N is the normal vector, and r represents the radius of

the new ring.

Figure 5: New generated primitive based in the parameters:

Radius and Height.

Figure 5 shows the base primitive and a new gen-

erated primitive inside the geometry-shader stage. For

the new cylinder, new IDs are assigned. The IDs for

the new primitive will be exactly the same IDs of the

base primitive when entering the pipeline for the ﬁrst

time, before the increment. In other words, highest

vertices of the cylinder receive IDs = 0 (zero) and the

lowest vertices receive IDs = -1. Finally, the last task

in the geometry-shader stage is to connect the vertices

of the ﬁrst and second cylinders. We use the IDs to

select only the vertices which will be processed for

the creation of the new primitive in the ring sequence.

Only vertices with IDs smaller than or equal to zero

are processed. Figure 6 shows the two previously gen-

erated cylinders and the link of their vertices, mak-

ing a cone-like shape. Also observe the conﬁguration

of the IDs after the ﬁrst pass through the geometry-

shader stage.

Using an approximation of the real model of

growth of speleothems described in (Kaufmann,

2003), the Radius and Height parameters, that con-

trol the speleothems growth rate and form, are de-

ﬁned as following. The pluviometric index level (PIL)

of the water acidulation stage, described in Section

3.2, is the amount of rain water. To our model, the

pluviometric index is one of three possible levels:

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

Figure 6: Cone-like shape created inside the geometry-

shader stage.

Level 0: lack of rain, in other words, no growth of

speleothems. Level 1: makes possible the creation

of stalactites, but there is no dripping, in other words,

the drop with saturated solution can solidify just in the

tip or in the surface of the stalactite already formed.

Level 2: Dripping of the saturated solution occurs due

to the high volume of rain water, possible growth of

stalagmites.

The drip interval depends on the pluviometric in-

dex, and the cracks in the limestone rock (ﬁssures

where the rain water ﬂows downward to the cave en-

vironment). The drip interval is inversely propor-

tional to the pluviometric index. If the drip interval

is small (wet weather), the tendency is an increase of

the new ring diameter. If the drip interval is long (dry

weather), the tendency is a decrease of the new ring

diameter. The radius parameter is linked with these

properties, and it is responsible to create some defor-

mities on the surface of the speleothem.

The calcium and carbon-dioxide concentration in

the drop of the satured solution depend on the soil

vegetal coverage, which is a source of carbon-dioxide

(CO2) for rain water. A soil with greater vegetation

cover increases the concentration of CO2 in water

(greater acidulation), making minerals such as cal-

cium and other minerals mixed with water that inﬁl-

trates in the layers of the limestone rock. The wa-

ter is super-saturated of calcium and, on entering the

cave, CO2 is degassed from the drop and the excess

calcium is deposited as calcite (CaCO3) in the cave.

The height parameter is linked with these properties.

Thus, the height of the speleothems is proportional to

the calcium and carbon-dioxide concentration.

Another possibility must be considered: if the cal-

cium and carbon-dioxide concentration are low, the

drops may solidify before reaching the tip of the sta-

lactite or the stalagmite base. Thus, only horizontal

growth takes place, rather than the vertical growth,

exactly at the point of the body of the speleothem

where the drip solidiﬁes. This horizontal displace-

ment is proportional to the value of radius of the

new primitive, where the drip with the saturated so-

lution solidiﬁed. This horizontal displacement cre-

ates some deformity on the surface of the speleothem.

The equation of the horizontal displacement is given

by: vd = k f ∗ arr/irr where vd is the vertex displace-

ment factor, k f is a ﬁxed scaling factor to adjust the

size of displacements proportionally to the size of the

speleothem, arr is the actual ring radius and irr is the

initial ring radius. Stalactites growth is linked with

two control variables: pluviometric index and CO2

concentration. Stalagmites growth is linked with both

pluviometric index and CO2 concentration, and also

with the drip interval. Table 1 shows all the properties

and the values that affect the height and radius of the

speleothems.

The presence of air circulation in the interior of

the cave also affects the shape of the speleothem. The

new primitive ring in formation can suffer a position

displacement in the direction of the air ﬂow. The pa-

rameter that models the presence or not of the air ﬂow,

as well as its direction, is supplied by the application

or by the interactive intervention of the user. It is com-

puted as

= wi(~v + ~w) where

is the new position

of vertex ~v, ~w is the unit vector deﬁning the wind di-

rection and wi is a scalar modeling the wind intensity

varying between 0.0 and 1.0. Figure 7 shows the de-

formation in the shape of stalactites given by random

wi values at each ring creation and also random ~w due

to the presence of air circulation in the interior of the

cave.

Figure 7: Effect of wind in the formation of stalactites.

The growth of speleothems is suspended due to

four factors: (i) the pluviometric index is in Level 0;

(ii) the radius of the new created ring is equal to zero;

(iiii) when the speleothem reaches the extremity of

the cave, i.e. roof (stalagmites) or ﬂoor (stalactites)

and (iv) when a column speleothem is created. When

any of these conditions is satisﬁed, the vertical growth

is suspended and only surface deformations and hori-

zontal growth of the speleothems will occur.

This step completes the process of geometry am-

pliﬁcation using the GS. However, in order for the

simulated speleothem to reach an approximate shape

of a real speleothem, it is necessary several successive

passes in the pipeline so that its full shape is reached.

At each pass, all the primitives created in the last pass

MODELING AND RENDERING THE GROWTH OF SPELEOTHEMS IN REAL-TIME

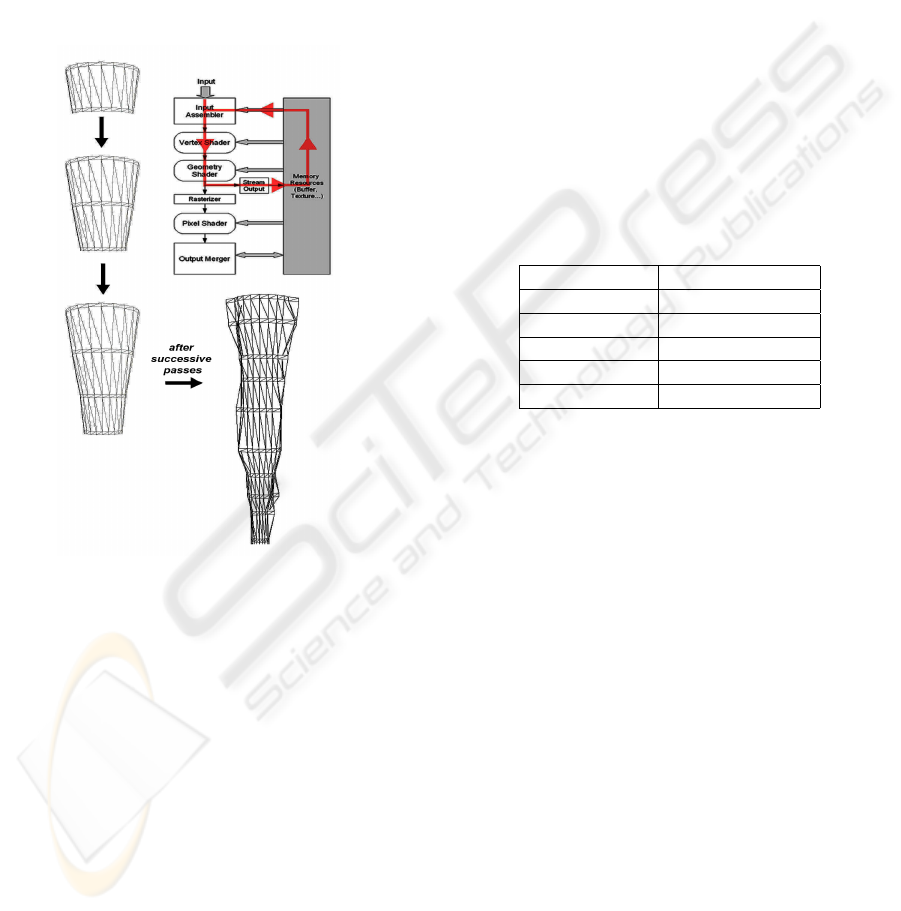
are the new input for the geometry-shader stage. For

that, the new primitive is sent back to the initial stages

of the pipeline, using the stream-output stage. Be-

fore passing the result to the next pipeline stages (ras-

terizer and pixel-shader), the data is stored in a spe-

cial buffer and sent to memory. The application takes

charge of rendering what was created, and also, of

sending back the same result to the initial stages of

the pipeline. Figure 8 shows the evolution in the con-

struction of the speleothems in the several successive

passes through the pipeline before the ﬁnal render.

Figure 8: Growth of the speleothem. Successive passes

through the pipeline.

4.2 Appearance of Speleothems

Once we have the shape deﬁned, we have to model

the appearance of the speleothems. According to

(Beynen et al., 2001), when visualized in visible or

transmitted light, the speleothems show variations of

hue and intensity. The standard coloration of the

speleothems is white due to the limestone. How-

ever, other minerals and impurities present in lime-

stone rock, can mix with the solution at the lime-

stone dissolution stage. Depending on the type of

mineral mixed, the speleothem will assume a charac-

teristic color of the same. For instance, the presence

of iron can produce ornamentations of red coloration,

ocher, brown, orange, and yellow. Manganese oxides

produce speleothems of black color, gray-bluish and

deep and brilliant blue. Copper salts produce blue

speleothems. The malachite produces blue-greenish

coloration. In our model the user can choose the min-

eral type that will produce a speciﬁc coloration for the

speleothem in formation. It is possible, on the ﬂy, to

change the rate of intensity of the mixture of the min-

eral in the solution, varying the color of speleothem.

Since we do not have a model for color distribution

along the body of the speleothem, we used a linear

variation from base to tip. To calculate this varia-

tion in coloring (ﬁnal vertex color), we use the equa-

tion: f vc = mc ∗ (arID/rc), where arID is the ac-

tual ring ID, rc is the amount of all the rings that the

speleothem is made off and mc is the mineral color

RGB data. The color will increase linearly according

to the current ring we are building. For our imple-

mentation, since the literature on this subject does not

present RGB data, we had to approximate the values

from pictures of the real speleothems. The RGB data

for each possible mineral is showed in Table 1.

Table 1: Mineral Color (mc).

Mineral Type RGB value

Calcareous (0.8, 0.8, 0.8)

Iron (0.87, 0.62, 0.34)

Manganese (0.32, 0.44, 0.54)

Copper (0.05, 0.7, 0.7)

Malachite (0.67, 0.82, 0.75)

Still in (Beynen et al., 2001), the crystals of

calcite which form the body of the speleothems are

translucent, thus providing great dispersion and re-

ﬂection when exposed to any type of lighting, and

ﬂuorescence in the visible spectrum when exposed

to UV light. Those optics properties are also at-

tributed to the mixed impurities to the solution in the

limestone dissolution stage. To improve the appear-

ance of the speleothems and to simulate the proper-

ties mentioned above, we used standard graphics tech-

niques such as Normal Mapping (Cohen et al., 1998;

Cignoni et al., 1998), Tone Mapping (Ashikhmin,

2002) and Environment Mapping (Blinn and Newell,

1976; Miller and Hoffman, 1976). Normal Mapping

is used to increase the effect of ruggedness on the sur-

face of the speleothems, together with the horizontal

displacement, described in Section 4.1. Tone Map-

ping and Environment Mapping are used for the effect

of brightness and reﬂection, simulating the properties

of crystals of calcita and moisture caused by aqueous

solution that covers the speleothems.

We need successive passes for the shape of the

speleothem to be completed. The actual number of

passes needed is entirely dependent on the random

values of the variables radius and height set by the ap-

plication. For that reason, for each new execution of

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

the application, we will have different speleothems. It

is also possible to create the speleothems in a manual

mode. The application interface allows to insert val-

ues for the parameters showed in the Table 2 through

interactive controls. These controls can also be used

to drive the creation of certain shapes of speleothems,

instead of creating them in a random way. During the

process of speleothems creation, is possible to do any

manipulation in the application such as changing val-

ues of parameters, camera navigation and also set pa-

rameters values for the Normal Mapping, Tone Map-

ping and Environment Mapping techniques.

Table 2: Parameters for speleothems growth.

PIL Drip Int. CO2 Conc. Type Radius Height

0 - - - - -

1 - low stalactite decrease x2 increase x1

1 - normal stalactite decrease x1 increase x2

1 - high stalactite same increase x3

2 dry low stalagmite decrease x1 increase x1

2 standard low stalagmite same increase x1

2 wet low stalagmite increase x1 increase x1

2 dry normal stalagmite decrease x1 increase x2

2 standard normal stalagmite same increase x2

2 wet normal stalagmite increase x1 increase x2

2 dry high stalagmite decrease x1 increase x3

2 standard high stalagmite same increase x3

2 wet high stalagmite increase x1 increase x3

5 RESULTS

In this section we illustrate a few of our results.

These were obtained on a Pentium D 2.8 GHz, 2GB

RAM, NVIDIA GeForce 8600 GT. The application

was implemented using the DirectX 10 API, HLSL

(St-Laurent, 2005). Figure 9 summarizes our results.

In (a) we show stalactites created by random values

of radius and height in according to the parameters

of Table 1. The values change at every application

time step. In (c) we show a stalactite growth with

LOW CO2 Concentration and all remaining param-

eters ﬁxed. In (b) we show a stalactite growth with

NORMAL CO2 Concentration and ﬁgure (d) shows

a stalactite growth with HIGH CO2 Concentration in

the drop of satured solutiuon. Figure 9 (e) shows

stalagmites with Drip Interval (DRY) and NORMAL

CO2 Concentration. The ﬁgure (f) shows columns

created by joining stalagmites and stalactites. Fig-

ures (g) and (h) show both stalactites and stalagmites

made with random values generated by the applica-

tion on-the-ﬂy. In the ﬁgures (a, b, c, f) the pre-

dominant mineral is calcareous, therefore the color

of speleothems is white. In ﬁgures (d, e, g) the pre-

dominant mineral is iron. The color of speleothems

vary between red and yellow. In ﬁgure (h) the pre-

dominant mineral is malachite which alters the color

to blue-greenish. The frame rate of our implemen-

tation depends on the amount of speleothems being

created. The amount is set in the beginning of the

simulation. Compared with the work of (Yang and

Ouhyoung, 1992), our model makes use of meaning-

ful geological parameters to control the shape and ap-

pearance of the speleothems. Our approach improves

the visual quality and also creates a simple shape with

a low polygon count, taking advantage of the Geome-

try Shader. Our approach is plausible with the growth

of real speleothems.

6 CONCLUSIONS

This work presented a simple model for growth of

speleothems in real-time, using real geological pa-

rameters of growth of speleothems. We also used

the powerful ampliﬁcation capability of the geometry-

shader and stream-output stages present in last gen-

eration GPUs. It is clear that the availability of

these two graphical pipeline stages becomes a rich

source for exploration of new forms to create geom-

etry. However, there is a lot to explore on this sub-

ject, not only in the simulation of this speciﬁc nat-

ural phenomena that is rich in information, but also

in the application side. We have not touched yet the

full richness of the way speleothems reﬂect light, and

this is left for future work. We assess that the ﬁ-

nal results were satisfactory compared with the real

forms of speleothems, making it possible to generate

a large variation of speleothems in realtime, suitable

for graphics applications.

ACKNOWLEDGEMENTS

We would like to thank professor Francisco da Cruz

(Chico Bill) from University of Sao Paulo, Brazil

(USP) who helped us with the geological background.

We also would like to thank professors Chuan-Kai

Yang and Ming Ouhyoung from National Taiwan

University of Science and Technology for making

available their results from the paper (Yang and Ouhy-

oung, 1992).

REFERENCES

Ashikhmin, M. (2002). A tone mapping algorithm for

high contrast images. In EGRW ’02: Proceedings of

the 13th Eurographics workshop on Rendering, pages

145–156, Aire-la-Ville, Switzerland, Switzerland. Eu-

rographics Association.

MODELING AND RENDERING THE GROWTH OF SPELEOTHEMS IN REAL-TIME

Beynen, P. V., Bourbonniere, R., Ford, D., and Schwarcz,

H. (2001). Causes of colour and ﬂuorescence in

speleothems. Chemical Geology, 175(3-4):319–341.

Blinn, J., Gomez, J., Max, N., and Reeves, W. (1983). The

simulation of natural phenomena (panel session). SIG-

GRAPH Comput. Graph., 17(3):137–139. Chairman-

Charles A. Csuri.

Blinn, J. F. and Newell, M. E. (1976). Texture and reﬂec-

tion in computer generated images. Commun. ACM,

19(10):542–547.

Blythe, D. (2006). The direct3d 10 system. Proceedings of

ACM SIGGRAPH 2006, 25(3):724–734.

Bouthors, A., Neyret, F., and Lefebvre, S. (2006). Real-

time realistic illumination and shading of stratiform

clouds. In Eurographics Workshop on Natural Phe-

nomena, pages 41–50.

Boyd, C. (2007). The direct3d 10 pipeline. ACM SIG-

GRAPH 2007 courses, pages 52–109.

Cignoni, P., Montani, C., Scopigno, R., and Rocchini, C.

(1998). A general method for preserving attribute val-

ues on simpliﬁed meshes. In VIS ’98: Proceedings of

the conference on Visualization ’98, pages 59–66, Los

Alamitos, CA, USA. IEEE Computer Society Press.

Cohen, J., Olano, M., and Manocha, D. (1998).

Appearance-preserving simpliﬁcation. In SIGGRAPH

’98: Proceedings of the 25th annual conference on

Computer graphics and interactive techniques, pages

115–122, New York, NY, USA. ACM.

Kaufmann, G. (2003). Stalagmite growth and palaeo-

climate: the numerical perspective. Earth and Plane-

tary Science Letters, 214(1-2):251–266.

Lawrence, J. and Funkhouser, T. (2004). A painting in-

terface for interactive surface deformations. Graph.

Models, 66(6):418–438.

Lino, C. F. (2001). Cavernas: O Fascinante Brasil Sub-

terr

aneo. Gaia, S

ao Paulo.

Miller, G. S. and Hoffman, C. R. (1976). Illumination and

reﬂection maps: Simulated objects in simulated and

real environments. SIGGRAPH ’84 Advanced Com-

puter Graphics Animation seminar notes.

Min, K. and Metaxas, D. (2007). A combustion-based tech-

nique for ﬁre animation and visualization. The Visual

Computer, 23(9-11):679–687.

Ouhyoung, M. and Yang, C. (1993). The synthesis of a cav-

ern with eroded stalactites and stalagmites. Proc. of

CAD/Graphics’93, New Advances in Computer Aided

Design and Computer Graphics.

Rousseau, P., Jolivet, V., and Ghazanfarpour, D. (2006). Re-

alistic real-time rain rendering. Computers & Graph-

ics, 30(4):507–518.

Self, C. A. and Hill, C. A. (2003). How speleothems grow:

An introduction to the ontogeny of cave minerals.

Journal of Cave and Karst Studies, 65(2):130–151.

Short, M. B., Baygents, J. C., Beck, J. W., Stone, D. A.,

III, R. S. T., and Goldstein, R. E. (2005a). Stalactite

growth as a free-boundary problem: A geometric law

and its platonic ideal. Phys. Rev. Lett., 94(018510).

Short, M. B., Baygents, J. C., and Goldstein, R. E. (2005b).

Stalactite growth as a free-boundary problem. Physics

of Fluids, 17(8).

Short, M. B., Baygents, J. C., and Goldstein, R. E. (2006).

A free-boundary theory for the shape of the ideal drip-

ping icicle. Physics of Fluids, 18(8).

Sillion, F. and Puech, C. (1994). Radiosity and Global Illu-

mination. Morgan Kaufmann, New York.

St-Laurent, S. (2005). The COMPLETE Effect and HLSL

Guide. Paradoxal Press.

Szilder, K. and Lozowski, E. (1995). Simulation of ici-

cle growth using a three-dimensional random walk

model. Atmospheric Research, 36(3-4):243–249.

Yang, C. and Ouhyoung, M. (1992). A stalactite cave by

stochastic modeling with radiosity illumination. Proc.

of 1992 International Computer Symposium.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

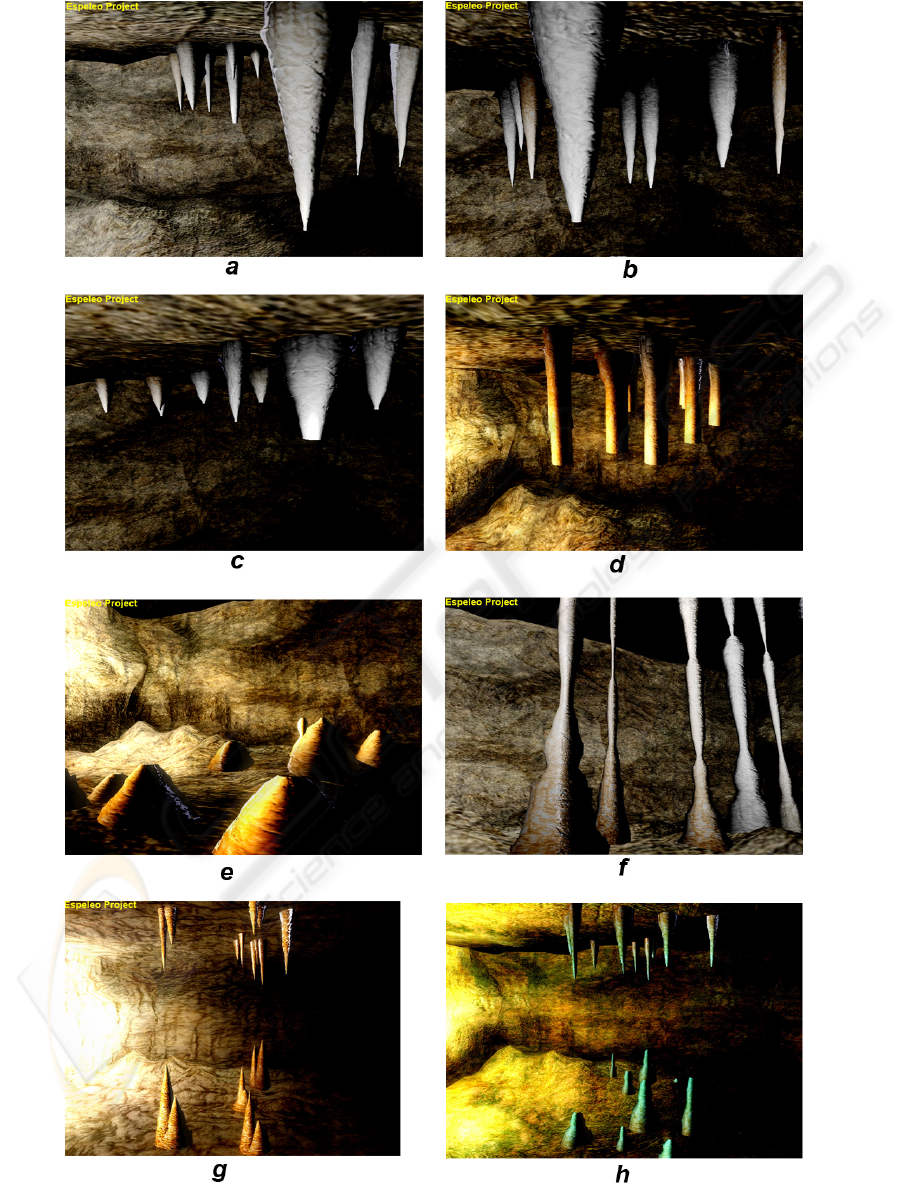
Figure 9: Virtual Speleothems.

MODELING AND RENDERING THE GROWTH OF SPELEOTHEMS IN REAL-TIME