
FAST APPROXIMATE NEAREST NEIGHBORS
WITH AUTOMATIC ALGORITHM CONFIGURATION
Marius Muja and David G. Lowe
Computer Science Department, University of British Columbia, Vancouver, B.C., Canada
Keywords:
Nearest-neighbors search, Randomized kd-trees, Hierarchical k-means tree, Clustering.
Abstract:
For many computer vision problems, the most time consuming component consists of nearest neighbor match-
ing in high-dimensional spaces. There are no known exact algorithms for solving these high-dimensional
problems that are faster than linear search. Approximate algorithms are known to provide large speedups with
only minor loss in accuracy, but many such algorithms have been published with only minimal guidance on
selecting an algorithm and its parameters for any given problem. In this paper, we describe a system that
answers the question, “What is the fastest approximate nearest-neighbor algorithm for my data?” Our system
will take any given dataset and desired degree of precision and use these to automatically determine the best
algorithm and parameter values. We also describe a new algorithm that applies priority search on hierarchical
k-means trees, which we have found to provide the best known performance on many datasets. After testing a
range of alternatives, we have found that multiple randomized k-d trees provide the best performance for other
datasets. We are releasing public domain code that implements these approaches. This library provides about
one order of magnitude improvement in query time over the best previously available software and provides
fully automated parameter selection.
1 INTRODUCTION
The most computationally expensive part of many
computer vision algorithms consists of searching for
the closest matches to high-dimensional vectors. Ex-
amples of such problems include finding the best
matches for local image features in large datasets
(Lowe, 2004; Philbin et al., 2007), clustering local
features into visual words using the k-means or sim-
ilar algorithms (Sivic and Zisserman, 2003), or per-
forming normalized cross-correlation to compare im-
age patches in large datasets (Torralba et al., 2008).
The nearest neighbor search problem is also of major
importance in many other applications, including ma-
chine learning, document retrieval, data compression,
bioinformatics, and data analysis.
We can define the nearest neighbor search prob-
lem as follows: given a set of points P = {p
1
,.. ., p
n
}
in a vector space X, these points must be preprocessed
in such a way that given a new query point q ∈ X,
finding the points in P that are nearest to q can be per-
formed efficiently. In this paper, we will assume that
X is an Euclidean vector space, which is appropriate
for most problems in computer vision. We will de-
scribe potential extensions of our approach to general
metric spaces, although this would come at some cost
in efficiency.
For high-dimensional spaces, there are often no
known algorithms for nearest neighbor search that
are more efficient than simple linear search. As lin-
ear search is too costly for many applications, this
has generated an interest in algorithms that perform
approximate nearest neighbor search, in which non-
optimal neighbors are sometimes returned. Such ap-
proximate algorithms can be orders of magnitude
faster than exact search, while still providing near-
optimal accuracy.
There have been hundreds of papers published on
algorithms for approximate nearest neighbor search,
but there has been little systematic comparison to
guide the choice among algorithms and set their inter-
nal parameters. One reason for this is that the relative
performance of the algorithms varies widely based on
properties of the datasets, such as dimensionality, cor-
relations, clustering characteristics, and size. In this
paper, we attempt to bring some order to these re-
sults by comparing the most promising methods on
a range of realistic datasets with a wide range of di-
mensionality. In addition, we have developed an ap-
proach for automatic algorithm selection and configu-
331
Muja M. and G. Lowe D. (2009).
FAST APPROXIMATE NEAREST NEIGHBORS WITH AUTOMATIC ALGORITHM CONFIGURATION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 331-340
DOI: 10.5220/0001787803310340
Copyright
c
SciTePress

ration, which allows the best algorithm and parameter
settings to be determined automatically for any given
dataset. This approach allows for easy extension if
other algorithms are identified in the future that pro-
vide superior performance for particular datasets. Our
code is being made available in the public domain to
make it easy for others to perform comparisons and
contribute to improvements.
We also introduce an algorithm which modifies
the previous method of using hierarchical k-means
trees. While previous methods for searching k-means
trees have used a branch-and-bound approach that
searches in depth-first order, our method uses a pri-
ority queue to expand the search in order according to
the distance of each k-means domain from the query.
In addition, we are able to reduce the tree construc-
tion time by about an order of magnitude by limiting
the number of iterations for which the k-means clus-
tering is performed. For many datasets, we find that
this algorithm has the highest known performance.
For other datasets, we have found that an algo-
rithm that uses multiple randomized kd-trees provides
the best results. This algorithm has only been pro-
posed recently (Silpa-Anan and Hartley, 2004; Silpa-
Anan and Hartley, 2008) and has not been widely
tested. Our results show that once optimal parame-
ter values have been determined this algorithm often
gives an order of magnitude improvement compared
to the best previous method that used a single kd-tree.
From the perspective of a person using our soft-
ware, no familiarity with the algorithms is neces-
sary and only some simple library routines are called.
The user provides a dataset, and our algorithm uses
a cross-validation approach to identify the best algo-
rithm and to search for the optimal parameter val-
ues to minimize the predicted search cost of future
queries. The user may also specify a desire to ac-
cept a less than optimal query time in exchange for
reduced memory usage, a reduction in data structure
build-time, or reduced time spent on parameter selec-
tion.
We demonstrate our approach by matching image
patches to a database of 100,000 other patches taken
under different illumination and imaging conditions.
In our experiments, we show it is possible to obtain
a speed-up by a factor of 1,000 times relative to lin-
ear search while still identifying 95% of the correct
nearest neighbors.
2 PREVIOUS RESEARCH
The most widely used algorithm for nearest-neighbor
search is the kd-tree (Freidman et al., 1977), which
works well for exact nearest neighbor search in low-
dimensional data, but quickly loses its effectiveness
as dimensionality increases. Arya et al. (Arya et al.,
1998) modify the original kd-tree algorithm to use
it for approximate matching. They impose a bound
on the accuracy of a solution using the notion of ε-
approximate nearest neighbor: a point p ∈ X is an ε-
approximate nearest neighbor of a query point q ∈ X,
if dist(p,q) ≤ (1 + ε)dist(p
∗
,q) where p
∗
is the true
nearest neighbor. The authors also propose the use of
a priority queue to speed up the search in a tree by
visiting tree nodes in order of their distance from the
query point. Beis and Lowe (Beis and Lowe, 1997)
describe a similar kd-tree based algorithm, but use a
stopping criterion based on examining a fixed number
E
max
of leaf nodes, which can give better performance
than the ε-approximate cutoff.
Silpa-Anan and Hartley (Silpa-Anan and Hartley,
2008) propose the use of multiple randomized kd-
trees as a means to speed up approximate nearest-
neighbor search. They perform only limited tests, but
we have found this to work well over a wide range of
problems.
Fukunaga and Narendra (Fukunaga and Narendra,
1975) propose that nearest-neighbor matching be per-
formed with a tree structure constructed by clustering
the data points with the k-means algorithm into k dis-
joint groups and then recursively doing the same for
each of the groups. The tree they propose requires a
vector space because they compute the mean of each
cluster. Brin (Brin, 1995) proposes a similar tree,
called GNAT, Geometric Near-neighbor Access Tree,
in which he uses some of the data points as the cluster
centers instead of computing the cluster mean points.
This change allows the tree to be defined in a general
metric space.
Liu et al. (Liu et al., 2004) propose a new kind
of metric tree that allows an overlap between the chil-
dren of each node, called the spill-tree. However, our
experiments so far have found that randomized kd-
trees provide higher performance while requiring less
memory.
Nister and Stewenius (Nister and Stewenius,
2006) present a fast method for nearest-neighbor fea-
ture search in very large databases. Their method is
based on accessing a single leaf node of a hierarchi-
cal k-means tree similar to that proposed by Fukunaga
and Narendra (Fukunaga and Narendra, 1975).
In (Leibe et al., 2006) the authors propose an effi-
cient method for clustering and matching features in
large datasets. They compare several clustering meth-
ods: k-means clustering, agglomerative clustering,
and a combined partitional-agglomerative algorithm.
Similarly, (Mikolajczyk and Matas, 2007) evaluates
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
332
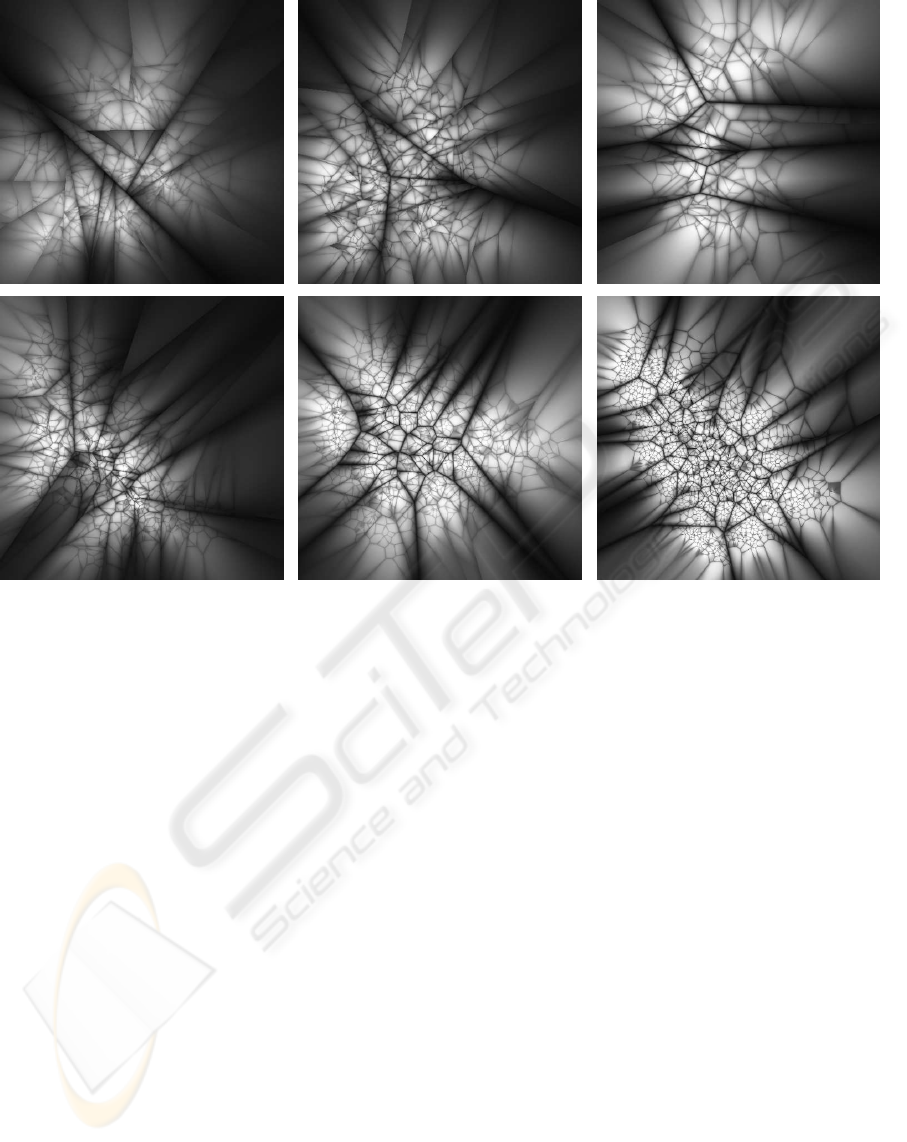
Figure 1: Projections of hierarchical k-means trees constructed using the same 100K SIFT features dataset with different
branching factors: 2, 4, 8, 16, 32, 128. The projections are constructed using the same technique as in (Schindler et al., 2007).
The gray values indicate the ratio between the distances to the nearest and the second-nearest cluster center at each tree level,
so that the darkest values (ratio≈1) fall near the boundaries between k-means regions.
the nearest neighbor matching performance for sev-
eral tree structures, including the kd-tree, the hierar-
chical k-means tree, and the agglomerative tree. We
have used these experiments to guide our choice of
algorithms.
3 FINDING FAST APPROXIMATE
NEAREST NEIGHBORS
We have compared many different algorithms for ap-
proximate nearest neighbor search on datasets with a
wide range of dimensionality. The accuracy of the ap-
proximation is measured in terms of precision, which
is defined as the percentage of query points for which
the correct nearest neighbor is found. In our exper-
iments, one of two algorithms obtained the best per-
formance, depending on the dataset and desired pre-
cision. These algorithms used either the hierarchical
k-means tree or multiple randomized kd-trees. In this
section, we will begin by describing these algorithms.
We give comparisons to some other approaches in the
experiments section.
3.1 The Randomized kd-tree Algorithm
The classical kd-tree algorithm (Freidman et al.,
1977) is efficient in low dimensions, but in high di-
mensions the performance rapidly degrades. To ob-
tain a speedup over linear search it becomes necessary
to settle for an approximate nearest-neighbor. This
improves the search speed at the cost of the algorithm
not always returning the exact nearest neighbors.
Silpa-Anan and Hartley (Silpa-Anan and Hartley,
2008) have recently proposed an improved version of
the kd-tree algorithm in which multiple randomized
kd-trees are created. The original kd-tree algorithm
splits the data in half at each level of the tree on the di-
mension for which the data exhibits the greatest vari-
ance. By comparison, the randomized trees are built
by choosing the split dimension randomly from the
first D dimensions on which data has the greatest vari-
ance. We use the fixed value D = 5 in our implemen-
tation, as this performs well across all our datasets and
does not benefit significantly from further tuning.
When searching the trees, a single priority queue
is maintained across all the randomized trees so that
FAST APPROXIMATE NEAREST NEIGHBORS WITH AUTOMATIC ALGORITHM CONFIGURATION
333

search can be ordered by increasing distance to each
bin boundary. The degree of approximation is deter-
mined by examining a fixed number of leaf nodes, at
which point the search is terminated and the best can-
didates returned. In our implementation the user spec-
ifies only the desired search precision, which is used
during training to select the number of leaf nodes that
will be examined in order to achieve this precision.
3.2 The Hierarchical k-means Tree
Algorithm
The hierarchical k-means tree is constructed by split-
ting the data points at each level into K distinct re-
gions using a k-means clustering, and then apply-
ing the same method recursively to the points in
each region. We stop the recursion when the num-
ber of points in a region is smaller than K. Figure
1 shows projections of several hierarchical k-means
trees constructed from 100K SIFT features using dif-
ferent branching factors.
We have developed an algorithm that explores the
hierarchical k-means tree in a best-bin-first manner,
by analogy to what has been found to improve the
exploration of the kd-tree. The algorithm initially
performs a single traversal through the tree and adds
to a priority queue all unexplored branches in each
node along the path. Next, it extracts from the prior-
ity queue the branch that has the closest center to the
query point and it restarts the tree traversal from that
branch. In each traversal the algorithm keeps adding
to the priority queue the unexplored branches along
the path. The degree of approximation is specified in
the same way as for the randomized kd-trees, by stop-
ping the search early after a predetermined number of
leaf nodes (dataset points) have been examined. This
parameter is set during training to achieve the user-
specified search precision.
We have experimented with a number of varia-
tions, such as using the distance to the closest Voronoi
border instead of the distance to the closest cluster
center, using multiple randomized k-means trees, or
using agglomerative clustering as proposed by Leibe
et al. (Leibe et al., 2006). However, these were found
not to give improved performance.
3.3 Automatic Selection of the Optimal
Algorithm
Our experiments have revealed that the optimal algo-
rithm for fast approximate nearest neighbor search is
highly dependent on several factors such as the struc-
ture of the dataset (whether there is any correlation
between the features in the dataset) and the desired
search precision. Additionally, each algorithm has a
set of parameters that have significant influence on
the search performance. These parameters include the
number of randomized trees to use in the case of kd-
trees or the branching factor and the number of itera-
tions in the case of the hierarchical k-means tree.
By considering the algorithm itself as a parame-
ter of a generic nearest neighbor search routine, the
problem is reduced to determining the parameters that
give the best solution. This is an optimization prob-
lem in the parameter space. The cost is computed as
a combination of the search time, tree build time, and
tree memory overhead. Depending on the application,
each of these three factors has a different importance:
in some cases we don’t care much about the tree build
time (if we will build the tree only once and use it for
a large number of queries), while in other cases both
the tree build time and search time must be small (if
the tree is built on-line and searched a small number
of times). There are also situations when we wish to
limit the memory overhead. We control the relative
importance of each of these factors by using a build-
time weight, w
b
, and a memory weight, w
m
, to com-
pute the overall cost:
cost =
s+ w
b
b
(s+ w
b
b)
opt
+ w
m
m (1)
where s represents the search time for the number of
vectors in the sample dataset, b represents the tree
build time, and m = m
t
/m
d
represents the ratio of
memory used for the tree (m
t
) to the memory used
to store the data (m
d
).
The build-time weight (w
b
) controls the impor-
tance of the tree build time relative to the search time.
Setting w
b
= 0 means that we want the fastest search
time and don’t care about the tree build time, while
w
b
= 1 means that the tree build time and the search
time have the same importance. Similarly, the mem-
ory weight (w
m
) controls the importance of the mem-
ory overhead compared to the time overhead. The
time overhead is computed relative to the optimum
time cost (s+ w
b
b)
opt
, which is defined as the optimal
search and build time if memory usage is not a fac-
tor. Therefore, setting w
m
= 0 will choose the algo-
rithm and parameters that result in the fastest search
and build time without any regard to memory over-
head, while setting w
m
= 1 will give equal weight to
a given percentage increase in memory use as to the
same percentage increase in search and build time.
We choose the best nearest neighbor algorithm
and the optimum parameters in a two step approach:
a global exploration of the parameter space followed
by a local tuning of the best parameters. Initially,
we sample the parameter space at multiple points and
choose those values that minimize the cost of equation
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
334
1. For this step we consider using {1,4,8, 16,32} as
the number of random kd-trees, {16,32,64,128,256}
as the branching factor for the k-means tree and
{1,5,10,15} as the number of k-means iterations. In
the second step we use the Nelder-Mead downhill
simplex method to further locally explore the param-
eter space and fine-tune the best parameters obtained
in the first step. Although this does not guarantee a
global minimum, our experiments have shown that
the parameter values obtained are close to optimum.
The optimization can be run on the full dataset or
just on a fraction of the dataset. Using the full dataset
gives the most accurate results but in the case of large
datasets it may take more time than desired. An op-
tion is provided to use just a fraction of the dataset
to select parameter values. We have found that using
just one tenth of the dataset typically selects parame-
ter values that still perform close to the optimum on
the full dataset. The parameter selection needs only
be performed once for each type of dataset, and our
library allows these values to be saved and applied to
all future datasets of the same type.
4 EXPERIMENTS
4.1 Randomized kd-trees
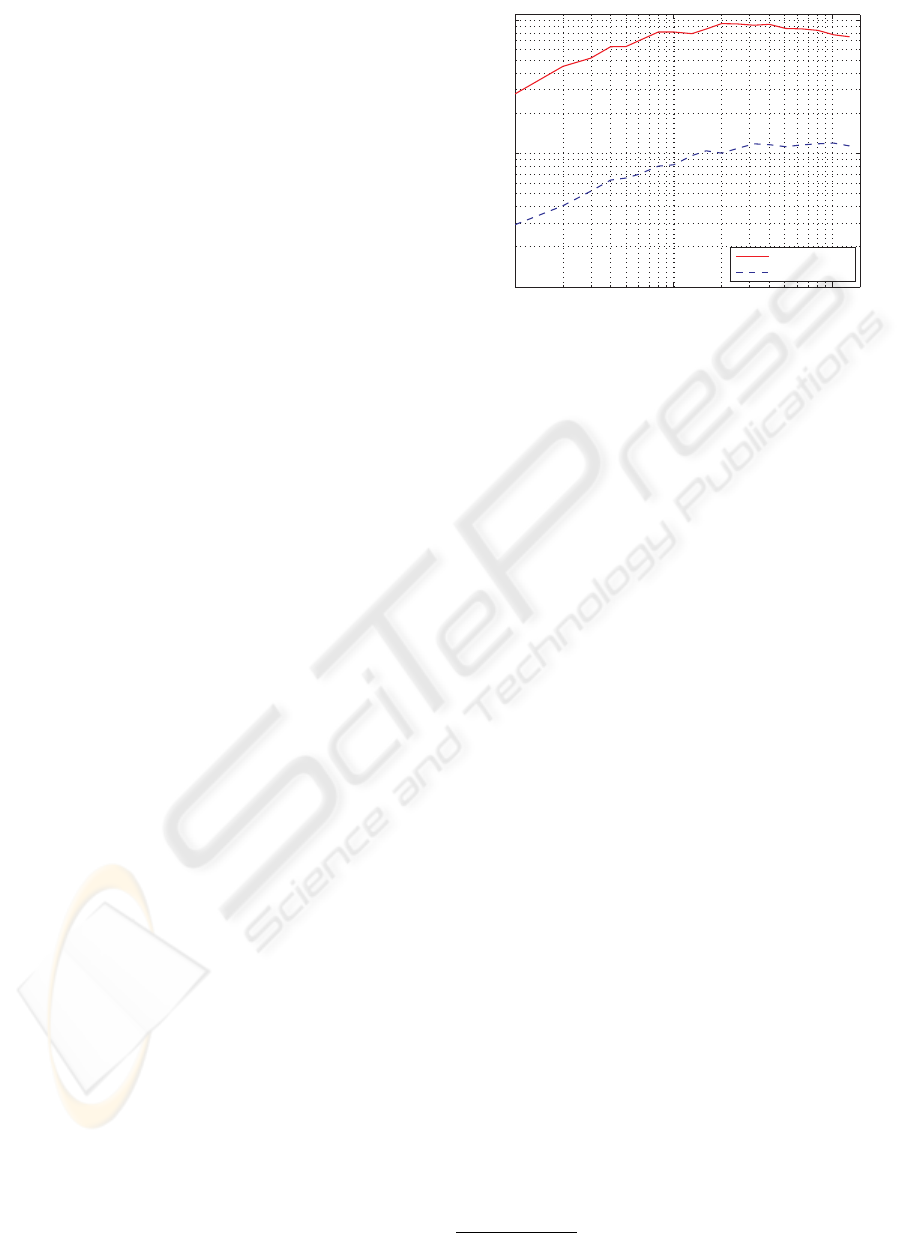
Figure 2 shows the value of searching in many ran-
domized kd-trees at the same time. It can be seen that
performance improves with the number of random-
ized trees up to a certain point (about 20 random trees
in this case) and that increasing the number of random
trees further leads to static or decreasing performance.
The memory overhead of using multiple random trees
increases linearly with the number of trees, so the cost
function may choose a lower number if memory us-
age is assigned importance.
4.2 Hierarchical k-means Tree
The hierarchical k-means tree algorithm has the high-
est performance for some datasets. However, one
disadvantage of this algorithm is that it often has a
higher tree-build time than the randomized kd-trees.
The build time can be reduced significantly by doing
a small number of iterations in the k-means clustering
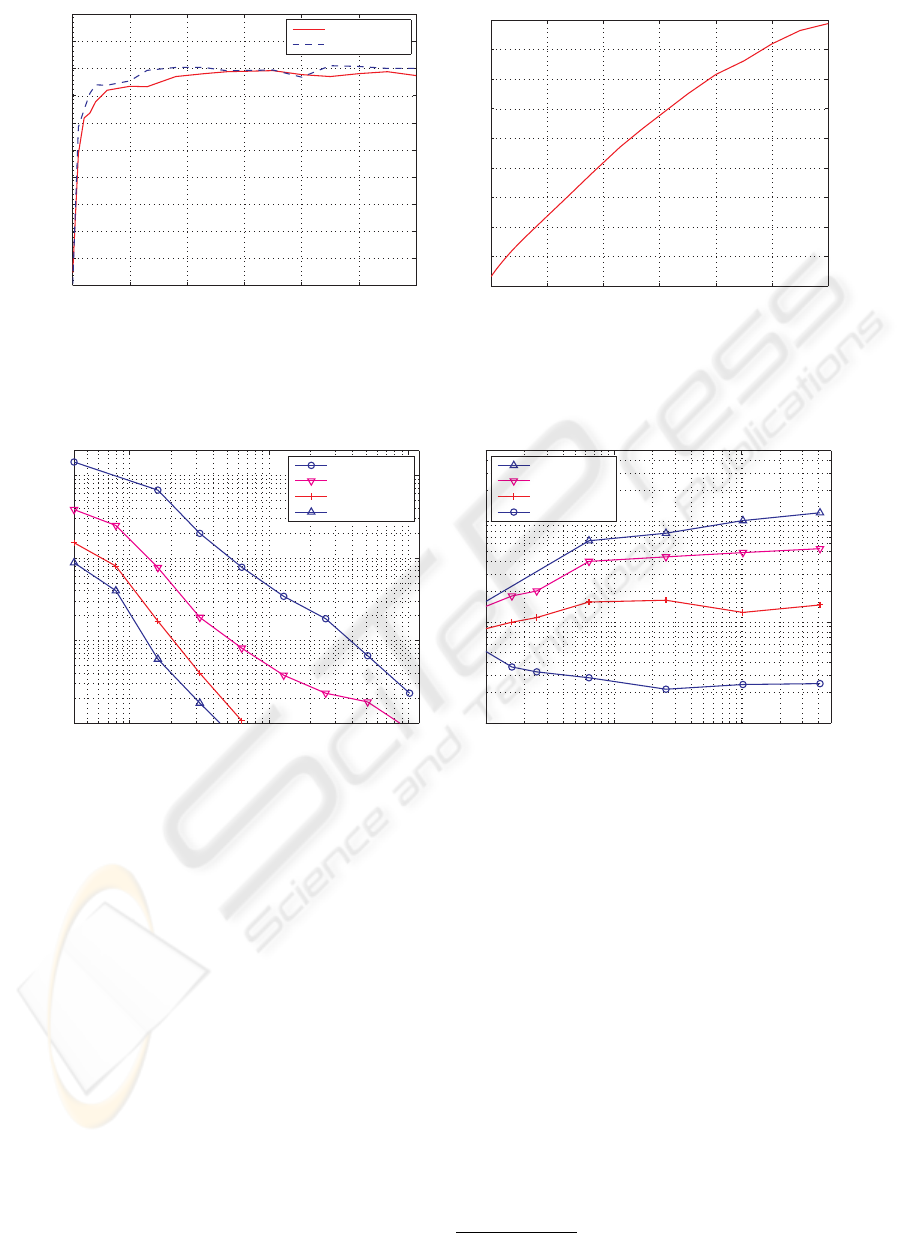
stage instead of running it until convergence. Figure 3
shows the performance of the tree constructed using a
limited number of iterations in the k-means clustering
step relative to the performance of the tree when the
k-means clustering is run until convergence. It can be
seen that using as few as 7 iterations we get more than
90% of the nearest-neighbor performance of the tree
10
0
10
1
10
2
10
0
10
1
10
2
Number of trees
Speedup over linear search
70% precision
95% precision
Figure 2: Speedup obtained by using multiple random kd-
trees (100K SIFT features dataset).
constructed using full convergence, but requiring less
than 10% of the build time.
When using zero iterations in the k-means cluster-
ing we obtain the more general GNAT tree of (Brin,
1995), which assumes that the data lives in a generic
metric space, not in a vector space. However figure
3(a) shows that the search performance of this tree is
worse than that of the hierarchical k-means tree (by
factor of 5).
4.3 Data Dimensionality
Data dimensionality is one of the factors that has a
great impact on the nearest neighbor matching per-
formance. Figure 4(a) shows how the search per-
formance degrades as the dimensionality increases.
The datasets each contain 10
5
vectors whose val-
ues are randomly sampled from the same uniform
distribution. These random datasets are one of the
most difficult problems for nearest neighbor search,
as no value givesany predictive information about any
other value. As can be seen in figure 4(a), the nearest-
neighbor searches have a low efficiency for higher di-
mensional data (for 68% precision the approximate
search speed is no better than linear search when the
number of dimensions is greater than 800). However
real world datasets are normally much easier due to
correlations between dimensions.
The performance is markedly different for many
real-world datasets. Figure 4(b) shows the speedup
as a function of dimensionality for the Winder/Brown
image patches
1
resampled to achieve varying dimen-
sionality. In this case however, the speedup does not
decrease with dimensionality, it’s actually increasing
for some precisions. This can be explained by the
1
http://phototour.cs.washington.edu/patches/default.htm
FAST APPROXIMATE NEAREST NEIGHBORS WITH AUTOMATIC ALGORITHM CONFIGURATION
335
0 10 20 30 40 50 60
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
Iterations
Relative search performace
70% precision
95% precision
(a)
0 10 20 30 40 50 60
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
Relative tree construction time
Iterations
(b)
Figure 3: The influence that the number of k-means iterations has on the search time efficiency of the k-means tree (a) and on
the tree construction time (b) (100K SIFT features dataset).
10
1
10
2
10
3
10
0
10
1
10
2
10
3
Dimensions
Speedup over linear search
20% precision
68% precision
92% precision
98% precision
(a) Random vectors
10
1
10
2
10
3
10
1
10
2
10
3
Dimensions
Speedup over linear search
81% precision
85% precision
91% precision
97% precision
(b) Image patches
Figure 4: Search efficiency for data of varying dimensionality. The random vectors (a) represent the hardest case in which
dimensions have no correlations, while most real-world problems behave more like the image patches (b).
fact that there exists a strong correlation between the
dimensions, so that even for 64x64 patches (4096 di-
mensions), the similarity between only a few dimen-
sions provides strong evidence for overall patch simi-
larity.
Figure 5 shows four examples of queries on the
Trevi dataset of patches for different patch sizes.
4.4 Search Precision
The desired search precision determines the degree of
speedup that can be obtained with any approximate
algorithm. Looking at figure 6(b) (the sift1M dataset)
we see that if we are willing to accept a precision as
low as 60%, meaning that 40% of the neighbors re-
turned are not the exact nearest neighbors, but just
approximations, we can achievea speedup of three or-
ders of magnitude over linear search (using the mul-
tiple randomized kd-trees). However, if we require
a precision greater then 90% the speedup is smaller,
less than 2 orders of magnitude (using the hierarchical
k-means tree).
We use several datasets of different dimensions
for the experiments in figure 6. We construct a 100K
and 1 million SIFT features dataset by randomly sam-
pling a dataset of over 5 million SIFT features ex-
tracted from a collection of CD cover images (Nister
and Stewenius, 2006)
2
. These two datasets obtained
by random sampling have a relatively high degree of
difficulty in terms of nearest neighbour matching, be-
cause the features they contain usually do not have
2
http://www.vis.uky.edu/
˜
stewe/ukbench/data/
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
336

Figure 5: Examples of querying the Trevi Fountain patch dataset using different patch sizes. The query patch is on the left
of each panel, while the following 5 patches are the nearest neighbors from a set of 100,000 patches. Incorrect matches are
shown with an X.
“true” matches between them. We also use the en-
tire 31 million feature dataset from the same source
for the experiment in figure 6(b). Additionally we use
the patches datasets described in subsection 4.3 and
another 100K SIFT features dataset obtained from a
set of images forming a panorama.
We compare the two algorithmswe found to be the
best at finding fast approximate nearest neighbors (the
multiple randomized kd-trees and the hierarchical k-
means tree) with existing approaches, the ANN (Arya
et al., 1998) and LSH algorithms (Andoni, 2006)
3
on
the first dataset of 100,000 SIFT features. Since the
LSH implementation (the E
2
LSH package) solves the
R-near neighbor problem (finds the neighbors within
a radius R of the query point, not the nearest neigh-
bors), to find the nearest neighbors we have used the
approach suggested in the E
2
LSH’s user manual: we
compute the R-near neighbors for increasing values
of R. The parameters for the LSH algorithm were
chosen using the parameter estimation tool included
in the E
2
LSH package. For each case we have com-
puted the precision achieved as the percentage of the
3
We have used the publicly available implementations
of ANN (http://www.cs.umd.edu/
˜
mount/ANN/) and LSH
(http://www.mit.edu/
˜
andoni/LSH/)
query points for which the nearest neighbors were
correctly found. Figure 6(a) shows that the hierar-
chical k-means algorithm outperforms both the ANN
and LSH algorithms by about an order of magnitude.
The results for ANN are consistent with the experi-
ment in figure 2, as ANN uses only a single kd-tree
and does not benefit from the speedup due to using
multiple randomized trees.
Figure 6(b) shows the performance of the random-
ized kd-trees and the hierarchical k-means on datasets
of different sizes. The figure shows that the two algo-
rithms scale well with the increase in the dataset size,
having the speedup over linear search increase with
the dataset size.
Figure 6(c) compares the performance of near-
est neighbor matching when the dataset contains true
matches for each feature in the test set to the case
when it contains false matches. In this experiment we
used the two 100K SIFT features datasets described
above. The first is randomly sampled from a 5 million
SIFT features dataset and it contains false matches
for each feature in the test set. The second contains
SIFT features extracted from a set of images forming
a panorama. These features were extracted from the
overlapping regions of the images, and we use only
FAST APPROXIMATE NEAREST NEIGHBORS WITH AUTOMATIC ALGORITHM CONFIGURATION
337

50 60 70 80 90 100
10
0
10
1
10
2
10
3
Correct neighbors (%)
Speedup over linear search
k−means tree − sift 100K
rand. kd−trees − sift 100K
ANN − sift 100K
LSH − sift 100K
(a)
50 60 70 80 90 100
10
0
10
2
10
4
10
6
Correct neighbors (%)
Speedup over linear search
k−means tree − sift 31M
rand. kd−trees − sift 31M
k−means tree − sift 1M
rand. kd−trees − sift 1M
k−means tree − sift 100K
rand. kd−trees − sift 100K
(b)
50 60 70 80 90 100
10
0
10
1
10
2
10
3
10
4
Correct neighbors (%)
Speedup over linear search
k−means tree − sift 100K true matches
rand. kd−trees − sift 100K true matches
k−means tree − sift 100K false matches
rand. kd−trees − sift 100K false matches
(c)
80 85 90 95 100
10
1
10
2
10
3
Correct neighbors (%)
Speedup over linear search
k−means tree
rand. kd−trees
(d)
Figure 6: Search efficiency. (a) Comparison of different algorithms. (b) Search speedup for different dataset sizes. (c) Search
speedup when the query points don’t have “true” matches in the dataset vs the case when they have. (d) Search speedup for
the Trevi Fountain patches dataset.
those that have a true match in the dataset. Our ex-
periments showed that the randomized kd-trees have
a significantly better performance for true matches,
when the query features are likely to be significantly
closer than other neighbors. Similar results were re-
ported in (Mikolajczyk and Matas, 2007).
Figure 6(d) shows the difference in performance
between the randomized kd-trees and the hierarchical
k-means tree for one of the Winder/Brown patches
dataset. In this case, the randomized kd-trees algo-
rithm clearly outperforms the hierarchical k-means al-
gorithm everywhere except for precisions very close
to 100%. It appears that the kd-tree works much better
in cases when the intrinsic dimensionality of the data
is much lower than the actual dimensionality, pre-
sumably because it can better exploit the correlations
among dimensions. However, Figure 6(b) shows that
the k-means tree can perform better for other datasets
(especially for high precisions). This shows the im-
portance of performing algorithm selection on each
dataset.
4.5 Automatic Algorithm and
Parameter Selection
In table 1, we show the results from running the pa-
rameter selection procedure described in 3.3 on the
dataset containing 100K random sampled SIFT fea-
tures. We have used two different search precisions
(60% and 90%) and several combinationsof the trade-
off factors w
b
and w
m
. For the build time weight,
w
b
, we used three different possible values: 0 rep-
resenting the case where we don’t care about the tree
build time, 1 for the case where the tree build time
and search time have the same importance and 0.01
representing the case where we care mainly about the
search time but we also want to avoid a large build
time. Similarly, the memory weight was chosen to be
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
338

Table 1: The algorithms chosen by our automatic algorithm and parameter selection procedure (sift100K dataset). The
“Algorithm” column shows the algorithm chosen and its optimum parameters (number of random trees in case of the kd-tree;
branching factor and number of iterations for the k-means tree), the “Dist. Error” column shows the mean distance error
compared to the exact nearest neighbors, the “Search Speedup” shows the search speedup compared to linear search, the
“Memory Used” shows the memory used by the tree(s) as a fraction of the memory used by the dataset and the “Build Time”
column shows the tree build time as a fraction of the linear search time for the test set.
Pr.(%) w
b
w
m
Algorithm Dist.
Error
Search
Speedup
Memory
Used
Build
Time
60%
0 0 k-means, 16, 15 0.096 181.10 0.51 0.58
0 1 k-means, 32, 10 0.058 180.9 0.37 0.56
0.01 0 k-means, 16, 5 0.077 163.25 0.50 0.26
0.01 1 kd-tree, 4 0.041 109.50 0.26 0.12
1 0 kd-tree,1 0.044 56.87 0.07 0.03
* ∞ kd-tree,1 0.044 56.87 0.07 0.03
90%
0 0 k-means, 128, 10 0.008 31.67 0.18 1.82
0 1 k-means, 128, 15 0.007 30.53 0.18 2.32
0.01 0 k-means, 32, 5 0.011 29.47 0.36 0.35
1 0 k-means, 16, 1 0.016 21.59 0.48 0.10
1 1 kd-tree,1 0.005 5.05 0.07 0.03
* ∞ kd-tree,1 0.005 5.05 0.07 0.03
0 for the case where the memory usage is not a con-
cern, ∞ representing the case where the memory use
is the dominant concern and 1 as a middle ground be-
tween the two cases.
Examining table 1 we can see that for the cases
when the build time or the memory overhead had the
highest weight, the algorithm chosen was the kd-tree
with a single tree because it is both the most memory
efficient and the fastest to build. When no importance
was given to the tree build time and the memory over-
head the algorithm chosen was k-means, as confirmed
by the plots in figure 6(b). The branching factors and
the number of iterations chosen for the k-means al-
gorithm depend on the search precision and the tree
build time weight: higher branching factors proved to
have better performance for higher precisions and the
tree build time increases when the branching factor or
the number of iterations increase.
5 CONCLUSIONS
In the approach described in this paper, automatic al-
gorithm configuration allows a user to achieve high
performance in approximate nearest neighbor match-
ing by calling a single library routine. The user need
only provide an example of the type of dataset that
will be used and the desired precision, and may op-
tionally specify the importance of minimizing mem-
ory or build time rather than just search time. All re-
maining steps of algorithm selection and parameter
optimization are performed automatically.
In our experiments, we have found that either of
two algorithms can have the best performance, de-
pending on the dataset and desired precision. One of
these is an algorithm we have developed that com-
bines two previous approaches: searching hierarchi-
cal k-means trees with a priority search order. The
second method is to use multiple randomized kd-
trees. We have demonstrated that these can speed the
matching of high-dimensional vectors by up to sev-
eral orders of magnitude compared to linear search.
The use of automated algorithm configuration will
make it easy to incorporate any new algorithms that
are found in the future to have superior performance
for particular datasets. We intend to keep adding new
datasets to our website and provide test results for
further algorithms. Our public domain library will
enable others to perform detailed comparisons with
new approaches and contribute to the extension of this
software.
ACKNOWLEDGEMENTS
This research has been supported by the Natural Sci-
ences and Engineering Research Council of Canada
and by the Canadian Institute for Advanced Research.
We wish to thank Matthew Brown, Richard Hartley,
Scott Helmer, Hoyt Koepke, Sancho McCann, Panu
Turcot and Andrew Zisserman for valuable discus-
sions and usefull feedback regarding this work.
FAST APPROXIMATE NEAREST NEIGHBORS WITH AUTOMATIC ALGORITHM CONFIGURATION
339

REFERENCES
Andoni, A. (2006). Near-optimal hashing algorithms for ap-
proximate nearest neighbor in high dimensions. Pro-
ceedings of the 47th Annual IEEE Symposium on
Foundations of Computer Science (FOCS’06), pages
459–468.
Arya, S., Mount, D. M., Netanyahu, N. S., Silverman, R.,
and Wu, A. Y. (1998). An optimal algorithm for ap-
proximate nearest neighbor searching in fixed dimen-
sions. Journal of the ACM, 45:891–923.
Beis, J. S. and Lowe, D. G. (1997). Shape indexing using
approximate nearest-neighbor search in high dimen-
sional spaces. In CVPR, pages 1000–1006.
Brin, S. (1995). Near neighbor search in large metric
spaces. In VLDB, pages 574–584.
Freidman, J. H., Bentley, J. L., and Finkel, R. A. (1977).
An algorithm for finding best matches in logarithmic
expected time. ACM Trans. Math. Softw., 3:209–226.
Fukunaga, K. and Narendra, P. M. (1975). A branch and
bound algorithm for computing k-nearest neighbors.
IEEE Trans. Comput., 24:750–753.
Leibe, B., Mikolajczyk, K., and Schiele, B. (2006). Effi-
cient clustering and matching for object class recogni-
tion. In BMVC.
Liu, T., Moore, A., Gray, A., and Yang, K. (2004). An inves-
tigation of practical approximate nearest neighbor al-
gorithms. In Neural Information Processing Systems.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. Int. Journal of Computer Vision,
60:91–110.
Mikolajczyk, K. and Matas, J. (2007). Improving descrip-
tors for fast tree matching by optimal linear projection.
In Computer Vision, 2007. ICCV 2007. IEEE 11th In-
ternational Conference on, pages 1–8.
Nister, D. and Stewenius, H. (2006). Scalable recognition
with a vocabulary tree. In CVPR, pages 2161–2168.
Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman, A.
(2007). Object retrieval with large vocabularies and
fast spatial matching. In CVPR.
Schindler, G., Brown, M., and Szeliski, R. (2007). City-
scale location recognition. In CVPR, pages 1–7.
Silpa-Anan, C. and Hartley, R. (2004). Localization us-
ing an imagemap. In Australasian Conference on
Robotics and Automation.
Silpa-Anan, C. and Hartley, R. (2008). Optimised KD-trees
for fast image descriptor matching. In CVPR.
Sivic, J. and Zisserman, A. (2003). Video Google: A text
retrieval approach to object matching in videos. In
ICCV.
Torralba, A., Fergus, R., and Freeman, W. T. (2008). 80
million tiny images: A large data set for nonpara-
metric object and scene recognition. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
30(11):1958–1970.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
340
