TEMPORAL VIDEO COMP

ESSION USING MODE FACTOR

AND POLYNOMIAL FITTING ON WAVELET COEFFICIENTS

T. Nithyaletchumy Devi, W. K. Lim, W. N. Tan, Y. F. Tan, H. T. Teng

Faculty of Engineering, Multimedia University, 63100 Cyberjaya, Selangor, Malaysia

Y. F. Chang

Faculty of Information and Communication Technology, Universiti Tunku Abdul Rahman

46200 Petaling Jaya, Selangor, Malaysia

Keywords: Temporal video compression, Wavelet transform, Haar wavelet, Polynomial fitting.

Abstract: The core idea of this study is to build an algorithm that functions to compress video sequences. The mode

value at every pixel along the temporal direction is calculated. If the frequency of the mode value satisfies a

predetermined frequency, then the intensity values for entire entries at that particular pixel position will be

changed to the mode value. The wavelet techniques will be applied to the pixels that do not satisfy the

predetermined frequency and followed by a polynomial fitting method. For the purpose of compression,

only the polynomial coefficients for pixels that do not satisfy the predetermined frequency, the mode values

for pixels that satisfy the predetermined frequency and the corresponding pixel positions will be stored. To

decompress, wavelet coefficients are estimated by the respective polynomials. The intensity values at the

intended pixel position are obtained by inverse wavelet transform for pixels that do not satisfy the

predetermined frequency. On the other hand, the stored mode values will be used to represent the intensity

values throughout the time interval. This method portrays a prospect to achieve an acceptable

decompressed video quality and compression ratio.

1 INTRODUCTION

On the whole, video compression denotes an act to

represent the details of a video sequence by means

of minimal data. Instead of transmitting all the

images, a code of the image representation will be

transmitted with a much smaller data size (Symes,

P.D., 2001). Furthermore, data can be compressed

before storage and transmission and decompressed

at the receiver, besides increasing the bandwidth

available (Symes, P.D., 2003). The two main

classification of compression are the lossless

compression and the lossy compression. These

methods have two main strategies, namely,

redundancy and irrelevancy respectively. In lossless

compression, the concentration is on obtaining

efficient ways of encoding the data. Additionally,

there will be no information that is irretrievably lost

in the process and it is exactly reversible. Whereas,

lossy compression transforms the image to have

simplified information and removes the data that we

can’t perceive in order to attain reduction in the file

size. It is an irreversible process that permanently

disposes some information. There are formats that

allow compression to as little as 1% but too much

compression may be dreadful as the changes

becomes visible and observable which can also

result to a video that can be hardly recognized

(Dunn, R.D., 2002).

Wavelet has extensively inspired both image and

video compression (Averbuch, A., 1996,

Koornwinder, T.H., 1993). With this basis, our

approach is to apply wavelet, to be precise, Haar, in

the temporal direction. The quintessence of this

study is to seek an algorithm to compress by

extracting only the perceptible element, thus

considerably reducing the data needed to be stored

whilst maintaining the adequate image quality.

Previously, the wavelet decomposition coefficients

which were generated using the Haar wavelet

(Figure 1) were applied on the pixel intensity values

160

Nithyaletchumy Devi T., Lim W., Tan W., Tan Y., Teng H. and Chang Y. (2009).

TEMPORAL VIDEO COMPRESSION USING MODE FACTOR AND POLYNOMIAL FITTING ON WAVELET COEFFICIENTS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 160-165

DOI: 10.5220/0001787901600165

 SciTePress

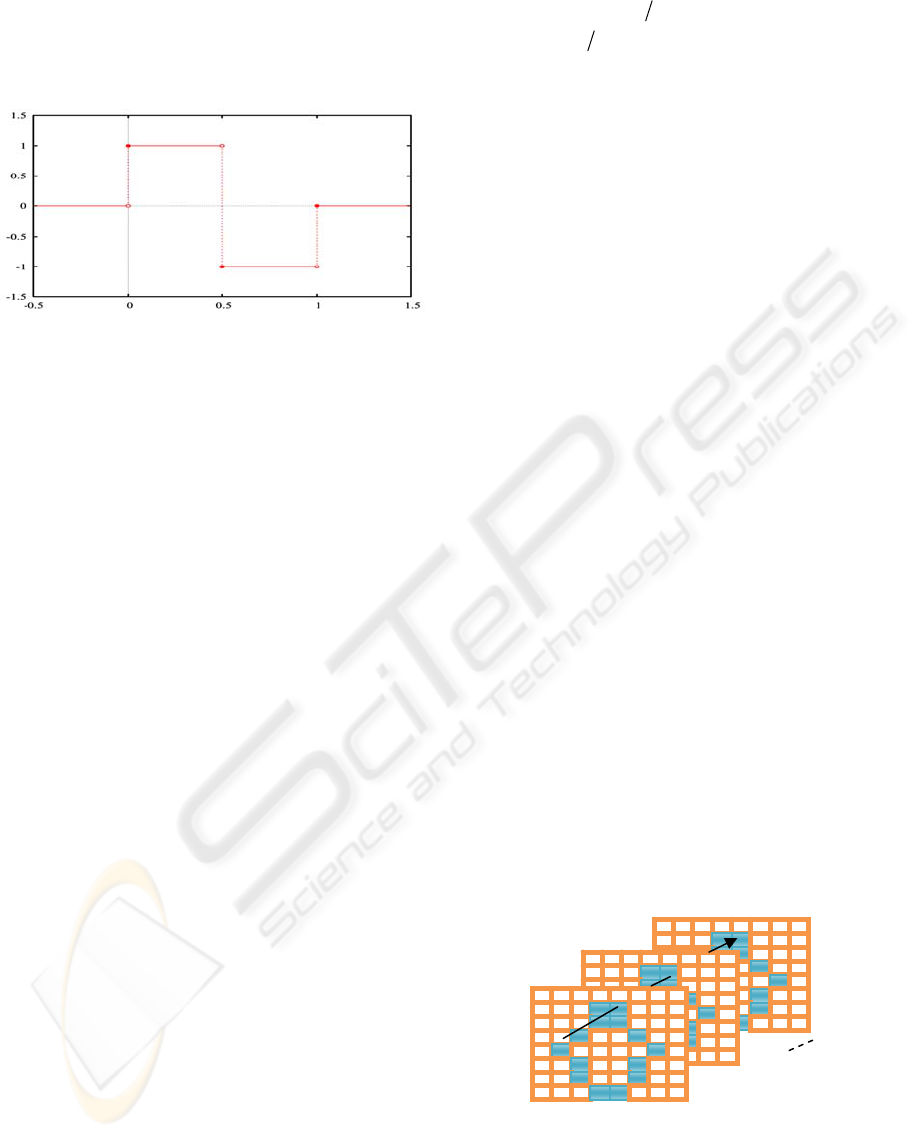
at all pixel positions and were approximated by a

polynomial of a fixed degree (T. Nithyaletchumy

Devi et al., 2008). It is a hybrid method with an

interest of wavelet related to a polynomial fitting.

Figure 1: The Haar Wavelet

()

In this study, the mode value at each pixel

position along the temporal direction is calculated.

Subsequently, the frequency of the mode value will

be compared to a predetermined percentage. Having

the acceptable value of frequency, substitutes all the

intensity values at the pixel position along the

temporal direction to have the mode value and stores

a single mode value for the entire temporal

direction. Pixel positions that did not satisfy the

predetermined frequency will have wavelet applied

on to obtain the wavelet decomposition coefficient

using the Haar wavelet and followed by polynomial

fitting of a fixed degree. Only the coefficients of the

polynomials at apiece pixel along the temporal

direction, the mode values for the pixels that satisfy

the predetermined frequency and the corresponding

pixel positions will be stored for the purpose of

compression. The decompression is done by

estimating the wavelet coefficients from the

polynomials with the stored coefficients and

retrieving the mode values at intended pixel position

throughout the time interval.

Even though, there are a wide variety of popular

wavelet algorithms such as the Daubechies wavelets,

Mexican Hat wavelets and Morlet wavelets which

have the advantage of better resolution for smoothly

changing motions but they are more expensive to

calculate than the Haar wavelets (Kaplan, I., 2004).

The Haar wavelet transform is theoretically trouble-

free and speedy, exactly reversible and handles well

over the edge effects that are a problem with other

wavelet transforms.

The Haar wavelet’s mother wavelet function

()

and its scaling function

()

are as described

below. Without loss of generality, we shall use the

same symbols for normalized wavelet and scaling

functions.

()

⎪

⎩

⎪

⎨

⎧

−=

otherwise

,121

,210

<≤

≤

and

()

⎩

⎨

⎧

otherwise

,10

≤ t

2 TEMPORAL COMPRESSION

AND DECOMPRESSION

In order to understand ways to modify an image, it is

only essential to master the way the computer stores

the image. Consider a

××

pixel gray scale

image, where

, the size of each frame and

the total number of frames considered. The

computer stores this image as a

matrix, with

each elements ranging from 0 to 255. At this

primary level,

is best sustained at powers of two

(e.g. 2, 4, 8, 16 etc.) as to permit a straight forward

distribution of data without any additional

manipulation as far as wavelet is concern.

In this study, first and foremost task is to

calculate the mode, denoted as , at each pixel

location

(

)

ji, along the temporal direction. Let

be the corresponding frequency of . For each

(

)

ji, , if

(

)

Tp ×%fr

≥

, 1000 ≤

p , then the pixel

location

(

)

ji,

will be stored in set , else it will be

in set

S . For each pixel location

(

in set ,

all intensity values along the temporal direction will

be changed to . For each pixel location

)

ji,

(

)

ji,

set , Haar wavelet decomposition method will be

applied. Illustrating this in a pictorial form (see

Figure 2 below), the pixel positions in set are not

shaded, whereas the pixel positions in set are

denoted by the shaded boxes.

Figure 2: The pixel positions in set are not shaded,

whereas the pixel positions in set are shaded.

Consider the pixels in , identify the intensity

values at the pixel position at every frame as

()

t=T

TEMPORAL VIDEO COMPRESSION USING MODE FACTOR AND POLYNOMIAL FITTING ON WAVELET

COEFFICIENTS

161

()

{

}

and for each

()

ji,

perform Haar wavelet

decomposition to the sequen

()

{

}

for n levels,

Nn ,...,2,1= :

()

∑∑∑

−

−nNk

kna

where

()

2,2 ∈−−+−

−

ktkqNdkt

ψφ

where

∑

−

−=

wv +

−n

()

−

∑

kqNd

kna

are the orthogonal subsp

ction space.

()

⎭

⎬

⎫

⎭

⎬

⎫

k 1−− N

, = Nq

aces of the

2 −

−

⎩

⎨

⎧

⎩

of our fun

⎨

⎧

−

decomposition

Two sets of coefficients, which are, the

approximation coefficients

()

{

}

and the detail

coefficients

()

{

}

,1 will be generated as shown in

Figure 3. Subsequently Haar wavelet

decomposition is reiterated to the approximation

coefficients sequence

()

, the

{

}

and obtain the

sequences

()

{

}

,2 and

()

{

}

,2 . This procedure

is persisted for say,

N nu times whereby N

signifies th f the decomposition and

it is depending on our preference. This will affect

the file size and quality which is the trade-off that

we will have to decide on.

avelet d

ber

vel

e w

ecomposition

e level o

Figure 3: Th

means of both t

sequen

tree.

detail coefficients

ces

() ( )

{

}

tNdtd

ijij

,,,,1 K and the

approximation coefficients sequence

()

{

}

tNa

, , the

original sequence

()

{

}

ly s

esse

can be re

ass

emble We

notice that the detail coefficients incl erous

values that are liter mall, predominantly due to

pixels comprising r movements along the

temporal direction. Then, we calculate the

cumulative values for the approximation coefficients

and the absolute values of the detail coefficients to

retain an increasing trend respectively. With that,

we are able to fit the cumulative values of the

respective coefficients using linear combinations of

polynomials of degree

de num

−

as follows:

−

∑

(1)

where are constant resolved for a prefe

value o

s to be rred

R,,2,1 K

For storage purpose,

is stored for each pixel

location i d the cn set an orresponding values of

for fitted polynomia on approximation and

detail coefficients are stored for each pixel location

in set

S . For decompression purposes, the intensity

values along temporal direction for each pixel

location in set

S are assigned the values of

q .

For each pixel location in set

S , the cumulative

values for both a proximation coefficients and detail

coefficients at any frame

[]

Tt ,1∈

can then be

estimated from the polynomial in

()

1 . Utilizing

these estimated cumulative values, we are able to

reconstruct the corresponding intensity values in a

lossy manner.

3 RESULTS A DISCUSSION

ell-

We tested the current study’s method using a w

known video sequence, “Akiyo”, with frame size

144176

pixels. Th o was independently

different d

is vide

scrutinized through first 16 and first 32 frames for

various

p at different levels of wavelets and fitted on

egrees of polynomial. Outcome of each

circumstance demonstrates the significance of the

role played by numbers of frames, frequency of

mode, level of the wavelet and degrees of

polynomial. The ensuing data are then compressed

using the discussed method, saved for

decompression and consequently the peak signal to

noise ratio (

PSNR) (Taubman, D.S. et al., 2002) of

each frame are computed using the following

formula.

⎟

⎞

⎜

⎛

255

PSN

()

t,1

()

t,2

()

tNd

()

t,2

⎠

⎜

⎝

Error SquareMean

log10

()

t,1d

()

tNa

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

162

Figure 4: PSNR versus p using the first 32 frames at level

2 and 3 of wavelet decomposition and different degree of

polynomial fitting.

sition level 2 and 3 at degree 2, 3

and 4. Prominently, for both 16 and 32 frames,

diff 2

sition process and the

pixels that

um, maximum and mean values of

mpo

Pre

: Result using the current study’s method

mode to be at least of the

to l

es used (16 and 32

polynomial degree (degree 2, 3 and

Size : Size of the information needed to be

PSNR : PSNR of each scenario

g the first 16 frames using p = 25, 50 and 75 at different levels

File Size (KB) Average PSNR CR

Figure 4 shows the PSNR versus p for p

ranging from 5 to 95, for 32 frames using Haar

wavelet decompo

erent degrees used for polynomial at level

wavelet decomposition does not bring significant

improvement in the

PSNR, whereas for 32 frames,

different degrees used for polynomial at level 3

shows a more significant improvement in the

PSNR.

Perhaps, this is due to the fact that a degree 3

polynomial fit exactly to the 4 data obtained on the

approximation coefficients.

The

p chosen is vital as it ascertains the

stringency on the minimum frequency that needed to

be obtained to segregate between pixels that go

through the wavelet decompo

will have all intensity values surrogated

with the mode value. From Figure 3, the optimum

p lies between 45 to 55 for the tested set of

parameters.

The degree chosen at each scenario is also

important because as the level of wavelet and degree

of polynomial increase, the number of data

concerned in generating the approximation

coefficients should possibly consist of at least the

minimum number of data needed to evaluate the

coefficients on that particular degree of polynomial.

This is an essential rule of thumb for analyzing

rationales. For an instance, applying a level 3

wavelet using the first 16 frames, it is not suitable to

use a degree 3 polynomial for its fitting as there will

only be two approximation coefficients, conversely,

we can do so using the first 32 frames.

Alternatively, in order to use a level of wavelet

decomposition that is higher than the number of data

obtained at the approximation coefficients, we may

chose to apply a lower degree of polynomial to the

approximation coefficients and a higher degree of

polynomial to the detail coefficients. This allows us

to evaluate the scenarios at a higher level but of

course with a natural increase in the file size bearing

in mind that higher polynomials produce more

coefficients.

The minim

Table 1: Minimum, maximum and mean values of PSNR usin

of wavelet and degrees of polynomial.

NR of each scenario are tabulated in Table 1

(using the first 16 frames) and Table 2 (using the

first 32 frames) in comparison with our previous

study’s method (T. Nithyaletchumy Devi et al.,

2008) and current study’s method, with

p = 25, 50

and

75 . In the previous method, the wavelet

deco sition coefficients were generated from the

pixel intensity values at all pixel positions. Then,

these coefficients were estimated by a polynomial of

a fixed degree at every pixel positions. The current

method on the other hand, applies polynomial fitting

only at pixel positions whereby the predetermined

frequency is not satisfied. By design, this reduces

the amount of information to be saved which has a

direct impinge on file size and compression ratio.

Information in the tables includes the following:

vious : Results using the previous study’s

method (wavelet applied to all pixel intensity

values)

Current

(conversed method)

p : Frequency of %p

ta number frames involved

Frames : Number of fram

frames)Level : The wavelet decomposition level

(level 2 and 3)

Degree : The

File

stored

Averag

CR : Compression ratio

Frames Level Degree Prev. Current Prev. Current Prev. Current

p=25 p=50 p=75 p=25 p=50 p=75 p=25 p=50 p=75

16 2 2 152,150 21,356 45,977 95,099 44.57 45.73 48.41 47.52 2.67 18.99 8.82 4.26

16 2 3 200,087 115,376 45.03 48.33 2.03 18.3 67 3.51 22,163 52,843 45.91 49.25 0 7.

TEMPORAL VIDEO COMPRESSION USING MODE FACTOR AND POLYNOMIAL FITTING ON WAVELET

COEFFICIENTS

163

Table 2: Minimum, maximum and mean o u e first 32 s p nd t levels

of wavelet and d ees o oly

File Size Average PSNR

values f PSNR sing th frame using = 25, 50 a 75 at differen

egr f p nomial.

Frames Level Degree

(KB) CR

Prev. Current Prev. Current Prev. Current

p=25 p=50 p=75 p=25 p=50 p=75 p=25 p=50 p=75

32 2 2 191,075 43,544 113,516 145,631 38.48 37.65 39.10 39.03 4.24 18.63 7.14 5.57

32 2 3 249,605 4 182,559 39.16 39.77 3.25 16.3 78 4.44 9,742 140,281 37.88 39.86 0 5.

32 2 4 3 58, 224,951 39.65 13.81 3.61 11,226 736 172,329 38.95 38.55 39.79 2.61 4.71

32 3 2 198, 1 1 39.073 44,222 15,799 42,197 23 39.98 39.66 39.66 4. 09 18.34 7.00 5.70

32 3 3 256,594 51,492 143,126 185,594 41.69 39.46 42.48 42.45 3.16 15.75 5.67 4.37

eral hav g c

inv d, en ging y

well-fitted line. Studying the results obtained, using

alte

proves,

16) of the

“Akiyo” video

es with level 2

degree 3 polynomial

act on

ent. In future,

Gen ly, in not mu h of movements

olve ga an polynomial would present a

o conversed method by means of 16 or 32 frames

seem to have an evidently improved result in the file

size

compared to using previous method. Also, even

though using more frames allows us to obtain a

tolerable file size and an acceptable compression

ratio, but the trade-off for the image quality would

be less efficient and not worth the compromise as

the diminution in the image quality is quite

prominent. Having compared the obtained

PSNR

values with other methods used in video

compression (Duanmu, C. J., 2006, Liang, J. et al.,

2005, Lin, K. K., et al., 2004, Zadeh, P. B., et al.,

2008), the results, as far as the

PSNR values are

concerned, they are comparable and are in a very

comfortable and acceptable range.

The mode factor portrays an obvious reduction in

file size as the frequency reduces. Although the

deviation in the

PSNR as the frequency changed is

not to a great extent, but the file size is notably

red. It also shows that, the reduction or

increment in the frequency will only result to a

certain level of improvement in the

PSNR.

Typically, the value of

PSNR is proportional to

the degree of polynomial and the level of wavelet

applied. At most events, as the degree of polynomial

increases at every level, the image quality im

as far as the mean value of

PSNR is concerned. In

addition, higher level of wavelet decomposition

allows enhanced analysis on the details of the

motions involved. For that reason, at every degree,

as the level is extended, the image quality is also

constantly improved. Even though higher degree of

polynomial and higher level of wavelet

decomposition engages more space, an

advantageous extent of improvement is preserved.

Additionally, increase in the number of frames yield

to decrease in the values of

PSNR. On the whole, the

proposed method emerges to evidently boast

positive upshot as the qualities of the images are

relatively elevated while delivering better

representations of the original images.

Figures 5(a) shows the original images from the

“Akiyo” video sequences at frames 1, 5, 8, 10, 12

and 16. Figures 5(b) and 5(c) below shows selected

frames (frames 1, 5, 8, 10, 12 and

4 CONCLUSION AN

SUGGESTIONS

decompressed images from the

sequences using the first 16 fram

wavelet decompositions and

fitting on both previous and proposed method

As for the findings and analyses, the range of

PSNR acquired using the first 16 frames results the

uppermost value of

PSNR seeing that lesser points

will have lesser deviation as far as accuracy is

concerned. Using 32 frames may grant a sensibly

reduced file size with a reasonable compression

ratio, but a massive concession on the image quality

has to be acknowledged. Nonetheless, engaging 16

frames distributes the most rationale results with a

balanced trade-off as far as efficiency and quality is

concerned. On average, using

50=p

appears to

have a higher

PSNR but the compromise in file size

is too massive.

Regardless of the method used, the highest value

PSNR is obtained when fewer frames are

considered. Even so, the desired option will be the

one with a good trade-off between the file size and

the

PSNR as they have a vast imp the storage

efficiency and the image quality respectively. The

proposed method of polynomial fitting applied to the

wavelet coefficients of the relevant pixels produced

a f ne outcome with anticipated level of efficiency as

far as compression is concerned.

Nonetheless, there exist certain limitations to this

conversed method where it is only more suitable for

video sequences with minimal motions and minor

changes in the background. Example of such

application is the storage of surveillance camera

footage or a closed-circuit television. This study is

still in the ground work and has heaps of rooms for

incessant advancement and enhancem

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

164

res

ames 1, 8, 12 and 16 using the

ent method at p=25.

SCAS’06, Vol. 2, 128-

Duanmu, C. J., 2006. Fast Scheme for the Four-step

Dunn, J.R., 2002. Faster Smarter Digital Video, Microsoft

Kap

Series Information,

Singapore:

Lia

ression. IEEE Trans. on Image

Lin . M., 2004. Wavelet Video Coding

its and Systems for Video Technology, Vol. 14,

Sym

Tau 2000:

Image Compression Fundamentals, Standards and

Practice, Kluwer Academic Publishers.

Zadeh, P.B., Buggy, T., Akbari, A.S., 2008. Statistical,

DCT and Vector Quantization-based Video Codec.

IET Image Processing, Vol. 2, Issue 3, 107-115.

olving a suitable level of wavelet and identifying

an appropriate degree of polynomial along with

suitable polynomials for different pixels throughout

the frames may be considered. Also, development of

a model to obtain the optimal

p for any domain of

dataset can be deemed. Color video sequence can

also be given a thought.

Figure 5(

first 16 frames o

a): Images of th

f the Akiyo v

e frames 1, 8, 12

ideo sequences.

and 16 using th

Figure 5(b): Images of frames 1, 8, 12 and 16 using the

first 16 frames using the previous method.

Figure 5(c): Images of fr

first 16 frames using the curr

FERENCES

Averbuch, A., Lazar, D. and Israeli, M., 1996. Image

Compression Using Wavelet Transform and

Multiresolution Decomposition. IEEE Trans. on

Image Processing, Vol. 5, Issue 1, 4 –15.

T.Nithyaletchumy Devi, Lim W.K., Tan Y.F., Tan W.N.,

Teng, H.T. and Chang, Y.F., 2008. Video

Compression Using Temporal Polynomial Fitting on

Wavelet Coefficients. 16

Int. Symposium of Science

and Mathematics (SKSM).

Duanmu, C. J., 2006. Fast Scheme for the Thee-step

Search Algorithm by the Utilization of Eight-bit

Partial Sums. 49

IEEE Int Midwest Symposium on

Circuits and Systems. In MW

131.

Search Algorithm in Video Coding. IEEE Int

Conference on Systems, Man and Cybernetics. In

SMC’06, Vol. 4, 3181-3185.

Press.

lan, I., 2004. Applying the Haar Wavelet Transform to

Time

http://www.bearcave.com/misl/misl_tech/wavelets/haa

r.html

ornwinder, T.H., 1993. Wavelets: An Elementary

Treatment of Theory and Applications,

World Scientific.

ng, J., Tu, C., Tran, T. D., 2005. Optimal Block

Boundary Pre/Postfiltering for Wavelet-based Image

and Video Comp

Processing, Vol. 14, Issue 12, 2151-2158.

, K. K., Gray, R

With Dependent Optimization. IEEE Trans. on

Circu

Issue 4, 542-553.

es, P.D., 2001. Video Compression Demystified,

McGraw Hill.

Symes, P.D., 2003. Digital Video Compression, McGraw

Hill.

bman, D.S., Marcellin, M.W., 2002. JPEG

TEMPORAL VIDEO COMPRESSION USING MODE FACTOR AND POLYNOMIAL FITTING ON WAVELET

COEFFICIENTS

165