
TRACKING MULTIPLE TARGETS BASED ON STEREO VISION
Ali Ganoun
LIVIC / LCPC, 14, route de la Minire - Btiment 824, 78000 Versailles, France
Thomas Veit, Didier Aubert
LIVIC / INRETS
Keywords:
Visual tracking, Multiple object tracking, Correspondence problem, Stereo vision.
Abstract:
This paper deals with the problem of tracking multiple objects in outdoor scenarios for the prospective of
intelligent vehicles. The input of the proposed algorithm is the result of a stereovision obstacle detection
algorithm. The aim is to establish the correspondence between the detected objects in consecutive frames and
to reconstruct the trajectory of each individual object. To this purpose, an object model based on its scene
position and its intensity caracteristic is defined. A track management strategy including track initiation, track
termination and track continuation is also proposed. This strategy enables to deal with issues such as object
appearance, dispapearance, occlusion and detection failure. An adaptive model update technique is applied in
order to take into account appearance variations of the tracked object along time. Experiments were carried out
in the context of pedestrian detection. Results on urban scenarios illustrate the performance of the proposed
method.
1 INTRODUCTION
Visual tracking is a key issue in the context of vi-
sion systems for intelligent vehicles. Several appli-
cation rely on an accurate trajectory estimation of the
monitored objects, for example pedestrian protection,
driver assistance, advanced safety and comfort en-
hancement. In this context, the tracking problem is
particularly challenging since targets have various dy-
namics and are subject to illumination as well as ap-
pearance changes. The aim of this paper is to address
the tracking problem for tracking multiple objects in
outdoor scenarios in the context of stereovision obsta-
cle detection. One of the critical issues is how solve
the correspondence problem, i.e. associate the detec-
tions corresponding to the same object in different im-
age frames.
The correspondence problem has been investi-
gated in different applications related to vision anal-
ysis such as video indexing, object recognition and
object tracking. One of the best known statistical
approaches used to solve the correspondence prob-
lem is the Joint Probabilistic Data-Association Filter
(JPDAF) (Fortmann et al., 1983). There are many
systems applying this method for tracking multiple
objects as in (Rasmussen and Hager, 2001). Unfor-
tunately, this technique assumes that the number of
tracks is known a priori and remains fixed in every
frame, so there is no possibility of obtaining incom-
plete trajectories. Another statistical technique is the
Multiple Hypothesis Tracker (MHT) (Reid, 1979). It
was designed for radar systems that need to track sev-
eral airplanes simultaneously. This method does not
have the same drawbacks as before and is able to han-
dle track initiation and termination. The main prob-
lem of the MHT is its high computational complexity
(Cox and Hingorani, 1996) arising from the fact that
several track hypotheses are maintained.
This paper describes a general framework for
tracking detected objects in the context of intelligent
vehicles. The goals is to determine a track for each de-
tected object. In (Muoz-Salinas et al., 2008) a similar
approach is proposed; our approach differs from their
solution in that it uses the grey level image instead of
color feature. Furthermore, they did not consider the
occlusions of the tracked targets. The work presented
in (Gavrila and Munder, 2007) uses a multi-cue ap-
proach combining stereovision, shape and texture in-
formation for pedestrian detection and tracking. The
detection and tracking are based on cascade modules
470
Ganoun A., Veit T. and Aubert D. (2009).
TRACKING MULTIPLE TARGETS BASED ON STEREO VISION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 470-477
DOI: 10.5220/0001789404700477
Copyright
c
SciTePress
each one with different visual criteria. The analysis
of tracks is similar to our approach. However, it uses
a weighted linear combination of Euclidean distance
between objects centroids and pairwise shape dissim-
ilarity.
Our multitarget tracker system consists of the fol-
lowing main steps: a Kalman filter for track predic-
tion, a gating based on the prediction step, a track
association and management strategy inspired by the
MHT algorithm, and a track update according to the
confidence in the association step. It has the following
features:
• It integrates 3D position and intensity characteris-
tics for the description model.
• It handles occlusions, incomplete trajectories,
track initiation and termination.
• It includes an adaptive method to update the de-
scription model (Nummiaro et al., 2003).
• It integrates the correlation cost function with the
distance between description models in a unified
framework (Medioni et al., 2001).
• It proposes a confidence measure used to evalu-
ate the tracking result without any need of ground
truth.
The performance of the tracking algorithm was
evaluated qualitatively and quantitatively on real im-
age sequences in the context of pedestrian detection.
The outline of this paper is the following: the
proposed algorithm is detailed in Section 2. Sec-
tion 3 introduces the evaluation framework. Section
4 presents experimental results and Section 5 gives
some concluding remarks.
2 TRACKING METHOD
Given a sequence of K frames, f
k
,[k ≤ K], for each
one there is a set of N
k
detected objects (or targets)
Ob
k
i
,i ∈ [0,N
k
],N
k
∈ [0, N], moving around in a 3D
world, where N is the number of objects in the se-
quence. Each object is associated with descriptor con-
sisting of a feature vector. This descriptor should be
as invariant as possible to appearance changes of the
object. A track is denoted as T
k
j
, j ∈ [0,M
k
],M
k
∈
[0,M], where M
k
is the number of tracks in the frame
f
k−1
, and M is the number of tracks in the sequence.
A feature vector is associated to the head of each track
T
k
j
as well as to each detected objects. Each track is
assigned a specific state.
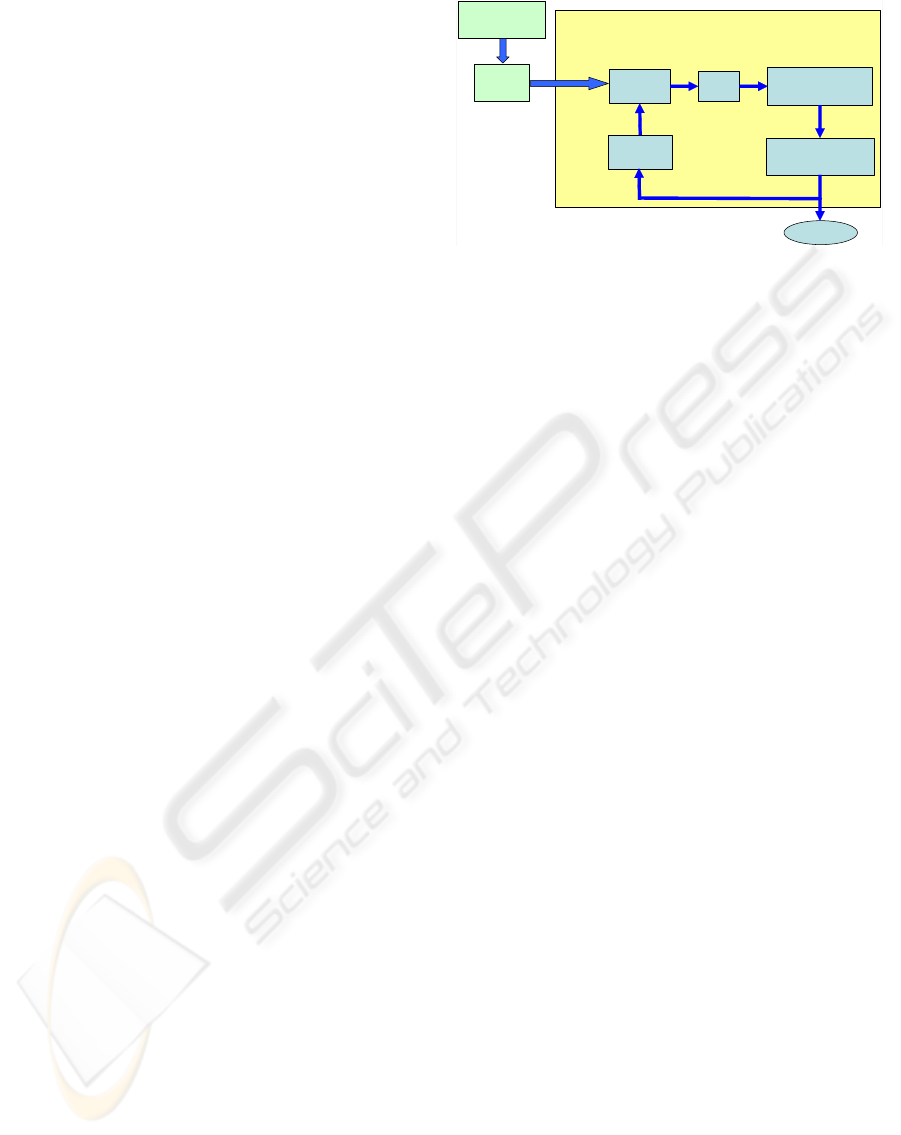
The main modules of the proposed tracker, shown
in Figure 1, are the following: Track Prediction, Track
Gating
Track update
Track
prediction
Track Management
New Detected
Objects
Track
Association
Confirmed Tracks
{Ob}
{T}
Detection
Stereo System
Tracking System
Figure 1: Overview of the proposed tracker modules, the
inputs are the list of detected objects, while the outputs are
the confirmed tracks
Association, Gating, Track Update and Track Man-
agement. The following subsections gives more de-
tails about each component, in addition to the target
description model used in the correspondence prob-
lem.
The input of the tracker is a list of detected objects,
with a description model for each object, while the
output is list of trajectories. Each trajectory consists
of a unique identification label, the current descriptor
and the velocity. The proposed tracker can be used
with any detector providing the 3D position of the ob-
ject in the scene and a region of interest in an image
from which to compute the intensity characteristics of
the object. As an example, the stereovision detection
algorithm proposed in (Labayrade et al., 2002) pro-
vides the required information.
2.1 Target Description Model
The aim of the target modeling is to select a set of
relevant features for representing the targets so that
each one can be distinguished from the other targets.
In this paper the target description model is based on
two characteristics: the 3D position, and an appear-
ance model represented in the form of a normalized
histogram using the grey level intensity distribution.
This combination is motivated by the fact that the his-
togram model alone cannot, in many cases, discrimi-
nate the target from the other objects, as many targets
may have the same grey level distribution. On the
other hand, the depth information cannot distinguish
between targets close to each other on the ground
plane (X,Z) , where the X axis is orthogonal to the
vehicle front axis and the image plane and the Z axis
corresponds to the depth.
TRACKING MULTIPLE TARGETS BASED ON STEREO VISION
471

2.2 Track Prediction
This process deals with the motion prediction of the
tracked objects. As the Kalman filter provides an es-
timation of system states and a prediction, it has been
used to predict the position of the target in the new
frame, with a constant velocity model for the target.
The 3D position of each target is predicted using
a simple linear Kalman filter with a state vector x =
[X,Z,
˙
X,
˙
Z]
T
, and a measurement vector y = [X,Z]
T
.
The X and Z correspond to the 3D target position on
the ground plane and
˙
X,
˙
Z represent the corresponding
velocities.
2.3 Track Association
To solve the assignment problem, we consider firstly
an assignment matrix A
k
= [a
i, j
] where the entries a
i, j
have the following meaning: a
i, j
= 1, if and only if
Ob
k
i
can be assigned to track T
k−1
j
and, otherwise,
zero. Thus the assignment matrix indicates possi-
ble correspondence between tracks and detected ob-
jects through the 3D space depending on the mod-
eling of their description models. Due to the com-
plexity of the tracked objects, false correspondences
are inevitable, so our objective is to limit the false
correspondences to the minimum. In real situations,
many assignment conflicts may arise either because
multiple tracks compete for one detected object or be-
cause multiple detected objects fit correctly to a single
track. We adopt a uniqueness constraint stating that
one track uniquely matches one detected object.
Secondly, we define the cost matrix as C
k
= [c
i, j
]
where c
i, j
reflects the difference between the fea-
ture vector (position and intensity histogram) of a
track T
k−1
j
and the feature vector of a detected ob-
ject Ob
k
i
. It is computed using the target descrip-
tion model through the following measures (Medioni
et al., 2001):
c
i, j
=
Corr
i, j
1 + d
i, j
(1)
Where Corr
i, j
∈ [−1, 1], represents the correlation be-
tween the grey level histogram ( i.e. the appearance
model) of Ob
k
i
and that of T
k−1
j
. d
i, j
∈ [0,∞], is the
Euclidean distance in the 3D real world between the
position of Ob
k
i
and the predicted position of T
k−1
j
.
From this relation we note that c
i, j
≈ 0 for similar tar-
get models, while penalizing distant models.
The number of tracked objects can vary between
frames, i.e., while searching for smooth set of tracks
there is the possibility of obtaining different num-
ber of tracks in each frame. When the number of
tracks increases, then that means the appearance of
a new object. In the other hand a decreasing of tracks
means either occlusion, or the tracked object leaves
the scene.
Usually two objects are considered similar if and
only if their similarity degree is smaller than a prede-
fined threshold λ. In other words c
i, j
set to ∞ and a
i, j
set to 0 if c
i, j
≥ λ, where ∞ represents the non allowed
assignments.
2.4 Gating
In order to eliminate the unlikely correspondence and
to reduce the number of candidate we use the Gating
technique (Blackman and Popoli, 1999) (Bar-Shalom
and Blair, 2000). A gate is formed about the predicted
track position and all detected objects falling within
the gate are assumed to be potential candidates for as-
sociation with the given track. The value of the cost
matrix between the track with the other detected ob-
jects which failed the gate test will be set to ∞. We
consider the gating approach proposed in (Blackman
and Popoli, 1999), where a track is said to satisfy the
gate of a given track if the residual vector
˜
y, with
residual matrix s
k
= HP
k/k −1
H + R satisfy the rela-
tion:
|y − ˜y| ≤ 3σ (2)
where H is the measurement matrix, P
k
/k − 1 is
the covariance matrix, R is the noise covariance ma-
trix, σ =
q
σ
2
0
+ σ
2
p
is the residual standard deviation
of the measurement σ
0
and prediction σ
p
variances.
2.5 Track Description Model Update
To take into account the changes of the tracked ob-
ject over time, it is necessary to update the description
model according to target changes. Suppose that the
track T
k−1
j
with a description model Ψ
k−1
j
has been
assigned to the observed object Ob
k
i
which has a de-
scription model Ψ
k
i
, then the new description model
Ψ
k
j
of the track T
k
j
is calculated thanks to the follow-
ing relation (Nummiaro et al., 2003):
Ψ
k
j
= (1 − α)Ψ
k−1
j
+ αΨ
k
i
(3)
where α ∈ [0,1] weights the contribution of the ob-
served model. When α is small, the new model will
mainly depends on the old description model. This
case is suitable when there are no occlusions and
when the tracked object does not changes largely from
one frame to the next one. On the other hand, if α
is high, then the new description model will mainly
depends on the new observed description model;
this case is suitable when there are significant target
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
472

changes, under the condition that the similarity be-
tween description models was below the threshold λ.
In order to update the target description model auto-
matically the update step will be done according to
the confidence step (Muoz-Salinas et al., 2008). So
we set α = c
i, j
. It will be small when the similarity
between the description models of T
k−1
j
and Ob
k
i
is
high. It should be underlined that the update step ap-
plied only to the appearance model.
2.6 Track Management
Track management module deals with the life of a
track. It create new ones, delete tracks which exit the
image and maintain the others. For each track there
are four possible states:
• Track Initiation (TI). This case corresponds to
a new object entering in the scene. This process
follows two steps. For every new created track, it
will be firstly considered as a ”tentative” one. Be-
hind the track is reported as a ”confirmed” track.
Otherwise the ”tentative” track is expected to be
a false one and it will be deleted. This technique
has been used to filter out the unstable tracks and
false detection which has a low probability of be-
ing tracks over several images. A unique label
(a track number) is assigned for each confirmed
track.
• Track Association (TA). This is the case when
the new detected object is correctly associated to
a track. Thus this step enables to link detection
corresponding to the same object over successive
frames.
• Track Continuation (TC). This is the case when
the tracked object is not detected, partially or
completely occluded, or is miss associated. So
this case deals with partial trajectories. Any track
can be in such situation for a specific time dura-
tion τ. If there is no correspondence of this track
with any detected object after the threshold time
τ, then the track will be deleted as we expect that
the tracked object has left the scene.
• Track Termination (TT). This is the case when
the tracked objects leave the scene. The decision
to delete a track is typically based on an elapsed
time span τ over which no detection of that object
has been confirmed.
If the state of a track is TC, then only the Kalman
filter predicted position will be considered as the tar-
get position. The prediction is applied until the state
of the track changes, either to TT state where the track
will be deleted, or to TA state where the track will be
again associated to a new detected object.
Frame f
1
(N
1
= 3)
Ob
1
1
Ob
2
1
Ob
3
1
Frame f
2
(N
2
= 4)
Ob
1
2
Ob
2
2
Ob
3
2
Ob
4
2
Object Model
Feature vector descriptor
of Ob
2
1
Track Model
Feature vector descriptor of T
3
1
T
1
2
[TA]
T
4
2
[TI]
T
3
2
[TA]
T
5
2
[TI]
T
2
2
[TC]
T
1
1
[TI]
T
2
1
[TI]
T
3
1
[TI]
Figure 2: Example of track management task between two
frames, the state of each track is based on the assignment
problem.
Figure 2 shows an example of the track manage-
ment task between two frames. The figure shows the
state of each track which is based on the assignment
problem. To simplify the explanation, we suppose
that the number of consecutive frame needed to con-
firm detected tracks in this example is one frame. In
the initial frame f
1
there are three detected objects,
leading to three tracks created with a TI state. In the
second frame f
2
, four objects are detected two of them
being new. Five tracks result from the second frame,
two tracks with a TI state, two tracks with a TA state,
and one track with a TC state. Table 1 shows a hy-
pothetical cost matrix based on this example. Within
this table the columns represent the detected objects
while the rows correspond to the tracks. From the ta-
ble, we may note the following:
• Ob
k
∗
i
represents a hidden object, i.e. the tracked
object is not detected in the new frame. If a track
is assigned to this case, then the state of this track
will be TC. For each track in this state there will
be a time stamp t indicating the duration time of
this track within this state.
• T
k
∗
j
represents the creation of a new track. If the
detected object is assigned to this case, then the
state of the corresponding track will be TI.
• c
TC
represents the cost of a track continuation be-
tween the selected track and object, which is given
as:
c
TC
i, j
=
λ if t
i, j
≤ τ and i = j
∞ otherwise
(4)
where t
i, j
is the time duration of the track j within
TC state.
If a track cannot be associated to any object in a
visible or hidden state, in other words if all the asso-
ciation cost of the corresponding row are infinite, the
track is terminated.
Given the set of costs C
k
and the assignment ma-
trix A
k
, subject to the uniqueness, the objective is to
TRACKING MULTIPLE TARGETS BASED ON STEREO VISION
473

Table 1: Cost matrix for the situation depicted in figure 2.
Objects
Tracks Ob
2
1
Ob
2
2
Ob
2
3
Ob
2
4
Ob
2
∗
1
Ob
2
∗
2
Ob
2
∗
3
T
1
1
c
1,1
c
2,1
c
3,1
c
4,1
c
T,C
∞ ∞
T
1
2
c
1,2
c
2,2
c
3,2
c
4,2
∞ c
T,C
∞
T
1
3
c
1,3
c
2,3
c
3,3
c
4,3
∞ ∞ c
T,C
T
1
∗
1
λ ∞ ∞ ∞ ∞ ∞ ∞
T
1
∗
2
∞ λ ∞ ∞ ∞ ∞ ∞
T
1
∗
3
∞ ∞ λ ∞ ∞ ∞ ∞
T
1
∗
4
∞ ∞ ∞ λ ∞ ∞ ∞
Table 2: Assignment matrix for the situation depicted in
figure 2.
Objects
Tracks Ob
2
1
Ob
2
2
Ob
2
3
Ob
2
4
Ob
2
∗
1
Ob
2
∗
2
Ob
2
∗
3
T
1
1
1 0 0 0 0 0 0
T
1
2
0 0 0 0 0 1 0
T
1
3
0 0 1 0 0 0 0
T
1
∗
1
0 0 0 0 0 0 0
T
1
∗
2
0 1 0 0 0 0 0
T
1
∗
3
0 0 0 0 0 0 0
T
1
∗
4
0 0 0 1 0 0 0
find the optimal assignment. That means the assign-
ment which minimize the total cost. This is an assign-
ment problem which can be solved by several meth-
ods such as the Nearest Neighbour (NN), the Global
Nearest Neighbour (GNN) or the Hungarian method.
We consider here a simple variant of the widely used
approach, the GNN (Blackman and Popoli, 1999)
which maintains the single most likely hypothesis. To
handle conflicting associations, a search is made for
the global minimum cost of the cost matrix, with the
condition that a
i, j
= 1. The elements of the cost ma-
trix in the same column or the same row were set ∞.
The process is repeated with the next global minimum
cost, until all the correspondence associations have
been made. Table 2 shows the optimal solution for
the example in figure 2.
Finally, We have to note that when the state of the
track changed to the state TC, the track keeps the last
model, i.e. Ψ
k
j
= Ψ
k−1
j
.
3 EVALUATION FRAMEWORK
Evaluating tracking algorithms performance is an
important stage for improving tracking techniques
(Brown et al., 2005). For the multiobject tracking
problem no standard metrics are available which can
solve the challenging problems of the varying num-
ber of targets and the complex occlusions in order to
obtain exact performance evaluation of the tracking
problem.
To evaluate the tracking algorithms, there are two
general ways: the visual analysis and the quantitative
evaluation. A visual analysis of the test sequences
gives a general overview of the tracker performance.
On the other hand, quantitative analysis used to mea-
sure the performance. This section is related to the
quantitative analysis, while the visual analysis will be
studied in the next section. Two approaches are con-
sidered here to evaluate the tracking result quantita-
tively, the confidence measure and the percentage of
correct matching.
3.1 Confidence Measure
The confidence measure indicates the degree of con-
fidence on the tracking result. We propose to use the
association cost c
i, j
as a confidence measure. There-
fore, the cost is normalized between 0 and 1 :
CM
i, j
=
c
i, j
+ 1
2
(5)
Ideally, when CM = 1 the description models are
identical. But in reality, it will be lower than the max-
imum value due to partial occlusions or target defor-
mation. The advantage of this measure is that there
is no need to have a ground truth for the quantitative
evaluation of tracking result. The confidence measure
of a frame is defined as the average of the confidence
measures of all tracks in the frame.
3.2 The Percentage of Correct Matching
The Percentage of Correct Matching PCM, is another
measure used to evaluate quantitatively the tracking
performance. This technique is similar to the one pro-
posed in (Scharstein and Szeliski, 2002) for evaluat-
ing stereo algorithms. In our case, this measure, rep-
resented as PCM
k
, corresponds to the percentage of
the correct correspondence compared to the total cor-
respondence between the frames f
k−1
and f
k
. Figure 3
shows an example of calculating the PCM
2
between
the frames f
2
and f
1
. We defined also the measure
PCM for a sequence as the average percentage of cor-
rect matching of the the processed frames.
4 EXPERIMENTAL RESULTS
In this section, experiments that have been conducted
to illustrate the performance of the proposed track-
ing algorithms is presented. As already mentioned,
the proposed method was applied in the context of
pedestrian protection. The performance of the pro-
posed technique is illustrated on two real image se-
quences depicting crowded scenes taken from an on
board stereo system. These sequences were chosen to
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
474
Frame f
1
N
1
= 4
Ob
1
1
Ob
2
1
Ob
3
1
Frame f
2
N
2
= 5
Ob
1
2
Ob
2
2
Ob
4
2
Ob
4
1
Ob
5
2
Ob
3
2
PCM
2
= ¾ = 75%
Figure 3: Example of calculating the Percentage of Correct
Matching between f
1
and f
2
.
contain challenging groups of people walking in mul-
tiple directions with significant occlusions, and com-
plex background. The first sequence consists of about
200 frames while the second consists of about 300
frames both with an image resolution of 640 × 480
pixels. The number of consecutive frames needed to
confirm detected tracks in the following examples was
set to three frames. The threshold λ on the cost func-
tion was set to 0.2 for all experiments.
In the first sequence the algorithm is tested against
a manually labeled ground truth: a bounding box en-
closing each target was drawn and the ground plane
position was computed from stereovision data.
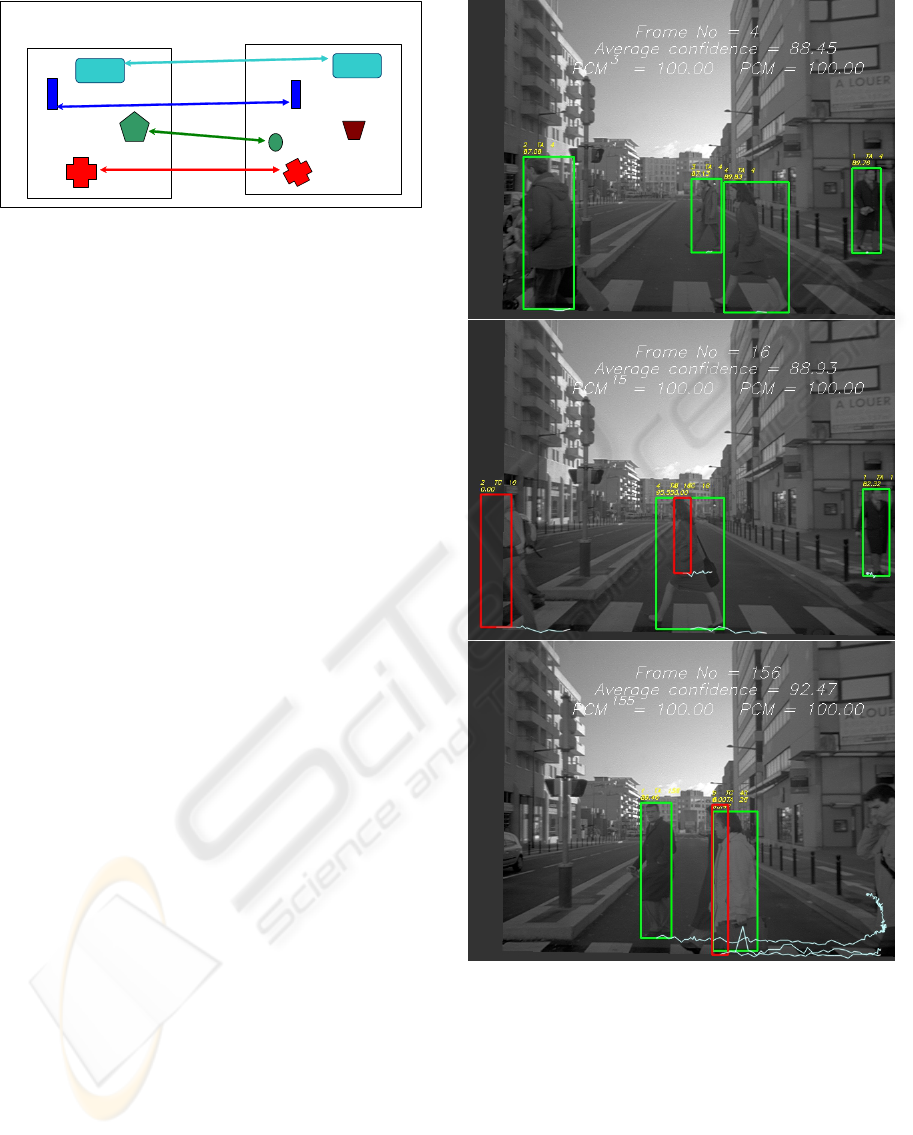
Samples of the tracking results shown on the right
camera images can be seen in Figure 4. The trajec-
tories of each target from the actual position of the
bounding box to previous positions is also displayed.
The position of each target is represented by a point
on the ground, i.e. in the center of the lower part of
the target bounding box.
For each frame, the system shows the evaluation
of the tracking result, i.e. the average confidence mea-
sure and the PCM. Also near each target there are lo-
cal results such as target number (i.e. target label),
target state (TI, TA, TC), number of frames this target
has been tracked, the confidence measure of the track-
ing result of the target and the trajectory of the target.
From Figure 4, we can note that the system correctly
tracks each target despite complete occlusions (as for
the target 3 in frame 16) and shape deformations. The
PCM is equal 100% for all the frames indicates that
the tracking result is fully coherent with the ground
truth.
The samples results presented in Figure 5 shows
the tracking results on a second sequence. The visual
analysis of Figure 5 reveals the following facts:
• During this sequence, some close targets are con-
sidered as a single target, so it is difficult to track
them individually.
• The bounding boxes for each target have some in-
stabilities.
Figure 4: Tracking results with ground truth detection. The
confidence measure is expressed as a percentage. The three
images correspond to frames 4, 16, 155. Bounding box
color correspond to the state of the track: green for TA and
red for TC.
• There are some detection errors, such as false de-
tections.
All these errors have a negative influence on the
tracking result as indicated in the confidence measure.
In fact, many errors can be explained by the complex
crowded conditions, and the problem of the descrip-
TRACKING MULTIPLE TARGETS BASED ON STEREO VISION
475

Figure 5: Tracking results with stereo detection. The three
images correspond to frames 50, 75, 88. Bounding box
color correspond to the state of the track: green for TA and
red for TC.
tion model. The tracker is successful for the first 76
frames. Each track keeps its own label and the false
detections are filtered out. However, it begins to en-
counter difficulties in frame 77 as it passes a com-
plex occlusions. It is worthy to point out the results
in frame 77 where the object with track number 1 is
miss associated to track 3 (see also Figure 6 ). There
are other problems arising when the duration of the
target in the TC state is greater than the time span τ.
In this case the tracker will create a new track for the
target (track 5 in frame 88). This sort of failure is
quite natural and should be expected, it can be mini-
mized by the better selection of the parameters of the
tracker: the noise parameters in the Kalman filter, the
threshold λ on the cost function, and the cost function
itself.
−2.5 −2 −1.5 −1 −0.5 0 0.5 1 1.5 2 2.5
3.5
4
4.5
5
5.5
6
6.5
7
7.5
X Position
Z Position
Object=1
Object=2
Object=3
Object=5
Figure 6: Trajectories of each tracked object on the (X,Z)
ground plane for the second sequence. The red lines cor-
respond to the trajectories corrected by the Kalman filter.
The blue points represent the measurement provided by the
stereovision detection algorithm.
As expected, the tracking result is not perfect for
this example. However, the system generally tracks
all targets with acceptable accuracy.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we have presented a stereo vision based
tracker that is able to track multiple objects in outdoor
scenarios. The proposed technique is able to deal with
multiple targets and invalid observations in cluttered
environments, enabling us to reconstruct the 3D tra-
jectories and estimate the speed of detected objects.
Furthermore, to assess the tracking quality, the perfor-
mance of the tracker was estimated using confidence
measure and the percentage of correct matching. Two
sets of tracking results are illustrate the performance
of the algorithm on real data. The system is able to
process each frames in about 180 ms on a standard
PC (2GHz, 1Go) . Experimental results also show
also the quality of the tracking results depends on the
results of the detection algorithm.
Future research will focus on: optimizing the tech-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
476

nique to obtain real time tracking, tracking of clut-
tered objects, study the effect of nonlinear prediction
on the tracker performance, and study the correla-
tion between GT and Confidence Measure for perfor-
mance evaluation.
ACKNOWLEDGEMENTS
This work is part of the LOVe Project funded by the
“Agence National de la Recherche” (ANR).
REFERENCES
Bar-Shalom, Y. and Blair, W. (2000). Multitarget-
Multisensor Tracking: Applications and Advances,
volume III. Artech House, Norwood, MA.
Blackman, S. and Popoli, R. (1999). Modern Tracking Sys-
tems. Artech House Publishers Library, 2nd edition.
Brown, L., Senior, A., Tian, Y.-L., Connell, J., and Ham-
papur, A. (2005). Performance evaluation of surveil-
lance systems under varying conditions. In IEEE Int’l
Workshop on Performance Evaluation of Tracking and
Surveillance.
Cox, I. and Hingorani, S. (1996). An efficient implemen-
tation of reid’s multiple hypothesis tracking algorithm
and its evaluation for the purpose of visual tracking.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 18(2):138–150.
Fortmann, T., Bar-Shalom, Y., and Scheffe, M. (1983).
Sonar tracking of multiple targets using joint prob-
abilistic data association. IEEE Journal of Oceanic
Engineering, 8(3):173–184.
Gavrila, D. and Munder, S. (2007). Multi-cue pedestrian
detection and tracking from a moving vehicle. Inter-
national Journal of Computer Vision, 73(1):41–59.
Labayrade, R., Aubert, D., and Tarel, J.-P. (2002). Real
time obstacle detection in stereovision on non flat road
geometry through ”v-disparity” representation. IEEE
Intelligent Vehicle Symposium, 2:646–651.
Medioni, G., Cohen, I., Bremond, F., Hongeng, S., and
Nevatia, R. (2001). Event detection and analysis from
video streams. IEEE Transactions on Pattern Analy-
sis and Machine Intelligence, 23(8):873–889. 0162-
8828.
Muoz-Salinas, R., Aguirre, E., Garca-Silvente, M., and
Gonzalez, A. (2008). A multiple object tracking ap-
proach that combines colour and depth information
using a confidence measure. Pattern Recognition Let-
ters, 29(10):1504–1514.
Nummiaro, K., Koller-Meier, E., and Van Gool, L. (2003).
An adaptive color-based particle filter. Image and Vi-
sion Computing, 21(1):99–110.
Rasmussen, C. and Hager, G. (2001). Probabilistic data as-
sociation methods for tracking complex visual objects.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 23(6):560–576.
Reid, D. (1979). An algorithm for tracking multiple targets.
IEEE Transactions on Automatic Control, 24(6):843–
854.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. International Journal of Computer Vision,
47(1):7–42.
TRACKING MULTIPLE TARGETS BASED ON STEREO VISION
477
