TESSELLATING ALGEBRAIC CURVES AND SURFACES

USING A-PATCHES

Curtis Luk and Stephen Mann

University of Waterloo, 200 University Ave W., Waterloo, Ontario, Canada

Keywords:

Algebraic surfaces, A-patches, Tesselation.

Abstract:

This work approaches the problem of triangulating algebraic curves and surfaces with a subdivision-style algo-

rithm using A-patches. An algebraic curve or surface is converted from the monomial basis to the Bernstein-

Bezier basis over a simplex. If the coefﬁcients are all positive or all negative, then the curve or surface does

not pass through the domain simplex. If the scalar Bernstein coefﬁcients are of mixed sign and have a layer

separating the positive from the negative, then the patch is in A-patch format and can be efﬁciently tessellated.

Cases of mixed sign without a separating layer are resolved by subdividing the structure into a set of smaller

patches and repeating the algorithm.

Using A-patches to generate a tessellation of the surface has the advantage of reducing the amount of subdi-

vision required. And because of the A-patch properties, we are guaranteed that features within the designated

region will not be missed.

1 INTRODUCTION

With modern graphics cards, it is possible to render

implicit surfaces directly on the GPU without tessel-

lating them. However, tessellation is still one viable

method of rendering implicit surfaces, and fast, ac-

curate methods of tessellation remain important. One

prevalent method of triangulating implicit surfaces in-

volves the use of subdivision, which is the process

of dividing space into regions that can be recursively

split into increasingly smaller regions.

There are several advantages in using A-Patches

to construct a triangular approximation of an alge-

braic surface, which are the ease in which A-Patches

can be evaluated for low degree polynomials and the

ease in which points on the surface can be found

within an area that is in A-Patch form. Most im-

portantly, it can be shown that a domain that con-

forms to speciﬁc A-Patch conﬁgurations has a small

number of single-sheeted orientations that can exist

within the patch. This removes various ambiguities

that could pose problems when evaluating complex

surfaces, such as self-intersections and singularities.

Some subdivision algorithms require subdomains

to be highly subdivided to generate a tessellation with

a high sampling rate, which is used to generate a high

quality surface approximation. The A-Patch method

can ﬁnely tessellate surfaces with less use of repeated

recursive subdivision of the target space. More impor-

tantly, our method will not misclassify multisheeted

regions as having a single sheet, nor will it miss small,

disconnected components within the region of inter-

est.

1.1 Background

An implicit surface in 3-space is the set of all points

where F(x,y,z) = 0. If F is polynomial, then the sur-

face is said to be algebraic. The problem of tessel-

lating an implicit surface has been tackled in the past,

and such schemes can be classiﬁed in one of several

categories. Subdivision schemes such as Marching

Cubes (Lorensen and Cline, 1987) attempt to ﬁnd a

polygonalization of an implicit surface by dividing

the space into a three dimensional grid. The grid cells

are further divided to smaller components. This class

of algorithm can make the surface extremely costly to

evaluate at areas of high precision.

Ray casting is another method to generate a polyg-

onalization of an algebraic surface, which is done by

ﬁnding intersections between lines projected from an

origin point and the surface. Although ray casting can

tessellate a surface to any arbitrary degree of precision

by casting an increasing number of rays, it must rely

Luk C. and Mann S. (2009).

TESSELLATING ALGEBRAIC CURVES AND SURFACES USING A-PATCHES.

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 82-89

DOI: 10.5220/0001790400820089

 SciTePress

on alternate methods for detecting anomalies such as

self-intersections and singularities. Also, although the

method can sample an arbitrary number of points on

the surface, ray casting cannot infer the topology of

the surface without using a point cloud surface con-

struction algorithm (Wang et al., 2005).

There exists another class of approximating alge-

braic surfaces using piecewise parametric surfaces.

Bajaj and Xu propose one such technique (Bajaj and

Xu, 1997), with parametric surface patches being

grown around pre-computed seed singularities. This

method provides the advantage of generating a para-

metric representation of the surface (as opposed to

a piecewise linear approximation) of the surface, al-

though the process involved requires several major

steps, including computation of the singularities, di-

rect triangulation, and ﬁtting parametric patches over

the triangulation. On the other hand, Jepp, van

Overveld, Wyvill, and Wyvill (Wyvill et al., 2000)

propose a method combining marching cubes with

subdivision surfaces to approximate an implicit sur-

face. This method is capable of generating approxi-

mations at real-time speeds, but the accuracy of the

surface in relation to the deﬁned algebraic surface is

sacriﬁced as a result.

1.2 Previous Work

The concept of the trivariate Bernstein-B

ezier basis

representation within a tetrahedral volume is not new.

Sederberg (Sederberg, 1985) deﬁnes such a structure,

which he calls an algebraic surface patch, as a tool

for modeling free form algebraic surfaces due to its

ability to deﬁne a wide variety of surfaces with a

low degree compared to parametric surfaces and since

they inherently deﬁne half-spaces, which is useful for

modeling solid geometry. Bajaj (Bajaj and Ihm, 1992)

proposed using A-patches for ﬁtting surface data and

later (Bajaj et al., 1995) proposed a method of build-

ing models using piecewise A-patches. Speciﬁcally,

a set of A-patches is used to construct models that

are C

continuous and match the topology of the orig-

inal model speciﬁcation. A-patches were also pro-

posed for constructing algebraic surfaces (Bajaj and

Xu, 1997), although unlike the method presented here

it uses the patches as spline surfaces that approximate

the algebraic surface as opposed to using A-patch

properties to compute points on the surface.

The use of subdivision algorithms for tessellating

algebraic surfaces is not a recent phenomenon, with

Bloomenthal (Bloomenthal, 1988) proposing a tes-

sellation method that relies on repeated subdivision

of a domain space and surface-line intersection eval-

uation. Further, more recent work on subdivision-

style polygonalization algorithms have been pursued

by Belyaev and Ohtake (Ohtake and Belyaev, 2002)

on implicit surfaces with sharp features. Unlike pre-

vious subdivision methods, our A-patch scheme relies

on the tetrahedron as opposed to the cube as a unit

space. This is due to the geometric requirements dic-

tated by the structure of the A-patch, although subdi-

viding a tetrahedron is a more difﬁcult task than sub-

dividing a cube.

This paper will investigate both the theoretical and

implementation aspects of the basic A-patch surface

approximation method. We begin with a review of

A-patches, after which we present an algorithm for

ﬁnding a piecewise linear approximation to a 2D al-

gebraic curve. We then generalize the algorithm to

tessellate algebraic surfaces in 3D.

2 A-patch BASICS

An algebraic surface patch (also known as an A-

patch) is essentially a piece of an algebraic surface

that is constrained within an arbitrary tetrahedron.

The contour of the surface contained within the tetra-

hedron is determined by the weight of its control

points. In A-patch form, the algebraic surface is rep-

resented in the Bernstein-B

ezier basis. Normally, al-

gebraics are represented as a vector of scalars that cor-

responds to the monomial basis

(P) = x

where 0 ≤ a, b,c and a + b + c = n. The Bernstein-

ezier basis in three-space is

(P) =





where

i = (i

) with 0 ≤ i

and i

+ i

= n and where p

, p

are the

Barycentric coordinates of P relative to a domain

tetrahedron T = 4ABCD. The A-patch uses the

Bernstein-B

ezier basis to weigh scalar values in the

following relationship:

F(P) =

∑

(P).

The scalar coefﬁcients C

(also called control points)

have no location in the space we are interested in, al-

though one can imagine them to be distributed evenly

across the triangular domain as Bernstein/B

ezier con-

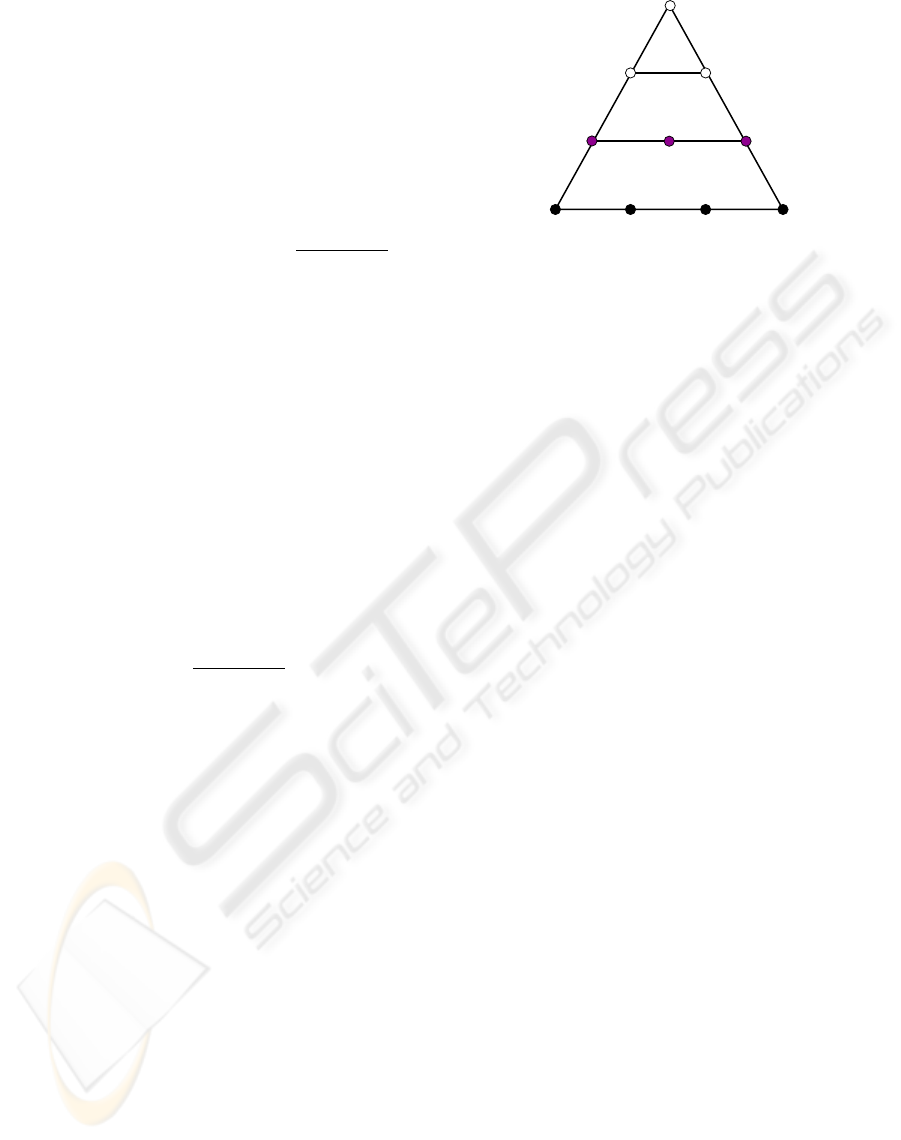
trol points of the patch as seen in Figure 1; this visual-

ization will be particularly helpful when talking about

the separating layer of control points in the later sec-

tions of this paper. For a Bernstein/B

ezier represen-

tation to be an A-patch, its coefﬁcients must satisfy

TESSELLATING ALGEBRAIC CURVES AND SURFACES USING A-PATCHES

0020

0110

0200

1010

0011

011

020

110

002

200

101

1100

1001

2000

0002

Figure 1: Visualizing the B

ezier coefﬁcients in the domain.

certain conditions on their signs, as we will discuss in

Sections 4 and 5.

The two dimensional representation of a polyno-

mial curve in monomial form is similar to its three

dimensional surface counterpart. The only difference

is that there is one less variable. This means that the

monomial basis becomes

(P) = x

where 0 ≤ a, b and a+b = n. The bivariate Bernstein-

ezier basis is

(P) =





where

i = (i

) with 0 ≤ i

and i

n and where p

, p

, and p

are the Barycentric coor-

dinates of P relative to a domain triangle T = 4ABC.

Standard change of basis algorithms can be used

to convert between the monomial and Bernstein repre-

sentations. Evaluating the algebraic function in Bern-

stein form at a point in the region can be accom-

plished by performing a de Casteljau evaluation of the

A-patch. de Casteljau’s algorithm also subdivides a

curve into two sets of control points, each of which

is the representation for the curve over a subdomain

determined by the evaluation point. de Casteljau’s al-

gorithm can also subdivide higher order B

ezier func-

tions, although these methods become more complex

as the dimension increases. For details on Bernstein-

ezier representations, change of bases, and subdivi-

sion algorithms, see (Farin, 2002).

2.1 Conditional A-patches and

Application

A-patches have six characteristics that are deﬁned

by Sederberg in his paper regarding algebraic sur-

face patches (Sederberg, 1985). These come into

play when we devise methods to generate tessella-

tions from A-patches. We list the two properties that

are most important for our purposes:

Point Interpolation Property. F(P) at any of the

tetrahedral vertices corresponds to the weight of the

control point at that vertex.

Line Interpolation Property. If the weights of all

the control points along an edge are zero, then the

edge interpolates the surface F(P) = 0.

More importantly, Sederberg (Sederberg, 1985)

(Sederberg and Anderson, 1985) and Guo (Guo,

1995) showed that if monotonicity conditions hold

on edge lines of a tetrahedron then all parallel lines

will intersect the algebraic surface at most once. Ba-

jaj (Bajaj et al., 1995) elaborates on this by formaliz-

ing the concept of the three-sided and four-sided al-

gebraic patch, both of which are shown to be single-

sheeted and non-singular. In addition, the algebraic

patches Bajaj propose do not require the monotonic

conditions outlined by Sederberg, and instead impose

restrictions on the signs of the coefﬁcients.

We restate Bajaj’s deﬁnition of three and four-

sided A-patches:

Deﬁnition: Three-sided Patch. Let the surface

patch S

be smooth on the boundary of the tetra-

hedron T = 4e

. If any open line segment

,α∗) with α∗ ∈ S

= {(α

,α

)

: α

0,α

> 0,

∑

i6= j

= 1} intersects S

at most once

(counting multiplicities), then we call S

a three-sided

j-patch.

Deﬁnition: Four-sided Patch. Let the surface

patch S

be smooth on the boundary of the tetrahe-

dron T = 4e

). Let (i, j,k,l) be a permutation

of (1, 2,3,4). If any open line segment (α∗, β∗) with

α∗ ∈ (e

) and β∗ ∈ (e

) intersects S

at most once

(counting multiplicities), then we call S

a four-sided

i j-kl-patch.

Using the above information we can generate

approximations of surfaces and curves with three

and four-sided A-patches and their two dimensional

equivalent. To ﬁnd this using just the Bernstein co-

efﬁcients and the domain tetrahedron, we must ﬁnd a

set of edge points whose weights have opposite signs.

From there we can ﬁnd the point between the pairs

where F(P) = 0. Sections 4 and 5 will elaborate on

the basic outline provided here.

3 THEOREMS

From the basic properties of A-patches we can de-

rive a number of theorems that will be relevant to the

A-patch tessellation algorithm. Although Bajaj states

conditions for a single-sheeted surface, we must also

determine regions that do not contain the surface. The

following theorems justify the method to ﬁnd these

regions by ﬁnite subdivision of the region and inves-

tigation of the coefﬁcients of the empty regions.

Theorem 1: Given a d dimensional simplex T =

.. .V

and a dimension d, degree n polynomial

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

F with Bernstein coefﬁcients C

over T , if C

> 0 for

all

i then F(p) > 0 for all p ∈ T .

Proof: This follows immediately from the Bern-

stein basis functions forming a convex combination

over T .

Theorem 2: Given a dimension d, degree n alge-

braic function F whose value is strictly greater than

ε > 0 on the interior of a simplex T and where the

Bernstein representation of F over T has coefﬁcients

of mixed sign. Then over any aligned subsimplex T

of T with edge lengths no greater than

d−N(2d+2)

/εe

the size of those of T , the Bernstein coefﬁcients of F

over T

are all non-negative, where N < 0 is the most

negative Bernstein coefﬁcient of F represented over

T .

Proof Sketch: The proof proceeds by considering

an arbitrary, aligned subsimplex whose edges are half

the length of the initial simplex. We can show that the

most negative coefﬁcient of the subsimplex will be at

least a ﬁxed amount larger than the most negative co-

efﬁcient of the initial simplex, where the ﬁxed amount

is dependent on ε, d, and n (i.e., it is independent of

the Bernstein coefﬁcients). From here, we just ﬁnd

the number of “halvings” needed to ensure that all the

Bernstein coefﬁcients are positive. See (Luk, 2008)

for details.

Lemma 3: For any set of simplices covering T

where each simplex can be embedded in an aligned

subsimplex of T of size

d−N(2d+2)

/εe

then the Bern-

stein coefﬁcients of F over each subsimplex will be

non-negative.

Proof: The lemma follows immediately from the

Theorem 2.

Comments: The theorems and lemmas also hold

for F(p) < 0, F(p) < ε < 0, etc. Also note that

Lemma 3 is a very loose bound on the number of sub-

divisions needed to have all the coefﬁcients be of one

sign when working in a region where F(p) > 0; in

general, we expect (and observed) much faster con-

vergence than this. While Theorem 1 is a well known

simple observation, Theorem 2 and Lemma 3 are new

and are a specialized generalization of the property

that the B

ezier curve control polygon converges to the

curve under repeated subdivision.

4 APPROXIMATING ALGEBRAIC

CURVES

We begin by presenting a method for ﬁnding a piece-

wise linear approximation to a 2D algebraic curve.

We assume that the user has selected a region of in-

terest, and that this region has been triangulated. We

Figure 2: A possible separating layer in an ideal two-

pointed A-patch. The white have negative sign; the black

have positive sign; the magenta is the separating layer, and

the coefﬁcients may have either sign.

then ﬁnd the Bernstein representation for the alge-

braic function over each triangle.

After converting to Bernstein-B

ezier format, it is

necessary to determine whether each triangle contains

the curve. This can be determined by examining the

sign of the Bernstein coefﬁcients. If all the coefﬁ-

cients of a triangle are non-zero and of one sign, then

the curve does not pass through the triangle (Theorem

1), and the triangle need no longer be considered.

Triangles with Bernstein-B

ezier coefﬁcients of

mixed sign can be categorized into two different

classes. The ﬁrst is what we will refer to as a two-

pointed A-patch. For a Bernstein representation to

be a two-pointed A-patch with domain triangle T =

4ABC, there must exist a vertex control point (as-

sume it is A for discussion) such that F(A) does not

have the same sign as F(B) and F(C). In addition,

there must exist a layer of mixed-sign control points

that separates a set of positive control points from a

set of negative control points, illustrated in Figure 2.

See (Bajaj and Xu, 1997) for a more formal deﬁnition

of an A-patch.

If the Bernstein representation is a two-pointed

A-patch, then the curve can be approximated within

the domain of the patch as described in the next sec-

tion. Otherwise, we will perform a 4-to-1 subdivision

of the triangle. The control points of the four new

patches are computed and the search for a separating

layer is performed on each subtriangle.

In our implementation, we used a 4-to-1 subdi-

vision (B

ohm, 1983); however, a 2-to-1 subdivision

would produced similar results and would be easier

to implement (Peters, 1994).

4.1 Approximating the Curve

Let 4ABC be the domain for a two-pointed A-patch

F with a separating layer. In this situation, two of

the corner B

ezier coefﬁcients will have one sign (e.g.,

TESSELLATING ALGEBRAIC CURVES AND SURFACES USING A-PATCHES

Figure 3: Curve properties that are not present in an A-patch

with a separating layer.

F(A) > 0 and F(B) > 0), and the third coefﬁcient

(e.g., F(C) < 0) will have the opposite sign. Be-

cause of the separating property, the algebraic func-

tion’s value at any point on the edge AB will have the

same sign as F(A) and F(B). We will sample AB for

a sequence of points, P

,. .., P

, and for each point

, we consider the line between it and C.

Again, because of the separating layer, there is

one zero of F along the line segment P

C. A nu-

merical search can quickly ﬁnd this zero. Our piece-

wise linear approximation to the curve in this region

is made by connecting this sequence points at which

F is zero. The single-sheeted properties of the patch

will guarantee that by interpolating from one vertex to

the other we do not need to consider certain features,

such as those seen in Figure 3.

Figure 4 shows some examples of implicit curves

evaluated in this manner. Lemma 3 ensures that we

will eventually stop subdividing in regions that do not

contain the curve. However, if there is a singularity

in the curve, an A-patch over any triangular region

containing this singularity will not have a separating

layer. As the algorithm reﬁnes in this region, the sin-

gularity will become more and more localized, but if

the precise location of the singularity is desired, an-

other method must be used to ﬁnd it.

Figure 5 shows the subdivision of space of a curve

that has a singularity. Notice the increasing depth of

subdivision near the singularity. Also note that sub-

division stops fairly quickly in regions not containing

the curve, and that away from the singularity, the tri-

angles were in A-patch format at a fairly coarse level,

even if the curve just clipped a triangle or if the curve

passed through the triangle at unusual angles.

5 TESSELLATING ALGEBRAIC

SURFACES

We now consider algebraic surfaces. To improve

computational efﬁciency of the surface construction

algorithm it is essential to have a good subdivision

scheme. Unfortunately, unlike triangles the regular

tetrahedron cannot be constructed from a small num-

ber of regular tetrahedra, which makes both subdivi-

sion and tetrahedron layout non-trivial problems. We

chose to abandon the use of regular tetrahedra and

worked with axis-aligned grids of cubes, with each

cube containing a set of tetrahedra instead. The use

of axis-aligned cubes has advantages in making the

structure easier to understand and implement, as well

as accommodating a reasonable subdivision scheme.

We considered two schemes for A-patch layout

and subdivision based on the axis-aligned cube. The

ﬁrst method is deﬁned by dividing the cube into ﬁve

separate tetrahedron, shown in Figure 7, left. This ar-

rangement results in a cube that is created with a mini-

mum number of A-patches. Unfortunately, in this lay-

out adjacent cubes must be placed in a speciﬁc way

such that the faces of each A-patch are shared with

its neighbour otherwise tearing artifacts will appear

when the ﬁnal result is rendered.

The second method divides the cube into twelve

tetrahedron, outlined in Figure 7, right. This conﬁgu-

ration has a couple of advantages, the ﬁrst being that

the faces of every patch along the face of a cube match

perfectly with the faces of an adjacent cube’s patches,

provided that all the cubes follow the same A-patch

layout. A second advantage is that the tetrahedron

within the cube are of the same size and shape. Fi-

nally unlike the previous method there is no require-

ment for the cubes to be arranged in an octet to guar-

antee that the patch faces match up, which simpliﬁes

the implementation. Unfortunately this method also

yields over twice the number of patches than the 5-

patch cube over the same domain, which slows down

the algorithm by a corresponding amount. Due to the

decrease in the number of A-patch computations we

decided to use the ﬁrst method in the ﬁnal implemen-

tation.

5.1 Criteria for Subdivision and

Evaluation

As with the evaluation of two dimensional A-patches

we must determine whether or not the function lies

within the domain. Again, by analyzing the pattern

of the control points in the patch we can infer various

characteristics about it.

A-patches with mixed-sign control points fall un-

der one of three categories, two of which are suitable

for evaluation. The two ideal patches are outlined

by Bajaj (Bajaj and Xu, 1997), which he refers to

as three-sided and four-sided A-patches. Both three

and four-sided A-patches contain a separating layer

of control points similar to that found in the two-

dimensional case, although in this instance the con-

trol points extend in an extra dimension. Three-sided

A-patches contain one vertex control point that has

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

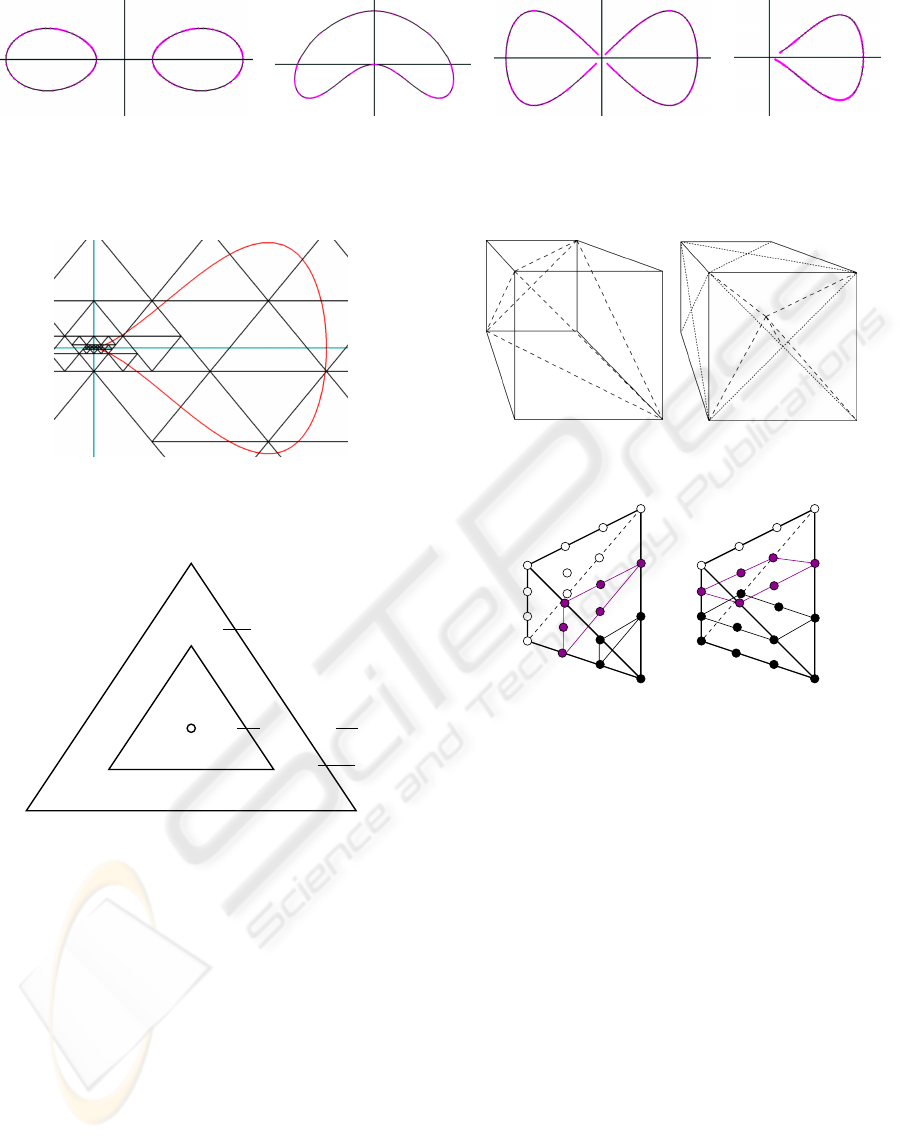
Figure 4: Curve approximations generated by the implementation. From upper left clockwise: x

+3x

+2y

−2x

+3y

0.2 = 0, x

+ 4x

y − 3x

+ 3y

− 4y = 0, x

− 2x

+ 2y

= 0, and 2x

− 2x

− y

= 0. The right two examples show

functions that have areas that cannot be approximated exactly at the point of the singularity.

Figure 5: Subdivision near a singularity.

2(d+1)

+ ...

d+2

2d+2

+ ...

C =

d+1

+ ... +

d+1

Figure 6: Variations in curve detail for A-patches containing

the input function.

a different sign than the other three while four-sided

patches contain two pairs of vertex control points that

have different signs from each other. Figure 8 shows

an example of separating layers for three and four-

sided A-patches. Note that three-sided A-patches

contain triangular-shaped surfaces while four-sided

A-patches contain quadrilateral-shaped surfaces.

If all the tetrahedron within a cube have entirely

positive or negative control points and/or passes the

three or four-sided A-patch criteria then it is possible

to approximate the surface that passes through the cu-

bic area using the method outlined in the next section.

Otherwise we subdivide the cube into eight separate

cubes. New Bernstein representations are computed

for the tetrahedrons in the subdivided cubes, and the

Figure 7: A diagram of an axis-aligned cube containing ﬁve

and twelve A-patches.

Figure 8: The separating layer of control points in a three

and four-sided A-patch. The white have negative sign; the

black have positive sign; the magenta is the separating layer,

and the coefﬁcients may have either sign.

process is repeated until all the patches are in the de-

sired conﬁguration. This may require multiple levels

of subdivision.

5.2 Tessellating the Surface

Once we have determined which tetrahedron are A-

patches, we can generate a piecewise linear approxi-

mation of the surface. We will use the same method

to determine a zero-set of the implicit function within

the domain of the patch as before, although the

method for evaluating the surface differs between a

three and four-sided patch. The main difference be-

tween the two situations lies in the number of points

to evaluate and the method in which pivoting points

are selected for ﬁnding a particular member of the

zero-set.

In the case of a three-sided patch, we know that

F has one sign at three of the corners of the domain

TESSELLATING ALGEBRAIC CURVES AND SURFACES USING A-PATCHES

C C

Figure 9: Tessellation of an A-patch: White points form

a triangular grid on a face/edge are of one sign; the black

point(s) has/have opposite sign. Red points are point on the

surface. Each red point is calculated by connecting a white

point to the black point and numerically searching for the

zero. The green line illustrates this for one point, with the

zero on the line being drawn in green rather than red.

tetrahedron T = 4ABCD, and the opposite sign at

the fourth corner. Assume that F has the same sign

at A,B,C. Since we have a separating arrangement of

control points, F has the same sign at all point on the

interior of 4ABC. We setup a triangular grid across

this face, and for each point P on the grid, we con-

struct a line to D. The separating arrangement of co-

efﬁcients ensure that F(P) and F(D) have opposite

signs, and further that there is exactly one zero on the

line segment PD. Again, we ﬁnd this zero by a nu-

merical search method.

Having found a zero of F corresponding to each

point on the triangular grid on triangle 4ABC, we

connect these zero points in the triangular arrange-

ment suggested by the triangular grid. This forms a

piecewise linear approximation to F over T .

In the four-sided patch case, things differ in that

two corners of T = 4ABCD have one sign (e.g.,

F(A) > 0, F(B) > 0), while the other two corners

have the opposite sign (e.g., F(C) < 0, F(d) < 0).

In this case, we uniformly sample both line segments

AB and CD, and form all connections between sam-

ple points on one edge to the sample points on the

other edge. Along each line segment, there will be

exactly one zero, which can be found with numeri-

cal search. The result will be a rectilinear grid that

approximates F over T . The tessellation algorithm

for both three and four-sided patches is illustrated in

Figure 9. Note that unlike the other ﬁgures, in this ﬁg-

ure the points are not representative of A-patch con-

trol points/coefﬁcients, but instead are actual points in

space.

Figure 10 show several surfaces that were approx-

imated using the implementation.

Note that as described, it is possible that the subdi-

vision of adjacent regions will be at different depths,

which can lead to a non-watertight boundary. This in

Figure 10: Planar and quadratic surface tessellations gen-

erated by the implementation. Clockwise from upper left:

−0.8 = 0, x+y+z+0.2 = 0, x

−z −0.8 =

0, and x

−y

−z −0.8 = 0. Magenta shows the tessellation.

Figure 11: A comparison between a standard and stitched

tessellation.

turn can lead to pixel drop-out. We implemented a

simple stitching scheme to address this problem (Fig-

ure 11) (Luk, 2008).

6 CONCLUSIONS

The A-patch method for approximating implicit

curves and surfaces is a sound one, both in theory and

in practice. The theorems outlined in the Section 3

demonstrate the convergence of the algorithm in do-

mains that do not contain the surface. But although

the theory guarantees that we can eventually decide

the surface does not exist in regions not containing

the surface, so far we have no guarantees that the al-

gorithm will ﬁnd A-patches for portions of the space

that do not contain singularities. However, our test

cases show the effectiveness of the method in ﬁnd-

ing a surface approximation in domains that contain

it, strongly suggesting that the method will converge

to A-patches for portions of the surface not near sin-

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

Figure 12: Approximating surface singularities to an arbi-

trary precision using A-patches. The orange box identities

an area with a high degree of subdivision.

gularities.

The big advantage of our algorithm is that for al-

gebraics, it avoids certain problems in tessellating im-

plicit surfaces. In particular, over the region of in-

terest, our algorithm is guaranteed not to misclassify

multiple sheets as a single sheet, nor will it miss small

disconnected features. Simplices containing such fea-

tures will not be in A-patch format, and the algorithm

will subdivide the region until the multiple sheets are

separated, the small disconnect components found, or

the maximal subdivision depth is reached (in which

case these regions are ﬂagged as special).

Like a vast majority of the algebraic approxima-

tion methods ours cannot properly identify the singu-

larities of the algebraic surface unless it is coincident

with a vertex control point of an A-patch. However,

even in the worst case the A-patch method is capable

of approximating a singularity point to an arbitrary

distance from the point of singularity via subdivision,

which gives us an unambiguous surface contour to

work on to complete the surface approximation ac-

curately. Figure 12 shows how repeated subdivision

of an algebraic surface with a singularity can gener-

ate an inﬁnitely close approximation of the singularity

without ever ﬁnding it.

REFERENCES

Bajaj, C. L., Chen, J., and Xu, G. (1995). Modeling with

cubic a-patches. ACM Transactions on Graphics, Vol-

ume 14, Issue 2, pages 103–133.

Bajaj, C. L. and Ihm, I. (1992). Algebraic surface de-

sign with hermite interpolation. ACM Transactions

on Graphics, Volume 11, Issue 1, pages 61–91.

Bajaj, C. L. and Xu, G. (1997). Spline approximations of

real algebraic surfaces. Journal of Symbolic Compu-

tation, Volume 23, Issue 2-3, pages 315–333.

Bloomenthal, J. (1988). Polygonization of implicit surfaces.

Computer Aided Geometric Design, 5(4):341–355.

ohm, W. (1983). Subdividing multivariate splines.

Computer-Aided Design, 15(6):345–352.

Farin, G. (2002). Curves and Surfaces for CAGD. Morgan-

Kauffmann.

Guo, B. (May 1995). Quadric and cubic bitetrahedral

patches. The Visual Computer, Volume 11, Number

5, pages 253–262.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3d surface construction algorithm.

Computer Graphics, Volume 21, Number 4, July 1987,

pages 163–169.

Luk, C. (2008). Tessellating algebraic curves and surfaces

using A-Patches. Master’s thesis, University of Wa-

terloo.

Ohtake, Y. and Belyaev, A. G. (December 2002). Dual-

primal mesh optimization for polygonized implicit

surfaces with sharp features. Journal of Computing

and Information Science in Engineering, Volume 2, Is-

sue 4, pages 277–284.

Peters, J. (1994). Evaluation and approximate evaluation of

multivariate bernstein form on a regularly partitioned

simplex. ACM Transactions on Mathematical Soft-

ware, 20(4):460–480.

Sederberg, T. W. (1985). Piecewise algebraic surface

patches. Computer Aided Geometric Design, Volume

2, Issues 1-3, pages 53–59.

Sederberg, T. W. and Anderson, D. (1985). Steiner surface

patches. Computer Graphics and Applications, IEEE,

Volume 5, Issue 5, pages 23–36.

Wang, J., Oliveira, M. M., and Kaufman, A. E. (2005).

Reconstructing manifold and non-manifold surfaces

from point clouds. 16th IEEE Visualization 2005 (VIS

2005), page 53.

Wyvill, B., Jepp, P., van Overveld, K., and Wyvill, G.

(2000). Subdivision surfaces for fast approximate im-

plicit polygonization.

TESSELLATING ALGEBRAIC CURVES AND SURFACES USING A-PATCHES