A KERNEL MAXIMUM UNCERTAINTY DISCRIMINANT

ANALYSIS AND ITS APPLICATION TO FACE RECOGNITION

Carlos Eduardo Thomaz

Department of Electrical Engineering, Centro Universitario da FEI, FEI, Sao Paulo, Brazil

Gilson Antonio Giraldi

Department of Computer Science, National Laboratory for Scientiﬁc Computing, LNCC, Rio de Janeiro, Brazil

Keywords:

Non-linear discriminant analysis, Limited sample size problems, Face recognition.

Abstract:

In this paper, we extend the Maximum uncertainty Linear Discriminant Analysis (MLDA), proposed recently

for limited sample size problems, to its kernel version. The new Kernel Maximum uncertainty Discriminant

Analysis (KMDA) is a two-stage method composed of Kernel Principal Component Analysis (KPCA) fol-

lowed by the standard MLDA. In order to evaluate its effectiveness, experiments on face recognition using the

well-known ORL and FERET face databases were carried out and compared with other existing kernel dis-

criminant methods, such as Generalized Discriminant Analysis (GDA) and Regularized Kernel Discriminant

Analysis (RKDA). The classiﬁcation results indicate that KMDA performs as well as GDA and RKDA, with

the advantage of being a straightforward stabilization approach for the within-class scatter matrix that uses

higher-order features for further classiﬁcation improvements.

1 INTRODUCTION

The primary purpose of Linear Discriminant Analy-

sis (LDA) is to separate samples of distinct groups

by maximizing their between-class separability while

minimizing their within-class variability (Fukunaga,

1990; Devijver and Kittler, 1982).

However, in limited sample and high dimensional

problems, such as face recognition, the within-class

scatter matrix is either singular or mathematically un-

stable and the standard LDA cannot be used to per-

form the separating task. In the last years, a number of

linear methods have been proposed to overcome this

difﬁculty (Swets and Weng, 1996; Belhumeur et al.,

1997; Chen et al., 2000; Yu and Yang, 2001; Yang

and Yang, 2003; Thomaz et al., 2006), making LDA

applicable to limited sample size problems that have

been assumed to be linearly separable in the original

space.

More recently, in order to make LDA applicable

to non-linearly separable data as well, kernel-based

methods have been applied. The main idea of kernel-

based methods is to map the original input data to a

feature space by a non-linear mapping where inner

products in the feature space can be computed by a

kernel function without knowing the non-linear map-

ping explicitly (Park and Park, 2005). Works in this

area include the Kernel Principal Component Anal-

ysis (KPCA) (Scholkopf et al., 1998), Generalized

Discriminant Analysis (GDA)(Baudat and Anouar,

2000), and Regularized Kernel Discriminant Analy-

sis (RKDA) (Lu et al., 2003), among others. In the

speciﬁc case of GDA, it has been demonstrated in

(Yang et al., 2004) that GDA is in fact equivalent to

the two-stage method composed of KPCA followed

by the standard LDA.

In this paper, we extend the Maximum uncer-

tainty Linear Discriminant Analysis (MLDA) ap-

proach (Thomaz et al., 2006), proposed recently for

solving limited sample size problems in discriminant

analysis, to its kernel or non-linear version. This non-

linear version of MLDA, here called Kernel Maxi-

mum uncertainty Discriminant Analysis (KMDA), is

a two-stage method composed of Kernel Principal

Component Analysis (KPCA) followed by the stan-

dard MLDA. The effectiveness of KMDA is evaluated

on face recognition through comparisons with KPCA,

GDA and RKDA, using the well-known Olivetti-

Oracle Research Lab (ORL) (Samaria and Harter,

1994) and FERET face databases (Phillips et al.,

341

Eduardo Thomaz C. and Antonio Giraldi G. (2009).

A KERNEL MAXIMUM UNCERTAINTY DISCRIMINANT ANALYSIS AND ITS APPLICATION TO FACE RECOGNITION.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 341-346

DOI: 10.5220/0001791003410346

 SciTePress

1998). One advantage of the proposed method for

face images is the possibility of improving classiﬁca-

tion performance by using more non-linear interme-

diate features than pixels in the images. In addition,

KMDA does not require the selection of parameters,

like RKDA, for within-class scatter matrix stabiliza-

tion.

The paper is organized as follows. In section 2

we review brieﬂy the LDA and MLDA approaches.

Then, in section 3, we explain how we have extended

the MLDA approach to its non-linear version using

the mathematical result described in (Yang et al.,

2004). The set up of the experiments carried out in

this work as well as the classiﬁcation results on face

recognition are presented respectively in sections 4

and 5, comparing the KMDA recognition rates with

KPCA, GDA and RKDA. In section 6, we analyze and

discuss the non-linear classiﬁcation results of KMDA

with the MLDA ones published in (Thomaz et al.,

2006). Finally, in section 7, we conclude the pa-

per, summarizing its main contribution and indicating

possible future work.

2 LINEAR DISCRIMINANT

ANALYSIS (LDA)

Let the scatter matrices between-class S

and within-

class S

be deﬁned, respectively, as

∑

i=1

− x)(x

− x)

(1)

and

∑

i=1

− 1)S

∑

i=1

∑

j=1

i, j

− x

)(x

i, j

− x

)

(2)

where x

i, j

is the n-dimensional pattern (or sample) j

from class i, N

is the number of training patterns from

class i, and g is the total number of classes or groups.

The vector x

and matrix S

are respectively the un-

biased mean and sample covariance matrix of class i

(Fukunaga, 1990). The grand mean vector x is given

x =

∑

i=1

∑

i=1

∑

j=1

i, j

, (3)

where N is the total number of samples, that is, N =

+ N

+ . . . + N

. It is important to note that the

within-class scatter matrix S

deﬁned in equation (2)

is essentially the standard pooled covariance matrix

multiplied by the scalar (N − g), where S

can be

written as

N − g

∑

i=1

− 1)S

+ (N

− 1)S

+ . . . + (N

− 1)S

N − g

(4)

The main objective of LDA is to ﬁnd a projection

matrix W

lda

that maximizes the ratio of the determi-

nant of the between-class scatter matrix to the deter-

minant of the within-class scatter matrix (Fisher’s cri-

terium), that is,

lda

= argmax



. (5)

The Fisher’s criterium described in equation (5)

is maximized when the projection matrix W

lda

composed of the eigenvectors of S

−1

with at most

(g − 1) nonzero corresponding eigenvalues (Fuku-

naga, 1990; Devijver and Kittler, 1982).

However, in limited sample and high dimensional

problems, such as face recognition, S

is either singu-

lar or mathematically unstable and the standard LDA

cannot be used to perform the separating task. To

avoid both critical issues, Thomaz et al. have cal-

culated W

lda

by using a maximum uncertainty LDA-

based approach (MLDA) that considers the issue of

stabilizing the S

estimate with a multiple of the iden-

tity matrix (Thomaz et al., 2004; Thomaz et al., 2006).

The MLDA algorithm can be described as fol-

lows:

1. Find the Ψ eigenvectors and Λ eigenvalues of S

where S

N−g

;

2. Calculate the S

average eigenvalue λ, that is,

λ =

∑

j=1

Tr(S

)

; (6)

3. Form a new matrix of eigenvalues based on the

following largest dispersion values

∗

diag[max(λ

, λ), max(λ

, λ), . . . , max(λ

, λ)];

(7)

4. Form the modiﬁed within-class scatter matrix

∗

= S

∗

(N − g) = (ΨΛ

∗

)(N − g). (8)

The MLDA method is constructed by replacing S

with S

∗

in the Fisher’s criterium formula described in

equation (5).

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

342

3 A KERNEL MLDA (KMDA)

Since the non-linear mapping of the original space to

a higher dimensional feature space would commonly

lead to an ill-posed within-class scatter matrix, the

aforementioned MLDA approach might be suitable

for solving not only the singularity and instability is-

sues of the linear Fisher methods, but also the Fisher

discriminant analysis with kernels.

Let a non-linear function φ that maps the input

sample space R

into the feature space F, as follows:

φ : x ∈ R

→ φ(x) ∈ F. (9)

The between-class and within-class scatter matri-

ces in the feature space F can be deﬁned, respectively,

∑

i=1

(φ

− φ)(φ

− φ)

(10)

and

∑

i=1

∑

j=1

(φ(x

i, j

) − φ

)(φ(x

i, j

) − φ

)

, (11)

where φ

is the mean of the training samples of class i

mapped into the feature space, that is,

∑

j=1

φ(x

i, j

), (12)

and φ is the grand mean vector of all the training sam-

ples mapped into the feature space, that is,

φ =

∑

i=1

∑

j=1

φ(x

i, j

). (13)

It is important to note that when φ(x) = x equations

(10) and (11) reduce to their corresponding linear ver-

sions described in equations (1) and (2), respectively.

Thus, according to the Fisher’s criterium de-

scribed in equation (5), the kernel LDA projection

matrix

lda

can be determined by calculating the

eigenvectors of

−1

with at most (g − 1) nonzero

corresponding eigenvalues. These eigenvectors are

then the optimal linear discriminant directions on the

feature space, which represent non-linear discrimi-

nant directions in the input sample space.

To extend the MLDA approach to its non-linear

(or kernel) version, we need essentially to replace

with

∗

, using the MLDA algorithm described in the

previous section. One way to do this would be to

perform the eigen-analyzes of

and

in the fea-

ture space, as proposed in (Lu et al., 2003). Alterna-

tively, we could use the more intuitive mathematical

result described in (Yang et al., 2004). According to

Yang et al. (Yang et al., 2004), the kernel LDA is in

fact equivalent to the two-stage method composed of

KPCA (Scholkopf et al., 1998) followed by the stan-

dard LDA.

Therefore, instead of solving the eigenvalue prob-

lem of

and

∗

directly in the feature space, we

perform ﬁrstly KPCA (Scholkopf et al., 1998) in the

input sample space, changing the dimension of fea-

ture space to m, and next the standard MLDA to ex-

tract the linear discriminant features in the non-linear

transformed space R

given by the KPCA projection.

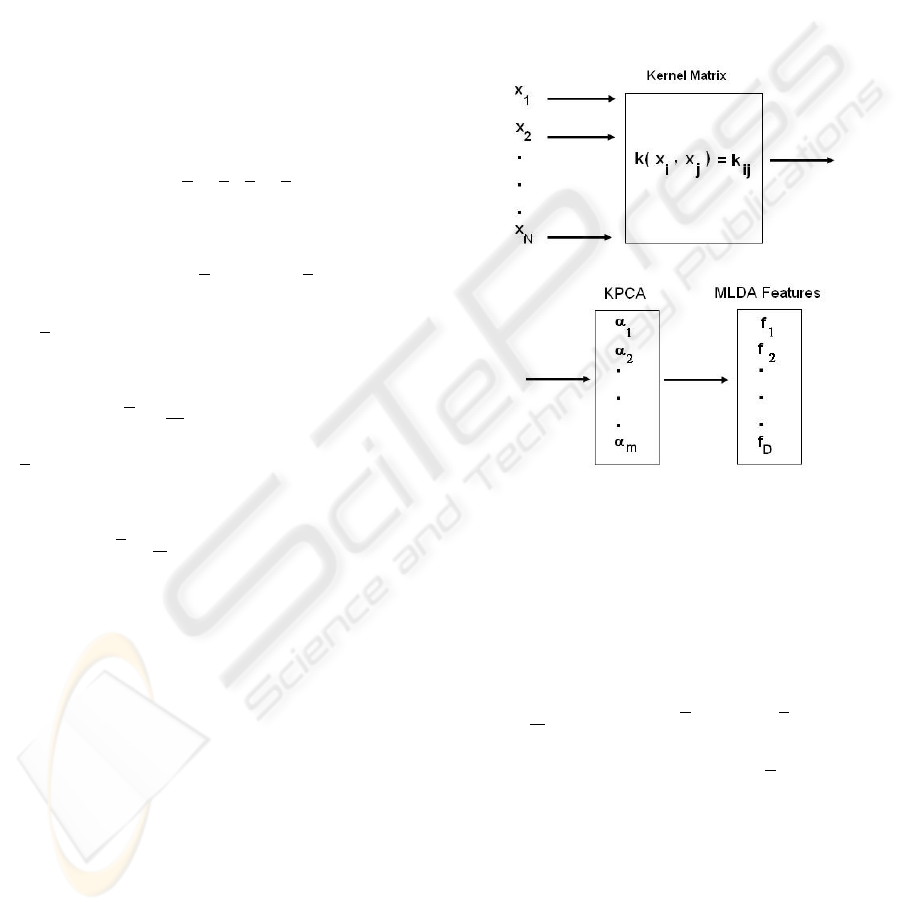
The whole process is summarized in Figure 1.

Figure 1: Pipeline of the KMDA method. Firstly, the ker-

nel matrix is generated from input samples and KPCA is

applied. Then, the standard MLDA is used to extract the D

discriminant features in the space given by KPCA projec-

tion, where D ≤ (g − 1).

The goal of KPCA is to diagonalize the covariance

matrix

S deﬁned as (Zheng et al., 2005):

S =

∑

i=1

∑

j=1

(φ(x

i, j

) − φ)(φ(x

i, j

) − φ)

. (14)

For simplicity, let us suppose that φ = 0. So, we

must ﬁnd the eigenvectors v and the corresponding

eigenvalues λ ≥ 0, solutions of the eigenequation:

λv =

Sv. (15)

However, in kernel methods we do not know the

function φ explicitly but a kernel k such that k (x, y) =

φ(x)

· φ(y). Thus, we must obtain a kernel version

of expression (15). In fact, it can be shown that the

eigenvectors v can be written as follows (Scholkopf

et al., 1998):

A KERNEL MAXIMUM UNCERTAINTY DISCRIMINANT ANALYSIS AND ITS APPLICATION TO FACE

RECOGNITION

343

v =

∑

i=1

∑

j=1

i j

φ(x

i, j

) = F (X)α, (16)

where F (X) =



φ(x

1,1

)φ(x

1,2

) · · · φ(x

g,N

)



, and

α =



· · · α



. By substi-

tuting (16) into (15), we obtain the KPCA eigenvalue

problem:

Nλα = Kα, (17)

where K =



ω,γ

= k (x

i, j

, x

s,t

)



, with ω = j + N

i−1

i−2

+ ... +N

and γ = t + N

s−1

+ N

s−2

+ ... +N

, is a

N × N matrix called kernel matrix.

The proposed strategy, that is KPCA+MLDA or

simply KMDA, is particularly useful when solving

limited sample and high-dimensional problems, be-

cause m is upper bounded by N, i.e. m ≤ (N − 1).

Since the MLDA approach deals with the singular-

ity and instability of the within-class scatter matrix in

such limited sample size situations, we have selected

m = (N − 1) to reproduce the total variability of the

samples in the feature space.

4 EXPERIMENTS

To evaluate the effectiveness of KMDA on face recog-

nition, comparisons with KPCA (Scholkopf et al.,

1998), GDA (Baudat and Anouar, 2000), and RKDA

(Lu et al., 2003), were performed using the well-

known Olivetti-Oracle Research Lab (ORL) (Samaria

and Harter, 1994) and FERET (Phillips et al., 1998)

face databases. Figure 2 shows some samples of these

datasets.

(a)

(b)

Figure 2: (a) A set of ten images of one subject from the

ORL face database. (b) Sets of four images of two subjects

from the FERET database.

We have implemented the KPCA, GDA and

RKDA using the respective authors’ Matlab codes

available at the following website: http://www.kernel-

machines.org/software.

For simplicity, an Euclidean distance classiﬁer

was used to perform classiﬁcation in the non-linear

feature space. Also, we have used only the well-

known Gaussian kernel

k(x

, x

) = exp(

−k x

− x

) (18)

to compute indirectly the non-linear transforma-

tions, where the δ parameter range was taken to be

[0.001, 0.002, 0.004, 0.008, 0.01, ..., 1.0] times the di-

mension of the input sample space n for all the afore-

mentioned algorithms tested.

To determine the regularization parameter η of

the RKDA approach (Lu et al., 2003), experimen-

tal analyzes were carried out based on the best clas-

siﬁcation accuracy given the following parameter

set [0.001, 0.01, 0.1, 0.2, ..., 0.9, 0.99, 0.999, 1.0]. The

best results were obtained when η = 0.001 for both

ORL and FERET experiments.

Each experiment was repeated 25 times using sev-

eral features. Distinct training and test sets were ran-

domly drawn, and the mean and standard deviation of

the recognition rate were calculated. The classiﬁca-

tion of the ORL 40 subjects was computed using for

each individual 5 images to train and 5 images to test.

In the FERET database with 200 subjects, the train-

ing and test sets were respectively composed of 3 and

1 frontal images.

Analogously to the experiments carried out in

(Thomaz et al., 2006), to represent a recognition prob-

lem where the within-class scatter matrix is singular,

the ORL face images were resized to 32x32 pixels,

that is, the total number of training observations was

N = 200 and the dimensionality of the original im-

ages was n = 1024. The FERET images were resized

to 16x16 pixels in order to pose an alternative pat-

tern recognition problem where the within-class scat-

ter matrix is non-singular but poorly estimated, i.e.,

N = 600 and n = 256.

5 RESULTS

Table 1 shows the maximum test average recognition

rates with standard deviation (std) of the ORL and

FERET datasets over the Gaussian kernel parameter

δ, and the corresponding number of principal (F1)

and discriminant (F2) features. The notation ’—’ in

the rows of Table 1 indicates that the corresponding

method has been calculated using either F1 or F2

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

344

features, but not both. In fact, KMDA is the only

discriminant kernel method investigated in this work

that is explicitly composed of a two-stage non-linear

transformation.

As we should expect, all non-linear discriminant

methods (GDA, RKDA and KMDA) led to higher

classiﬁcation results than KPCA.

Table 1: ORL and FERET classiﬁcation results.

Dataset Features

Method δ F1 F2 % (std)

ORL

KPCA 0.02*1024 160 — 93.0 (1.9)

GDA 0.08*1024 — 39 96.5 (1.3)

RKDA 1.00*1024 — 31 95.7 (1.3)

KMDA 1.00*1024 199 39 96.2 (1.6)

FERET

KPCA 0.10*256 599 — 92.3 (1.3)

GDA 1.00*256 — 104 95.0 (1.0)

RKDA 0.20*256 — 159 97.8 (0.8)

KMDA 1.00*256 599 20 98.3 (0.9)

In the ORL experiments, the best classiﬁcation

result was reached by GDA (96.5%), followed by

KMDA (96.2%) and RKDA (95.7%). Given the

similarity of these recognition rates and their corre-

sponding standard deviations, we cannot see clearly

an overall best classiﬁcation performance of any ker-

nel discriminant method in these experiments. Since

the ORL face database contains only 40 subjects to

be separated, the discriminant features of the kernel

Fisher-based methods were limited to 39 components.

Although in such experiments, where n(= 1024) >

N(= 200), the intermediate KPCA transformation

of KMDA allows the within-class and between-class

scatter matrices to be calculable in computers with a

standard memory size, KMDA requires a two-stage

ﬁnal transformation that uses more features than the

GDA and RKDA one-stage methods.

One advantage of using a non-linear two-stage

method such as KMDA in limited sample and high

dimensional problems can be seen in the FERET re-

sults. In this case, the discriminant features of the ker-

nel Fisher-based methods were limited to 199 compo-

nents, because the FERET dataset contains only 200

subjects to be separated. However, since N(= 600) >

n(= 256), the classiﬁcation performance of KMDA

can be further improved by using more non-linear in-

termediate features (N − 1 = 599) than there are pix-

els in the 16x16 images. In this application, where

the within-class scatter matrix was non-singular but

poorly estimated, KMDA achieved the best classiﬁ-

cation accuracy (98.3%) using a higher-order KPCA

transformation with 599 principal components fol-

lowed by an MLDA transformation composed of only

20 discriminant components.

Another KMDA advantage, comparing speciﬁ-

cally with the other regularized Fisher discriminant

method RKDA, is the fact that KMDA is based on a

straightforward stabilization approach for the within-

class scatter matrix, avoiding the RKDA optimization

for which the user has to select experimentally the

best η regularization parameter.

6 DISCUSSION

We have used the same ORL and FERET face

databases and carried out the same training and test

experiments described in (Thomaz et al., 2006) for

the standard MLDA. So, it is possible to compare

the classiﬁcation results of KMDA with the ones pre-

sented in (Thomaz et al., 2006) for MLDA.

Table 2 highlights the MLDA maximum test aver-

age recognition rates with standard deviation (std) of

the ORL and FERET datasets over the corresponding

number of principal (F1) and discriminant (F2) fea-

tures, as published in (Thomaz et al., 2006), and also

the KMDA results described previously in Table 1.

Table 2: MLDA versus KMDA classiﬁcation results.

Dataset Features

Method F1 F2 % (std)

ORL

MLDA — 39 95.8 (1.6)

KMDA 199 39 96.2 (1.6)

FERET

MLDA — 10 95.4 (1.4)

KMDA 599 20 98.3 (0.9)

As can be seen, for the ORL dataset with face im-

ages resized to 32x32 pixels, there is no signiﬁcant

classiﬁcation improvement in using KMDA rather

than MLDA in these experiments, because the corre-

sponding MLDA and KMDA recognition rates (and

standard deviations) are very similar. In such small

sample and high-dimensional problem, where the

two-stage KMDA could not extract higher-order fea-

tures because N(= 200) < n(= 1024), MLDA seems

the best choice because it is simpler and much faster

to compute.

However, the superiority of KMDA compared to

MLDA is clear in the FERET dataset with face im-

ages resized to 16x16 pixels. The KMDA classi-

ﬁer performed better than its linear version, achiev-

ing a higher maximum average classiﬁcation accuracy

with lower standard deviation. In these experiments,

KMDA outperformed MLDA by seeking discrimi-

nant hyperplanes not in the 256-dimensional origi-

A KERNEL MAXIMUM UNCERTAINTY DISCRIMINANT ANALYSIS AND ITS APPLICATION TO FACE

RECOGNITION

345

nal space, but in a much higher 599-dimensional fea-

ture space composed of non-linear transformations of

the original pixels. In such limited sample and high-

dimensional problem, where N(= 600) > n(= 256),

it seems that we can further improve the classiﬁcation

accuracy by exploring more features than is possible

in the linear case.

7 CONCLUSIONS

In this work, we extended the MLDA approach to its

non-linear version. This non-linear version of MLDA,

here called KMDA, is a KPCA+MLDA two-stage

method. To evaluate the KMDA effectiveness, ex-

periments on face recognition using the well-known

ORL and FERET face databases were carried out

and compared with other existing kernel discrimi-

nant methods, such as GDA and RKDA. The classi-

ﬁcation results indicate that KMDA performs as well

as GDA and RKDA, with the advantages of being a

straightforward stabilization approach for the within-

class scatter matrix that uses a pre-deﬁned number of

higher-order features whenever the number of train-

ing samples is larger than the original dimensionality

of the input data.

As future work, we intend to directly regularize

the eigen-analysis of the within-class scatter matrix in

the feature space, without a KPCA intermediate step.

ACKNOWLEDGEMENTS

The authors would like to thank the support provided

by PCI-LNCC, FAPESP (2005/02899-4), CNPq

(472386/2007-7) and CAPES (094/2007). Also, por-

tions of the research in this paper use the FERET

database of facial images collected under the FERET

program.

REFERENCES

Baudat, G. and Anouar, F. (2000). Generalized discriminant

analysis using a kernel approach. Neural Computa-

tion, 12(10):2385–2404.

Belhumeur, P. N., Hespanha, J. P., and Kriegman, D. J.

(1997). Eigenfaces vs. ﬁsherfaces: Recognition us-

ing class speciﬁc linear projection. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

19(7):711–720.

Chen, L., Liao, H., Ko, M., Lin, J., and Yu, G. (2000).

A new lda-based face recognition system which can

solve the small sample size problem. Pattern Recog-

nition, 33(10):1713–1726.

Devijver, P. and Kittler, J. (1982). Pattern Classiﬁcation: A

Statistical Approach. Prentice-Hall.

Fukunaga, K. (1990). Introduction to Statistical Pattern

Recognition. Morgan Kaufmann, San Francisco, 2nd

edition.

Lu, J., Plataniotis, K. N., and Venetsanopoulos, A. N.

(2003). Face recognition using kernel direct discrimi-

nant analysis algorithms. IEEE Transactions on Neu-

ral Networks, 14(1):117–126.

Park, C. H. and Park, H. (2005). Nonlinear discriminant

analysis using kernel functions and the generalized

singular value decomposition. SIAM J. Matrix Anal.

Appl., 27(1):87–102.

Phillips, P. J., Wechsler, H., Huang, J., and Rauss, P. (1998).

The feret database and evaluation procedure for face

recognition algorithms. Image and Vision Computing,

16:295–306.

Samaria, F. and Harter, A. (1994). Parameterisation of a

stochastic model for human face identiﬁcation. In

Proceedings of 2nd IEEE Workshop on Applications

of Computer Vision.

Scholkopf, B., Smola, A., and Muller, K.-R. (1998). Non-

linear component analysis as a kernel eigenvalue prob-

lem. Neural Computation, 10(5):1299–1319.

Swets, D. L. and Weng, J. J. (1996). Using discrimi-

nant eigenfeatures for image retrieval. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

18(8):831–836.

Thomaz, C. E., Gillies, D. F., and Feitosa, R. Q. (2004).

A new covariance estimate for bayesian classiﬁers in

biometric recognition. IEEE Transactions on Circuits

and Systems for Video Technology, Special Issue on

Image- and Video-Based Biometrics, 14(2):214–223.

Thomaz, C. E., Kitani, E. C., and Gillies, D. F. (2006). A

maximum uncertainty lda-based approach for limited

sample size problems - with application to face recog-

nition. Journal of the Brazilian Computer Society,

12(2):7–18.

Yang, J., Jin, Z., yu Yang, J., Zhang, D., and Frangi, A. F.

(2004). Essence of kernel ﬁsher discriminant: Kpca

plus lda. Pattern Recognition, 37:2097–2100.

Yang, J. and Yang, J. (2003). Why can lda be performed in

pca transformed space? Pattern Recognition, 36:563–

566.

Yu, H. and Yang, J. (2001). A direct lda algorithm for high

dimensional data - with application to face recogni-

tion. Pattern Recognition, 34:2067–2070.

Zheng, W., Zou, C., and Zhao, L. (2005). An improved al-

gorithm for kernel principal component analysis. Neu-

ral Process. Lett., 22(1):49–56.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

346