AN ANALYSIS OF SAMPLING FOR FILTER-BASED FEATURE

EXTRACTION AND ADABOOST LEARNING

Anselm Haselhoff and Anton Kummert

Communication Theory, University of Wuppertal, 42097 Wuppertal, Germany

Keywords:

Feature extraction, Sampling, AdaBoost.

Abstract:

In this work a sampling scheme for ﬁlter-based feature extraction in the ﬁeld of appearance-based object

detection is analyzed. Optimized sampling radically reduces the number of features during the AdaBoost

training process and better classiﬁcation performance is achieved. The signal energy is used to determine

an appropriate sampling resolution which then is used to determine the positions at which the features are

calculated. The advantage is that these positions are distributed according to the signal properties of the

training images.

The approach is veriﬁed using an AdaBoost algorithm with Haar-like features for vehicle detection. Tests

of classiﬁers, trained with different resolutions and a sampling scheme, are performed and the results are

presented.

1 INTRODUCTION

Video cameras facilitate application of various object

detection algorithms and especially appearance-based

methods gained interest since they are generally ap-

plicable to object detection problems. These methods

learn the characteristics of vehicle appearance from a

set of training images which capture the variability in

the vehicle class (Sun et al., 2004). Different combi-

nations of feature extraction methods and learning al-

gorithms are proposed (Sun et al., 2004), (Ponsa et al.,

2005) to form an appearance-based object detection

system.

The object detection system proposed by Viola &

Jones (Viola and Jones, 2001) is one of the most fre-

quently used systems (e.g. (Lienhart et al., 2002),

(Ponsa et al., 2005), (Overett and Petersson, 2007)).

The competitive edge is reached by means of the fast

computation of the Haar-like features and the cas-

caded structure of the classiﬁer. These facts make the

system work in real-time.

The system relies on a uniﬁed image resolution to

guarantee a comparable number of features to be ex-

tracted, where uniﬁed means that all images used for

training have the same resolution. This choice of res-

olution is highly related to sampling. Obviously using

a too low resolution leads to a lack of important infor-

mation and in turn unsatisfying classiﬁcation results

are obtained. In contrast, using a very high resolu-

tion the learning algorithm has to cope with the risk

of concentrating on too speciﬁc object properties and

the computational load grows rapidly.

The scale selection of the features, which is

’equivalent’ to image scale selection, is implicitly

done by the feature selector that chooses the size of

the Haar-like features. Thus, the task is rather to offer

the feature selector included in the learning algorithm

a wide range of possible feature scales which capture

the most information of the training data while pre-

serving low computational complexity.

The image resolution can be explicitly changed by

resizing the images or implicitly changed by scaling

the features and calculate them at certain sampling

positions. Concerning the latter case, the obvious so-

lution is to use equally-spaced sampling positions in

horizontal and vertical direction. This is just a speciﬁc

case of multidimensional sampling where no mutual

dependency between different dimensions is consid-

ered. The dependencies between different dimensions

can be used to improve the efﬁciency of the sampling

in terms of the number of sampling points.

In this work a sampling methodology is presented

that can be adjusted to the training data at hand and

different sampling options are exposed. On the one

hand the number of sampling points can be reduced

while preserving the same signal energy and on the

180

Haselhoff A. and Kummert A. (2009).

AN ANALYSIS OF SAMPLING FOR FILTER-BASED FEATURE EXTRACTION AND ADABOOST LEARNING.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 180-185

DOI: 10.5220/0001791201800185

 SciTePress

other hand the number of sampling points can be

ﬁxed, but by means of a different sampling scheme

more energy is preserved.

The remainder of the paper proceeds as follows.

Firstly, section 2 gives a brief description of the used

learning algorithm and features. Secondly, in section

3 the key ideas of 2D sampling are summarized. Next,

in section 4 the sampling methodology is presented

and ﬁnally, the results of trained classiﬁers with dif-

ferent training resolutions and the sampling scheme

are presented. The classiﬁcation accuracy conﬁrms

the advantages of the presented sampling scheme.

2 DETECTION ALGORITHM

2.1 Haar-like Features

In the object detection system developed by Viola &

Jones (Viola and Jones, 2001) Haar-like features are

proposed, called rectangle features. The advantage of

these features is a very fast computation due to the use

of the integral image.

For the training process, an exhaustive set of fea-

tures is used from which the AdaBoost algorithm can

select the most important ones. The feature values are

obtained by applying the ﬁlters in different scales to

varying positions on an image. The ﬁve basic types of

rectangular ﬁlter masks (band-pass ﬁlters) are shown

in ﬁgure 1.

1-1

-1

-2

1 1

-1

-2

Figure 1: Five basic types of rectangular ﬁlter masks.

2.2 The Boosting Algorithm

The feature representation is used for the training of

the classiﬁer by means of an AdaBoost algorithm.

AdaBoost performs a feature selection and combines

the selected features as simple weak classiﬁers to a

strong one. In each iteration step of the AdaBoost al-

gorithm the weak classiﬁer with the smallest weighted

classiﬁcation error is selected. Each weak classiﬁer is

dependent on just one component of the feature vector

and the classiﬁcation is done via a simple threshold

comparison.

A strong classiﬁer is trained with the discrete Ad-

aBoost (Viola and Jones, 2001) algorithm and is de-

ﬁned as

H(x) =



∑

t=1

(x) ≥

∑

t=1

0, otherwise

x x

xxx

x x x

Figure 2: Rectangular sampling in the frequency domain.

Grayish area denotes the rectangular base band and dashed

lines denote the spectral copies. ω

and ω

are the cut-off

frequencies in x- and y- direction respectively. The sam-

pling frequency matrix Ω

Ω

rect

is constructed using the vec-

tors Ω

Ω

and Ω

Ω

where x is the feature vector of an image, h

∈ {0,1}

is a weak classiﬁer, α

is the weight of the t-th weak

classiﬁer and T is the number of features selected.

The weak classiﬁers are combined by a weighted ma-

jority vote to a strong classiﬁer H.

After the ofﬂine learning process only a few se-

lected features must be calculated for online classiﬁ-

cation.

3 SAMPLING OF 2D SIGNALS

3.1 Naming Conventions and Basics

In the following sections f(x,y) = f (r) denotes a 2D

singal or image with r = (x, y)

, where a superscript

T denotes transposition. The same shorthand notation

is used for the Fourier transform.

For a 2D continuous function f(r) the Fourier

transform F( jω

ω)

s c

f(r) with ω

ω = (ω

,ω

)

is de-

ﬁned as

f(r) =

(2π)

F( jω

ω)e

jω

dω

ω (1)

F( jω

ω) =

f(r)e

− jω

dr. (2)

3.2 2D Sampling

The transition from 1D to 2D signals, like images,

comes along with new concepts related to sampling.

AN ANALYSIS OF SAMPLING FOR FILTER-BASED FEATURE EXTRACTION AND ADABOOST LEARNING

181

These concepts are caused by the mutual dependen-

cies across different dimensions. In 2D the sampling

period becomes a sampling matrix

T =





= (T

The sampled signal f

(r) and the continuous signal

f (r) are then connected by

(r) =

∑

n∈Z

f (Tn)δ(r− Tn). (3)

In analogy with the 1D case, the relation of the sam-

pling matrix T and the sampling frequency Ω

Ω

Ω is given

Ω

Ω = 2π





−1

, (4)

where Ω

Ω

Ω is a matrix as well with

Ω

Ω =



Ω



= (Ω

Ω

,Ω

Ω

This sampling frequency matrix Ω

Ω

Ω deﬁnes where the

spectral copies of the base band are located. Depend-

ing on the spectral properties of the signal at hand an

appropriate sampling scheme can be chosen. In Ohm

(Ohm, 2004) the following sampling schemata are

discussed: rectangular, shear, hexagonal, and quin-

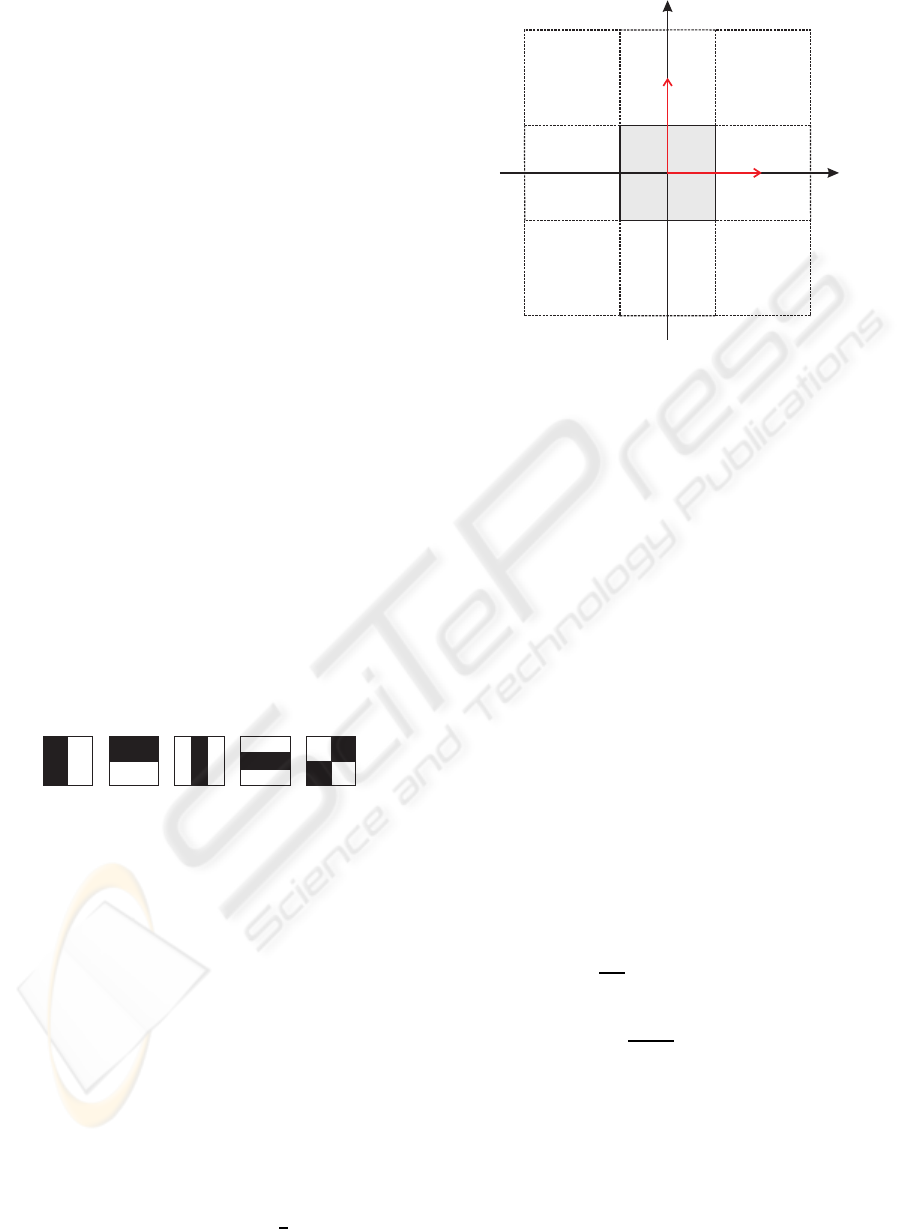
cunx sampling. The simplest option is the rectangu-

lar sampling with a ﬁxed step-width T for both direc-

tions, so that

T = T



1 0

0 1



. (5)

The sampling can be adjusted to the signal properties

for each direction. For example if an image signal has

high frequency components in the x-dimension and a

very ﬁne-grained sampling has to be chosen, this is

not necessarily required for the y-dimension. This is

an important aspect since images are generally resized

preserving the same width to height ratio.

The impact of rectangular sampling with the base

band and its periodic replications are visualized in

ﬁgure 2. The width to height ratio is not ﬁxed and

and ω

are the cut-off frequencies in x- and y-

dimension respectively. The resulting sampling fre-

quency is then

Ω

rect



2ω

0 2ω



= (Ω

Ω

,Ω

Ω

Using equation 4 the appropriate sampling matrix can

be obtained

rect



π/ω

0 π/ω



The difference between 1D and 2D sampling is

that the sampling positions of one dimension can

xxx

x x x

x x

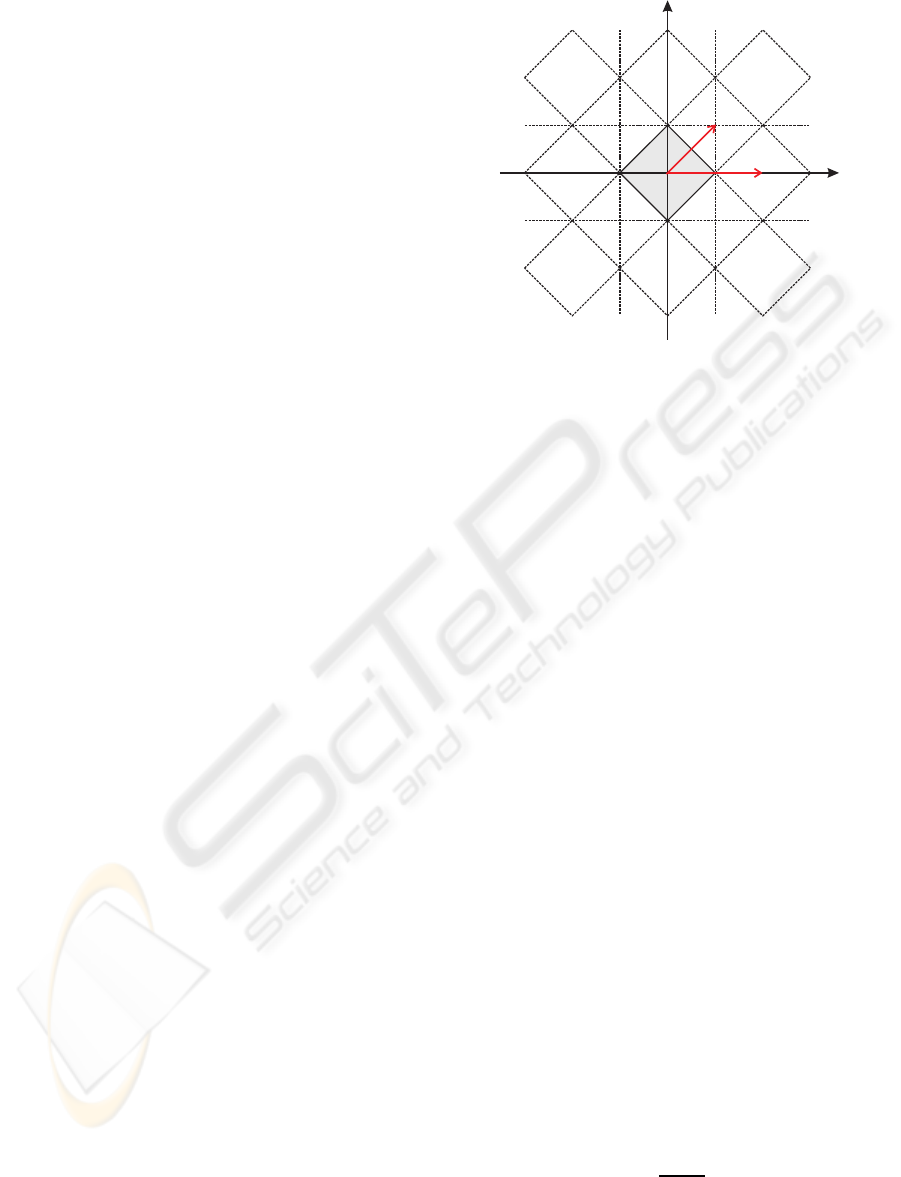
Figure 3: Quincunx sampling in the frequency domain.

Grayish area denotes the rhombus-like base band and

dashed lines denote the spectral copies. ω

and ω

are

the cut-off frequencies in x- and y- direction respectively.

The sampling frequency matrix Ω

Ω

quin

is constructed using

the vectors Ω

Ω

and Ω

Ω

be chosen depending on those of another dimension

(non separable sampling). For example the quincunx

sampling (Ohm, 2004) is a none separable sampling,

where the shape of the base band is rhombus like. Fig-

ure 3 shows a rhombus shaped base band and the ac-

cording periodic replications. It is obvious that one

possible solution to get the sampling frequencymatrix

is to choose Ω

Ω

= (2ω

,0)

and Ω

Ω

= (ω

,ω

)

As a result the sampling frequency is

Ω

quin



2ω

0 ω



and the corresponding sampling matrix is given by

quin



π/ω

−π/ω

2π/ω



3.3 Signal Energy in 2D

Generally, it can be assumed that using sampling

means losing information. To get an idea of how cru-

cial this error is, the energy can be regarded. The en-

ergy of a signal f(r) is deﬁned as

E =

| f(r)|

dr. (6)

Parseval’s theorem (Ohm, 2004) can be used to mea-

sure the energy in the frequency domain

| f(r)|

dr =

(2π)

|F( jω

ω)|

dω

ω. (7)

With these equations a measure to assess the signal

energy that is preserved in a sampled signal can be

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

182

deﬁned. The energy of the sampled signal can be ap-

proximated by

(2π)

|F( jω

ω)|

dω

ω. (8)

D denotes a set which is determined by the cut-off fre-

quencies and the sampling method. For a rectangular

sampling the set can be deﬁned as follows

rect





∈ R

||ω

| ≤ ω

∧ |ω

| ≤ ω



Analogously a set for the quincunx sampling can be

derived as

quin





∈ R

|ω

≤ 1



Finally, the energy packing efﬁciency η

of a

sampled signal can be deﬁned as the relative portion

of the energy that is preserved in the sampled signal.

This ratio of energy E

and the energy E

ref

of a refer-

ence signal (e.g. the energy E of the continuous sig-

nal) is a measure to compare different sampling rates.

ref

(9)

4 2D SAMPLING FOR IMAGE

FEATURE EXTRACTION

In general, the camera parameters and the distance

in which each training image was collected would be

needed to determine the sampling matrix and thus en-

able the usage of the equations from section 3. For our

experiments it is assumed that this information is not

available. Therefore no information about the sam-

pling period in world coordinates is given and some

assumptions have to be made. It is assumed that the

resolution M × N is the highest possible resolution.

Generally speaking, this is the highest image resolu-

tion that can be found in the trainingset. This image

resolution is used as the reference resolution which is

our optimal case and takes the place of our continuous

signal.

The proposed sampling approach is divided into

two parts. The goal of the ﬁrst part is to get those pa-

rameters that are necessary to calculate the sampling

matrix in the second part. These are either the number

of sampling points or the energy packing efﬁciency.

Firstly, a reasonable training resolution M

′

× N

′

has

to be deﬁned. Therefore the approach presented in []

can be used or a ﬁxed resolution can be set in advance

(e.g. 32× 24 for vehicle detection). At this point the

energy packing efﬁciency for this speciﬁc resolution

has to be calculated in reference to M × N using the

equations from section 3. To reach this goal all train-

ing images are resized to the maximal resolution of

M × N and afterwards the mean value of the discrete

Fourier transform (DFT) is calculated. The DFT is

then used in combination with equation 8 and D

rect

determine the energy packing efﬁciency for the reso-

lution M

′

× N

′

. In this context, the cut-off frequencies

are directly connected to the resolution using rectan-

gular sampling. For the maximal resolution the cut-

off frequencies are ﬁxed, so that ω

= π and ω

= π.

The cut-off frequencies ω

′

and ω

′

for a downsam-

pled image are then connected to M

′

× N

′

(10)

and

′

. (11)

Thus, the sampling frequency Ω

Ω

rect

and the energy

packing efﬁciency η

can be obtained for all resolu-

tions up to M × N.

In the second part an optimized sampling matrix

has to be determined e.g. for quincunx sampling

quin

. To ﬁnd this sampling matrix one of two op-

timization constraints can be chosen. The ﬁrst one is

to use the energy packing efﬁciency, so that the new

sampling matrix leads to the same value of η

that

was deﬁned in the ﬁrst part, but using fewer sampling

positions. These positions are distributedaccording to

the signal properties of the images. The second option

is to use the same number of sampling points and ﬁnd

an arrangement of sampling points that preserve more

energy. In this paper the ﬁrst option is discussed.

The procedure is almost the same as in part one.

The difference lies in the aspect how the sampling ma-

trix is determined. Now, equation 8 and D

quin

is used

for all different combinations of ω

′

and ω

′

. Thus

for all combinations the energy packing efﬁciency

can be calculated. Afterwards these values for ω

′

and ω

′

are chosen whoes corresponding energy efﬁ-

ciency value is closest to the predeﬁned value η

and

which would result in the lowest number of sampling

points. These sampling periods can then be used to

generate a sampling grid which serves as a rule where

the Haar-like features should be calculated.

5 RESULTS AND CONCLUSIONS

In this section the results provided by the proposed

approach described in the previous sections are dis-

cussed and the performance results of the trained clas-

siﬁers are presented. As already mentioned the object

AN ANALYSIS OF SAMPLING FOR FILTER-BASED FEATURE EXTRACTION AND ADABOOST LEARNING

183

detection system developed by Viola & Jones (Viola

and Jones, 2001) is used to verify the approach. The

trainingset consists of 2600 vehicle rear view images

as positive samples and 7007 other images as negative

samples, whereas the independent testset comprises

1114 vehicle rear views and 3003 negative samples.

These manually labeled images are collected from the

Label-Me (Russell et al., 2005) database. To enable

the Haar-like features to capture the edges of the ve-

hicles ten percent of the background is added at the

edges of the images.

For this training- and testset the maximal reso-

lution M × N is 256 × 192, with the same width to

height ratio as presented in (Ponsa et al., 2005). Now

the energy packing efﬁciency for different resolutions

′

× N

′

up to 256 × 192 can be calculated. Fig. 4

shows the energy packing efﬁciency for progressively

increasing resolution. For a width smaller than 20

pixels the energy is rapidly decreasing, hence choos-

ing a resolution higher than 20× 15 is reasonable. In

this work a training resolution of 32× 24 is chosen,

which is intentionally large compared to other exper-

imental results (e.g. (Ponsa et al., 2005), (Lienhart

et al., 2002)).

0 20 32 100 150 200 250

0.82

0.84

0.86

0.88

0.9

0.92

0.94

0.96

0.98

0.988

image width

energy packing efficiency

Figure 4: Energy packing efﬁciency for progressively in-

creasing resolution.

For this resolution η

= 0.988 is obtained, which

means that 98.8% of the energy of the reference im-

age with maximal resolution is preserved. The sam-

pling matrix with reference to 256 × 192 is

rect



8 0

0 8



By inspecting the DFT of the training images it be-

comes obvious that the high frequency components

are rather located in the vertical direction (see ﬁg. 5).

This means that our vehicle training images contain

many strong horizontal edges. This fact should be

considered choosing a sampling scheme. It would be

more effective to choose a high resolution in the ver-

tical and a smaller resolution in the horizontal dimen-

sion. This is essentially the outcome of the optimiza-

50 100 150 200 250

100

120

140

160

180

areas containing

98.8% of the energy

Figure 5: Rectangular and Quincunx base band for the train-

ing data preserving 98.8% of the energy. Rectangular and

Quincunx sampling are denoted by the solid and dashed

lines, respectively.

tion procedure from the last section with the quincunx

sampling, where the algorithm is constrained to ﬁnd a

sampling matrix T which results in preserving 98.8%

of the energy. Regarding the reference resolution, the

optimal sampling scheme is given by

quin



12.8 0

−6.4 12.8



The corresponding base bands for rectangular and

quincunx sampling are shown in ﬁgure 5. The quin-

cunx sampling is marked by the dashed line and the

rectangular sampling is marked by the solid line.

Since both methods cover the same energy of the im-

age signals the interesting part is the reduction in sam-

pling points. For the resolution of 32 × 24 the num-

ber of sampling points is 768 and for the quincunx

sampling the number is reduced by more than 50% to

just 300 sampling points. The sampling grids for both

methods are visualized in ﬁgure 6. The advantage of

the quincunx sampling is that mutual dependencies

across the x- and y-dimension are considered and that

a higher resolution in vertical than in horizontal di-

mension is achieved.

(a) Rectangular sampling (b) Quincunx sampling

Figure 6: Rectangular (768 sampling points) and Quincunx

(300 sampling points) sampling grid.

For the evaluation, three classiﬁers are trained us-

ing an AdaBoost algorithm with the same training pa-

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

184

rameters. All classiﬁers have 100 features and the dif-

ference between these classiﬁers is the training image

resolution. Two classiﬁers are trained by resizing the

images to a resolution of 16×12 and 32×24, respec-

tively. For these classiﬁers the sampling matrix is

rect



1 0

0 1



This sampling matrix is common practice and means

that the ﬁve Haar-like features (Fig. 1) are calculated

at all image coordinates.

The third classiﬁer uses the quincunx sampling

method. To perform this sampling, a minimal reso-

lution of 40 × 30 is required. After resizing the im-

age just these positions are used for feature calcula-

tion which are determined by the quincunx sampling

matrix

quin



2 0

−1 2



It is to mention that the minimal size of the Haar-like

features is set to be 2 × 2. Table 1 shows the number

of sampling points and features that are extracted dur-

ing the training process. The performance results of

Table 1: Trained classiﬁers.

Resolution Sampling Points Features

16× 12, T

rect

192 15· 10

32× 24, T

rect

768 260· 10

40× 30, T

quin

300 160· 10

the different classiﬁers are illustrated by using ROC

curves as shown in Fig. 7. The results reveal that the

best classiﬁcation performance is obtained by using

the resolution 40 × 30 with the sampling method and

unsatisfying performance by the resolution 16 × 12.

Even though the best classiﬁer’s feature pool is signif-

icantly smaller than the number of features used for

the classiﬁer with resolution 32 × 24 the results are

slightly better. This strengthens the assumption that

the proposed sampling method is valid and moreover

can even improve classiﬁcation performance without

increasing the computational load during the training

process.

Summing up, an approach has been introduced

to generate a sampling grid to determine reasonable

positions for calculating the Haar-like features. On

the one hand the number of features is reduced by

around 40% and the classiﬁcation accuracy is in-

creased. These advantages are due to the better uti-

lization of positions for feature calculation which are

adapted to the properties of the training images. One

aspect that should be included in future work is to

transfer this methodology directly to the Haar-like

−3

−2

−1

0.8

0.85

0.9

0.95

false positive rate

true positive rate

16x12

32x24

40x30, T

quin

Figure 7: ROC curve of three equally trained classiﬁers us-

ing two different cartesian and the quincunx sampling.

features to further reduce the computational complex-

ity without losings in accuracy.

REFERENCES

Lienhart, R., Kuranov, A., and Pisarevsky, V. (2002). Em-

pirical analysis of detection cascades of boosted clas-

siﬁers for rapid object detection. Technical report,

Mic. Research Lab, Intel Corporation, Santa Clara,

CA 95052, USA.

Ohm, J.-R. (2004). Multimedia Communication Technol-

ogy. Springer, Berlin, Heidelberg, Germany.

Overett, G. and Petersson, L. (2007). Boosting with multi-

ple classiﬁer families. Proc. of IEEE Intelligent Vehi-

cles Symposium, pages 1039–1044.

Ponsa, D., Lopez, A., Lumbreras, F., Serrat, J., and Graf,

T. (2005). 3d vehicle sensor based on monocular vi-

sion. In Proc. of the 8th Int. IEEE Conf. on Intelligent

Transportation Systems, Vienna, Austria.

Russell, B., Torralba, A., and Freeman, W. T. (2005). La-

belme image database. http://labelme.csail.mit.edu.

Sun, Z., Bebis, G., and Miller, R. (2004). On-road vehicle

detection using optical sensors: A review.

Viola, P. and Jones, M. (2001). Rapid object detection us-

ing a boosted cascade of simple features. In Accepted

Conf. on Computer Vision and Pattern Recognition.

AN ANALYSIS OF SAMPLING FOR FILTER-BASED FEATURE EXTRACTION AND ADABOOST LEARNING

185