
IMAGE RECTIFICATION
Evaluation of Various Projections for Omnidirectional Vision Sensors using the
Pixel Density
Christian Scharfenberger, Georg Faerber and Florian Boehm
Institute for Realtime-Computersystems, Technische Universitaet Muenchen, Arcisstrasse 21, 80333 Munich, Germany
Keywords:
Omnidirectional vision, Image rectification, Image quality, Calibration, Pixel density.
Abstract:
Omnidirectional vision sensors provide a large field of view for numerous technical applications. But the
original images of these sensors are distorted, not simply interpretable and not easy to apply for normal image
processing routines. So image transformation of original into panoramic images is necessary using various
projections like cylindrical, spherical and conical projection, but which projection is best for a specific appli-
cation?
In this paper, we present a novel method to evaluate different projections regarding their applicability in a
specific application using a novel variable, the pixel density. The pixel density allows to determine the resolu-
tion of a panoramic image depending on the chosen projection. To achieve the pixel density, first the camera
model is determined based on the gathered calibration data. Secondly, a projection matrix is calculated to map
each pixel of the original image into the chosen projection area for image transformation. The pixel density is
calculated based on this projection matrix in a final step.
Theory is verified and discussed in experiments with simulated and real image data. We also demonstrate that
the common cylindrical projection is not always the best projection to rectify images from omnidirectional
vision sensors.
1 INTRODUCTION
Many technical tasks require perspective cameras to
provide useful information of the surrounding envi-
ronment. Examples of common application fields
are obstacle detection, people tracking and detec-
tion. Therefore, cameras are used for driver assis-
tance systems in cars and robotics. There are a cou-
ple of reasons to use perspective cameras for differ-
ent tasks. However, it is desirable in some applica-
tions of computational vision to use vision sensors
with a large field of view. Teleconferencing, remote
surveillance and texture for model acquisition for vir-
tual reality benefit from camera systems providing
a large field of view. But normal perspective cam-
era systems are limited in their fields of view. To
overcome this limitation, researchers and practition-
ers developed camera systems containing either ro-
tating (Krishnan and Ahuja, 1996) or multiple cam-
eras (Utsumi et al., 1998). Other, quite effective ways
to enhance the field of view are camera systems us-
ing wide angle lenses like fisheye lenses or mirrors
in conjunction with lenses (Ishiguro, 1998; Daniilidis
and Geyer, 2000; Baker and Nayar, 1999). Omnidi-
rectional vision systems are catadioptric systems and
combine a curved mirror with a perspective camera to
obtain a large field of view. In the past, several con-
cepts for optical characteristics such as single view-
point (Baker and Nayar, 1999), (Yamazawa et al.,
1993), equi-resolution (Gaspar et al., 2002) and equi-
areal (Hicks and Perline, 2002) have been developed
to improve omnidirectional camera systems.
1.1 Related Work
Original images of omnidirectional camera systems
are distorted, not simply interpretable and not easy ap-
plicable to normal image processing routines. Meth-
ods and procedures exist which process original im-
ages even of uncalibrated omnidirectional vision sen-
sors, but no useful correlation between real object
properties like size and width can be found in origi-
nal images. So there is a need for conventional image
processing routines requiring transformed panoramic
images as well as calibration information. Yamazawa
et al. (Yamazawa et al., 1993) propose methods to
82
Scharfenberger C., Faerber G. and Boehm F. (2009).
IMAGE RECTIFICATION - Evaluation of Various Projections for Omnidirectional Vision Sensors using the Pixel Density.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 82-89
DOI: 10.5220/0001791700820089
Copyright
c
SciTePress

transform warped images into cylindric panoramic
images using cylindric coordinates. In (Yamazawa
et al., 1998), images of omnidirectional vision sen-
sors (ODVS) are transformed into images as if taken
directly with an ordinary camera. These images are
suitable for further data analysis, so that conventional
image processing routines can be utilised. Gandhi and
Trivedi (Gandhi and Trivedi, 2004) use ODVS’s with
single viewpoints. Knowing the exact parameters of
the hyperbolic mirror and the camera, they present a
plane transformation method to transform an image
to a perspective view looking downwards. Geyer and
Daniilidis propose in (Geyer and Daniilidis, 2001) a
unifiying model for the projective geometry and stu-
died its properties as well as its practical application.
1.2 Motivation
As shown above, various projections are developed
to transform original images into unwarped, rectified
images for a better use of conventionalimage process-
ing routines. However, there has been no evaluation in
literature that studies and evaluates different projec-
tions types to obtain best utilisation of sensor pixels
in rectified images. In this paper, we propose a novel
value, the pixel density, which characterises the con-
sistence of rectified image pixels with sensor pixels
at a certain position. Using the characteristics of the
pixel density, the projection for a specific camera sys-
tem can be chosen for best utilisation of sensor pixels
in rectified images. But the pixel density does not
predict the distortion of rectified images for a chosen
projection. We assume, that the pixel density depends
on the chosen projection, the distance between mirror
and camera, the field of view of the camera and on the
chosen mirror surface. So we conduct experiments on
synthesised and real images of ODVS’s with different
hyperbolic mirrors, different field of views, different
distances between mirror and camera as well as var-
ious projections. This paper is organised as follows:
The camera model and the calibration of omnidirec-
tional vision sensors is introduced in section 2.1 and
in section 2.2. We present the rectification methods
and the pixel density in section 3 and illustrate our re-
sults in section 4. The paper ends with a discussion
and conclusion in section 4.2 and section 5.
2 CAMERA CALIBRATION
2.1 Camera Model
We designed ODVS’s based on the well illustrated
SPOV theorem of Nayar and Baker (Baker and Na-
yar, 1999).
z−
c
2
2
− r
2
k
2
− 1
=
c
4
4
k− 2
k
(1)
z−
c
2
2
+ r
2
k
2
+ 1
=
2k+ c
2
4
(2)
Equation (1) for k ≤ 2 and equation (2) for k ≥
2 dimension ODVS’s with single points of view
(SPOV), whereas k specifies the mirror surface and
c the distance between SPOV and pinhole of the per-
spective camera. Furthermore, equation (3) fulfils the
SPOV theorem for many mirror types like hyperbolic
mirrors.
1
a
h
2
z−
c
2
2
−
1
b
h
2
= 1 with
a
h
=
c
2
r
k− 2
k
and b
h
=
c
2
r
2
k
(3)
In this paper, we use equation (3) to design some
real and synthesised mirrors, but we use distances dif-
ferent than c for technical reasons as well as to iden-
tify the properties of the pixel density. Using hyper-
bolic mirros, the SPOV constraint is only valid for
an accurate alignment of mirror and camera. But it is
difficult to achievean exact alignment between mirror
and camera, so that the camera system must be cali-
brated to compensate misalignments and to get a pre-
cise relation between world and camera coordinates.
2.2 Calibration
To determine the position of object points, the func-
tion f(~p) (4) which describes a relation between ~p in
world coordinates x
P
, y
P
and z
p
and the camera coor-
dinates u
P
and v
P
has to be found (see Figure 1(a)).
~
P =
u
P
v
P
= f(~p) with ~p = λ ·
x
p
y
p
z
p
, λ > 0 (4)
There exists many methods (Mei and Rives, 2007;
Colombo et al., 2007; Baker, S. and Nayar, S., 2001;
Micusik and Pajdla, 2004; Scaramuzza et al., 2006a)
proposing calibration to determine the function f(~p).
We use the calibration method developed by Scara-
muzza et al. (Scaramuzza et al., 2006b). All points
on a vector ~p in world coordinates (Figure 1(a)) are
mapped to the corresponding point P
′′
on the virtual
plane E
′′
(Figure 1(b)). Scaramuzza et al. propose the
IMAGE RECTIFICATION - Evaluation of Various Projections for Omnidirectional Vision Sensors using the Pixel Density
83

x
y
z
0
P
u’’
v’’
0
P’’
(a) World to virtual
sensor plane E
′′
0
u’’
v’’
P’’
(b) Point P
′′
on the virtual
sensor plane
0
u
v
P
(c) Real sensor plane
Figure 1: The camera model (a) used in this paper. The
world point P is mapped on a virtual sensor plane E
′′
(b)
and the projection transformed to the real sensor plane (c)
using affine transformations.
relation between world and virtual sensor plane as
~p =
x
p
y
p
z
p
= λ·
u
P
′′
v
P
′′
f(ρ)
=
x
p
y
p
a
0
+ a
2
ρ
2
+ ... + a
N
ρ
N
(5)
with λ = 1 and ρ =
q
x
2
~p
+ y
2
~p
. Furthermore, they ap-
proximate the component z of f(~p) depending on the
curvature as a n-polynomial function. The relation
between the real sensor plane and the virtual sensor
plane is realised as an affine transformation (see equa-
tion 6).
~
P
′′
= A·
~
P+
~
t with A =
c d
d 1
~
P =
u
P
v
P
and
~
t =
u
center
v
center
(6)
The parameters a
0
... a
n
, A and
~
t are the calibration
parameters.
3 IMAGE RECTIFICATION
First the projection area in world coordinates based on
individual projection parameters like width M, height
),,( ZYXf
v
u
=
ú
û
ù
ê
ë
é
Interpolation
UndistortedImage
Projection-
parameters
CalibrationData
Source
Cameramodel
0
u
v
0
n
m
Worldcoordinates
ofprojectionsurface
X, Y,Z
Calculationof
projectionsurface
Figure 2: This figure illustrates the rectification of non
panoramic images. We calculate the projection area and
transform original images to unwarped image using the
gathered calibration data. A bicubic interpolation method
is used for interpolation.
X
Y
α
offset
α
α/2
d
P
α
P
(a) Top view
Z
Y
P
Z
top
Z
bottom
Z
P
(b) Side view
Figure 3: This figure shows the cylindrical projection pa-
rameters in top and side view.
N and region of interest (ROI) is determined. Each
pixel [m,n]
T
of the projection area is stored in a M x
N x 3 dimensional matrix F containing its world co-
ordinates X(m,n), Y(m,n) and Z(m,n). Furthermore,
the sensor coordinates of the projection area are then
calculated using the camera model as well as the cal-
ibration data and stored in a matrix (LUT). Based on
the calibrated camera model, images are rectified us-
ing the LUT and a bicubic interpolation method. Fig-
ure 2 illustrates this workflow. We also postulate the
view of the perspective camera in z - direction for all
projections.
3.1 Cylindrical Projection
A common projection is the cylindrical projection.
Parameters for the cylindrical projections are distance
to the projection area d, rotation width α, rotation off-
set α
of f set
, and the height of the cylinder given by Z
top
and Z
bottom
(see Figure 3(a) and 3(b)). Based on these
parameters, first the cylindrical coordinates (α
P
,Z
P
)
T
at position [m, n]
T
in the target image with width M
and height N are calculated (see equation (7)).
~
P
F m,n
=
d
α
P
Z
P
=
d
α
of f set
−
α
2
+
α
M
· m
Z
top
−
Z
top
−Z
bottom
N
· n
(7)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
84
X
Y
α
offset
α
α/2
P
α
P
d
bottom
d
P
d
top
(a) Top View
Y
Z
P
Z
top
Z
bottom
Z
P
(b) Side View
Figure 4: The parameters of conic projection are shown in
this figure and define the projecton area.
3.2 Conic Projection
The projection area of the conic projection relates to
a cone cut-out. Parameters for the conic projections
are distance to the projection area d
top
and d
bottom
,
rotation width α, rotation offset α
of f set
, and the height
of the conic given by Z
top
and Z
bottom
(see Figure 4(a)
and 4(b)). The cylindrical coordinates (α
P
,Z
P
)
T
of
a point P
F
at position [m, n]
T
in the target image are
then determined using equation (8)
~
P
F m,n
=
d
α
P
Z
P
with
d
α
P
Z
P
=
d
top
−
d
top
−d
bottom
N
· n
α
of f set
−
α
2
+
α
M
· m
Z
top
−
Z
top
−Z
bottom
N
· n
(8)
The carthesian coordinates (both for cylindrical and
conic projection) of every point are computed using a
standard coordinate transformation.
3.3 Spherical Projection
The projection area is a cut-out of a shperical surface.
Parameters for the spherical projections are the eleva-
tion width β, the elevation offset β
of f set
, the rotation
width α and rotation offset α
of f set
(see Figure 5(a)
and 5(b)). The spherical coordinates (α
P
,β
P
)
T
at po-
sition [m,n]
T
in the target image are calculated using
equation (9) (r = 1):
~
P
F m,n
=
r
α
P
β
P
=
r
α
of fset
−
α
2
+
α
M
· m
β
of fset
+
β
2
−
β
N
· n
(9)
The spherical coordinates are transformed into
carthesian coordinates using the rotation α
P
clock-
wise beginning at the y - axis and the elevation β
P
anti-clockwise beginning at the x axis.
X
Y
α
offset
α
α/2
P
α
P
(a) Top View
Y
Z
P
-β
P
β/2
β
-β
offset
(b) Side View
Figure 5: This figure shows the spherical projection param-
eters in top and side view.
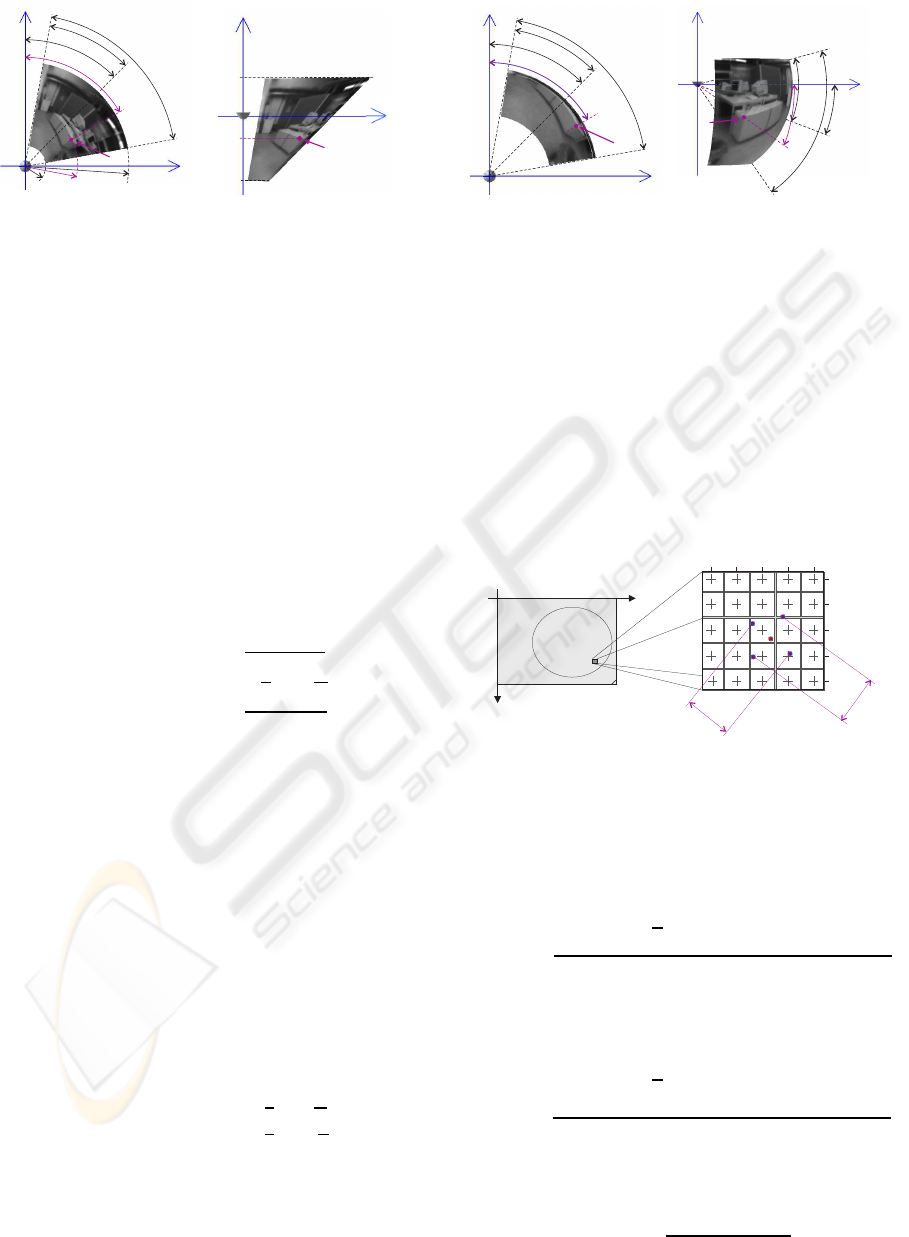
3.4 Pixel Density
To evaluate different projections and to compare dif-
ferent configurations of omnidirectional vision sen-
sors, the position dependent resolution of unwarped
images has to be calculated. Therefore, we propose
a novel value, the pixel density σ. To determine the
pixel density, the distances between pixels in rectified
images on the image sensor are determined. Figure 6
demonstrates the basic idea of the pixel density.
0
u
v
521 522 523 524 525
353
354
355
356
357
m,n
m-1,n
m+1,n
m,n+1
m,n-1
d
h
d
v
Figure 6: This figure shows the position of pixels in rectified
images on the image sensor (left) and its distances (right)
on the sensor plane, which are used to calculate the pixel
density.
The horizontal pixel density σ
h(m,n)
at position
[m,n]
T
is calculated using equation (10)
σ
h (m,n)
=
1
2
· d
h (m,n)
with (10)
d
h (m,n)
=
q
(u
(m+1,n)
− u
(m−1,n)
)
2
+ (v
(m+1,n)
− v
(m−1,n)
)
2
Analogical, the vertical pixel density σ
v(m,n)
at posi-
tion [m,n]
T
is defined as
σ
v (m,n)
=
1
2
· d
v (m,n)
with (11)
d
v (m,n)
=
q
(u
(m,n+1)
− u
(m,n−1)
)
2
+ (v
(m,n+1)
− v
(m,n−1)
)
2
The pixel density σ
g(m,n)
at position [m,n]
T
is defined
as the geometric mean (see equation (12)) of the hor-
izontal and vertical pixel densities
σ
g (m,n)
=
p
σ
h (m,n)
· σ
v (m,n)
(12)
IMAGE RECTIFICATION - Evaluation of Various Projections for Omnidirectional Vision Sensors using the Pixel Density
85

The pixel density σ characterises the consistence
of rectified image pixels with sensor pixels, which are
used for intensity calculation. Consequently, the pixel
density contains the resolution of rectified panoramic
images depending on the chosen projection and cam-
era setup. We assume, that best resolution reaches
rectified images achieving a pixel density nearly 1. A
pixel density less than 1 denotes poor resolution due
to less sensor pixels for one pixel in the rectified im-
age, while values larger than 1 denote good resolution
but wasting sensor pixels. The pixel density depends
on the camera, the choosen projection, the mirror con-
figuration including the curvature as well as the dis-
tance between projection center and pinhole.
4 EXPERIMENTAL RESULTS
To evaluate the projections proposed in section 3.1 to
3.3 as well as to analyse the properties of the pixel
density, images taken in a synthesised environment
and taken in our laboratory are used. The difference
between the characteristics of densities of real and
synthesised images was less than 0.3 pixels, so that
corresponding curves overlap. Therefore and for bet-
ter understanding, only synthesised images are pre-
sented and discussed. For both synthesised and real
Table 1: Overview of the tested parameters.
d (mm) k α (degree)
50 5,50 43,00
50 7,55 39,50
50 10,00 36,75
50 7,55 39,50
75 7,55 39,50
100 7,55 39,50
50 7,55 39,50
75 7,55 28,50
100 7,55 22,25
images, we designed various ODVS with different
curvatures (k), varying distances (d) between projec-
tion center and pinhole as well as diverse field of view
(FOV) (α) of the pinhole camera. Secondly, we define
a region of interest (ROI) for rectification, unwarp the
images using different projections and calculate the
pixel density. Table 1 gives an overwiev of the tested
parameters with constant ROI.
4.1 Rotational Symmetric Projections
using Synthetic Environments
First, we present the results of our measurements for
different distances d between the mirror projection
center and the pinhole (see section 4.1.1). Thereafter,
we present the characteristics of the pixel density de-
pending on the chosen projection using constant dis-
tances d (see section 4.1.2) and discuss the result in
section 4.2. The conic, cylindric and spheric projec-
tions are rotationally symmetric, so that the pixel den-
sity σ remains constant for all number of columns in
the rectified image.
(a) d=50mm, k=7.55 (b) d=75mm, k=7,55
Figure 7: This figure illustrates synthesised images ODVS
with constant k=7.55, d=50mm and d=75mm using the
same FOV.
4.1.1 Constant Mirror Type using Varying
Distances d as well as FOV
Figure 7 illustrates synthesised images from ODVS
with constant mirror type k=7.55 and different dis-
tances d=50mm and d=75mm using the same FOV.
Figure 8 shows also the same camera configuration
and the same mirror type, but the FOV is adapated to
get best utilisation of sensor pixels for image rectifi-
cation. The marked ROI (red) is used for rectification
as well as for calculation the pixel density.
(a) d=50mm, k=7.55 (b) d=100mm, k=7,55
Figure 8: An ODVS with the mirror constant k=7.55, dif-
ferent distances and an adapted FOV is used.
Figure 9 demonstrates the result using cylindrical
projection, while the characteristics of the pixel den-
sity depending on different distances, projections and
the chosen field of view (FOV) is presented in fig-
ure 10. The charts in the left column (10(a), 10(c),
10(e)) present the results using a constant FOV, while
the FOV in (10(b), 10(d), 10(f)) is adapted to get best
utilisation of sensor pixels.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
86

(a) d=50mm, k=7.55 (b) d=100mm, k=7,55
Figure 9: This figure shows unwarped images using cylin-
dric projection, the same mirror type k but different dis-
tances d.
(a) Const. α, k=7.55, cyl. (b) Var. α, k=7.55, cyl.
(c) Const. α, k=7.55, con. (d) Var. α, k=7.55, con.
(e) Const. α, k=7.55, sph. (f) Var. α, k=7.55, sph.
Figure 10: Pixel densities for ODVS’s with different dis-
tances d=50mm, d=75mm and d=100mm as well as fixed
FOV’s (left) and adapted FOV’s (right) using cylindrical,
conical and spherical projections.
4.1.2 Results from ODVS with SPOV using
Different k’s
To study the influence of the projection, images from
omnidirectional vision sensor with single point of
view and different mirror types k = 5,50, k = 7,55
and k = 10, 00 are generated. Figure 11 shows the
original images. We calculated the cylindric, the
conic and the spheric projection and rectified the im-
ages using LUT (see section 3).
The rectification result is illustrated in figure 12
for chosen mirror constants. Based on the rectified
images, the pixel density σ for each mirror and each
projection is determined. The characteristics of the
pixel density for the ODVS’s with SPOV for different
k’s illustrates figure 13.
(a) k=5.50 (b) k=7.55
(c) k=10.00
Figure 11: This figure illustrates synthesised images from
Single Point of View ODVS with different mirror types.
The marked ROI (red) is used for all rectifications.
(a) k=5.50, cylin-
dric
(b) k=5.50, conic (c) k=5.50, spheric
(d) k=7.55, cylin-
dric
(e) k=7.55, conic (f) k=7.55, spheric
(g) k=10.00, cylin-
dric
(h) k=10.00, conic (i) k=10.00,
spheric
Figure 12: The rectified images for a mirror constant k =
5.50, k = 7.55 k = 10.00 using cylindric, conic and spheric
projection.
4.2 Discussion
Figure 10 and figure 13 present the pixel densities
both for synthesised and real images. Measurements
show that differencesin the pixel density between real
and synthesised images were less than 0.3 pixels and
not significant. For a better understanding, only the
synthesised images are presented and discussed.
The pixel density depends on the ROI, the mirror
and camera configuration and the chosen projection.
For our studies, we use a ROI including regions under
the camera, with short and with large distances to the
ODVS. The best resolution reaches a rectified image
achieving a pixel density nearly 1. A pixel density
less than 1 denotes poor resolution in case of less sen-
sor pixels for one pixel in the rectified image, while a
IMAGE RECTIFICATION - Evaluation of Various Projections for Omnidirectional Vision Sensors using the Pixel Density
87

(a) k=5.50, SPOV (b) k=7.55, SPOV
(c) k=10.00, SPOV
Figure 13: The pixel densities for the different mirrors both
for the synthesised and the real rectified images are shown
in this diagram.
value larger than 1 denotes good resolution but wast-
ing sensor pixels.
In a first setup, the FOV of the camera remains con-
stant while the distance d between the mirro projec-
tion center and camera pinhole increases. As shown
in figure 10, the characteristics of pixel density (see
10(a), 10(c), 10(e)) descrease with larger distances d
by constant FOV’s because less sensor pixels can be
used for the light reflected by the mirror.
In a second setup, the FOV is adapted during increas-
ing of the distances d to get the best utilisation of sen-
sor pixels. If the FOV is adapted to the distances to
achieve good utilisation of sensor pixels for light re-
flected by the mirror, pixel density is nearly identical
for the same projection type. The small differences
as shown in figure (10(b), 10(d), 10(f)) result due to
the distance based variance of the vertical FOV. The
small differences also result of the increasing vision
field of the ODVS by increasing distances d. Figure
9(b) illustrates the larger field of view by the larger
distance d compared to 9(a).
In a third setup, we conduct experiments with differ-
ent projections as well as mirror configurations us-
ing cameras with a single point of view. As shown
in figure 13, the pixel density with constant sensor
resolution varies depending on the chosen projection.
The range of the pixel density for cylindrical projec-
tion varies in a large range between the upper and the
lower image area. The pixel density varies less for
the conical projection, therefore the sensor pixel are
mapped homogenous to the rectified image. The rec-
tified images using conic projection are the strongest
distorted images, but this need not to be a drawback.
A good compromis is the spherical projection with
less distortion and a nearly homogenous use of sensor
pixels in rectified images.
Figure 13 also demonstrates that the common cylin-
drical projection is not always the best projection for
image rectification due to the large range of the pixel
density characteristic. Furthermore, the variation of
pixel density for cylindric projection as shown in fig-
ure 10 and figure 10(b) is larger than the variation of
other projections for different distances between the
pinhole of camera and the mirror projection center.
To get best image quality of rectified images, the pro-
jection with least variance in the pixel density for
different mirrors as well as for various distances be-
tween camera pinhole and projection center is recom-
mended. If the distortion of rectified images is not a
problem for image processing routines, the conic pro-
jection seems to be the best projection due to less vari-
ances in the pixel density. Otherwise, the spherical
projection can be a good alternative. If only a small
region of interest in the projection area is needed for
image rectification (for example the area between 50
and 100 pixel (column)), the cylindrical projection
can also be a good choice for image rectification. So
the pixel density helps to find the projection with op-
timum use of sensor pixels in rectified images.
Using the LUT as proposed in section 3, online image
rectification is possible. Experiments show that only
6.5ms are necessary to transform images with a reso-
lution of 480 · 480 pixels to unwarped images with a
resolution of 540· 204 pixels on a 2.2 GHz AMD 64
X2 4200+ processor using bicubic interpolation.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we present methods to rectify and to un-
warp distorted images generated by omnidirectional
vision sensors (ODVS). Furthermore, we propose a
novel value, the pixel density, to evaluate different
projections.
The first step is to calibrate the camera providing a
relation between world and camera coordinates. Sec-
ondly, we present several projectionsand calculate the
projection area to transform original into panoramic
images using the calibrated camera model and a LUT
containing the world coordinates of every pixel in the
transformed region of interest. For our research, we
propose a novel value, the pixel density, to evaluate
the chosen projection to find best utilisation of sensor
pixels in rectified images.
To get best image quality of rectified images, the
projection type with least variance in the pixel density
both for different mirror types as well as for various
distances between the camera pinhole and the projec-
tion center is recommend. So the pixel density helps
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
88

to find the projection with optimum use of sensor pix-
els in rectified images.
Further studies of the pixel density and its relation to
the projections with different regions of interest (ROI)
are necessary. In the next step, the curvature of the
pixel density has to be parametrised to find a mathe-
matical relation between the pixel density and the pre-
sented projections.
ACKNOWLEDGEMENTS
The authors would like to thank Michelle Karg
and the reviewers for their comments which have
greatly improved the paper. Support for this re-
search was provided by BMW AG in the framework
of CAR@TUM.
REFERENCES
Baker, S. and Nayar, S. K. (1999). A theory of single-
viewpoint catadioptric image formation. International
Journal of Computer Vision, 35(2):175–196.
Baker, S. and Nayar, S. (2001). Single viewpoint catadiop-
tric cameras. Monographs in Computer Science.
Colombo, A., Matteucci, M., and Sorrenti, D. G. (2007).
On the calibration of non single viewpoint catadiop-
tric sensors. Lecture Notes in Computer Science,
Springer, pages 194–205.
Daniilidis, K. and Geyer, C. (2000). Omnidirectional vi-
sion: Theory and algorithms. In Proceedings of the
XV International Conference on Pattern Recognition.
Gandhi, T. and Trivedi, M. M. (2004). Motion analysis for
event detection and tracking with a mobile omnidirec-
tional camera. Multimedia Systems, 10(2):1432–1882.
Gaspar, J., Decco, C., Okamoto, J., and Santos-Victor, J.
(2002). Constant resolution omnidirectional cameras.
In Proceedings of the Third Workshop on Omnidirec-
tional Vision.
Geyer, C. and Daniilidis, K. (2001). Catadioptric projective
geometry. International Journal of Computervision,
45(3):223–243.
Hicks, R. and Perline, R. (2002). Equi-areal catadioptric
sensors. In Proceedings of the Third Workshop on
Omnidirectional Vision.
Ishiguro, H. (1998). Development of low-cost compact om-
nidirectional vision sensors and their applications. In
Proceedings of the International Conference on Infor-
mation Systems, Analysis and Synthesis.
Krishnan, A. and Ahuja, N. (1996). Panoramic image ac-
quisition. In Proceedings of the IEEE Conference on
Computervision and Pattern Recognition.
Mei, C. and Rives, P. (2007). Single view point omni-
directional camera calibration from planar grids. In
Proceedings of the IEEE International Conference on
Robotics and Automation.
Micusik, B. and Pajdla, T. (2004). Para catadioptric camera
auto-calibration from epipolar geometry. In Proceed-
ings of the 6th Asian Conference on Computer Vision
System.
Scaramuzza, D., Martinelli, A., and Siegwart, R. (2006a). A
flexible technique for accurate omnidirectional omni-
directional camera calibration and structure from mo-
tion. In Proceedings of the Fourth IEEE Conference
on Computer Vision Systems.
Scaramuzza, D., Martinelli, A., and Siegwart, R. (2006b).
A toolbox for easily calibration omnidirectional cam-
eras. In Proceedings of the IEEE/RSJ International
Conference on Intelligent Robots and Systems.
Utsumi, A., Mori, H., Ohya, J., and Yachida, M. (1998).
Multiple-view-based tracking of multiple humans. In
Proceedings of the IEEE Conference on Computervi-
sion and Pattern Recognition.
Yamazawa, K., Yagi, Y., and Yachida, M. (1993). Om-
nidirectional imaging with hyperboloidal projection.
In Proceedings of the IEEE/RSJ International Confer-
ence on Intelligent Robots and Systems.
Yamazawa, K., Yagi, Y., and Yachida, M. (1998). Hy-
peromni vision: Visual navigation with an omnidirec-
tional image sensor. Systems and Computers in Japan,
28:36–47.
IMAGE RECTIFICATION - Evaluation of Various Projections for Omnidirectional Vision Sensors using the Pixel Density
89
