EFFICIENT PLANAR CAMERA CALIBRATION VIA AUTOMATIC

IMAGE SELECTION

Brendan P. Byrne, John Mallon and Paul F. Whelan

Centre for Image Processing & Analysis,

Dublin City University, Dublin 9, Ireland

Keywords:

Planar camera calibration, Image network, Automatic image selection.

Abstract:

This paper details a novel approach to automatically selecting images which improve camera calibration re-

sults. An algorithm is presented which identiﬁes calibration images that inherently improve camera parameter

estimates based on their geometric conﬁguration or image network geometry. Analysing images in a more

intuitive geometric framework allows image networks to be formed based on the relationship between their

world to image homographies. Geometrically, it is equivalent to enforcing maximum independence between

calibration images, this ensures accuracy and stability when solving the planar calibration equations. A we-

bcam application using the proposed strategy is presented. This demonstrates that careful consideration of

image network geometry, which has largely been neglected within the community, can yield more accurate

parameter estimates with less images.

1 INTRODUCTION

Camera calibration from planar targets is the domi-

nant conﬁguration when working with conventional

perspective cameras. Its foundations were proposed

independently by Sturm and Zhang (Sturm and May-

bank, 1999; Zhang, 1999) and are well understood

within the community today. Compared with tradi-

tional calibration techniques (Faugeras, 1993; Tsai,

1987; Wei and Ma, 1994), plane based calibration sig-

niﬁcantly reduces input data requirements. This cou-

pled with readily available implementations, (Bouget,

2001; OpenCV, 2001), has contributed to its popular-

ity.

Planar calibration simply requires the user to cap-

ture at least two images with varying planar target

pose. We call these images the image network (IN).

Typically many more images are used to improve cal-

ibration accuracy. The stability of planar calibration

methods has been well studied in the literature (Gon-

zalez et al., 2005; Salvi et al., 2002; Sun and Cooper-

stock, 2007). Generally the stability is characterised

based on the reprojection error which is the Euclidean

distance between the 3D world points, back projected

onto the image plane, and the measured 2D image

points. In all cases ﬁndings suggest that larger INs

increase parameter estimation accuracy.

Although large INs yield more accurate results,

practical constraints such as capturing a large data

set, feature extraction, and calibration takes a consid-

erable amount of time and expertise. To this end it

would be desirable to achieve good calibration accu-

racy within these practical constraints. Thus the focus

should be on forming smaller INs capable of produc-

ing accurate results. This paper outlines how this is

achieved via automatic image selection (or a Selected

Image Network (SIN)).

The possibility of degeneracies increases when

considering a smaller image set. The degeneracies

effect the conditioning of the planar calibration equa-

tions and lead to poor parameter estimates. Critical

conﬁgurations have been identiﬁed and well studied

by (Sturm and Maybank, 1999) and (Zhang, 1999)

and shown to consist of pure rotation and translation,

butimages close to critical, which are difﬁcult to iden-

tify and havereceived less attention in the community,

also give poor results.

In (Rupp and Elter, 2007), an image selection

strategy is employed to improve calibration results.

However, the algorithm selects images based on their

reprojectionerror which requires the camera to be cal-

ibrated in the ﬁrst place. This defeats the purpose of

an efﬁcient calibration via image selection and adds

considerable time and effort in doing so. Also, by us-

P. Byrne B., Mallon J. and F. Whelan P. (2009).

EFFICIENT PLANAR CAMERA CALIBRATION VIA AUTOMATIC IMAGE SELECTION.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 90-94

DOI: 10.5220/0001792100900094

 SciTePress

ing the reprojection error as a quality measure, image

and camera noise may effect results as images with

favorable geometry could be omitted. By analysing

the planar calibration problem in an alternative geo-

metric framework as proposed by (Gurdjos, 2001) it

is possible to form a geometric criterion for selecting

good calibration images which does not require a pre-

calibration stage.

The main contribution of this work is that it pro-

vides an image selection algorithm, based on an al-

ternativegeometric interpretation, which forms image

networks (SINs) that contain less images and give ef-

ﬁcient calibration results. An application using a we-

bcam is presented which demonstrates that efﬁcient

calibration results can be achieved with little effort.

2 METHOD

The proposed algorithm selects images based on char-

acteristics from the alternative geometric approach

proposed by (Gurdjos, 2001). In Figure 1, as the

world plane rotates about its intersection with the im-

age plane it remains in homographic correspondence.

Thus a single planar homography matrix H represents

the transformation. The associated camera centres, of

each rotating world to image plane, forms a locus of

possible camera centres which in turn projects to the

image plane in the form of a line, the Calibration Line

(CL). By using the well known (Sturm and Maybank,

Figure 1: Poncelet’s Theorem (Gurdjos, 2001).

1999; Zhang, 1999) planar calibration equations con-

straints (1), and following some algebraic manipula-

tions, an expression for the CL can be derived (2).

ωh

− h

ωh

= 0, h

ωh

= 0 (1)

where h

is the i

column of H.

= Γu

+ Λ (2)

where Γ is the slope of the CL given by,

Γ =

−h

+ h

− h

+ h

− h

+ h

(3)

and Λ is the y-intercept given by,

Λ =

+ h

−

+ h

Γ (4)

In (Wang and Liu, 2006), the authors propose a

method of linear calibration using the intersection

point of CLs. In our method we use the CLs as a guide

to choosing calibration images for the SINs. Suit-

able images are selected based on the orientation of

their CLs. Since the CL encapsulates geometric infor-

mation about the planar grid in the world, enforcing

maximum independence between CLs ensures each

image contributes independently to solving the sys-

tem of planar calibration equations. Independence be-

tween images is evaluated based on the relative angle

between image CLs. The angle between CLs, (θ), is

dependant on the number of images in the IN (N).

θ =

180

◦

(5)

Therefore if a four IN is required from a data set the

angle between image CLs should be 45

◦

. In practice,

a tolerance of ±1

◦

is enforced on θ for the selection

process. Based on the homographies from multiple

images, we employ an algorithm to select the most

suitable images which will provide efﬁcient calibra-

tion results.

3 IMAGE SELECTION

Automatic image selection is implemented in two

stages. The initial step requires each image CL to be

formed (as in section 2) with the angle of each CL rel-

ative to the x-axis calculated via the slope (arctan(Γ)).

CLs that have absolute angle near 0

◦

or 90

◦

are re-

jected for consideration as they correspond to unsta-

ble IN geometry (fronto-parallel). Once N is chosen

the optimal θ can be calculated (5) which is used to

form the SINs.

The underlying search method of the proposed

image selection strategy is a binary search approach

(Knuth, 1998). In Figure 2 the proposed strategy is

presented. Each node represents an image number

while the number adjacent to each node is its CL ori-

entation. In a real situation all nodes are connected

to each other where the connecting lines represent the

angle between image CLs. To aid explanation all pos-

sible connecting lines are not shown, instead the valid

search paths are shown i.e each line is in fact equal to

the binary search key which is |θ| ± 1

In this example, N, the number of images required

in the SIN, is set to four therefore θ is 45

◦

. The

search begins with the seed node 1. When a route

EFFICIENT PLANAR CAMERA CALIBRATION VIA AUTOMATIC IMAGE SELECTION

corresponding to the search key is identiﬁed (node

3) the search continues with node 3 as the seed. In

this case there are two possible routes, node 12 and

17. Since a binary search exploits only one route at a

time, the proposed strategy implements the search in

a cascaded fashion. Therefore the search will return

to this point and follow other routes in the next cy-

cle. If node 12 is chosen there are three candidates to

form the SIN - 22, 31 and 64. When one possibility

is chosen the SIN is formed and the node is deleted.

This will allow the binary search to ﬁnd the next valid

IN with subsequent searches. When all possible SINs

along the (1, 3, 12) route have been formed, all image

nodes are reintroduced but node 12 is deleted. This

enables the algorithm to return to the point (1, 3) and

follow route 17. The search continues in this fashion

until all valid routes have been identiﬁed.

1

3

12

17

22

31

64

-25

20

64

65

-70

-69

-71

Tier 1

Tier 2

Tier 3

Tier 4

Figure 2: Image Search Space.

3.1 Search Algorithm Implementation

The implementation of the search algorithm is pre-

sented in Figure 3. The algorithm is initialised with

the seed node which is stored in the IN matrix. The

binary search is implemented and if it’s successful,

the current IN size, N

, is incremented and the image

found, imt, is stored in IN. A check is performed to see

if N

is equal to N the desired IN size. If true the cur-

rent imt is deleted from the search space and the algo-

rithm loops back to run the binary search again. This

is a similar situation as in Figure 2 when tier 4 was

reached, the node was deleted so other nodes could

be found in subsequent searches. In the case where

6= N, the algortihm simply loops back to ﬁnd the

next image in the network via the binary search.

The most signiﬁcant branch point in the algorithm

is the binary search junction. When a search fails it in-

dicates that there are no more routes in a particular tier

of the search space. A check is performed on N

see if the search has failed in tier 2 (i.e. if N

= 1). If

it has failed the overall search is ﬁnished and all valid

INs are stored in the IN matrix. On the other hand, if

6= 1, all nodes are reintroduced to the search space

and the N

node of the current IN is deleted from the

list. This is a similar situation to the example given

in Figure 2 where the IN was (1, 3, 12). When all tier

4 nodes were found and subsequently deleted, node

12 was removed which allowed the binary search to

follow the (1, 3, 17) route. The search continues until

= 1 which indicates that all possible routes have

been explored. The algorithm is implemented in this

fashion for each node in the search space. Further re-

ﬁnement can be applied to the algorithm if duplicate

INs are stored.

Initialise

IN = [IN im]

BS fail?

N = N + 1

IN=[IN imt];

T T

N = N?

T

N = 1?

Load nodes,

delete N from list

and current IN

th

delete imt

no

yes

no

Finish

Store IN

no

yes

imt : image returned (BS)

BS : Binary search

IN : Image Network

im : Initial image

N : Desired IN size

N : Current IN size

T

Figure 3: Algorithm Flowchart.

4 APPLICATION

A webcam calibration application was developed

to demonstrate the beneﬁts of the image selection

scheme. A labtec “web” webcam capturing 15fps at

320 × 240 pixels was used. The application captures

images for 20 seconds thus giving 300 images for the

calibration data set. Images are captured, by vary-

ing the location of the camera, while also ensuring

the planar calibration target remains within the ﬁeld

of view of the webcam. OpenCV is used to extract

the planar pattern corners from each frame to subpixel

accuracy. The homographies are calculated for each

frame followed by implementation of the proposed

image selection algorithm to identify the SINs. The

planar calibration method of (Zhang, 1999) is used to

verify results.

5 RESULTS

Validation of the SINs is performed by comparison

with randomly drawn INs from the data set. Random

INs (RIN) are used as there are no speciﬁc methods

to compare with currently in the literature. Three ex-

periments are conducted to illustrate the calibration

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

accuracy and overall beneﬁt of using SINs. The ﬁrst

experiment examines the accuracy of the calibration

result as the number of views increases. This is fol-

lowed by a rigorous comparison of the IN conﬁgura-

tions with less images. The ﬁnal experiment validates

the calibration accuracy of SINs by analysing the lens

distortion in the images. As there is no ground truth

a calibration result is calculated using all 300 frames

and used as an indicative optimal result for compari-

son.

5.1 Convergence of Image Networks

This experiment examines the accuracy of the cali-

bration result as the number of images in the IN in-

creases. The results are given in terms of percentage

error for each calibration result. For each image net-

work instance (2 to 25 INs) ten SINs are compared

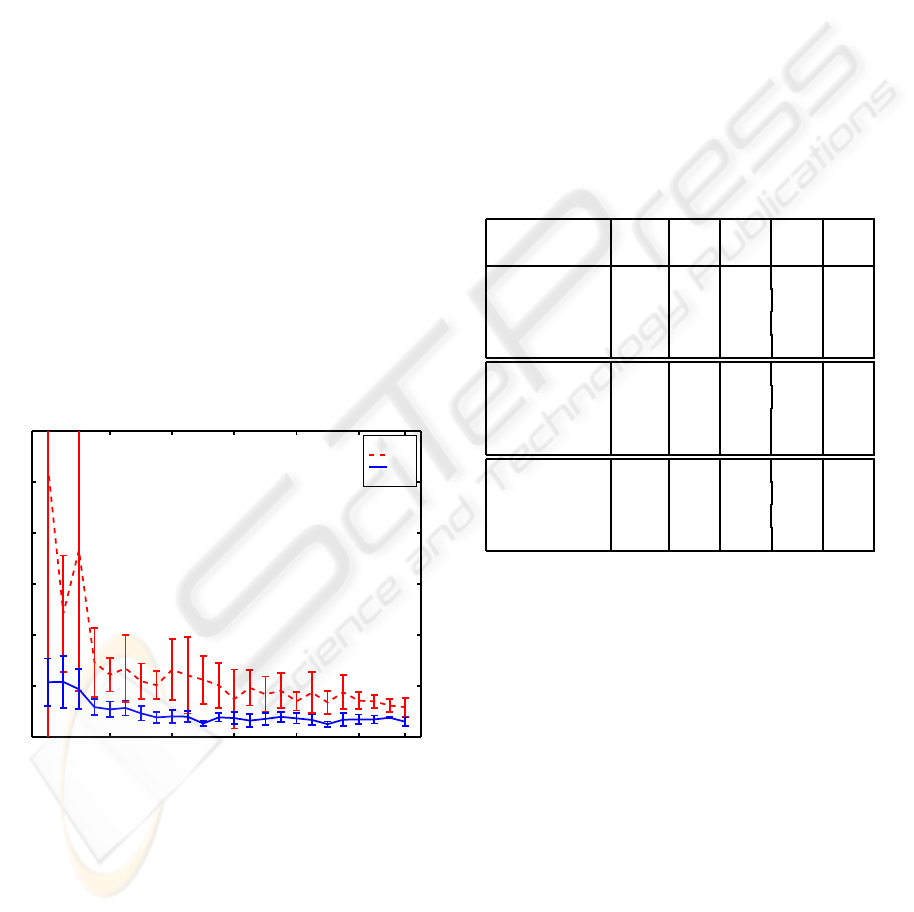
with ten RINs from the data set. From Figure 4, it is

evident that the SINs produce more accurate and re-

liable calibration results than the RINs, especially for

the smaller INs. As the number of views increases

the stability of the SIN results clearly outperform the

RINs. The most signiﬁcant result here is that less im-

ages are needed to achieve accurate calibration results

when SINs are used. The following experiment exam-

ines this in more detail.

2 6 10 14 18 22 25

Convergence of SIN v RIN

# Views

Calibration Pixel Error (%)

RIN

SIN

Figure 4: Calibration accuracy as the number of views in-

creases from 2 to 25 INs. Standard deviation is represented

by bars at each IN instance.

5.2 Reduced Number of Images

The number of images for each IN conﬁguration is

reduced for this set of experiments to validate the pre-

vious results which identiﬁed that SINs can achieve

more accurate results than the RINs with less images.

All results in Table 1 are given in terms of percentage

error with respect to the indicative optimal calibration

results. There are 50 two INs, 30 three and 25 four

INs in the SIN cases of Table 1. The RINs consist of

2500 randomly drawn image combinations for each

IN size. This consisted of 50 trials of 50 IN instances

for each test. This insured that a wide range of RINs

were compared for the results.

The results in Table 1 indicate that the SINs sig-

niﬁcantly outperform the RINs. This is due to the

geometry of the SINs, which avoid degenerate con-

ﬁgurations, and also have favorable image geometry

for solving the calibration equations more efﬁciently.

This is a signiﬁcant result in terms of the input re-

quirements for planar camera calibration, by exploit-

ing geometric properties of the images, less input im-

ages are needed to achieve accurate calibration re-

sults.

Table 1: Image Network Conﬁguration Comparison.

Image Network No. fx fy u v

Consensus Images ¯x (σ) ¯x (σ) ¯x (σ) ¯x (σ)

Random 2 23.3 20.7 23.7 23.5

(41.1)(31.5)(44.6)(27.1)

SIN 2 11.5 11.1 13.3 24.1

(11.7)(11.7)(16.6)(26.5)

Random 3 20.2 20.5 24.2 25.1

(30.6)(30.7)(31.4)(31.5)

SIN 3 3.8 3.6 5.3 9.9

(3.9) (4.3) (7.5) (7.9)

Random 4 8.9 8.9 10.8 11.1

(21.1)(21.1)(22.9)(19.4)

SIN 4 1.59 1.49 2.74 3.88

(1.55)(1.69)(3.31)(3.32)

5.3 Distortion Correction

This experiment further justiﬁes the use of the SINs

by analysing distortion in the images. The beneﬁt

of un-distorting the images is that the canonical cali-

bration plane is used as ground truth which gives the

distortion correction residuals. Calibration results us-

ing two INs is used for this experiment since it is

the minimum case for solving planar calibration. The

plots in Figure 5 represent the error vectors of the un-

distortion estimation (scaled by 20 for plots). The

SINs have removed most radial distortion from the

image (mean residual 0.2 pixels) whereas the random

network still has signiﬁcant distortion present (mean

residual 0.39 pixels).

EFFICIENT PLANAR CAMERA CALIBRATION VIA AUTOMATIC IMAGE SELECTION

100 150 200 250 300

100

150

Random 2 Image Network

100 150 200 250

100

150

Filtered 2 Image Network

Figure 5: Residuals after un-distortion stage (in pixels).

6 CONCLUSIONS

This paper has presented a new approach to choosing

planar calibration images which give accurate calibra-

tion results. This is accomplished by considering ge-

ometric aspects of images in the form of the CL and

thus forming selected image networks (SINs). Unlike

previous image selection methods it does not require a

pre-calibration stage, it simply takes the image set and

calibrates based on the image CLs. This ensures inde-

pendence in the calibration images and avoids degen-

erate conﬁgurations. Experimentation has shown that

less input images are needed to achieve efﬁcient re-

sults using SINs. The application presented also pro-

vides a simple means of achieving accurate results for

non-expert practitioners, as the only input needed is

varying the camera location while capturing the im-

ages.

ACKNOWLEDGEMENTS

This research is funded by the Irish Research Council

for Science, Engineering and Technology: funded by

the National Development Plan.

REFERENCES

Bouget, J. (2001). www.vision.caltech.edu/bouguetj/calib.

Faugeras, O. (1993). Three Dimensional Computer Vision:

A geometric Viewpoint. MIT Press.

Gonzalez, J. I., Gmez, J. C., Artal, C. G., and Cabrera, A. N.

(2005). Comparative analysis of calibration methods

for a static camera. WAF05.

Gurdjos, P. (2001). Calibration of a moving camera using a

planar pattern: A centre line-based approach for vary-

ing focal length. In BMVC.

Knuth, D. E. (1998). The Art of Computer Programming,

volume 3. Addison-Wesley, second edition.

OpenCV (2001). intel.com/technology/computing/opencv.

Rupp, S. and Elter, M. (2007). Robust camera calibration -a

generic, optimization-based approach. In VISAPP07.

Salvi, J., Armangue, X., and Batlle, J. (2002). A compara-

tive review of camera calibrating methods with accu-

racy evaluation. Pattern Recognition, 35(7).

Sturm, P. and Maybank, S. (1999). On plane-based camera

calibration: A general algorithm, singularities, appli-

cations. In CVPR99.

Sun, W. and Cooperstock, J. (2007). An empirical evalua-

tion of factors inﬂuencing camera calibration accuracy

using three publicly available techniques. MVA.

Tsai, R. (1987). A versatile camera calibration technique for

high-accuracy 3d machine vision metrology using off-

the-shelf tv cameras and lenses. RA, 3(4):323–344.

Wang, J. and Liu, Y. (2006). Characteristic line of planar

homography matrix and its applications in camera cal-

ibration. icpr, 1:147–150.

Wei, G. and Ma, S. (1994). Implicit and explicit camera

calibration: Theory and experiments. PAMI, 16(5).

Zhang, Z. (1999). Flexible camera calibration by viewing a

plane from unknown orientations. In ICCV99.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications