3D PHASE CORRELATION USING NON-UNIFORM CYLINDRICAL

SAMPLING

Jakub Bican and Jan Flusser

Institute of Information Theory and Automation, Pod vod´arenskou vˇeˇz´ı 4, 18208 Prague 8, Czech Republic

Faculty of Mathematics and Physics, Charles University in Prague, Ke Karlovu 3, 121 16 Prague 2, Czech Republic

Keywords:

Image registration, Phase correlation, Cylindrical transform, Rigid-body transform, Experiments.

Abstract:

A Phase Correlation Method (PCM) is a well known and effective strategy for 2D image registration. Earlier

we presented a derived method called Cylindrical Phase Correlation Method (CPCM) which belongs among

many improvements and applications of PCM published by other authors. CPCM utilizes the effective and

robust approach of PCM for a 3D image rigid registration task in an iterative optimization procedure. In this

paper, the improvement to the rotation estimation step based on the non-uniform sampling in the cylindrical

coordinate system is described in detail. Experimental results are provided both for the original and improved

version of the rotation estimation algorithm as well as the results of the ﬁnal method and its comparison to

reference methods.

1 INTRODUCTION

Rigid body registration task is a very important area

in the space of image registration methods (Zitov´a

and Flusser, 2003). The purpose of rigid body reg-

istration algorithms is to spatially align a pair of im-

ages mutually rotated and translated. This is often a

case in medical image registration: the images of rigid

parts of human body (especially head) taken at differ-

ent times are aligned to detect the changes across the

time.

The presented method – Cylindrical Phase Cor-

relation (CPCM) introduced in (Bican and Flusser,

2007) – is a 3D rigid body registration algorithm that

ﬁts into a family of optimization methods that aim to

ﬁnd an extreme of similarity or dissimilarity measure

on a multidimensional space of parameters of a se-

lected transform model by some numerical optimiza-

tion process (Zitov´a and Flusser, 2003). CPCM is

based on a Phase Correlation Method (PCM) ﬁrst in-

troduced by (Kuglin and Hines, 1975) as a fast and

robust method for estimation of inter-image shifts.

PCM was extended by (De Castro and Morandi,

1987) to register translated and rotated images and

later by (Reddy and Chatterji, 1996) to register trans-

lated, rotated and scaled images. All of the refer-

enced approaches process 2D images, while (Keller

et al., 2006) introduced an algorithm for the registra-

tion of rotated and translated 3D volumes based on

Pseudopolar Fourier transform. Their approach uses

the pseudopolar representation of spectral magnitudes

to ﬁnd the rotation axis and estimate the rotation angle

without using interpolation. More details to the back-

ground of CPCM can be found in (Bican and Flusser,

2007).

In this paper, we describe in detail the rotation

estimation improvement ﬁrst laid out in (Bican and

Flusser, 2007). The improvement is based on the non-

uniform sampling in the cylindrical coordinate space

and therefore reduces the non-uniformity of the stan-

dard cylindrical approach with respect to the original

orthogonal grid. We also provide an experimental ex-

amination of the improvement.

2 METHOD OVERVIEW

Rigid body transform is a transform that combines

rotations and translations. Finding optimal parame-

ters of rigid body transform (six parameters in 3D)

is a very usual task of image registration (Zitov´a and

Flusser, 2003) (intra-subject studies, multimodal reg-

istration, etc). As it was mentioned in the introduc-

tion, there is a class of registration methods that em-

ploy a numerical optimization process to ﬁnd the op-

timum of similarity measure on a space of parame-

ters of a transformation model. Our algorithm uses

254

Bican J. and Flusser J. (2009).

3D PHASE CORRELATION USING NON-UNIFORM CYLINDRICAL SAMPLING.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 254-258

DOI: 10.5220/0001792502540258

 SciTePress

below described procedures of translation estimation

and rotation estimation to ﬁnd parameters of rigid

body transform so that the PCM metric – the correla-

tion of whitened images – reaches its maximum. The

optimization runs in iterations. Each iteration aims

to improve the measure with respect to some sub-

set of parameters. Such optimization resembles some

well known optimizers – e.g. Powell’s direction set

method (Press et al., 1992) – and is sometimes called

alternating optimization.

The algorithm starts with identity transform T and

a set of three linear independent axes (e.g. x, y and z).

In each iteration, a transform update T

upd

is computed

and merged with actual transform: T ← T ◦T

upd

. This

iterative process is stopped if there was no non-zero

update found in last six iterations (no transform pa-

rameter can be further optimized), or if the maximum

number of iterations is met (time limit) or if the actual

result is good enough (e.g. algorithm is stopped by an

operator).

2.1 Odd Iterations: Translation

Estimation

The translation estimation steps are based clearly

on Phase correlation method by (Kuglin and Hines,

1975). PCM takes advantage of Fourier shift theorem

that relates the phase information of spectrums of a

reference image f

and its shifted copy. If moving

image f

is the shifted copy of f

then the inverse

Fourier transform of so-called cross-power spectrum

forms a correlation surface corr – i.e. a correlation

value (of whitened images) for all possible discrete

shifts:

corr(

ω) = F

−1



∗

||F



. (1)

Thus, locating a peak in a correlation surface corr

results in offset ∆~x that can be used to align f

and f

at pixel level:

PCM( f

, f

) = ∆~x = argmax

(corr(~x)) ,

upd

← PCM( f

,T ( f

)) .

(2)

2.2 Even Iterations: Rotation

Estimation

In 2D, the rotations around a ﬁxed centre may be

estimated by the PCM method executed on polar-

transformed images (De Castro and Morandi, 1987).

In the same way how polar transform converts rota-

tions to translations in 2D, the cylindrical transform

may be used to convert rotation around ﬁxed axis to a

translation in 3D.

Let’s represent the rotation by axis ~v and angle α

and assume that the rotation axis~v is known. For sim-

plicity suppose, that the rotation axis is the z axis of

the Cartesian coordinate system. Transformation to

cylindrical coordinates about z axis is computed as

∗z

(α,r,z) = f (rcosα,rsinα,z). Rotation of image

by angle ∆α has the same effect as shifting the pe-

riodically extended image f

∗z

by ∆~x

∗z

= (∆α, 0,0)

(~x) = f

(∆α)~x) ,

∗z

(~x

∗z

) = f

∗z



(~x

∗z

+ ∆~x

∗z

) mod S

∗z



(3)

where R

(∆α) is the rotation matrix for rotation about

z axis (Baker, 2007) and S

∗

is the size of image f

∗

(Asterisk superscript (

∗z

) denotes here the cylindrical

coordinate system with axis z.)

Now it is clear that the rotation angle ∆α can be

estimated by PCM on cylindrically transformed im-

ages f

∗

and f

∗

upd

← PCM



∗z

,T ( f

)

∗z



. (4)

Axes cyclically alternate as the algorithm ad-

vances so that for example in iterations 2,4,6,8,10.. .

are used axes x,y,z,x, y... respectively.

3 ROTATION ESTIMATION

IMPROVEMENT

The approach described in previous section has two

main drawbacks. The ﬁrst one is caused by perform-

ing computations in discrete domain: when making

cylindrical transform of the images, it is necessary to

use higher order interpolation, because the cylindri-

cal transform (alike a polar transform) is sampling the

space very non-uniformly.

The second drawback is that the voxels of origi-

nal volume located near the axis of the cylinder have

much greater impact than the voxels located at the

perimeter. If the angular and radial coordinate is sam-

pled so that the perimeter of the cylinder is not sub-

sampled and no information is lost, every voxel near

the axis is stretched (or interpolated) to several vox-

els, while the voxels at the perimeter are resampled

approximately one-to-one. Moreover, the PCM gives

the same signiﬁcance to well sampled voxels at the

perimeter as to resampled voxels originating from the

voxels near the axis, which are also highly affected by

interpolation error.

These drawbacks led us to develop technique

which computes PCM separately for every layer of

the cylinder deﬁned by ﬁxed radius. Every such layer

has different angular resolution that suitably samples

3D PHASE CORRELATION USING NON-UNIFORM CYLINDRICAL SAMPLING

255

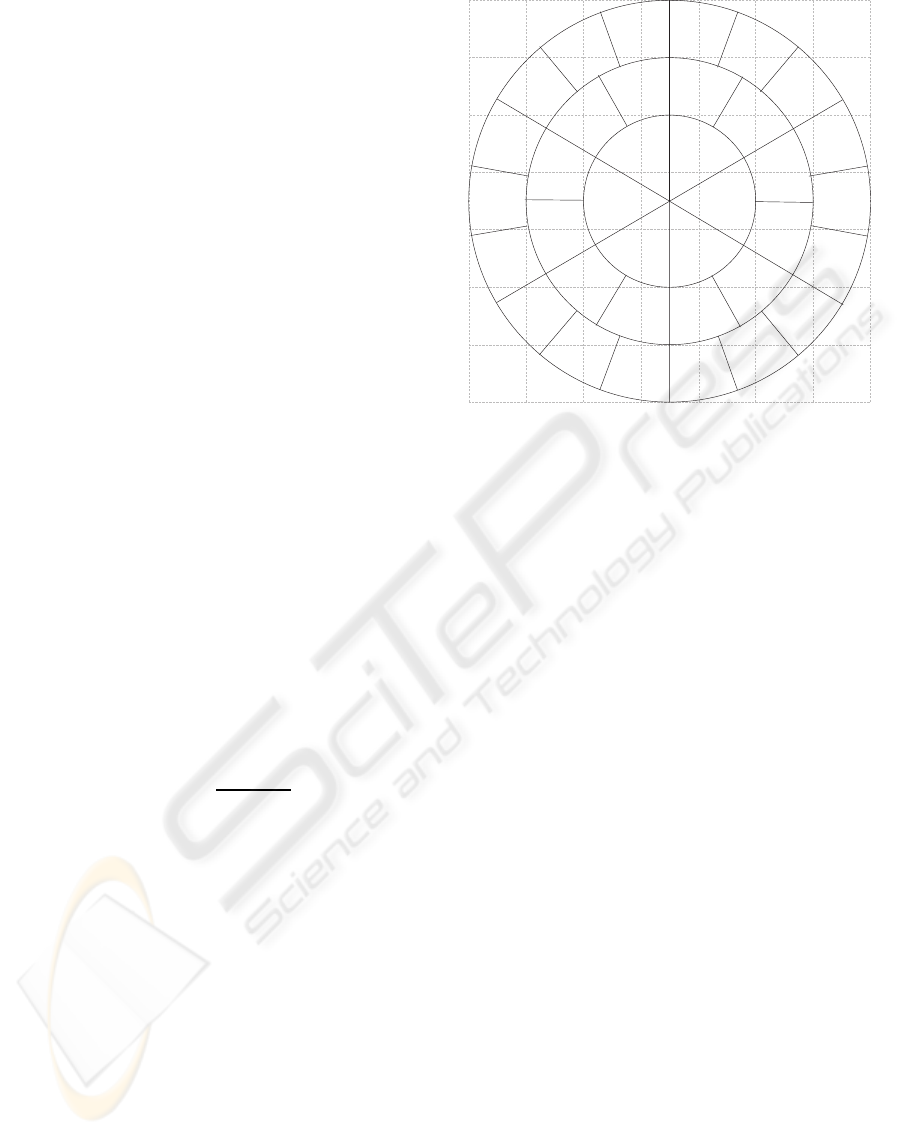
the original data: layer at radius r is in angular di-

rection sampled by 2πr samples, i.e. with resolution

(spacing) 2π/2πr = 1/r radians.

(α,z) = f

∗

(α,r,z) ∀α = 0,1/r,. ..,(2π − 1)/r

∀z = 0,1,. ..,S

∗

(5)

Such sampling is a result of an effort to have the pix-

els approximately the same size in all layers and in the

original orthogonal grid. The r value is determined as

the spacing value in simple case (if the sampling of

the original data is the same in each direction) or as

the minimum (to preserve all data), maximum (to save

memory resources), average or some other computed

value of the spacings in all directions of the original

data. Therefore the cylindrical pixels are r wide and

r long. Figure 1 displays the sampling in the simple

case. The maximum r may be also determined in dif-

ferent ways. In this paper, we use r as the half of

the maximum size of the data across all dimensions,

so we make an inner envelope in case the data have

the same size in all dimensions, and therefore we use

something between inner and outer envelope if this

does not apply. In ideal case, the region-of-interest

should be detected and included whole in the cylin-

der. Similar considerations apply also for the height

of the cylinder z (we use 2r

max

Corresponding layers from reference and moving

image are registered by PCM which results in a cor-

relation surface that gives a degree of match for each

angle. Correlation surfaces from all layers are then

summed to get the global correlation surface

corr

imp

(α,z) =

∗

∑

r=1

−1



∗

||L



(α,z) , (6)

where L

R|M

are Fourier transforms of layers l

R|M

Each layer is weighted by its radius r which corre-

sponds to the number of pixels it contains. This gives

to each original voxel same impact on the result.

Off-grid image values in equation (5) are com-

puted using linear interpolation. Off-grid layer cor-

relation surface values in equation (6) are computed

using nearest-neighbour interpolation. Finally, posi-

tion of the highest peak in the combined correlation

surface corr

imp

gives the ﬁnal result of the registration

IRE( f

, f

) = argmax

α,z



corr

imp

(α,z)



. (7)

We call this algorithm improved rotation estima-

tion and use it in the even iterations of CPCM to esti-

mate the rotation. A comparison with basic version of

the rotation estimation algorithm is shown in experi-

mental part of the paper.

Figure 1: An example of the sampling approach in the im-

proved version of the rotation estimation algorithm. Each

layer of the cylinder is sampled with appropriate resolution.

The ﬁrst three layers of pixels of improved cylindrical sam-

pling are displayed on top of regular orthogonal pixel grid.

4 EXPERIMENTAL RESULTS

In this section, we present outputs of some exper-

iments that have been done to examine the perfor-

mance of the CPCM method. First, the results of the

whole method are reviewed, as they were published in

(Bican and Flusser, 2007). Second, the improved ver-

sion of the rotation estimation algorithm is examined

and compared with the basic version.

In the experiments and results below, the sizes

and distances are presented in millimetres as the usual

medical volumetric data have different spacing (sam-

pling, voxel size) in each dimension. To relate the

presented distances with the voxel grid, see the cap-

tion of the appropriate ﬁgure presenting the data.

4.1 3D Rigid Registration Performance

In the ﬁrst experiment, whole CPCM method in-

cluding the improvement is examined. We use the

method to register randomly rotated and shifted real

MRI brain image (volume size is 128×128× 40 with

1.8× 1.8× 4.58 mm spacing) with the original. The

degree of misregistration as well as the registration

error is measured by a ﬁxed set of eight points that

uniformly sample the reference image’s volume. The

error (or misregistration) is then measured as a mean

Euclidean distance of these points in moving image

to their original counterparts in reference image. This

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

256

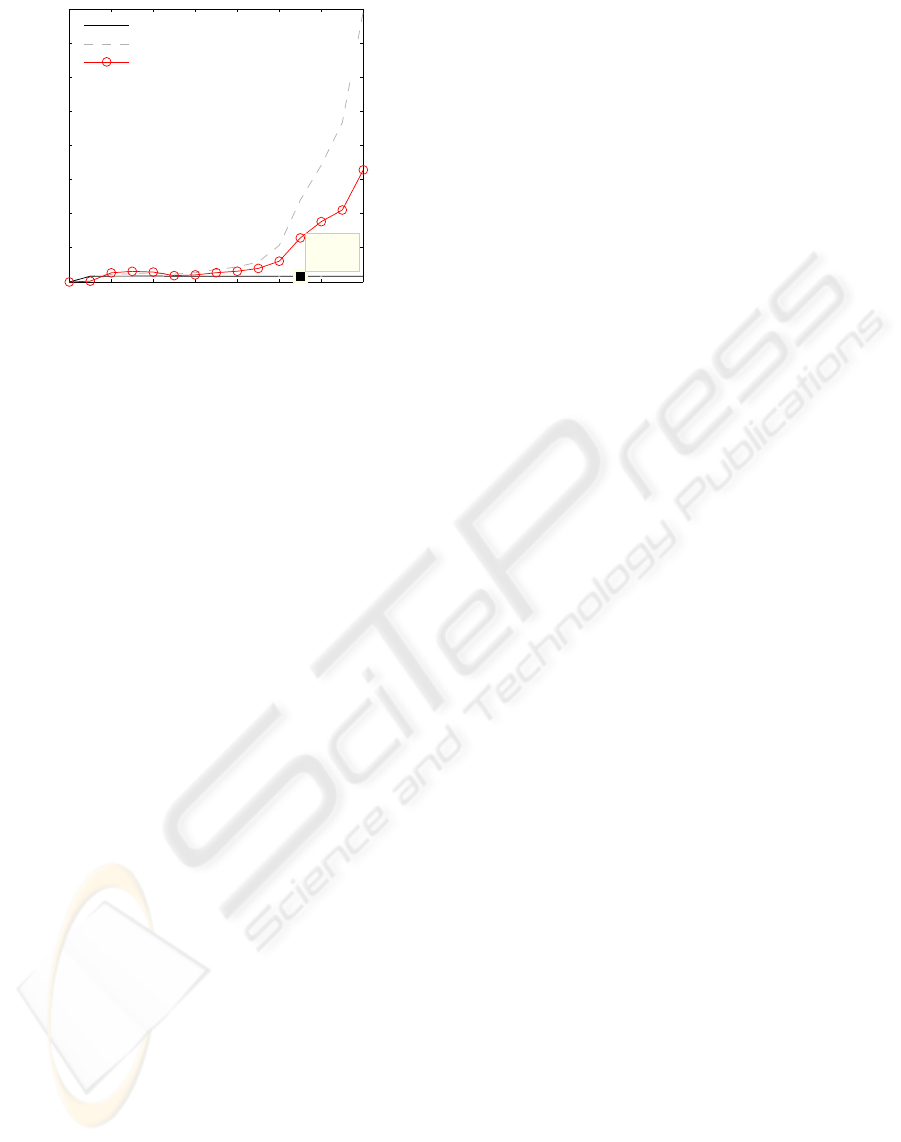
0 20 40 60 80 100 120 140

Mean Error [mm] / No. of iterations

X: 110

Y: 1.685

Registration result (error<=10mm)

Registration result (with errors)

Wrong results (error>10mm)

Figure 2: Inﬂuence of initial misregistration on the mean

error after registration in successful registration cases and

cases where the registration did not decrease the error under

10 mm level. Percentage of these failure cases is shown by

the third series.

could be understood as a mean distance of every point

of a volume to its transformed counterpart.

We continuously generated random transforms, so

that there was at least one hundred of different trans-

forms for each 1 mm level of initial misregistration.

For each misregistration level, the results are the mean

values over all transforms that introduced misregistra-

tion of that level. The graph in Fig. 2 shows two al-

ternative views of the results. First, we ﬁltered only

those results that successfully converged under some

reasonable error (here 10 mm – explained below).

Then the graph also plots values that include all re-

sults. The ﬁgure also shows the statistics of failures,

i.e. the percentage of cases when the method was not

able to decrease under the error level 10 mm. The

failure happens due to the local solution found during

the optimization or due to the maximum number of

iterations reached (the limit was 120 iterations).

The results can be interpreted such that until the

misregistration is up to about 100 mm, the method

converges to the pixel level precision with at least

90% reliability. As misregistration grows over 100

mm (which is approximately the radius of the vol-

ume), the failure rate increases and method’s perfor-

mance decreases mainly due to cases in which method

converged to some false position. We should point out

that these results and trends do not depend on the spe-

ciﬁc value of reasonable error mentioned above. We

use value of 10 mm that is one order higher than the

pixel size and is still reasonable small, but we could

use values 5-45 mm without any signiﬁcant effect on

the graph.

4.2 Inﬂuence of Noise and Rotation Axis

Error on Rotation Estimation

Algorithms for estimation of rotation angle (basic and

improved version described above) were tested for ro-

bustness under non-ideal conditions. First, we want

to examine the inﬂuence of these conditions on algo-

rithm’s behaviour and second, we want to justify the

improvement.

In the ﬁrst part of this experiment, a simulated

MRI brain image (BrainWeb (Collins et al., 1998)

simulated MRI brain image — volume size is 181 ×

217 × 180 with regular 1 mm spacing in all dimen-

sions) was rotated around ﬁxed axis by random an-

gle and Gaussian noise was added to the rotated im-

age. The rotation angle was then recovered by both

basic and improved version of the algorithm and an

absolute difference of estimated and original angle

was measured as an estimation error. We generated

many random angles for each level of noise with a

new instance of noise for each measurement. Graph

3a shows averaged errors over all measurements for

each level of noise.

The second part of this experiment was similar but

instead of adding noise we shifted rotation axis in a

random direction. Hence the algorithms were estimat-

ing rotation around different axis than the image was

originally rotated (note that these algorithms may not

recover original rotation axis). Graph 3b shows de-

pendency of rotation angle error on the distance of

the axis shift (again, error was averaged over many

measurements for each shift distance).

Algorithms proved extreme robustness to noise.

This can be explained due to averaging nature of

PCM: we look for a single peak (ideally delta-

function) in a correlation surface which is result of

an inverse DFT of frequency spectra combined from

the two images. The single peak is kind-of-average

(linear combination) of all frequency samples that are

affected by the same noise as spatial samples of orig-

inal images. The variance of noise is reduced by av-

eraging, hence thanks to large number of samples of

3D volume is the error of estimated rotation angle low

even for really extreme noise.

If the rotation axis is shifted during rotation esti-

mation, the algorithms were able to recover the angle

as long as some structures in the data match. In both

parts of the experiment, it is clearly observable pos-

itive effect of the improvements given in section 3.

The effect of noise is reduced as well as the effect

of disturbances between the two images (shifting the

axis affects mainly the area near rotation axis which

causes most problems in basic version of the algo-

rithm).

3D PHASE CORRELATION USING NON-UNIFORM CYLINDRICAL SAMPLING

257

(a) (b)

−45−40−35−30−25−20

Mean Error [Deg]

SNR

Improved

Basic

0 2 4 6 8 10 12 14

Mean Error [Deg]

Axis shift distance [mm]

Improved

Basic

Figure 3: Inﬂuence of noise (a) and axis error (b) on rotation estimation.

5 CONCLUSIONS

We presented an image registration algorithm that is

able to geometrically align mutually translated and ro-

tated pair of 3D images. The method iteratively re-

covers translational component of misalignment by

PCM and rotational component of misalignment by

applying PCM on cylindrically mapped images. The

improvement was given to the rotation estimation step

to reduce the effect of noise and other image distur-

bances.

The experimental results show that the method is

highly resistant to noise and image disturbances. This

resistance is based on the presented improvement to

the rotation estimation step.

Further improvements would focus on the preci-

sion of the method as the actual CPCM is able to reg-

ister only with the pixel-level precision. We are also

going to examine the multi-modal registration poten-

tial as the correlation of whitened images correlates

mainly the image edges and therefore should be able

to register images with common edges but different

intensity levels.

ACKNOWLEDGEMENTS

The authors would like to thank to Czech Min-

istry of Education for support under the project No.

1M6798555601 (Research Center DAR) and to the

Charles University in Prague for support under the

project GAUK 48908 (Medical Image Registration

and Fusion).

REFERENCES

Baker, M. (1998-2007). www.euclideanspace.com: Maths

- rotations.

Bican, J. and Flusser, J. (2007). Cylindrical phase correla-

tion method. In Kropatsch, W. G., Kampel, M., and

Hanbury, A., editors, Computer Analysis of Images

and Patterns, 12th International Conference, CAIP

2007, Vienna, Austria, August 27-29, 2007, Proceed-

ings, volume 4673 of Lecture Notes in Computer Sci-

ence, pages 751–758. Springer.

Collins, D. L., Zijdenbos, A. P., Kollokian, V., Sled, J. G.,

Kabani, N. J., Holmes, C. J., and Evans, A. C. (1998).

Design and construction of a realistic digital brain

phantom. IEEE Trans Med Imaging, 17(3):463–468.

De Castro, E. and Morandi, C. (1987). Registration of trans-

lated and rotated images using ﬁnite Fourier trans-

form. IEEE Trans. Pattern Analysis and Machine In-

telligence, 9(5):700–703.

Keller, Y., Shkolnisky, Y., and Averbuch, A. (2006). Volume

registration using the 3-D pseudopolar Fourier trans-

form. IEEE Trans. Image Processing, 54(11):4323–

4331.

Kuglin, C. and Hines, D. (1975). The phase correlation

image alignment method. In Proc. Int. Conf. on Cy-

bernetics and Society, pages 163–165. IEEE.

Press, W., Flannery, B., Teukolsky, S., and Vetterling, W.

(1992). Numerical Recipes in C. Cambridge Univer-

sity Press, second edition.

Reddy, B. and Chatterji, B. (1996). An fft-based technique

for translation, rotation, and scale-invariant image reg-

istration. IEEE Trans. Image Processing, 5(8):1266–

1271.

Zitov´a, B. and Flusser, J. (2003). Image registration

methods: a survey. Image and Vision Computing,

21(11):977–1000.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

258