SIGNIFICANCE OF THE WEIBULL DISTRIBUTION AND ITS

SUB-MODELS IN NATURAL IMAGE STATISTICS

Victoria Yanulevskaya and Jan-Mark Geusebroek

Intelligent Systems Lab Amsterdam, Informatics Institute, University of Amsterdam

Kruislaan 403, Amsterdam, The Netherlands

Keywords:

Natural image statistics, Weibull distribution, Model selection.

Abstract:

The contrast statistics of natural images can be adequately characterized by a two-parameter Weibull distribu-

tion. Here we show how distinct regimes of this Weibull distribution lead to various classes of visual content.

These regimes can be determined using model selection techniques from information theory. We experimen-

tally explore the occurrence of the content classes, as related to the global statistics, local statistics, and to

human attended regions. As such, we explicitly link local image statistics and visual content.

1 INTRODUCTION

While looking at the world around us, we see a wide

variety of images. These images, being a visual pro-

jection of the world on our eye, are not random, but

highly organized and structured. This is reﬂected

in the statistics of natural images. With natural im-

ages, we mean real-world photos, including both nat-

ural landscapes and man-made environments. Sur-

prisingly, the contrast statistics of such natural im-

ages can be adequately described by a simple model

(Geusebroek & Smeulders, 2003).

Natural image statistics have widely been studied

in the ﬁeld of image coding (Field, 1987), image com-

pression and image representation (Mallat, 1989), and

more recently, in 3D scene geometry understanding

(Nedovic et al., 2007), visual categorization (Oliva &

Torralba, 2001). Despite its apparent importance, not

many efforts have been undertaken to gain a funda-

mental insight in understanding the cause and signiﬁ-

cance of these statistics.

One of the most important image statistics is the

distribution of contrasts. Mallat (1989) and later Si-

moncelli (1999) propose the generalized Laplacian

distribution as a parameterized model which provides

a good ﬁt to the statistics of natural images. Huang

and Mumford (1999) systematically investigate vari-

ous statistical properties of natural images on a large

calibrated image database (van Hateren, 1998). They

conﬁrm that the statistics involving linear ﬁlters can

be modeled by a generalized Laplacian distribution.

Geusebroek and Smeulders (2005) generalize these

ﬁndings in showing that the dominant distribution of

texture statistics follows the Weibull distribution. An

overview of statistical modelling of natural images

can be found in Srivastava et al. (2003).

Scholte et al. (2008) examined to which degree

the brain is sensitive to these natural image statistics,

by considering the ERP brain measurements of hu-

man subjects. They found a correlation of 84% and

93% between the Weibull parameters as derived from

images and a simple model of ERP measurements

obtained from the parvo- and magnocellular system.

Given these results, one would expect the Weibull dis-

tribution to play a signiﬁcant role in image statistics.

The central question we address in this paper is:

In how far can natural image statistics explain visual

content? To address this question, we explore edge

distributions of natural images at the global and local

level. We distinguish four classes of natural images

according to the behavior of the Weibull distribution.

As we will show, each class seems to reﬂect a speciﬁc

type of visual content. Furthermore, we study the oc-

currence of the different classes for human attended

regions.

Novel in our approach is the explicit link between

regional statistics and visual content, as reﬂected in

the Weibull sub-models. Furthermore, from a human

attention perspective we study the importance of each

sub-model.

The paper is organized as follows. Section 2 in-

troduces the integrated Weibull distribution to cap-

ture the natural image statistics. The maximum like-

lihood estimators of the Weibull parameters are pro-

355

Yanulevskaya V. and Geusebroek J. (2009).

SIGNIFICANCE OF THE WEIBULL DISTRIBUTION AND ITS SUB-MODELS IN NATURAL IMAGE STATISTICS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 355-362

DOI: 10.5220/0001793203550362

 SciTePress

vided. Furthermore, we distinguish four different sub-

models of the Weibull distribution, and apply infor-

mation theory to differentiate these sub-models. We

present the g-test as a goodness of ﬁt test between the

data and the Weibull distribution. In Section 3 we

explore the occurrence of the different sub-models of

the Weibull distribution on an image data set, and we

link the sub-models to the visual content. We consider

three experiments. We start by analyzing the statistics

of the whole image. Then we zoom in on the local

image statistics. Finally, we explore the statistics of

human attended regions. We wrap up with conclu-

sions in Section 4.

2 IMAGE STATISTICS

The parameterized model which provides a good ﬁt

to the edge distribution of natural images (Geuse-

broek & Smeulders, 2003; Simoncelli, 1999; Huang

& Mumford, 1999) has a probability density function

(pdf) given by,

p(x) =

2γ

βΓ(

)

exp



−





, (1)

where x is the edge response to the Gaussian deriva-

tive ﬁlter, γ > 0 is the shape parameter and β > 0 is the

scale parameter of the distribution. Γ(·) is the com-

plete Gamma function,

Γ(x) =

∞

x−1

exp

−t

dt. (2)

Through out the paper we will refer to this model

as the two parameter integrated Weibull distribution,

considering its close relationship to the Weibull dis-

tribution (Geusebroek & Smeulders, 2003). The pa-

rameter β denotes the width of the distribution and

the parameter γ represents the peakness of the distri-

bution. The width β reﬂects the local contrast. A wide

distribution indicates a texture with high contrast. The

shape γ is sensitive to the local edge spatial frequency.

These two parameters catch the structure of the image

texture (Geusebroek & Smeulders, 2005). Figure 1 il-

lustrates the integrated Weibull pdf for some example

images.

The integrated Weibull distribution captures the

behavior of other statistical distributions, mainly be-

ing the power-law, exponential, and gaussian distri-

bution. Our aim is to explore the link between the

Weibull statistics and visual content. Hence, besides

investigating the variation in image content as func-

tion of the Weibull parameters by means of scatter

plots, we will explore visual content by categorizing

these statistical sub-models. To distinguish between

Figure 1: Integrated Weibull PDF’s for different kind of tex-

tures: object-background image (a), images with moderate

contrast content (b), high-frequency texture image (c) and

image with a regular pattern (d).

the different sub-models, we need to know parame-

ters of each model. They can be estimated with the

Maximum Likelihood Estimation (MLE) technique.

After that, we can quantify the various sub distribu-

tions using model selection techniques.

2.1 Maximum Likelihood Estimation

The likelihood function indicates how well a distri-

bution describes the observed data X = x

,...,x

The best ﬁt is obtained when model parameters max-

imize the log-likelihood function, in which case their

respective derivatives should equal zero. For the in-

tegrated Weibull distribution given by Eq.(1), the best

ﬁt is obtained when

∂

∂β

lnL

(β,γ|X) = −

∑

i=1



= 0, (3)

and

∂

∂γ

lnL

(β,γ|X) =



γ − 1 + ψ





+ln(γ) +

∑

i=1



−

∑

i=1



= 0, (4)

where,

ψ(γ) =

dγ

lnΓ(γ) =

dγ

Γ(γ)

(5)

is the digamma function.

The parameter γ is obtained by eliminating β from

Eq. (4):

f (γ,X) = −

∑

i=1

∑

i=1

∑

i=1

1 +

ln(γ) +





= 0. (6)

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

356

Eq. (6) may be solved using standard iterative pro-

cedures, for example, the Newton-Raphson method:

k+1

= γ

−

f (γ

)

∂

∂γ

f (γ

)

∂

∂γ

f (γ,X) =

∑

i=1

∑

i=1

− n

∑

Λ −

− n

∑

i=1

Λln



∑

i=1



, (7)

where

Λ =

∂

∂γ



∑

i=1



. (8)

The Newton-Raphson algorithm works as shown

in Alg. 1. Thus, the maximum likelihood estimator

is the solution of Eq. (6) and then

β can be calculated

from Eq. (3), until convergence.

Algorithm 1 Integrated Weibull parameter estima-

tion.

γ = 1 initial value

ε = 0.001 accuracy of the calculations

= γ −

f (γ,X)

∂

∂γ

f (γ,X)

while |γ

− γ| > ε

γ = γ

= γ −

f (γ,X)

∂

∂γ

f (γ,X)

return γ

MLE for parameters of the power law, the expo-

nential, and the Gaussian distribution are well known

and can be easily calculated. Their pdf’s are given by

P(x) =



β−1

, (9)

E(x) =

2β

exp



−





, (10)

G(x) =

2πβ

exp



−

2β



. (11)

The corresponding maximum likelihood estima-

tions are

−

∑

i=1

log(|

, (12)

∑

i=1

, (13)

∑

i=1

)

. (14)

2.2 Model Selection

We use Akaike’s information criterion (AIC) (Akaike,

1973) for appropriate model selection. AIC estimates

expected Kullback-Leibler information, based on the

log-likelihood function at its maximum point. Hence,

we do not need to assume that the ”true model” is in

the set of candidates (Burnham & Anderson, 2004).

AIC for model i is

AIC

= −log(L

(

|X))+ K

, (15)

where L

is the likelihood function of the model i,

is the maximum likelihood estimator of the model pa-

rameters based on the assumed model i and the data

X, and K

is the number of parameters of the model

i. In our case, parameter

is deﬁned by Eq. (12)-

(14) for each particular model. In the end we have

three AIC values corresponding to the power law, the

exponential, and the Gaussian distribution. The best

model is the one with minimum value AIC

min

. How-

ever, we follow (Burnham & Anderson, 2002) and as-

sign a probability to each model by

exp(−∆

/2)

r=1

exp(−∆

/2)

, (16)

where

∆

= AIC

− AIC

min

(17)

and R is the number of models, R = 3 in our case. The

are called Akaike weights and are interpreted as a

probability that model i ﬁts the data X best over the

considered set of models.

2.3 g-Test

Sometimes none of the considered models represents

the data appropriately. Thus, it should be tested how

well the integrated Weibull distribution ﬁts the data.

The g-test is the log-likelihood equivalent of the chi-

squared test, given by:

g = 2

∑

j=1

log





, (18)

where O

is the number of observed values x

in bin

j of the histogram of the data X. Furthermore, E

a number of expected values in the same bin j under

the ﬁtted distribution. The hypothesis that the distri-

bution is of a given form is accepted if the calculated

test statistic g is less than an appropriate critical value.

The g-test can be applied with the same critical values

as the chi-squared test. In this paper we use a criti-

cal value which corresponds to a signiﬁcance level of

α = 0.05 and 100 degrees of freedom (g < 77.929)

(Filliben, 2002).

SIGNIFICANCE OF THE WEIBULL DISTRIBUTION AND ITS SUB-MODELS IN NATURAL IMAGE STATISTICS

357

2.4 The Four Regimes of the Integrated

Weibull Distribution

We can now distinguish four types of natural images

according to the behavior of the integrated Weibull

distribution. When the integrated Weibull distribution

ﬁts the data well, its sub-models deﬁne the ﬁrst three

types, being: the power law, the exponential or the

Gaussian. The fourth type of natural images occurs

when the integrated Weibull distribution does not de-

scribe the data well. Our aim is to assign one particu-

lar type to a (sub-)image.

3 EXPERIMENTS

To illustrate the different regimes of the integrated

Weibull distribution, we analyze a data set contain-

ing 107 natural images of size 800x540 pixels. These

images are selected from three categories of National

Geographic wallpapers

: animals, landscapes, and

people. We are interested in the intensity edge dis-

tribution and its sub-models according to the four

regimes of the integrated Weibull distribution. To ob-

tain the intensity edge distribution, we do not use the

standard edge ﬁlters, e.g. Sobel style, instead we ap-

ply the Gaussian derivative ﬁlter (σ = 1) and steer

it in the gradient direction. Then we consider a his-

togram (101 bins) of the responses, and ﬁt the inte-

grated Weibull distribution to this histogram. Finally,

we select the appropriate sub-model using Akaike’s

information criterion.

3.1 Global Image Statistic Analysis

We start by analyzing the presence of the various in-

tegrated Weibull sub-models in the statistics of the

whole image. We extract edges and study their dis-

tribution globally for each image from the data set.

The results are shown in Table 1.

Table 1: Four regimes of the integrated Weibull distribution

for global image analysis.

Int. Weibull Not Int. Weibull

100% 0%

Power Law Exp. Gauss. -

20% 78% 2% -

All images ﬁt well to the integrated Weibull distri-

bution according to the g-test (α = 0.05). Power law

distribution is chosen as an appropriate sub-model for

http://www.nationalgeographic.com/

20% of the images. These images have well separated

foreground and uniform background regions, see Fig-

ure 2(a). Only 2% of the images are Gaussian dis-

tributed, these are images which contain mostly high-

frequency texture, illustrated in Figure 2(c). Most of

the images (78%) follow the exponential distribution,

which refers to moderate contrast contents. These im-

ages usually contain a lot of details at different scales,

see Figure 2(b).

Figure 3 gives an overview of the occurrence of

each sub-model in the entire image collection. Each

of the sub-models indicates different image content.

Images with strong object-background contrasts are

close to the power law behavior. Images with mod-

erate contrast tend to follow the exponential distribu-

tion. High-frequency texture images are described by

the Gaussian distribution.

(a)

(b) (c)

Figure 2: Typical images for three sub-models of the inte-

grated Weibull distribution. Figure (a) corresponds to the

power law sub-model, (b) and (c) show, respectively, exam-

ples for the exponential and the Gaussian sub-models.

3.2 Local Image Statistic Analysis

Edge distributions of natural images follow the in-

tegrated Weibull when looking at global statistics

as shown above. More important, the various sub-

models of the integrated Weibull distribution seem to

reﬂect visual content. One would expect this effect

to be even stronger when considering local patches,

as local visual content is more coherent. Therefore,

for the local analysis, we divide images into rectan-

gular patches (60x60 pixels) and consider the edge

histogram and model selection over these patches.

Results are presented in Table 2. For experimen-

tal setup reasons (see below), we consider a subset

of 49 images, however, results for the whole data set

are similar (data not shown). Comparing these re-

sults with the global analysis (Table 1), local patches

do not always follow the integrated Weibull distribu-

tion according to the g-test (α = 0.05). For one, re-

gions without edges are dominated by compression

artifacts and may not follow the integrated Weibull

distribution. Furthermore, in many cases, patches are

composed of a few parts, each following a different

sub-model. Thus, each part seems to conform the

integrated Weibull distribution, but all together they

do not follow one of the sub-models. In the global

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

358

Figure 3: Scatter plot of integrated Weibull parameters β

and γ with each image positioned at its respective (β,γ) val-

ues. The horizontal axis represents the value of the β param-

eter, indicating contrast. The vertical axis represents value

of the γ parameter (between 0 and 3). A red frame indicates

the image is ﬁtted by the power law distribution. Images

with blue frames follow the exponential distribution. Yel-

low framed images are described with the Gaussian distri-

bution.

analysis, we have the same situation, where images

are composed of many parts due to objects and clut-

ter. However, the resulting distribution of the whole

image combines into the exponential distribution due

to the large amount of parts (Burghouts et al., 2007).

This explains the smaller portion of local patches de-

scribed with the exponential sub-model in compari-

son with the global analysis.

Table 2: Four regimes of the integrated Weibull distribution

for local region analysis.

Int. Weibull Not int. Weibull

87% 13%

Power Law Exp. Gauss. -

26% 47% 14% -

The Gaussian sub-model occurs more often at lo-

cal scale. The Gaussian distribution describes uni-

form regions of high-frequency textures. Images con-

taining only high-frequency textures are rather rare in

a photo stock. However, uniform textured regions do

occur in images, and local analysis reﬂects this. Com-

paring the results for the power law sub-model, the

model behaves relatively similar at the global and lo-

cal levels.

Figure 4 illustrates how the patch’s visual content

is reﬂected by the integrated Weibull sub-models. The

ﬁgure represents a scatter plot of integrated Weibull

parameters β and γ with each patch positioned at its

respective (β,γ) value. The power law sub-model

is concentrated at the bottom which corresponds to

small γ values (γ < 1). This sub-model is linked to

the patches containing uniform regions separated by

strong edges, but are not very detailed, as shown in

the inset. The exponential sub-model spans a wide

range of γ values, starting within the power law sub-

model, and ending at the lower regions of the Gaus-

sian sub-model. This sub-model corresponds to γ val-

ues around 1 and describes more detailed patches.

The Gaussian sub-model ends up at the top of the

ﬁgure, where the γ parameter is close to 2. High-

frequency with high contrast patches are reﬂected in

the Gaussian sub-model, as well as smoothed patches

with Gaussian noise.

3.3 Attention based Analysis of Local

Image Statistics

Visual content is closely connected to human atten-

tion while observing the world around us. Our vi-

sual system samples the environment not randomly,

but is driven by visual stimuli, like variations in con-

trast or color (Baddeley & Tatler, 2006; Itti et al.,

1998; Mante et al., 2005; Reinagel & Zador, 1999).

We are interested in the occurrence of various sub-

models of the integrated Weibull distribution in the

statistics of local regions attended by humans. To

obtain the ground truth attended regions, human eye

ﬁxations were recorded for the subset of 49 images.

Eighteen subjects participated in the experiment, they

were shown each image for 5 seconds. For each ﬁx-

ation point we consider a fovea-sized patch (60x60

pixels). Again the local edge distribution analysis is

applied for each ﬁxated patch.

Based on the results shown in Table 3, we can con-

clude that attended regions differ from arbitrary se-

lected local regions (Table 2). People tend to look to

strong edges, which are power law distributed, in our

results 33% for attended regions compared to 26% for

arbitrary regions, respectively.

Gaussian distributed patches occur more rare in at-

tended regions in comparison with arbitrary regions,

7% versus 14%. The examples of Gaussian regions in

Figure 4 (in yellow frames) show two types of Gaus-

sian distributed patches. As one can notice, smooth

patches with gaussian-like noise on the top left are

not informative, thus, people generally do not ﬁxate

on such kind of regions. Instead, people look to de-

SIGNIFICANCE OF THE WEIBULL DISTRIBUTION AND ITS SUB-MODELS IN NATURAL IMAGE STATISTICS

359

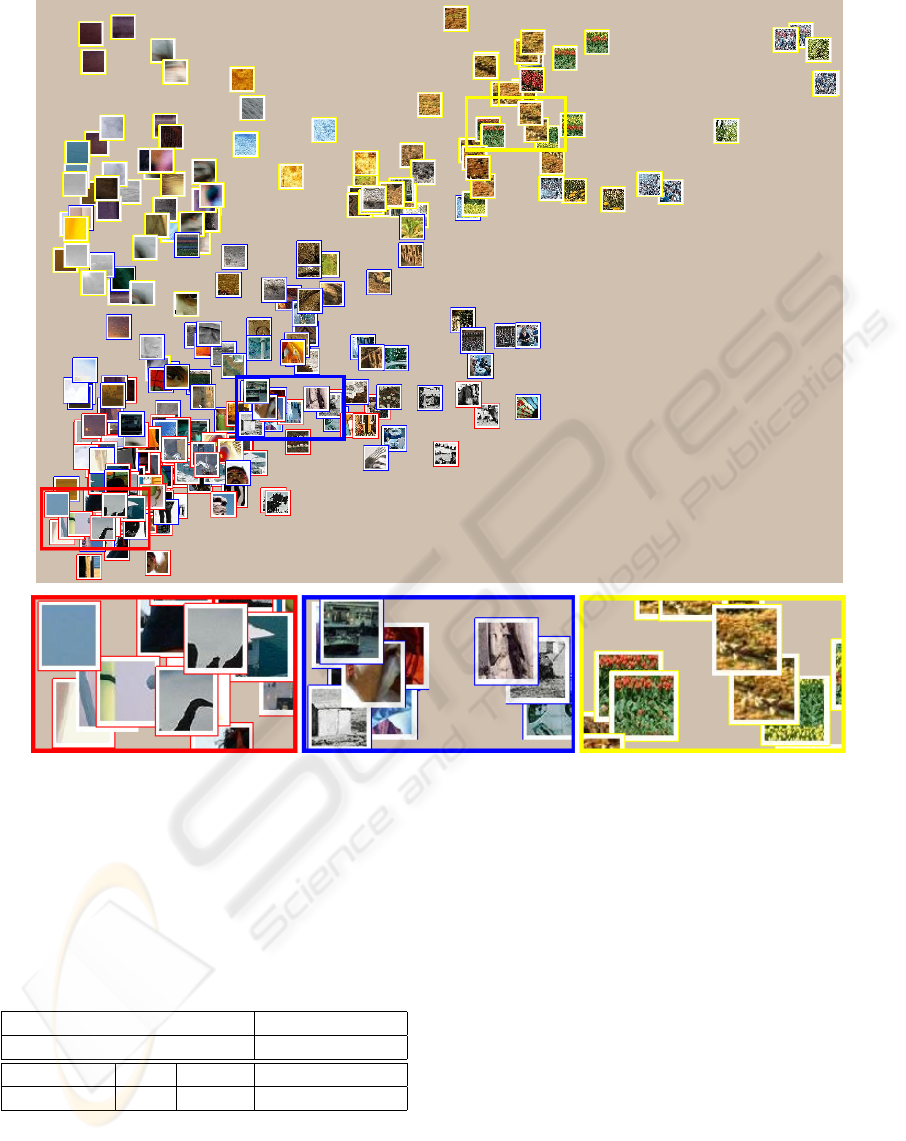
Figure 4: Scatter plot of integrated Weibull parameters β and γ with each patch positioned at its respective (β,γ) value. Again,

the horizontal axis represents value of the β parameter, and the vertical axis represents value of the γ parameter (between

0 and 3). Red framed patches correspond to the power law sub-model. These patches contain uniform regions separated

by strong edges, but are not very detailed, see the inset on the bottom left. Patches with blue frames follow the exponential

distribution. Clearly they are showing more small scale details, as illustrated by the inset in the middle. Yellow framed patches

are Gaussian distributed, there we observe two types of visual content. On the top right, high-frequency with high contrast

patches are gathered, enlarged version is in the bottom right inset. On the top left, there are smooth patches with gaussian-like

noise.

Table 3: Four regimes of the integrated Weibull distribution

for attended region analysis.

Int. Weibull Not int. Weibull

95% 5%

Power Law Exp. Gauss. -

33% 55% 7% -

tailed regions, which follow the exponential distribu-

tion. In our attention based analysis, the exponential

sub-model is present in 55% of the results (Table 3),

whereas this is only for 47% the case when consid-

ering arbitrary regions (Table 2). Regions which do

not follow the integrated Weibull distribution accord-

ing to the g-test, are less present in attended regions

than in arbitrary regions, 5% versus 13%. This is may

be due to the portion of regions without edge content

as discussed previously.

Figure 5 illustrates the occurrence of different

regimes of the integrated Weibull distribution with su-

perimposed human gaze directions. As can be seen

from the Figure, subjects seldom look to the Gaus-

sian distributed regions, but prefer areas which follow

the power law and the exponential distributions.

As discussed in Section 2, the integrated Weibull

parameter β reﬂects the local contrast. From literature

it is known that contrast plays an important role in

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

360

Figure 5: Visualization of the integrated Weibull sub-

models with superposed human gaze directions. On the

left two example images. On the right a visualization

of the local model selection and the eye-tracking experi-

ment. The black areas correspond to patches with power

law sub-model, dark and light grey areas correspond to

patches with the exponential and Gaussian sub-models, re-

spectively. White small squares depict the human ﬁxation

points.

human eye ﬁxations (Reinagel & Zador, 1999; Bad-

deley & Tatler, 2006). Table 3 illustrates the mean

values of the parameter β within each sub-model for

arbitrary regions versus attended regions. The t-test

shows that the local contrast captured by β is signif-

icantly higher (p < 10

−10

for each sub-model) in av-

erage for attended regions than for arbitrary regions.

Therefore, our experiments reproduce the tendency of

people to look at higher contrast regions. The results

identify both contrast and edge frequency reﬂected in

the integrated Weibull parameters and its sub-models

might be cues for human attention.

Table 4: Mean integrated Weibull β parameter.

Power Law Exp. Gauss.

Arbitrary regions 0.0090 0.0149 0.0249

Attended regions 0.0119 0.0189 0.0287

4 CONCLUSIONS

In this paper, we have explored the link between vi-

sual content and natural image statistics modelled by

the integrated Weibull distribution. We have given

four different regimes with respect to the integrated

Weibull distribution: power-law, exponential, Gaus-

sian, and the case when the integrated Weibull distri-

bution is not appropriate. With model selection tech-

niques from information theory, we can determine the

probability for every sub-model to explain the statis-

tical properties of the regions. Our results show that

natural image statistics explain a lot of visual content.

Each sub-model reﬂects a speciﬁc type of visual con-

tent, at the global (see Figure 3), and at the local level

(see Figure 4).

At the global level, all images from our collection

follow the integrated Weibull distribution, see Table 1.

Most of the images, around 80%, are exponentially

distributed. The rest is mainly power law distributed,

the Gaussian distribution being rare. In the local anal-

ysis we have considered the statistics of arbitrary and

attended regions, see Tables 2 and 3, respectively. We

have shown that the occurrence of the various sub-

models in human attended versus arbitrary regions is

signiﬁcantly different. This might indicate a role of

the Weibull sub-models in human attention.

In future work, we plan to address salient re-

gion detection algorithms based on these local image

statistics. Furthermore, recent studies show natural

image statistics play an important role in 3D scene

perception (Pelli & Tillman, 2008). We plan to further

exploit the various Weibull sub-models in condensed

representations of 3D scenes.

REFERENCES

Akaike, H. (1973). Information Theory and an Extension

of the Maximum Likelihood Principle. Int. Sympos.

Inform. Theory (pp. 267–281).

Baddeley, R. J. & Tatler, B. W. (2006). High frequency

edges (but not contrast) predict where we ﬁxate: A

Bayesian system identiﬁcation analysis. Vision Res.,

46(18), 2824–2833.

Burghouts, G. J., Smeulders, A. W. M. & Geusebroek, J. M.

(2007). The distribution family of similarity distances.

In NIPS.

Burnham, K. P. & Anderson, D. R. (2002). Model selection

and multimodel inference: A Practical Information-

Theoretic Approach. Springer.

Burnham, K. P. & Anderson, D. R. (2004). Multimodel In-

ference: Understanding AIC and BIC in Model Selec-

tion. Sociological Methods & Research, 33(2), 261.

Field, D. J. (1987). Relations between the statistics of natu-

ral images and the response properties of cortical cells.

J. Opt. Soc. Am., 4, 2370–2393.

Filliben, J. J. (2002). NIST/SEMATECH

e-Handbook of Statistical Methods.

http://www.itl.nist.gov/div898/handbook/. NIST,

Gaithersburg.

Geusebroek, J. M. & Smeulders, A. W. M. (2003). Frag-

mentation in the vision of scenes. In ICCV.

SIGNIFICANCE OF THE WEIBULL DISTRIBUTION AND ITS SUB-MODELS IN NATURAL IMAGE STATISTICS

361

Geusebroek, J. M. & Smeulders, A. W. M. (2005). A six-

stimulus theory for stochastic texture. Int. J. Comput.

Vision, 62(1), 7–16.

van Hateren, J. H. (1998). Independent component ﬁlters of

natural images compared with simple cells in primary

visual cortex. Biological Sciences, 265(1394), 359–

366.

Huang, J. & Mumford, D. (1999). Statistics of natural im-

ages and models.

Itti, L., Koch, C. & Niebur, E. (1998). A model of saliency-

based visual attention for rapid scene analysis. Trans.

Pattern Anal. Machine Intell., 20(11), 1254–1259.

Mallat, S. G. (1989). A theory for multiresolution signal

decomposition: the wavelet representation. Pattern

Anal. Machine Intell., 11(7), 674–693.

Mante, V., Frazor, R. A., Bonin, V., Geisler, W. S. & Caran-

dini, M. (2005). Independence of luminance and con-

trast in natural scenes and in the early visual system.

Nature Neurosci., 8(12), 1690–7.

Nedovic, V., Smeulders, A. W. M., Redert, A. & Geuse-

broek, J. M. (2007). Depth information by stage clas-

siﬁcation. In ICCV.

Oliva, A. & Torralba, A. (2001). Modeling the shape of

the scene: A holistic representation of the spatial en-

velope. Int. J. Comput. Vision, 42(3), 145–175.

Pelli, D. G. & Tillman, K. A. (2008). The uncrowded win-

dow of object recognition. Nature Neurosc. (p. to ap-

pear in october).

Reinagel, P. & Zador, A. (1999). Natural scene statistics at

the centre of gaze. Network: Comput. Neural Syst.,

10(4), 341–350.

Scholte, H. S., Ghebreab, S., Smeulders, A. W. M. &

Lamme, V. (2008). The parvo and magno-cellular sys-

tems encode natural image statistics parameters. J. Vi-

sion, 8(6), 686a.

Simoncelli, E. P. (1999). Modeling the joint statistics of

images in the wavelet domain. Volume 3813 (pp. 188–

195).

Srivastava, A., Lee, A. B., Simoncelli, E. P. & Zhu, S. C.

(2003). On Advances in Statistical Modeling of Nat-

ural Images. J. Math. Imaging Vision, 18(1), 17–33.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

362