A REVIEW ON THE CURRENT SEGMENTATION

ALGORITHMS FOR MEDICAL IMAGES

Zhen Ma, João Manuel R. S. Tavares and R. M. Natal Jorge

Faculty of Engineering, University of Porto, Porto, Portugal

Keywords: Medical Image Segmentation, Algorithm Review, Pelvic Cavity.

Abstract: This paper makes a review on the current segmentation algorithms used for medical images. Algorithms are

divided into three categories according to their main ideas: the ones based on threshold, the ones based on

pattern recognition techniques and the ones based on deformable models. The main tendency of each

category with their principle ideas, application field, advantages and disadvantages are discussed. For each

considered type some typical algorithms are described. Algorithms of the third category are mainly focused

because of the intensive investigation on deformable models in the recent years. Possible applications of

these algorithms on segmenting organs and tissues contained in the pelvic cavity are also discussed through

several preliminary experiments.

1 INTRODUCTION

The developments of imaging techniques such as

Computer Tomography (CT) and Magnetic

Resonance Imaging (MRI) offer doctors with high

resolution images which have greatly assisted the

clinical diagnosis. Meanwhile medical technicians

have to process a large number of images with much

more details; Segmentation is usually a necessary

step for the task. However, manual segmentation is

very time-consuming and the results may not be

reproducible or suffer from intra-observer and inter-

observer variability. Compared with the algorithms

for common image processing, the ones used for

medical images require more concrete application

background. Priori knowledge like the imaging

procedure and the biomechanical behaviours of

organs or structures can be critical for a successful

segmentation. Also, medical images are usually

influenced by noises and partial volume effect (Zaidi,

2005), algorithms should be sophisticated enough to

handle the segmentation task. In the past few

decades, many effective algorithms have been

proposed to perform the computer-aided

segmentation. The successful implementations of

modern mathematical and physical techniques have

considerably enhanced the accuracy of the

segmentation. In the following sections, these

algorithms are classified into three categories:

algorithms based on threshold, algorithms based on

pattern recognition techniques and algorithms based

on deformable models. We focus on the main ideas

of each category and summarize their trend and

possible applications. In the end, the features of each

type are illustrated with an example of their possible

applications to segment the pelvic cavity. We also

point out that since most of the algorithms

incorporate multiple techniques, the classification of

an algorithm may not be definite.

The paper is organized as follows: In the next

section, we make a review of the algorithms; In

Section 3, we summarize the advantages and

disadvantages of each category and discuss their

possible applications to the pelvic cavity; In Section

4, we give the conclusion.

2 ALGORITHMS REVIEW

2.1 Algorithms Based on Threshold

Most of the algorithms that belong to this category

make the premise that the interested structures can

be discerned by quantifiable features, like image

intensity or gradient magnitude. Segmentation is a

procedure of searching for pixels that satisfy the

rules defined by the thresholds. Thresholds in these

algorithms can be selected manually according to

priori knowledge or automatically through image

135

Ma Z., R. S. Tavares J. and Natal Jorge R. (2009).

A REVIEW ON THE CURRENT SEGMENTATION ALGORITHMS FOR MEDICAL IMAGES.

In Proceedings of the First International Conference on Computer Imaging Theory and Applications, pages 135-140

DOI: 10.5220/0001793501350140

 SciTePress

information. Algorithms can be further divided to

edge-based ones, region-based ones and hybrid ones.

Thresholds in the edge-based algorithms are

related with the edge information. Structures are

depicted by edge points. Common edge detection

algorithms such as Canny edge detector (Canny,

1986) and Laplacian edge detector can be classified

to this type. Algorithms try to find edge pixels while

eliminate the noise influence. For example, Canny

edge detector uses the threshold of gradient

magnitude to find the potential edge pixels and

suppresses them through the procedures of the non-

maximal suppression and hysteresis thresholding. As

the operations of algorithms are based on pixels, the

detected edges are consisted of discrete pixels

therefore may be incomplete or discontinuous.

Hence, it is necessary to apply post-processing like

morphological operation to connect the breaks or

eliminate the holes.

The ideas of region-based algorithms come from

the observation that pixels inside a structure tend to

have similar intensities. Region growing algorithm

(Adams and Bischof, 1994) is a typical algorithm of

this type. After selecting initial seeds, algorithms

begin to search for the neighboured pixels whose

intensities are inside the intervals defined by the

thresholds and then merge them to expand the

regions. To eliminate the dependence on initial seeds

and make the algorithm automatically, statistical

information and priori knowledge can be

incorporated to the algorithms. For example, a

homogeneity criterion was introduced in (Pohle and

Toennies, 2001)

which made the region growing

algorithms adaptive for the different locations of

initial seeds and achieved success in the

segmentation of CT and MR images. However, as

the algorithms mainly rely on the image intensity

information, they are hard to handle the partial

volume effects and control the leakage.

Information used in the hybrid algorithms

combine different image cues to complete the

segmentation. Typical examples are the watershed

algorithms (Beucher and Lantuéjoul, 1979) which

combine the image intensity with the gradient

information. In the watershed algorithms, gray scale

images are considered as reliefs and the gradient

magnitude of each pixel is treated as elevation.

Watershed lines are defined to be the pixels with

local maximum of gradient magnitude. The

segmentation procedure is to construct watersheds

during the successive flooding of the gray value

relief. Due to the combination of image information,

watershed algorithms can achieve better results, but

these algorithms tend to over-segmentation

especially when the images are noisy or the objects

themselves have low signal-to-noise ratio. Hybrid

threshold-based algorithms can further combine with

other techniques to perform the segmentation (Ng, et

al, 2006).

Due to the noise influence and partial volume

effect, the edges of organs or structures in medical

images are usually not clearly defined therefore

algorithms based on threshold are seldom used alone.

2.2 Algorithms based on Pattern

Recognition Techniques

As structures in medical images can be treated as

patterns, techniques from pattern recognition fields

can be used to perform the segmentation.

Classification algorithms are the most popular ones

for the medical image segmentation. In the

following, we mainly review the supervised

classification algorithms and the unsupervised ones.

Popular techniques used by the supervised

algorithms include supervised artificial neural

network (Alirezaie, et al, 1997), support vector

machine (Wang, et al 2001) and active appearance

models (Cootes, et al, 2001). A training set is needed

to get the classifiers. Supervised artificial neural

networks (ANNs) and support vector machines

(SVMs) are non-linear statistical data modeling tools

and can be used to model complex relationships

between inputs and outputs. Weights in the classifier

are selected through optimizing energy functionals

defined by the features of structures and are updated

through processing each sample in the training set.

The extracted information from the training set

provides important cues of the structures such as

intensity, position and shape, which can be valuable

complementary information for the segmentation of

test images. Active appearance models (AAM) are

statistical models of the shape of structures. Training

samples are used to extract the mean shape, mean

appearance and define ranges of shape parameters.

Restrictions on shape parameters guarantee the

similarity between the segmentation result and the

training samples. The segmentation procedure is to

find the better positions of the shape points

according to the appearance information. Algorithms

based on classifiers have been widely applied to

segment organs in medical images like cardiac and

brain images. If properly modelled, supervised

classification algorithms can greatly enhance the

segmentation accuracy. However, supervised

classification algorithms are sensitive to the initial

conditions. To guarantee the correctness of the

results, the training set must contain enough samples

IMAGAPP 2009 - International Conference on Imaging Theory and Applications

136

and the samples should be representative and

segmented accurately.

Popular unsupervised classification algorithms

include Fuzzy C-means algorithm (Mohamed, et al,

1998), Iterative Self-organizing Data Analysis

Technique Algorithm (Wong, et al, 2002) and

unsupervised neural network (Cheng, et al, 1996).

Unsupervised classification algorithms are also

called clustering algorithms. No training set is

needed. Instead, the structure features are extracted

from the classified points. FCM algorithm comes

from C-means (CM) or K-means algorithms, where

C or K is the pre-defined number of clusters. FCM

algorithm is an iterative algorithm with the objective

to minimize the intra-cluster variation. The labelled

pixels are assigned to the nearest clusters basing on

their weighted distances to the cluster centroids, then

the cluster centroid is updated and the pixels are re-

assigned. The algorithm ends when all the pixels

have fixed labels. FCM algorithm is commonly used

for nuclear medicine and transmission image

segmentation (Mohamed, et al, 1998). Iterative Self-

organizing Data Analysis Technique Algorithm

(ISODATA) is similar to the FCM algorithm. The

main difference is ISODATA algorithm allows for

different number of clusters while the FCM assumes

that the number of clusters is known as a priori. In

medical imaging for example the positron emission

tomography (PET) scans, clustering algorithms can

be used to segment different types of tissues and

blood (Wong, et al, 2002). Unsupervised neural

networks are based on unsupervised learning, which

means the targets are the same as the inputs. The

training of weights used in classifiers is based on the

learning rule. For example the Hopfields neural

network adopts the learning rule as winner-takes-all

to simplify the selection of weights. A successful

application of Hopfields neural network to segment

the MR brain images can be seen in (Cheng, et al,

1996). Template matching algorithms and atlas-

guided algorithms which combine the prior

knowledge to asssit the segmentation are also

popular for medical image segmentation (Gindi, et al,

1993; Akselrod-Ballin, et al, 2006).

2.3 Algorithms based on Deformable

Models

Compared with the algorithms of the above two

categories, the ones based on deformable models are

more flexible and can be used for complex

segmentations. According to the representation way

of the contour, deformable models can be classified

to parametric models and geometric models. A

moving equation should be defined to drive the

initial contours to the structure boundaries.

Therefore, the procedure of these algorithms can be

viewed as a modelling of curve evolution.

The parametric deformable models have tight

relationship with the snake method (Kass, et al,

1987). Contours are sampled as discrete points and

are tracked according to their respective moving

equations. The explicit tracking has the advantage of

high computational efficiency therefore allows for

real-time applications. The moving equation for the

parametric deformable models can be derived

through either energy functional or dynamic forces.

The definition of energy functional contains two

parts: internal energy and external energy. The

internal energy aims to keep the smoothness and

regularity of the contour and is usually defined

through the geometric properties of the contour such

as length, area and curvature; the external energy

aims to drive the contour to the right position and

the definition is based on image information. Using

calculus of variations, we can derive an Euler-

Lagrange equation of the energy functional which

states that the balancing equilibrium of the moving

contour under the external forces and the internal

forces is the position of structure boundary. Through

adding the time variable to the Euler-Lagrange

equation, we then get the dynamic moving equation.

Priori knowledge can be easily incorporated to the

procedures of parametric models. Snake method is

the first deformable model applied to the medical

image segmentation. The traditional snake method

relies on the gradient information therefore is

sensitive to the initial position of the contour. The

contour must be placed to the positions near to the

structure boundary so that the external forces are

strong enough to attract the contour. Otherwise the

contours may shrink or stop at wrong positions. The

later proposed algorithms (Cohen, 1991; McInerney

and Terzopoulos, 1995; Xu and Prince, 1998) tried

to eliminate the dependence on the initial conditions

and noise influence. Cohen (Cohen, 1991) added a

balloon force to the external forces to make the

contour inflation or deflation even if the gradient

field is weak. Xu and Prince (Xu and Prince, 1998)

replaced the gradient field with the gradient vector

field (GVF) which achieves the same capture effect

near the structure boundary while changes slowly in

other regions.

The geometric deformable models are based on

the level set method (Osher and Sethian, 1988)

which was initially proposed to handle the

topological changes during the curve evolution. The

main idea of the level set method is to implicitly

A REVIEW ON THE CURRENT SEGMENTATION ALGORITHMS FOR MEDICAL IMAGES

137

embed the moving contour into a higher dimensional

level set function and view the contour as its zero

level set. Then, instead of tracking the contour

points, we can track the zero level set of the level set

function. The advantage of doing so is that

topological changes can be naturally handled and the

geometric properties of the contour such as normal

vector and curvature can be calculated implicitly.

Therefore, the computational complexity is

decreased. Like the parametric deformable models,

speed functions should be properly defined. Malladi,

et al. (Malladi, et al, 1993) and Caselles, et al.

(Caselles, et al, 1997) first applied the level set

methods to medical images. Malladi’s model used

the gradient information as a stop criterion. The

definition of the speed is intuitive: when the contour

moves to the structure boundary, the increase of

gradient magnitude decreases the speed value

therefore slows down the contour. However, this

speed model suffered from leakage due to its mere

dependence on the gradient magnitude.

Unlike Malladi’s model, geodesic active contour

algorithm (Caselles, et. al, 1997) treated the

segmentation as an optimization problem of finding

the minimal distance curve. The moving equation of

GAC is also derived through energy functional.

While instead of solving directly the moving

equation, the contour is embedded in a level set

function and the moving equation then becomes a

level set equation. Geodesic active contour

algorithm showed a tight relationship between the

parametric model and the geometric model. The

introduction of level set representation in GAC

makes the algorithm flexible to handle the

topological changes. GAC and the later improved

GAC algorithms are applied to process the MR, CT

and ultrasound images like the tumour detection and

cardiac segmentation (Paragios, 2002). Another

popular geometric model Chan-Vese’s model is

based on a simplified version of Mumford-Shah

energy model (Chan and Vese, 1999). The most

appreciable advantage of Chan-Vese’s algorithm is

that it can obtain a boundary of discrete points,

which is quite useful for medical image applications

when the interested structures are represented by

discrete pixel clusters and have no clear definition of

boundaries.

3 DISCUSSIONS

When the interested structures have distinctive

quantifiable features, using threshold-based

algorithms is effective. Threshold-based algorithms

do not need complex operations therefore are

computationally efficient. However, due to their

dependence on thresholds, these algorithms are

sensitive to noises, hard to combine with spatial

information and difficult to be applied to multi-

channel images. As medical images are usually

noisy and suffer from intensity inhomogeneity, the

segmentation results of threshold-based algorithms

are usually far from satisfaction. Therefore these

algorithms are seldom used alone. Instead they are

often used as an efficient pre-segmentation step.

Compared with threshold-based algorithms, the

ones based on pattern recognition techniques can

better utilize structure information therefore can

achieve satisfied results. When the structures in

medical images are regular and not much influenced

by noises, applying pattern recognition techniques is

effective. However, like the threshold-based models,

pattern recognition models are also sensitive to

noises. The results of these algorithms may depend

on their initialization step. For the classifier-based

algorithms, the segmentation results depend on the

size of the training samples and the correctness of

the manual segmentations. For the clustering

algorithms, the number of clusters, the position of

the initial points and the parameters should be

properly selected. The lack of incorporating spatial

characteristics is also an obstacle. Due to the large

shape variations in medical images, the applications

of these algorithms are constrained.

Due to the advantages of being able to handle

structures with complex topology, easy to

incorporate with other techniques, sub-pixel

accuracy, noise insensitive and intuitive interaction

mechanisms, the deformable models are intensively

investigated in the last few decades. Parametric

deformable models have high computational

efficiency and are easy to incorporate with other

techniques; Geometric deformable models have the

advantage of naturally handling the topological

changes. For the medical image segmentation, using

parametric model or geometric model depends on

the applications. In general, when structures have

large shape variety or complicated topology,

geometric deformable models are preferred; when

the interested structures have open boundaries or the

structures are thin or the algorithms need real-time

operations, parametric models are preferred.

However, deformable models usually contain certain

number of parameters. To select proper parameters

is critical to the final segmentation results while this

is usually a time-consuming job.

CT images and MR images are widely used

modalities to study the organs in the pelvic cavity.

IMAGAPP 2009 - International Conference on Imaging Theory and Applications

138

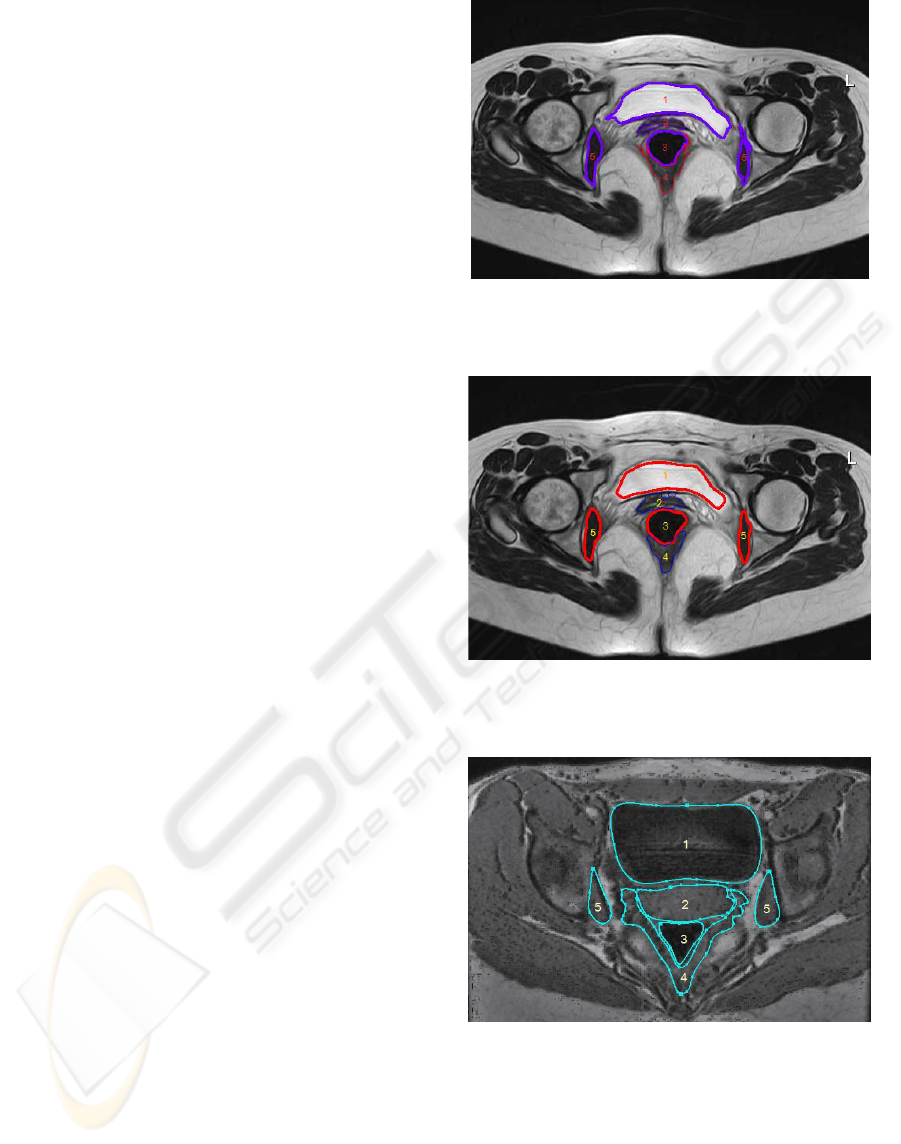
Figure 1 and Figure 3 illustrate the two imaging

models. Segmentation task includes sketching

bladder, urethra, vagina, rectum and pelvic floor.

The complex anatomical structures and the inter-

connectivity between organs make the segmentation

difficult to perform. We do not intend to propose

new algorithms here but use this example to make a

preliminary discussion of possible applications of

the three categories of algorithms.

Figure 1 illustrates the segmentation result of

region grow algorithm; Due to the high resolution

and signal-to-noise ratio, bladder and vagina can be

segmented successfully. While the boundary of the

right obturator internus is leaked due to the influence

of partial volume effect. Figure 2 illustrates the

segmentation result of geodesic active contour

algorithm. The boundaries of the obturator internus

are correctly segmented and the boundary of vagina

is not leaked in the upward direction. This is due to

the restriction of smoothness of the moving contours.

The structure boundaries are more regular than the

ones in Figure 1. While also due to this restriction,

small details of structure boundaries are eliminated

so that the boundaries of bladder and levator ani are

not complete. For the two segmentations, both

boundaries of levator ani are not satisfied. An

example of manual segmentation of levator ani is

illustrated in Figure 3. In fact, the segmentation of

levator ani muscles needs prior shape information

therefore a correct segmentation depends on

information beyond the presented images. This

feature is the advantage of the algorithms based on

pattern recognition techniques. For the CT images

which contain large amount of noises and low

spatial resolution of soft tissues, the priori shape

information is more important. The result of

applying watershed algorithm to images in Figure 3

is illustrated in Figure 4, from which we can see the

noise influence, the discontinuity and the difficulties

in this application. A possible way to design a new

algorithm can be incorporating the comparative

distances of different organs and use the prior shape

information to constrain the result.

4 CONCLUSIONS

As pointed out in Section 1, most of the algorithms

combine multiple segmentation techniques and use

diverse image cues to improve the segmentation

results. Therefore, a definite classification of an

algorithm may be infeasible. In this paper, we

classify the current algorithms into three categories

and summarize their features. From the discussions

we can see that each category has its suitable

Figure 1: Segmentation results of MR image using region

growing algorithm: 1-bladder, 2-vagina, 3-rectum, 4-

levator ani, 5-obturator internus.

Figure 2: Segmentation results of MR image using

geodesic active contour algorithm: 1-bladder, 2-vagina, 3-

rectum, 4-levator ani, 5-obturator internus.

Figure 3: Manual segmentation results of CT image: 1-

bladder, 2-vagina, 3-rectum, 4-levator ani, 5-obturator

internus.

application fields. For a concrete medical image

segmentation task, researchers should combine the

application background and practical requirements

to design proper algorithms. Accuracy, complexity,

efficiency and interactivity of a segmentation

algorithm should all be the considered factors.

A REVIEW ON THE CURRENT SEGMENTATION ALGORITHMS FOR MEDICAL IMAGES

139

Figure 4: Segmentation results of CT image using

watershed algorithm.

ACKNOWLEDGEMENTS

This work was partially done in the scope of the

project “BIOPELVIC-Study of Female Pelvic Floor

Disorders”, with reference PTDC/SAU-

BEB/71459/2006, financially supported by

Fundação para a Ciência e a Tecnologia of Portugal.

REFERENCES

Adams, R., Bischof L., 1994. Seeded Region Growing.

IEEE Trans. on Pattern Anal Mach. Intelligence,

16:641-47.

Akselrod-Ballin, A, Galun, M, et al, 2006. Atlas Guided

Identification of Brain Structures by Combining 3D

Segmentation and SVM Classification. Int. Conf Med

Image Comput Comput Assist Interv., 209-16.

Alirezaie, J., Jernigan, M. E., Nahmias, C., 1997. Neural

Network-Based Segmentation of Magnetic Resonance

Images of the Brain, IEEE Trans. on Nuclear Science,

44:194-8.

Bezdek, J. C., Hall, L. O., Clarke, L. P., 1993. Review of

MR Image Segmentation Techniques Using Pattern

Recognition, Med. Phys., 20:1033-48.

Canny, J., 1986. A Computational Approach to Edge

Detection. IEEE Trans. Pattern Analysis and Machine

Intelligence, 8:679-714.

Caselles, V., Kimmel, R., Sapiro, G., 1997. Geodesic

Active Contours. Int. J. of Comp. Vision, 22:61-79.

Chan, T., Vese, L. A., 1999. An Active Contour Without

Edge. Int. Conf. Scale-Space Theories in Computer

Vision, 141-151.

Cheng, K. S., Lin, J. S., Mao, C. W., 1996. The

Application of Competitive Hopfield Neural Network

to Medical Image Segmentation. IEEE Trans. on Med.

Img., 15:560-7.

Cohen, L. D., 1991. On Active Contour Models and

Balloons. CVGIP: Image Understanding, 53:211-8.

Cootes, T. F., Edwards, G. J., Taylor, C. J., 2001. Active

Appearance Models. IEEE Trans. Pattern Analysis

and Machine Intelligence, 23: 681-85.

Davis, L. S., 1975. A Survey of Edge Detection

Techniques. Comp. Graphics and Image Processing,

4:248-70.

Flitti, F., Collet, C., Joannic-Chardin, A., 2005.

Unsupervised Multiband Image Segmentation Using

Hidden Markov Quadtree and Copulas. IEEE Int. Conf.

on Image Processing, 2:634-37.

Gindi, G., Rangarajan, A., Zubal, G., 1993. Atlas-Guided

Segmentation of Brain Images via Optimizing Neural

Networks. Proc. SPIE Biomedical Image Processing

IV, 1905-58.

Kass, M., Witkin, A., Terzopoulos, D., 1987. Snakes:

Active contour models. Int. J. of Comp. Vision, 1:321-

31.

Malladi, R., Sethian, J. A., Vemuri, B., 1993. A Topology

Independent Shape Modeling Scheme. SPIE Conf. on

Geometric Methods in Computer Vision II, 2031:246-

58.

McInerney, T., Terzopoulos, D., 1995. A Dynamic Finite

Element Surface Model for Segmentation and

Tracking in Multidimensional Medical Images with

Application to Cardiac 4D Image Analysis.

Computerized Medical Imaging and Graphics, 19:69-

83.

Mohamed, N. A., Ahmed, M. N., Farag A., 1998.

Modified Fuzzy C-mean in Medical Image

Segmentation. Proceedings of the 20th Annual

International Conference of the IEEE

, 3:1377-80.

Ng, H. P., Ong, S. H., et al, 2006. Medical Image

Segmentation Using K-Means Clustering and

Improved Watershed Algorithm. IEEE Southeast

Symposium on Image Analysis and Interpretation, 61-

Osher, S., Sethian, J., 1988. Fronts Propagating with

curvature-dependent speed: algorithms based on

Hamilton-Jacobi formulations. J. Comp. Phys., 79: 12-

49.

Paragios, N., 2002. A Variational Approach for the

Segmentation of the Left Ventricle in Cardiac Image

Analysis, International Journal of Computer Vision,

50:345-62.

Pohle, R., Toennies, K. D., 2001. Segmentation of

Medical Images Using Adaptive Region Growing,

SPIE, 1337-46.

Wang, S., Zhu, W. Y., Liang, Z. P., 2001. Shape

Deformation: SVM Regression and Application to

Medical Image Segmentation, Eighth International

Conference on Computer Vision, 2:209-16.

Wong, K. P., Feng, D., et al, 2002. Segmentation of

Dynamic PET Images Using Cluster Analysis. IEEE

Trans. on Nuclear Science, 40:200-07.

Xu, C. Y., Prince, J. L., 1998. Snakes, Shapes, and

Gradient Vector Flow. IEEE Trans. on Image

Processing, 7:359-69.

Zaidi, H., 2005. Quantitative Analysis in Nuclear

Medicine Imaging, Springer.

IMAGAPP 2009 - International Conference on Imaging Theory and Applications

140