THE EMERGENT STRUCTURE OF THE DROSOPHILA WING
A Dynamic Model Generator
Alberto Silletti
Department of Information Engineering, University of Padova, Via Gradenigo 6A, Padova, Italy
Angelo Cenedese
Department of Engineering and Management, University of Padova, Vicenza, Italy
Alessandro Abate
Department of Aeronautics and Astronautics, Stanford University, Stanford (CA), U.S.A.
Keywords:
Structure detection, Graphical model, Random walk, Drosophila wing, Morphogenesis.
Abstract:
Drosophila melanogaster is a model organism in genetics thanks to the compactness of its genome and its
relative simplicity. Recently, certain developmental patterns in Drosophila have been studied by mathematical
models, with the aim of gaining deeper and quantitative insight into the morphogenesis of this insect. There
is a need for accurate dynamical of the epithelial cell structure and organization within the fly wing, to further
the understanding of a phenomenon known as planar cell polarity. The present study tackles the problem of
retrieving such a salient structure using classical tools of dynamical system theory embedded with network
and graph concepts. On the one hand the goal is to provide a visual detection and representation of the cell
packaging that is accurate and fine. Particular care is also put in obtaining a model of this structure, whose
main features are the compactness and simplicity.
1 INTRODUCTION
Drosophila melanogaster is a model organism in de-
velopmental biology. Scientific interest in this organ-
ism can be traced back to some early work in genetics,
and more recently the understanding of this insect has
progressed with the investigation of its early devel-
opment and the sequencing of its relatively compact
genome. The relative simplicity of its morphogenesis
allows to edulcorate the study of its developmentfrom
many complications. Many human disease genes can
be investigated and understood through analogues in
the fruit fly. An important issue for the fly morpho-
genesis is the study of the polarization of cells on
its wing. A mechanistic approach to study this phe-
nomenon has led to some understanding of the un-
derlying structures and regulatory proteins in the ep-
ithelial cells of the fly wing (Amonlirdviman et al.,
2005). The dynamical model hinges on the assump-
tion that the cell are regularly packed in a honeycomb
structure throughout the wing. In order to understand
how to extend these models, it makes sense to infer
the structure and motion of the network of epithelial
cells by looking at the phenotype of the fly wing with
movies taken in the laboratory. This suggests to split
the approach into two sequential steps:
1. first, given a single frame of the fly wing, build a
network that closely represents the cell packing;
2. then, given a movie (a sequence of frames) of the
fly wing, correlate the networks generated by con-
sidering single frames into a time-dependent dy-
namical model.
In this article we report on the former point, while the
extension of the study is currently under investigation.
The goal of this study is twofold. On the one
hand we try to detect the structure on the drosophila
wing and provide a visual representation. On the
other hand, we produce a model of the same struc-
ture, whose main features are the compactness and
the simplicity.
406
Silletti A., Cenedese A. and Abate A. (2009).
THE EMERGENT STRUCTURE OF THE DROSOPHILA WING - A Dynamic Model Generator.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 406-410
DOI: 10.5220/0001795804060410
Copyright
c
 SciTePress

Figure 1: Drosophila wing epithelial cells.
The following approach is thus developed both to
retrieve the network structure as a fine representation
and to abstract the information related to the structure
into a manageable model. This is obtained by explor-
ing the visual data through a dynamic random walk
model, whose motion state summarizes the useful in-
formation and allows the full detailed reconstruction
of the network. To give a pictorial idea, the image
frame is considered as a landscape where clear paths
have to be discerned from darker areas. The agent
performing the detection advances by scanning the
neighborhood of his current position in search for ex-
plorable paths. When a bifurcation occurs the agent
generates one or more siblings that start to move in-
dependently, until the whole frame has been explored.
The remainder of the paper is organized as fol-
lows. After an overviewof the state of the art in struc-
ture detection (Sec. 2) and a description of the pro-
cedure for image preprocessing (Sec. 3), the adopted
model is introduced in Sec. 4 and the algorithm ex-
plained in Sec. 5. Then, the static analysis of the im-
age frame is discussed in Sec. 6 and, finally, in Sec. 7
some conclusions are drawn and insight on future de-
velopments is given.
2 THE STATE OF THE ART
The recognition of structures in digital images is a
crucial task in many automated algorithms used in
computer vision. For the task of edge detection,
several approaches based on derivatives have been
proposed, among which the seminal studies by So-
bel (Sobel, 1968) and Prewitt (Prewitt, 1970) and
Canny (Canny, 1986).
These approaches though are prone to failure,
since they do not incorporate any prior knowledge of
the object, nor do they include any geometrical model.
This can yield very fragmented edges and many false
classifications. They also do not return any com-
pact and light representation of the recognized pat-
tern. Such algorithms are good to represents patterns,
but not to model them. The Canny edge detector out-
puts a bitmap map, where each pixel is classified as
belonging to a border or not. Indeed, no structure is
returned, and no compact model is given to the user.
If there is a need for computing metrics or for analyti-
cally following a path around the edges, this approach
appears to be unsatisfactory.
Active Contours (Blake and Isard, 1998) based
approaches give better results, thanks to the elastic
model structure they incorporate. Active Contours
and Deformable Models (McInerney and Terzopou-
los, 1996) generally perform well in shape recogni-
tion. Still, they are very sensitive to noise, they need a
good initialization point to converge, and they require
hard-tuning of the parameters to make things really
work.
For thin linear structures such as vessels, mar-
ble veins, roads on terrain, better results can be
achieved using a model of the motion over the im-
age, which attempts to follow the structure of interest
(Grisan et al., 2003). This approaches is promising
and achieves near optimal results. A random motion
paradigm can also be used also for image segmen-
tation (Harel and Koren, 2001) and image enhance-
ment (Smolka and Wojciechowski, 2001).
3 IMAGE PREPROCESSING
The images retrieved from biological experiments
are particularly noisy and exhibit poor contrast, with
non-uniform background illumination, resulting in
structure boundaries not sufficiently sharp to be seg-
mented. The preprocessing stage presented consists
of four sequential steps (see Fig.2):
1. the image is filtered with a low-pass gaussian filter
to soften high frequency noise;
2. an erosion filter suppresses the isolated bright pix-
els and decreases the intensity of cell edges, while
retaining all the significant information;
3. an histogram stretch allows to partially recover the
color dynamic range;
4. an image intensity power enhances the contrast.
4 THE DYNAMICAL MODELS
In this section the principle underlying the algorithm
is briefly described. To retrieve the salient structure in
the video sequence and to circumvent issues related
to disconnected edges and false recognition (such as
those mentioned in Sec. 2), the edge detection prob-
lem is re-interpreted as the problem of exploring a
digital frame in search of the connected tracks. Each
THE EMERGENT STRUCTURE OF THE DROSOPHILA WING - A Dynamic Model Generator
407

(a) (b)
Figure 2: Image preprocessing: original (a) and prepro-
cessed (b) frames.
digital picture is viewed as a landscape that has to
be explored and where bright pixels–belonging to the
edges of the cells–are thought of as roads, and dark
pixels–the interior of the cells–as unexplored loca-
tions.
The idea behind the algorithm for robust and fast
reconstruction of the interesting structure is based on
a two level model, referred to respectively as an ex-
plorer agent system and as a network agent system.
The explorer agent will retrieve the structure and pro-
vide a visual representation as fine as possible, while
then network agent will abstract a compact model.
An explorer agent system A is defined according
to a walk model, whose state equation is:
p(t + 1) = p(t) + g(θ(t)) , (1)
p(t) =

x(t)
y(t)

∈ L,
p(t) is the current point position on the discrete do-
main L ⊂ Z
2
of the image frame and g(·) is a motion
function. In the specific case,
g(θ(t)) = k

sin(θ(t))
cos(θ(t))

,
k being a design constant and θ(t) being the heading
direction, which assumes the role of the input to the
agent system.
The observation equation is the following:
y(t) =


x(t)
y(t)
θ(t)


=


1 0
0 1
0 0


p(t) +


0
0
1


θ(t).
Several instances of the explorer agent,
{A
i
, i = 1, . . . , N
A
}, are concurrently present in
the field of vision, and each generates at any time one
or more directions viable to advance the exploration.
Precisely, for each A
i
the set of possible directions

θ
i, j
, j = 1, . . . , m
i

, originating new agents, are
collected in the vector Θ
i
∈ R
m
i
.
Globally, the observations y(t) of all the explorer
agents A
i
yield a graph model G = (N ,E) (being
N and E nodes and edges, respectively), where each
node n
i
∈ N is characterized by the state { x, y, Θ} of
the locations visited by one of the A
i
, and the edges
keep track of the path traveled by each agent (see
Fig. 3). This graph provides a good representation
of the retrieved structure, in the sense suggested in
Section 2.
(a) (b)
Figure 3: Representation and Model graphs G (a) G
r
(b).
For modeling purposes, the goal is to obtaining
compact-size models, flexible and agile. In this re-
spect, only the subset N
r
of the nodes associated to
non-scalar Θ (and the correspondent edges E
r
) are in-
teresting in the description, that is:
G
r
= (N
r
, E
r
) N
r
⊂ N s.t. dim(Θ(n
i
)) > 1∀n
1
∈ N
r
,
where dim(Θ(n
i
)) indicates the cardinality of vector
Θ for node n
i
. If the border effects are neglected, the
resulting graph G
r
is a 3-connected graph, in which
the minimum vertex degree is d = 3.
4.1 Brightness Function
We now explain how to choose the input direction
θ(t). With reference to the pictorial interpretation,
the aim is to explore the surroundings of the current
position and to move from a bright location to an-
other bright location. Thus a good direction of move-
ment will be a direction that maximizes some sort of
brightness function. Local brightness information is
obtained by means of a function L(θ) : [0, 2π) → R
built with the specific purpose of finding good direc-
tions of exploration. Sectors centered on the current
position p are spanned, and for each sector the aver-
age brightness is computed. Formally, given a sector
Ω
i
, with any generic shape, we have
L(θ
i
) =
R
Ω
i
I(ω)dω
R
Ω
i
dω
(2)
A natural choice for Ω
i
is circular sector. Sectors
of different shapes can also be built: For the problem
of interest rectangular sectors also result to be quite
effective.
After smoothing and thresholding the function, lo-
cal maxima are collected as putative direction for the
motion. Let Θ = {θ
1
, θ
2
, ·, θ
n
} = arg max
θ
L(θ).
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
408

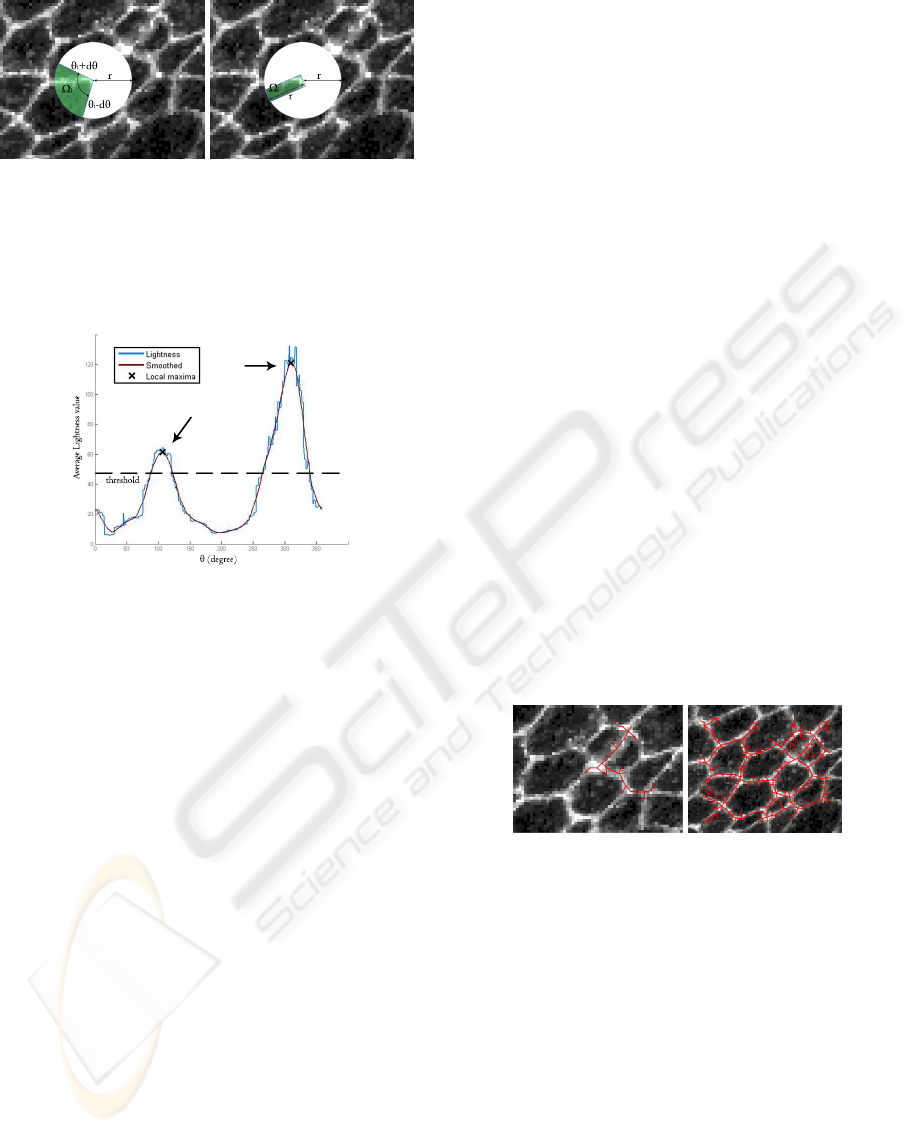
(a) (b)
Figure 4: A brightness function built on circular sectors is
a natural choice, since it mimics the field of view of human
beings (a). Other shapes for sectors are also possible, de-
pending on the problem under study: in the specific case, a
rectangular shape efficiently serves the purpose (b).
Figure 5: Local maxima of the brightness function identify
candidate directions of expansion.
5 THE ALGORITHM
The initialization of the algorithm consists of a single
agent A
0
exploring the frame. At each motion step,
the arguments of local maxima of L provide the set Θ
of candidate directions. A Priority Queue Q is defined
by inserting either the agent A
0
with its heading direc-
tion and its corresponding brightness value or, when
multiple directions m
i
are possible, instances of A
0
along with the direction θ
i
∈ Θ. Each of these agents
is then put in motion according to Eq. 1.
The priority queue is sorted according to the
brightness function associated with the current loca-
tion of each agent. At each iteration step, the agent A
i
with the highest brightness value is extracted and the
exploration process is iterated. The role of the prior-
ity queue is thus to keep in memory the front of the
expansion, and at the same time, to give the best pos-
sible expansion point, in the sense that the first agent
in the queue will move to the best (i.e. brightest) area
of the image.
By doing so, the algorithm is building a graph G,
where each node is the location p
i
of an agent A
i
ex-
tracted from the priority queue, and each arc joins a
node and its nearest ancestor. Interpreting the under-
lying structure of the walk as a graph allows to resort
to graph theory (Cormen et al., 1990) to refine the
procedure.
5.1 Graph Structure Refinement
Small loops have to be avoided. Small loops are fre-
quent in extensive bright areas of the image, where
the brightness function L(θ) is not prone to differenti-
ate between redundant directions. In these situations,
a direction is as likely as any other, and the choice
is driven mainly by randomness. When this happens
we get |Θ| >> 1 and θ
i
≈ θ
i+1
∀ θ
i
∈ Θ. In other
words, all the values of θ
i
∈ Θ are very similar and
these directions spans uniformly the surrounding en-
vironment, so there is no particular reason to pick one
direction over another.
In order to avoid this, after extracting a point from
the queue, it is tested for loop creation in the graph.
Large loops are accepted because they correspond to
an actual closed path (for instance the perimeter of a
cell), while small loops are disregarded.
A joining procedure is then required to fill small
gaps: If two valid agents A
i
and A
j
end up close to
each other, | {x, y}
i
− {x, y}
j
| < ε, they are joined to-
gether.
The algorithm also marks as boundary nodes
those nodes close to the boundary of the digital im-
age: The expansion process ends there (see Fig. 6(b))
and the agent A
i
stops.
(a) (b)
Figure 6: (a) Small loops are frequent and are mainly due to
the locality feature of the brightness function. (b) Raw re-
sults before postprocessing: many small spurious branches
span over the interior of the cells.
The expansion process could create dead-
branches, characterized by extremal non-border
nodes of degree 1. A polished graph is obtained it-
eratively removing all such nodes and related edge.
occurs.
The network agent system reconstruct the final ge-
ometric model of the cells considering only nodes
with degree d > 2 and border nodes, considered the
corner of the cells. The new graph G
r
consists of such
corners and new edges created between them if in the
original graph there was a straight path (a path con-
THE EMERGENT STRUCTURE OF THE DROSOPHILA WING - A Dynamic Model Generator
409

necting them not passing through any other corner).
The model reconstruction thus prunes a lot of nodes
and edges and ends up with a light, compact represen-
tation of the cellular structure, achieving the second
goal of this paper.
6 STATIC ANALYSIS
Preliminary results show a good accuracy in retriev-
ing the salient structure on the fly wing and robust-
ness in the detection procedure, for all the tested se-
quences. In Fig. 7 results obtained with the proposed
technique are shown. The two cases are indicative of
the critical issues that need to be faced, such as non-
uniform illumination, differentradii of the cells, noisy
images.
(a) (b) (c)
(d) (e) (f)
Figure 7: Example frames: a) -b) original; c) -d) represen-
tation G; e) -f) model G
r
.
It is interesting to show the dynamic evo-
lution of the exploration of the frame. A
video showing the full procedure can be found at
http://www.youtube.com/watch?v=I2HfKTCEd6w.
7 CONCLUSIONS AND FUTURE
DEVELOPMENTS
In this work a procedure to detect salient lattice fea-
tures from biological images has been developed,
with the twofold purpose of representation and mod-
eling. So far, the problem of the static reconstruction
from single frames has been addressed, with encour-
aging results both for the accuracy of the details and
for the robustness of the technique.
As a first step towards the dynamic reconstruction
and tracking will be obtained by simply applying sev-
eral times, once per frame, the static analysis (Sec. 6).
A video obtained through this approach is available
at http://it.youtube.com/watch?v=WxWjZSvuoh4. A
fully dynamic tracking is still under study, and more
refined dedicated approaches will be developedby ex-
ploiting temporal and local coherence.
REFERENCES
Amonlirdviman, K., Khare, N., Tree, D., Chen, W., Axel-
rod, J., and Tomlin, C. (2005). Mathematical model-
ing of planar cell polarity to understand domineering
nonautonomy. Science, 307:423–426.
Blake, A. and Isard, M. (1998). Active Contours. Springer-
Verlag, New York, USA.
Canny, J. (1986). A computational approach to edge detec-
tion. IEEE Trans Patter Analysis and Machine Intelli-
gence, 8(6):679–698.
Cormen, T., Leiserson, C., and Rivest, R. (1990). Introduc-
tion to Algorithms. The MIT Press and McGraw-Hill.
Grisan, E., Foracchia, M., and Ruggeri, A. (2003). A novel
method for the automatic grading of retinal vessel tor-
tuosity. Engineering In Medicine and Biology Society.
Proc. of the 25th Annual International Conference of
the IEEE, 1(1):866–869.
Harel, D. and Koren, Y. (2001). On clustering using random
walks. Proc. of the 21st Conference on Foundation of
Software Technology and Theoretical Computer Sci-
ence, 2245(1):18–41.
McInerney, T. and Terzopoulos, D. (1996). Deformable
models in medical image analysis: a survey. Medical
Image Analysis, 1(2):91–108.
Prewitt, J. (1970). Object enhancement and extraction in
Picture Processing and Psychopictorics. Academic
Press, New York.
Smolka, B. and Wojciechowski, K. (2001). Random walk
approach to image enhancement. Signal Processing,
81:465–482.
Sobel, I. (1968). A 3x3 isotropic gradient operator for im-
age processing. Unpublished, presented in a talk a the
Stanford Articifial Project.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
410