ON ANALYZING SYMMETRY OF OBJECTS USING ELASTIC

DEFORMATIONS

Chaﬁk Samir

†

, Anuj Srivastava

, Mohamed Daoudi

and Sebastian Kurtek

†

Mathematical engineering department, UCL, Louvain-la-neuve, 1348, Belgium

Department of Statistics, FSU, Tallahassee, FL 32306, U.S.A.

Institut TELECOM ; TELECOM Lille1 LIFL UMR 8022, 59650 Villeneuve d’Ascq, France

Keywords:

Symmetry of 2D and 3D objects, Shape analysis, Elastic deformations, Optimal deformation, Facial shapes,

Geodesic path, Nearest symmetric shape, Measure of asymmetry.

Abstract:

We introduce a framework for analyzing symmetry of 2D and 3D objects using elastic deformations of their

boundaries. The basic idea is to deﬁne spaces of elastic shapes and to compute shortest (geodesic) paths

between the objects and their reﬂections using a Riemannian structure. Elastic matching, based on optimal

(nonlinear) re-parameterizations of curves, provides a better registration of points across shapes, as compared

to the previously-used linear registrations. A crucial step of orientation alignment, akin to ﬁnding planes

of symmetry, is performed as a search for shortest geodesic paths. This framework is fully automatic and

provides: a measure of asymmetry, the nearest symmetric shape, the optimal deformation to make an object

symmetric, and the plane of symmetry for a given object.

1 INTRODUCTION

Symmetry is an important feature of an object and in

symmetry analysis one asks questions of the type: Is

a given object symmetric? What is the level (quan-

tiﬁcation) of asymmetry in an object? What is the

nearest symmetric object for a given asymmetric ob-

ject and how far is it? How to minimally deform an

object to make it symmetric? What are the planes(s)

of symmetry of a given symmetric object? And so on.

Such an analysis plays an important role in several

applications, including object design, manufacturing,

packaging, segmentation (Simari et al., 2006), view

selection (Thrun and Wegbreit, 2005), model reduc-

tion (Mitra et al., 2006), medical diagnosis, and sur-

gical planning. Reﬂection symmetry occurs in many

biological objects, and is an important part of how

we as humans perceive them. Symmetry analysis can

also play an important role in medical diagnostics, for

example, when the level of asymmetry in an organ re-

lates to its health. The proceduresfor quantiﬁcation of

asymmetry, estimation of symmetry hyperplane, and

symmetrization of objects are also gaining attention

in 3D graphics, object recognition, indexing and re-

trieval.

In this paper we will consider both 2D and 3D ob-

jects, and we will restrict to the shapes of their bound-

aries for symmetry analysis. For the 2D case, we

will study a variety of objects from public databases,

but for the 3D case we will focus on shapes of facial

surfaces. Symmetry of faces has large relevance in

multiple contexts. For example, in orthodontics, see

for example (Tomaka, 2005), that symmetry analysis

can help plan surgical interventions in the craniofa-

cial area and to monitor their long-term effects. The

detection of facial landmarks can beneﬁt from a sym-

metry analysis. An important component of cosmetic

facial surgeries is to enhance facial symmetries, long

considered a factor in improving appearances. A sur-

geon can be guided by the optimal deformation of a

face that will make it symmetric.

By deﬁnition, a solid or a surface is reﬂection-

symmetric if its reﬂection, with respect to a certain

plane, is identical to it. Consequently, classifying an

object as symmetric or not, or measuring the level of

its asymmetry, can be reduced to the task of comput-

ing differences in shapes between two objects: the

original one and its mirror reﬂection. Several recent

efforts in shape analysis have focused on symmetry

detection of 2D and 3D shapes (Mitra et al., 2006),

(Martinet et al., 2006), (Kazhdan et al., 2004). The

general framework used is as follows: Let β be an ob-

194

Samir C., Srivastava A., Daoudi M. and Kurtek S. (2009).

ON ANALYZING SYMMETRY OF OBJECTS USING ELASTIC DEFORMATIONS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 194-200

DOI: 10.5220/0001797201940200

 SciTePress

ject (curve, surface, etc) in an appropriate R

and R be

a plane of reﬂection in R

. R will be denoted by the

vector v ∈ R

perpendicular to R. Assuming that β is

centered in that coordinate system, deﬁne a measure

of asymmetry as:

ρ(β) = argmin

v∈R

kβ−H(v)βk

, H(v) = (I −2

), (1)

where k·k is the two norm integrated over the points

in the object. H(v) is the Householder reﬂection op-

erator which rotates any vector into its reﬂection in a

plane orthogonal to v. In case ρ(β) is zero, the ob-

ject is said to be symmetric and the corresponding v

provides the the plane of symmetry. Zabrodsky et al.

(Zabrodsky et al., 1995) suggested a slightly differ-

ent formulation where they ﬁnd the nearest symmetric

object to the given object. That is, deﬁne

SD(β) = argmin

v∈R

,s.t. H(v)α=α

kβ −αk

. (2)

This idea has been called the symmetry distance

(Zabrodsky et al., 1995). Mitra et al. (Mitra et al.,

2007) formulate the search for symmetrization defor-

mation in a similar way, but based on points sampled

from the original model. Sun et al. (Sun and Sherrah,

1997) proposed a method to detect symmetry based

on the Extended Gaussian Image (EGI).

Since symmetry analysis is intimately tied to

quantiﬁcation of differences in shapes of objects and

their reﬂections, one should look more carefully at

how shape quantiﬁcation is being performed. It is

a common trend in papers on symmetry to use Eu-

clidean norms between points sets to form cost func-

tions. Additionally, the authors have invariably used a

linear registration of points, between the original ob-

ject and its reﬂection, to evaluate these norms. In con-

trast, the literature in shape analysis of curves sug-

gests a larger variety of metrics and nonlinear reg-

istrations in measuring shapes (Michor and Mum-

ford, 2006). In particular, the use of elastic defor-

mations to compare and analyze shapes is gaining

popularity. Here, the curves are allowed to optimally

stretch/shrink and bend to match one another during

comparisons. Mathematically, this is accomplished

by applying all possible re-parameterizations, includ-

ing nonlinear registrations, on curves to ﬁnd the opti-

mal registration. In this paper, we utilize the frame-

work of Joshi et al. (Joshi et al., 2007a), on elastic

shape analysis of curves, for performing symmetry

analysis of 2D shapes. To extend this idea to sym-

metry analysis of surfaces, we use the approach of

Samir et al. (Samir et al., 2006) where a facial sur-

face is represented as a collection of level curves, and

faces can be elastically compared by comparing the

corresponding curves.

The rest of this paper is organized as follows. We

present the general framework in Section 2, particu-

larize it for 2D shapes in Section 3 and for surfaces in

Section 4.

2 GENERAL FRAMEWORK

We advocate the use of geometric approaches in sym-

metry analysis. In particular, we suggest the use of

elastic shape analysis of curves and surfaces to help

quantify differences between objects and their reﬂec-

tions. A geometric approach for shape analysis in-

volves: (i) deﬁning a space of shapes using their

mathematical representations, (ii) imposing a Rie-

mannian structure on it, and (iii) numerically com-

puting geodesic paths between arbitrary shapes. Care

is taken to remove symmetry-preserving transforma-

tions from the representation using algebraic equiva-

lences.

More precisely, one starts with a space, say C , of

mathematical representations of objects, e.g. closed

curves, and studies its differential geometry to iden-

tify tangent spaces TC . Then, choosing a Riemannian

metric – a positive-deﬁnite, bilinear, symmetric form

on tangent spaces – one can deﬁne lengths of paths

on C . Given any two objects, i.e. two elements of C ,

one can use a numerical approach to ﬁnd a shortest

geodesic path between them. Let d

denote the length

of this geodesic.

Symmetry of a curve or a surface is invariant to its

translation, scaling, rotation, and re-parametrization.

Scaling and translation are usually accounted for in

deﬁning C , but the other two are handled explicitly as

follows. One deﬁnes the action of the rotation group

SO(n) and the re-parametrization group Γ on C , and

deﬁnes the orbits of objects under these actions as

equivalence classes. In other words, for a q ∈ C, if

[q] is the set of all variations of q obtained by rotat-

ing and re-parameterizing it, then [q] is deﬁned to be

an equivalence class. The set of all such equivalence

classes is the quotient space S = C /(SO(n)×Γ). The

distance between any two elements of S , say [q

] and

], is the length of the shortest geodesic in C be-

tween elements of those two sets:

([q

],[q

]) = inf

∈[q

],p

∈[q

]

, p

)

= inf

∈[q

]

, p

) . (3)

The last equality assumes that SO(n) and Γ act on C

as isometries. The distance d

is invariant to rotation,

ON ANALYZING SYMMETRY OF OBJECTS USING ELASTIC DEFORMATIONS

195

translation, scaling, and re-parametrization of the ob-

jects. How can this distance be used to measure the

symmetry of an object? The answer comes from the

following result.

Theorem 1. 1) 2D Case. Assuming a simple, closed

curve β is bounded, and

β is an arbitrary reﬂection of

β, then the distance d

between β and

β is zero if and

only if β is symmetric.

2) 3D Case. For a two-dimensional surface S in R

if the distance d

between S and any of its reﬂection

S is zero, then there exists a rigid motion taking S to

S. In fact, this rigid motion is a composition of a re-

ﬂection in some plane, and a rotation around an axis

perpendicular to that plane.

We note that this theorem actually holds for any

bounded point set in R

or R

, although in this paper

we are concerned only with curves and surfaces.

This motivates the use of elastic distance d

as a

measure of asymmetry in an object. If an object is

perfectly symmetric, the distance d

, between itself

and its arbitrary reﬂection, will be zero. If it is not

symmetric then we can use d

as a measure of asym-

metry in that object. In the next two sections, we par-

ticularize this idea to analyze symmetries of 2D and

3D shapes.

3 SYMMETRY ANALYSIS OF 2D

CURVES

We start this section by summarizing the geometric

shape analysis of planar closed curves. Consider a

closed curve as a mapping β from S

to R

. To ana-

lyze its shape, we will represent this curve by a func-

tion q : S

→ R

, where q(t) =

β(t)

√

β(t)||

. Here, s ∈ S

where k·k is the usual two norm in R

. Given a q

function, we can reconstruct the original curve up to a

translation. We narrow our study to closed curves of

length one by deﬁning:

C = {q|

kq(t)kdt = 1,

q(t) ||q(t)||dt = 0} . (4)

The ﬁrst constraint forces the curves to be of length

one and the second constraint ensures their closure.

Shapes of curves are compared using geodesic paths

on C which, in turn, requires a Riemannian struc-

ture. To impose a Riemannian metric on C , de-

ﬁne the inner product: for any u,v ∈ T

(C ), hu,vi =

2π

hu(t),v(t)i dt. For computing geodesic paths on

C , there are a variety of numerical approaches avail-

able. In this paper we use a path-straightening ap-

proach, where the given pair of shapes is connected

by an initial arbitrary path in C and that path is itera-

tively “straightened” until it becomes a geodesic. For

details of implementation, please refer to the paper by

Joshi et al. (Joshi et al., 2007a). Let d

) be the

length of geodesic connecting q

and q

in C .

Since the symmetry of β is considered invariant

to its rotation or re-parametrization, our measure of

asymmetry should also be invariant to these trans-

formations. (Note that translation and scaling of a

curve have already been removed when curves are

represented as elements of C .) The rotation of a

curve is represented by a 2 ×2 matrix, an element

of SO(2), while a re-parametrization is a diffeomor-

phism γ : S

→ S

, an element of Γ, the space of all

such diffeomorphisms. Deﬁne the actions of SO(2)

and Γ on C as follows:

SO(2) × C →C , (O,q) = {Oq(t)|t ∈ [0, 1]}

Γ × C →C , (γ,q) = {

γq(γ(t))|t ∈ [0,1]}

It can be shown that these two group actions com-

mute and, hence, we can deﬁne the quotient space

with respect to their direct product according to S =

C /(SO(2) ×Γ). The orbit of a shape, represented by

q, is given by:

[q] = {

γOq(γ(t))|O ∈ SO(2),γ ∈ Γ} ,

and this denotes the equivalence class of all rotations

and re-parameterizations of q. The set of all such

equivalence classes is S .

To compute distances between any two elements

of S , one has to ﬁnd the shortest path between the

two corresponding orbits. This length of this shortest

path is:

= inf

O∈SO(2),γ∈Γ

γOq

(γ)) . (5)

This minimization requires search over all rotations

and re-parameterizations of q

so that it best matches

. Note that if q

is a reﬂection of q

, then the op-

timization over SO(2) is similar to the one in Eqn.

1, except that the Euclidean norm is replaced by the

geodesic distance d

. The other difference from that

equation is the optimization over γ, which allows for

nonlinear registration between the two shapes. How

to solve this optimization problem? Joshi et al. (Joshi

et al., 2007b) describe a technique that uses gradients

to search over Γ but uses an exhaustive search over

SO(2) to minimize the cost function. We refer the

reader to that paper for details.

To analyze the level of asymmetry of a closed

curve β, we obtain a reﬂection

β = H(v)β, where

H(v) = (I −2

), for any v ∈ R

. Denote the rep-

resentation of β in C by q and that of

β by ˜q. Let

ψ : [0,1] 7→ S be the geodesic path between q and ˜q

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

196

bone bird bottle brick camel cat car carriage

chopper crown fountain stef rat fork tool ﬂatﬁsh glass

Figure 1: Seventeen 2D shapes used in experiments on symmetry.

0 1 2 3 4 5 6

Figure 2: In each row, the left panel shows β and

β, the middle panel shows geodesic ψ

between them, and the last panel

shows the optimal γ for their matching.

constructed using optimization techniques presented

in (Joshi et al., 2007b); we have ψ(0) = q and ψ(1) =

˜q. ψ provides important information about the sym-

metry of β:

1. Measure of Asymmetry. Deﬁne the length of the

path ψ as a measure of asymmetry of β:

ρ(β) = d

(q,H(v)q)) , for any v ∈R

. (6)

2. Nearest Symmetric Shape. The halfway point

along the geodesic, i.e. ψ(0.5), is perfectly sym-

metric. Amongst all perfectly symmetric shapes,

it is the nearest to q in S .

3. Deformation for Symmetrization. The velocity

vector

ψ(0) provide a deformation (vector) ﬁeld

on β than transforms β into the nearest symmetric

shape.

Next we present some experimental results on

measuring asymmetry on some 2D shapes taken from

one of the Kimia databases. We have used seven-

teen curves from different shape classes; these curves

are shown in Figure 1. Based on their appearances,

one can see that some curves show strong symmetries

while others look far from symmetric.

Our approach is to take a curve β, select an ar-

bitrary reﬂector in R

, and form a new curve

β by

applying that reﬂector on β. Shown in the left col-

umn of Figure 2 are four examples of such random re-

ﬂections. The last shape is an artiﬁcially constructed

shape with perfect symmetry, just to test the algo-

rithm. Then, we compute geodesic paths in S between

the shapes of q and ˜q, the representatives of β and

β in C . Four examples of these paths are shown in

the middle column of Figure 2. The lengths of these

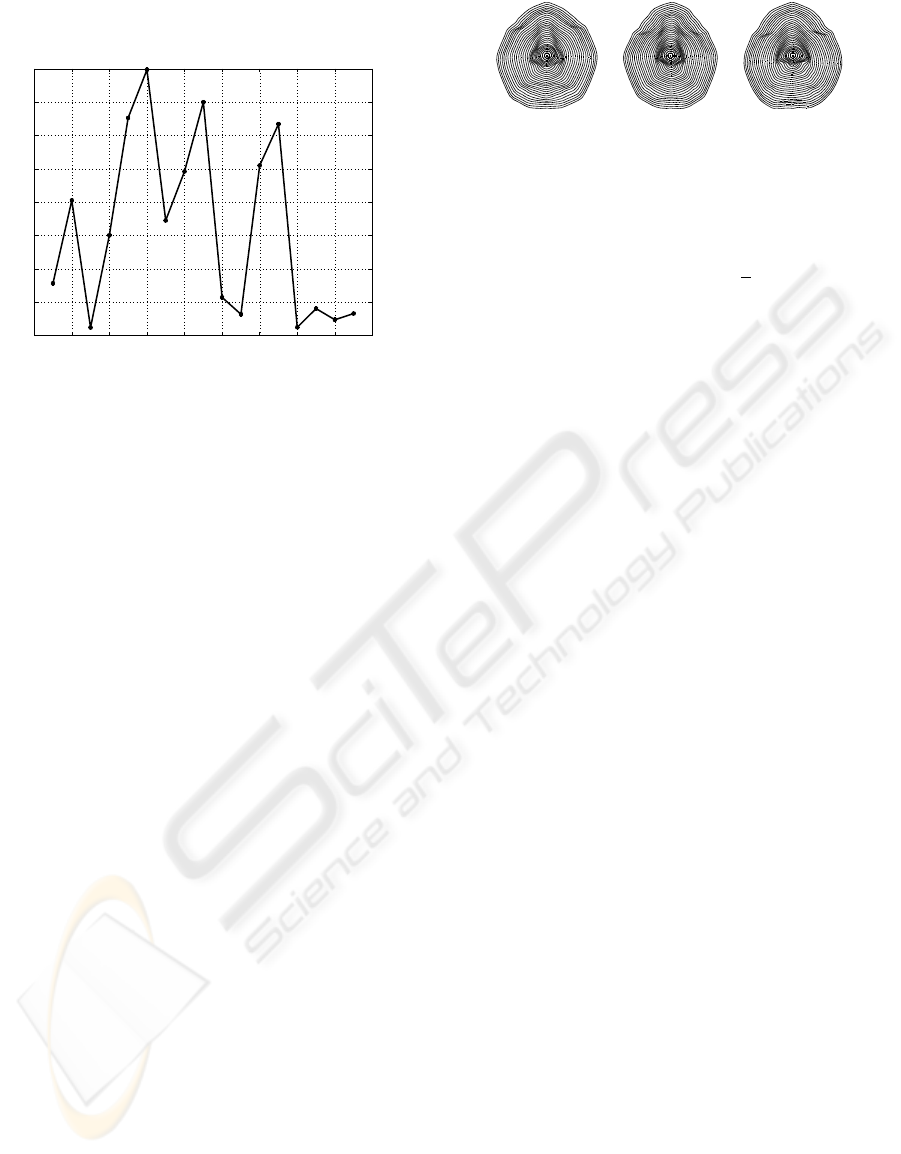
paths, ρ(β), provide the level of asymmetry of these

shapes. For the seventeen shapes shown in Figure 1,

the values of ρ(β) are shown in Figure 3. The bottle

and the fork are the most symmetric objects while the

fountain, the ﬂatﬁsh, the glass, and the tool are quite

close. On the other extreme, the cat and the chop-

per are the most asymmetric shapes. One can say that

the cat is almost ten times as asymmetric as the bot-

tle. To put these numbers in perspective, this measure

for the artiﬁcially constructed shape in the top right

ON ANALYZING SYMMETRY OF OBJECTS USING ELASTIC DEFORMATIONS

197

of Figure 2 is found to be 0.0814. This value can be

0 2 4 6 8 10 12 14 16 18

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Bone

bird

bottle

brick

camel

cat

car

carriage

chopper

crown

fountain

stef

rat

fork

tool

flatfish

Glas

Figure 3: The values of ρ(β) for the 17 shapes shown in

Figure 1.

treated as a numerical error in measuring symmetry of

perfectly symmetric objects. The last column shows

the optimal γs that resulted from optimal alignment

of curves with their reﬂections (Eqn. 5). For a per-

fectly symmetric shape γ is identity, while for largely

asymmetric shapes optimal γs are quite nonlinear.

4 SYMMETRY ANALYSIS OF

SURFACES

To analyze the symmetry of a surface is much more

complicated due to the corresponding difﬁculty in an-

alyzing shapes of surfaces. The space of parameteri-

zations of a surface is much larger than that of a curve,

and this hinders an analysis of symmetry in a way

that is invariant to parametrization. (Recall from pre-

vious sections that invariance to parametrization re-

quires solving an optimal re-parametrization of one

object, in order to best match the other.) One solu-

tion is to restrict to a family of parameterizations and

perform shape analysis over that space. Although this

can not be done for all surfaces, it is natural for cer-

tain surfaces such as the facial surfaces as described

next.

Using the approach of Samir et al., we can repre-

sent a facial surface S as an indexed collection of fa-

cial curves, as shown in Figure 4. Each facial curve,

denoted by c

, is obtained as a level set of the (sur-

face) distance function from the tip of the nose; it

is a closed curve in R

. The treatment of symme-

tries of closed curves in R

is similar to that of planar

curves described in the previous section. As earlier,

let d

denote the geodesic distance between closed

curves in R

, when computed on the shape space

S = C /(SO(3) ×Γ), where C is same as Eqn. 4 ex-

cept this time it is for curves in R

. A surface S is

Figure 4: Representation of facial surfaces as indexed col-

lection of closed curves in R

represented as a collection ∪

and the elastic dis-

tance between any two facial surfaces is given by:

) =

∑

(λ), where

(λ) = inf

O∈SO(3),γ∈Γ

γOq

(γ)) . (7)

Here q

and q

are q representations of the curves c

and c

, respectively. According to this equation, for

each pair of curves in S

and S

, c

and c

, we ob-

tain an optimal rotation and re-parametrization of the

second curve. To put together geodesic paths between

full facial surfaces, we need a single rotational align-

ment between them, not individually for each curve as

we have now. Thus we compute an average rotation:

O = average{O

} ,

using a standard approach, and apply

O to S

to align

it with S

. This global rotation, along with optimal

re-parameterizations for each λ, provides an optimal

alignment between individual facial curves and re-

sults in shortest geodesic paths between them. Com-

bining these geodesic paths, for all λs, one obtains

geodesic paths between the original facial surfaces.

We apply this idea for symmetry analysis of facial

surfaces. We take a surface S and form its reﬂection

in an arbitrary plane. Then, we extract facial curves

out of each surface and use these curves, as described

above, to form a geodesic path between the facial sur-

faces. Shown in Figure 5 is an example of a geodesic

path between a face, distorted by a smile, and its re-

ﬂection. For illustration, we show the geodesic using

both the rendered surfaces (top) and the facial curves

(bottom). In this case, the measure of asymmetry is

(S,

S) = 0.0210.

In Figure 6, we present some additional examples

of symmetrizing facial surfaces. From top to bottom,

the measure of asymmetry in these faces is 0.0217,

0.0147, 0.0156, and 0.0195.

5 SUMMARY

We have presented a framework for analyzing sym-

metries in 2D and 3D objects. This framework is

based on elastic deformations of objects in a fashion

that is invariant to rigid transformations and global

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

198

Figure 5: The geodesic path between a face and its reﬂection.

Figure 6: Examples of symmetry analysis of faces: geodesic between faces and their optimally aligned reﬂections.

scaling. The use of nonlinear registration techniques

help improve the quantiﬁcation of differences be-

tween shapes of objects and their reﬂections. This

framework provides a measure of asymmetry, the

nearest symmetric object, and a deformation ﬁeld for

symmetrizing an object.

ACKNOWLEDGEMENTS

This paper presents research results of the Belgian

Network DYSCO (Dynamical Systems, Control, and

Optimization), funded by the Interuniversity Attrac-

tion Poles Programme, initiated by the Belgian State,

Science Policy Ofﬁce. The scientiﬁc responsibility

rests with its author(s). This research was also sup-

ported in part by the ANR project under FAR3D

ANR-07-SESU-004, and CPER Nord-Pas de Calais

ambient intelligence.

REFERENCES

Joshi, S., Klassen, E., Srivastava, A., and Jermyn, I.

(2007a). A novel representation for riemannian anal-

ysis of elastic curves in R

. In CVPR.

Joshi, S., Klassen, E., Srivastava, A., and Jermyn, I.

(2007b). Removing shape-preserving transforma-

tions in square-root elastic (SRE) framework for shape

ON ANALYZING SYMMETRY OF OBJECTS USING ELASTIC DEFORMATIONS

199

analysis of curves. In Proc. of 6

EMMCVPR, Hubei,

China, pages 387–398.

Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2004).

Symmetry descriptors and 3D shape matching. In

Symposium on Geometry Processing.

Martinet, A., Soler, C., Holzschuch, N., and Sillion, F.

(2006). Accurate detection of symmetries in 3D

shapes. ACM Transactions on Graphics, 25(2):439

– 464.

Michor, P. W. and Mumford, D. (2006). Riemannian ge-

ometries on spaces of plane curves. Journal of the

European Mathematical Society, 8:1–48.

Mitra, N. J., Guibas, L., and Pauly, M. (2007). Symmetriza-

tion. In ACM Transactions on Graphics, volume 26,

pages 1–8.

Mitra, N. J., Guibas, L. J., and Pauly, M. (2006). Partial and

approximate symmetry detection for 3D geometry. In

ACM SIGGRAPH, pages 560–568.

Samir, C., Srivastava, A., and Daoudi, M. (2006). Three-

dimensional face recognition using shapes of facial

curves. IEEE Trans. Pattern Anal. Mach. Intell.,

28(11):1858–1863.

Simari, P., Kalogerakis, E., and Singh, K. (2006). Fold-

ing meshes: Hierarchical mesh segmentation based on

planar symmetry. In Eurographics Symposium on Ge-

ometry Processing 2006, pages 1824–1831.

Sun, C. and Sherrah, J. (1997). 3d symmetry detection

using the extended gaussian image. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

19(2):164–168.

Thrun, S. and Wegbreit, B. (2005). Shape from symmetry.

In ICCV ’05: Proceedings of the Tenth IEEE Interna-

tional Conference on Computer Vision, pages 1824–

1831, Washington, DC, USA. IEEE Computer Soci-

ety.

Tomaka, A. (2005). The application of 3d surfaces scanning

in the facial features analysis. Journal of Medical In-

formatics & Technologies, 9:233–240.

Zabrodsky, H., Peleg, S., and Avnir, D. (1995). Symmetry

as a continuous feature. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 17(12):1154–

1166.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

200