SELECTION OF MULTIPLE CLASSIFIERS WITH NO PRIOR
LIMIT TO THE NUMBER OF CLASSIFIERS BY MINIMIZING THE
CONDITIONAL ENTROPY
Hee-Joong Kang
Department of Computer Engineering, Hansung University, 389 Samseon-dong 3-ga, Seongbuk-gu, Seoul, Korea
Keywords:
Multiple classifier system, Multiple classifiers, Conditional entropy, Mutual information, Selection method.
Abstract:
In addition to a study on how to combine multiple classifiers in multiple classifier systems, recently a study
on how to select multiple classifiers from a classifier pool has been investigated, because the performance
of multiple classifier systems depends on the selected classifiers as well as a combination method. Previous
studies on the selection of multiple classifiers select a classifier set based on the assumption that the number of
selected classifiers is fixed in advance, or based on the clustering followed the diversity criteria of classifiers
in the classifier overproduce and choose paradigm. In this paper, by minimizing the conditional entropy which
is the upper bound of Bayes error rate, a new selection method is considered and devised with no prior limit
to the number of classifiers, as illustrated in examples.
1 INTRODUCTION
There have been a lot of studies to solve the pat-
tern recognition problems with a multiple classifier
system composed of multiple classifiers. The stud-
ies on a multiple classifier system have proceeded in
both directions of how to combine multiple classi-
fiers(Ho, 2002; Kang and Lee, 1999; Kittler et al.,
1998; Saerens and Fouss, 2004; Woods et al., 1997)
and how to select multiple classifiers from a classi-
fier pool(Ho, 2002; Kang, 2005; Roli and Giacinto,
2002), because the performance of a multiple classi-
fier system depends on the selected classifiers as well
as a combination method. It is well known that a set of
classifiers showing only high recognition rates is not
superior to other set of classifiers in most cases(Roli
and Giacinto, 2002; Woods et al., 1997), furthermore
it was also reported that fewer classifiers provided su-
perior results to more classifiers(Woods et al., 1997).
Thus, it is well recognized that the selection of com-
ponent classifiers in a multiple classifier system is
one of very difficult research issues(Ho, 2002; Kang,
2005; Roli and Giacinto, 2002; Woods et al., 1997).
Previous studies on the selection of multiple clas-
sifiers select a classifier set based on the assumption
that the number of selected classifiers is fixed in ad-
vance(Kang, 2005), or based on the clustering fol-
lowed the diversity criteria of classifiers in the over-
produce and choose paradigm without such assump-
tion(Roli and Giacinto, 2002). The selected classi-
fier set is used in a multiple classifier system and then
multiple classifiers in the set are combined for fusing
their classification results.
In this paper, in order to select multiple classifiers
in a systematic way, by minimizing the conditional
entropy which is the upper bound of Bayes error rate,
a new selection method is considered and devised
with no prior limit to the number of classifiers, as il-
lustrated in examples. The proposed selection method
is briefly compared to the previous selection methods.
2 RELATED WORKS
A preliminary study to select multiple classifiers was
conducted on the assumption that the number of se-
lected classifiers is fixed in advance. Under such
an assumption, classifiers are ordered according to
recognition rates or reliability rates, and then the clas-
sifiers are sequentially selected up to the fixed number
from the best one. And also, measure of closeness and
conditional entropy based on information theory were
applied to select a promising classifier set among clas-
sifier sets composed of the fixed number of classi-
fiers(Kang, 2005).
Based on the overproduce and choose paradigm
356
Kang H. (2009).
SELECTION OF MULTIPLE CLASSIFIERS WITH NO PRIOR LIMIT TO THE NUMBER OF CLASSIFIERS BY MINIMIZING THE CONDITIONAL
ENTROPY.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 356-361
DOI: 10.5220/0001799103560361
Copyright
c
 SciTePress

proposed by Partridge and Yates, a number of classi-
fiers are created, and then promising classifiers are se-
lected according to criteria(Roli and Giacinto, 2002).
In their selection, a heuristic function is used to select
the promising classifiers, or the best classifier is re-
spectively selected according to its category of clas-
sifiers, or the clustering followed the diversity crite-
ria of classifiers is applied to empirically decide the
number of classifiers complementary to each other.
Then, the selected classifiers are consisted of a clas-
sifier set in a multiple classifier system. By using the
clustering, a prior limit to the number of classifiers
is avoided and the number is decided. But, a classi-
fier set by the clustering can not guarantee the best
performance over others, so the number of selected
classifiers still remains an unresolved issue.
Various diversity criteria of classifiers are GD
(within-set generalization diversity) proposed by Par-
tridge and Yates, Q statistic proposed by Kuncheva et
al., CD (compound diversity) proposed by Roli and
Giacinto, and mutual information between classifiers
proposed by Kang(Kang, 2005; Roli and Giacinto,
2002). And additional diversity criteria of classifier
sets used in the clustering to decide the number of
classifiers are GDB (between-setgeneralization diver-
sity) proposed by Partridge and Yates, and diversity
function proposed by Roli and Giacinto(Roli and Gi-
acinto, 2002).
Q statistic criteria are expressed as follows.
Q
i, j
=
N
11
N
00
− N
01
N
10
N
11
N
00
+ N
01
N
10
(1)
Q
i, j,k
=
∑
a,b
Q
a,b
3
C
2
(2)
A diversity between two classifiers is calculated by
the Eq. 1, and a diversity among three classifiers is
calculated by the Eq. 2 which divides the sum of Q
statistic Q
a,b
for a pair of classifiers by the combina-
tion for a pair of classifiers. Here, N
11
is the num-
ber of data elements that both two classifiers cor-
rectly classify, and N
00
is the number of data elements
wrongly classified by both classifiers, and N
10
or N
01
is the number of data elements that either of classifiers
correctly classifies.
CD criterion is based on the compound error prob-
ability for two classifiers E
i
and E
j
and it is expressed
as follows when they are respectively the member of
each classifier set A and B.
CD(E
i
, E
j
) = 1− prob(E
i
fails, E
j
fails) (3)
diversity(A, B) = max
E
i
∈A,E
j
∈B
{CD(E
i
, E
j
)} (4)
3 SELECTION OF CLASSIFIERS
BASED ON THE
MINIMIZATION OF
CONDITIONAL ENTROPY
In a Bayesian approach to deal with pattern recogni-
tion problems using a multiple classifier system, the
upper bound of Bayes error rate P
e
is defined like
Eq. 5 by conditional entropy H(L|E) with a label
class L and a K classifiers group E. By minimizing
such conditional entropy, the upper bound of Bayes
error rate can be lowered and improvement on the per-
formance of a multiple classifier system can be ex-
pected. From the definition of conditional entropy,
class-decision (C-D) mutual information U(L;E) is
derived like Eq. 6. Lowering the upper bound of
Bayes error rate means maximizing the C-D mutual
information U(L;E).
C-D mutual information is also used to optimally
approximate high order probability distribution with
a product of low order probability distributions based
on the first-order or the second-order or the dth-order
dependency, when there are a high order probability
distribution P(E, L) composed of a class label L and
classifiers E, and a high order probability distribu-
tion P(E) composed of only classifiers. Below ex-
pressions show the derivation of finding the optimal
approximate probability distributions P
a
based on the
dth-order dependency from the C-D mutual informa-
tion.
P
e
≤
1
2
H(L|E) =
1
2
[H(L) −U(L;E)] (5)
U(L;E) =
∑
e
∑
l
P(e, l)log
P(e|l)
P(e)
=
∑
e
∑
l
P(e, l)log
∏
K
j=1
P(E
n
j
|E
n
id( j)
, ··· , E
n
i1( j)
, l)
P(l)
−
∑
e
P(e) log
K
∏
j=1
P(E
n
j
|E
n
id( j)
, ··· , E
n
i1( j)
)
= H(L) +
K
∑
j=1
∆D(E
n
j
;E
n
id( j)
, ··· , E
n
i1( j)
, L) (6)
P
a
(E
1
, ··· , E
K
, L) =
K
∏
j=1
P(E
n
j
|E
n
id( j)
, ··· , E
n
i1( j)
, L),
where(0 ≤ id( j), ·· · , i1( j) < j) (7)
P
a
(E
1
, ··· , E
K
) =
K
∏
j=1
P(E
n
j
|E
n
id( j)
, ··· , E
n
i1( j)
),
where(0 ≤ id( j), ·· · , i1( j) < j) (8)
H(L) = −
∑
l
P(l) logP(l) (9)
∆D(E
n
j
;E
n
id( j)
, ··· , E
n
i1( j)
, L) =
D(E
n
j
;E
n
id( j)
, ··· , E
n
i1( j)
, L) − D(E
n
j
;E
n
id( j)
, ··· , E
n
i1( j)
) (10)
SELECTION OF MULTIPLE CLASSIFIERS WITH NO PRIOR LIMIT TO THE NUMBER OF CLASSIFIERS BY
MINIMIZING THE CONDITIONAL ENTROPY
357

D(E
n
j
;E
n
id( j)
, ··· , E
n
i1( j)
, L) =
∑
e
∑
l
P(e, l)log
P(E
n
j
|E
n
id( j)
, ··· , E
n
i1( j)
, l)
P(E
n
j
)
(11)
D(E
n
j
;E
n
id( j)
, ··· , E
n
i1( j)
) =
∑
e
P(e) log
P(E
n
j
|E
n
id( j)
, ··· , E
n
i1( j)
)
P(E
n
j
)
(12)
P(E
n
j
|E
0
, E
0
, L) ≡ P(E
n
j
, L) (13)
P(E
n
j
|E
0
, E
n
i·( j)
, L) ≡ P(E
n
j
|E
n
i·( j)
, L) (14)
P(E
n
j
|E
0
, E
n
i·( j)
) ≡ P(E
n
j
, E
n
i·( j)
) (15)
From Eqs. 5 and 6, for a given set of K classifiers,
maximizing the C-D mutual information U() leads to
the decision of unknown permutation used in the op-
timal approximate probability distributions by maxi-
mizing the total sum of mutual information ∆D() like
Eq. 10 by the dth-order dependency. Eqs. 13 to 15 are
defined for confirming the property of probability and
E
0
is a null term. After deciding the unknown permu-
tation, an optimal product of low order distributions
can be found.
A selection method based on the conditional en-
tropy assumes that a classifier set having high C-D
mutual information is better than other classifier sets,
because the higher the C-D mutual information is the
lower the upper bound of Bayes error rate is. So, a
classifier set with the highest C-D mutual information
is selected as the classifier set of a multiple classifier
system. For example, for a classifier set composed
of one classifier E
1
, C-D mutual information is ex-
pressed as follows.
U(L;E
1
) =
∑
e
∑
l
P(e
1
, l)log
P(e
1
|l)
P(e
1
)
=
∑
e
∑
l
P(e
1
, l)log
P(e
1
, l)
P(l)
−
∑
e
P(e
1
)logP(e
1
)
= H(L) + H(E
1
) +
∑
e
∑
l
P(e
1
, l)logP(e
1
, l) (16)
And for a classifier set composed of two classifiers
E
1
, E
2
, C-D mutual information is expressed as fol-
lows.
U(L;E
1
, E
2
) =
∑
e
∑
l
P(e
1
, e
2
, l)log
P(e
1
, e
2
|l)
P(e
1
, e
2
)
=
∑
e
∑
l
P(e
1
, e
2
, l)log
P(e
1
, e
2
, l)
P(l)
−
∑
e
P(e
1
, e
2
)logP(e
1
, e
2
)
= H(L) + H(E
1
, E
2
)
+
∑
e
∑
l
P(e
1
, e
2
, l)logP(e
1
, e
2
, l) (17)
As mentioned above, for a classifier set composed of
K classifiers E
1
, ··· , E
K
, C-D mutual information is
expressed as follows without probability approxima-
tion.
U(L;E
1
, ··· , E
K
) =
∑
e
∑
l
P(e
1
, ··· , e
K
, l)log
P(e
1
, ··· , e
K
|l)
P(e
1
, ··· , e
K
)
=
∑
e
∑
l
P(e
1
, ··· , e
K
, l)log
P(e
1
, ··· , e
K
, l)
P(l)
−
∑
e
P(e
1
, ··· , e
K
)logP(e
1
, ··· , e
K
)
= H(L) + H(E
1
, ··· , E
K
)
+
∑
e
∑
l
P(e
1
, ··· , e
K
, l)logP(e
1
, ··· , e
K
, l)(18)
Therefore, possible classifier sets can be built by
increasing the number of classifiers to be added from
one, and then for a classifier set, when C-D mutual in-
formation U() can be computed, if there is no mean-
ingful increment on the C-D mutual information U(),
then adding a classifier to the classifier set is useless
because there is no lowering at the upper bound of
Bayes error rate. That is, no more classifiers addi-
ble is considered in building a classifier set. A classi-
fier set having the maximum C-D mutual information
is selected as the classifier set of a multiple classifier
system.
4 EXAMPLE OF MULTIPLE
CLASSIFIER SYSTEMS AND
ANALYSIS OF SELECTION
METHODS
In this section, four examples are shown to illus-
trate why multiple classifier systems are useful and
how a conditional entropy-based selection method af-
fects the performance of multiple classifier systems.
Five label classes are {A, B, C, D, E}, and then
let us suppose that training data and test data are
the same as the label classes. And also, it is sup-
posed that five imaginary classifiers are {Ea, Eb, Ec,
Ed, Ee}. Combination methods to combine classi-
fiers are voting method and conditional independence
assumption-based Bayesian (CIAB) method com-
monly used(Kang, 2005; Roli and Giacinto, 2002).
The first example, EX-1, supposes that five imag-
inary classifiers showing 20% recognition rate show
recognition results like Table 1 for the five test data.
In this example, classifier sets composed of one to five
classifiers are considered. Under these circumstances,
C-D mutual information computed by using Eqs. 16
to 18 are shown in Table 2. Additionally, Q statistic
is shown in column ’Q’ and CD diversity is shown in
column ’CD’. A plausible imaginary highest recog-
nition rate is denoted by ’pl’ in Table 3. The reason
why a classifier set composed of five classifiers can
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
358

have 100% pl rate assumes that a correct classifier is
rightly selected to decide its decision for each data.
For a classifier set composed of two classifiers, three
possible recognition rates in voting method is that the
recognitionrates depend on howto deal with tie votes.
This is the same situation as CIAB method.
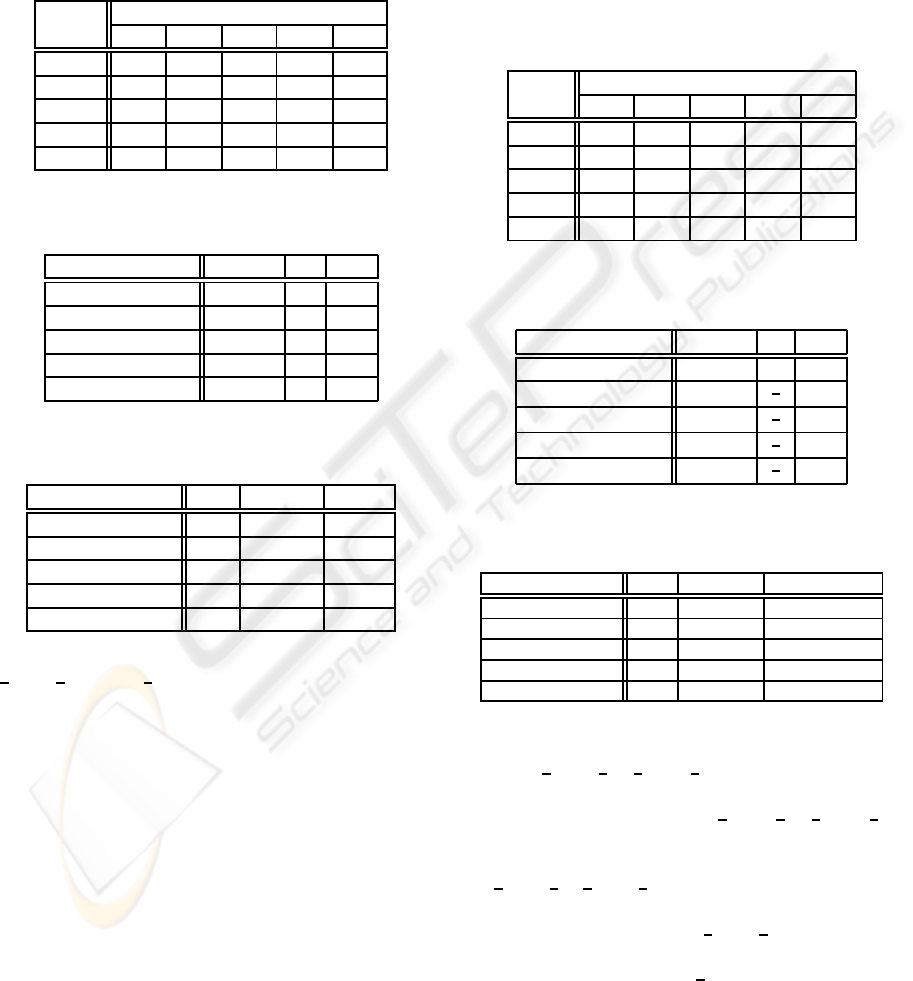
Table 1: Recognition result of EX-1 example.
classifier
data Ea Eb Ec Ed Ee
A A B C D E
B A B C D E
C A B C D E
D A B C D E
E A B C D E
Table 2: Diversity result of a classifier set of the EX-1 ex-
ample.
no. of classifiers U(L;E) Q CD
1 0 - -
2 0 -1 0.4
3 0 -1 0.4
4 0 -1 0.4
5 0 -1 0.4
Table 3: Recognition performance (%) of a classifier set of
the EX-1 example.
no. of classifiers pl voting CIAB
1 20 20 0,20
2 40 0,20,40 0,20
3 60 0 0,20
4 80 0 0,20
5 100 0 0,20
From the Table 2, U(L;E) is computed to 0 (e.g.,
1
5
∗ log
1
5
∗ 5 − log
1
5
= 0) regardless of the number of
classifiers in a classifier set by using the real proba-
bility distributions. And, Q statistic is -1 and CD is
0.4 in all cases except that the number of classifier is
one. Q and CD can not be computed when the num-
ber of classifier is one, so ’-’ means unavailable. For a
classifier set composed of more than three classifiers,
voting method shows 0% and CIAB method shows
at most 20% recognition rate. Although the above
example is simple and extreme, there is no positive
performance by the well representative combination
methods, voting and CIAB. If there is an oracle to se-
lect an appropriate classifier for a given input, then it
is possible to show 100% recognition rate as shown in
column ’pl’.
The second example, EX-2, supposes that five
imaginary classifiers showing 40% recognition rate
show recognition results like Table 4 for the five test
data. Classifier sets composed of one to fiveclassifiers
are considered. Under these circumstances, diversity
calculations are shown in Table 5 and performance
results are in Table 6. The reason why a classifier
set composed of four classifiers has 100% pl rate as-
sumes that 60% recognition rate is basic for the four
classifiers and for remaining rate a correct classifier is
rightly selected to decide its decision.
Table 4: Recognition result of EX-2 example.
classifier
data Ea Eb Ec Ed Ee
A A B C D A
B B B C D E
C A C C D E
D A B D D E
E A B C E E
Table 5: Diversity result of a classifier set of the EX-2 ex-
ample.
no. of classifiers U(L;E) Q CD
1 0.5004 - -
2 0.9503
1
3
0.6
3 1.3322
1
3
0.6
4 1.6094
1
3
0.6
5 1.6094
1
3
0.6
Table 6: Recognition performance (%) of a classifier set of
the EX-2 example.
no. of classifiers pl voting CIAB
1 40 40 40
2 60 20,40,60 40,60,80,100
3 80 40 60,80,100
4 100 60 100
5 100 100 100
From the Table 5, for a classifier set of one clas-
sifier, U(L;E) is approximately computed to 0.5004
(e.g., −(
4
5
∗ log
4
5
+
1
5
∗ log
1
5
) ≈ 0.5004), for a clas-
sifier set of two classifiers U(L;E) is approximately
computed to 0.9503 (e.g., −(
3
5
∗ log
3
5
+
1
5
∗ log
1
5
∗
2) ≈ 0.9503), for a classifier set of three classifiers
U(L;E) is approximately computed to 1.3322 (e.g.,
−(
2
5
∗ log
2
5
+
1
5
∗ log
1
5
∗ 3) ≈ 1.3322), and for a clas-
sifier set of four classifiers U(L;E) is approximately
computed to 1.6094 (e.g., −(
1
5
∗ log
1
5
∗ 5) ≈ 1.6094),
by using the real probability distributions from the
data. And, Q statistic is
1
3
and CD is 0.6 in all
cases except that the number of classifier is one. For
a classifier set composed of more than four classi-
fiers, while voting method shows 60%, CIAB method
SELECTION OF MULTIPLE CLASSIFIERS WITH NO PRIOR LIMIT TO THE NUMBER OF CLASSIFIERS BY
MINIMIZING THE CONDITIONAL ENTROPY
359

shows 100% recognition rate. Voting method is per-
fect with all five classifiers, but CIAB method is better
than voting method because the CIAB method is per-
fect with at least four classifiers. And, it is recognized
that C-D mutual information tends to show as similar
as the performance of CIAB method, but Q and CD
did not show any meaningful indication on the selec-
tion of classifiers. Therefore, when CIAB method is
used as the combination method of a multiple classi-
fier system, the number of classifiers can be decided
with reference to C-D mutual information of them,
and the number of selected classifiers is four.
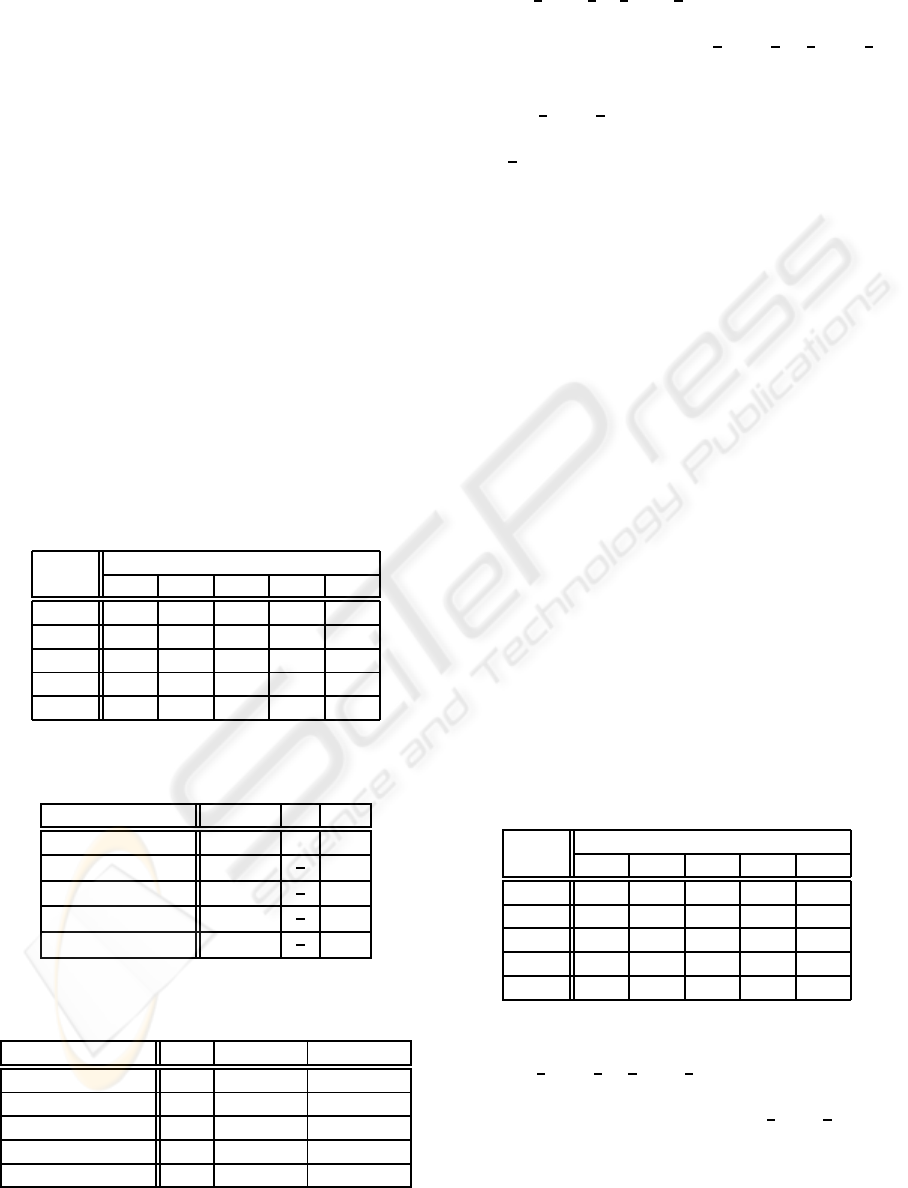
The third example, EX-3, supposes that five imag-
inary classifiers showing 60% recognition rate show
recognition results like Table 7 for the five test data.
Classifier sets composed of one to five classifiers are
considered. Under these circumstances, diversity cal-
culations are shown in Table 8 and performance re-
sults are in Table 9. The reason why a classifier set
composed of three classifiers has 100% pl rate as-
sumes that 60% recognition rate is basic for the three
classifiers and for remaining rate a correct classifier is
rightly selected to decide its decision.
Table 7: Recognition result of EX-3 example.
classifier
data Ea Eb Ec Ed Ee
A A B C A A
B B B C D B
C C C C D E
D A D D D E
E A B E E E
Table 8: Diversity result of a classifier set of the EX-3 ex-
ample.
no. of classifiers U(L;E) Q CD
1 0.9503 - -
2 1.3322
1
3
0.8
3 1.6094
1
3
0.8
4 1.6094
1
3
0.6
5 1.6094
1
3
0.6
Table 9: Recognition performance (%) of a classifier set of
the EX-3 example.
no. of classifiers pl voting CIAB
1 60 60 40,60
2 80 40,60,80 60,80,100
3 100 60 100
4 100 100 100
5 100 100 100
From the Table 8, for a classifier set of one clas-
sifier, U(L;E) is approximately computed to 0.9503
(e.g., −(
3
5
∗log
3
5
+
1
5
∗log
1
5
∗2) ≈ 0.9503), for a clas-
sifier set of two classifiers U(L;E) is approximately
computed to 1.3322 (e.g., −(
2
5
∗ log
2
5
+
1
5
∗ log
1
5
∗
3) ≈ 1.3322), and for a classifier set of three classi-
fiers U(L;E) is approximately computed to 1.6094
(e.g., −(
1
5
∗ log
1
5
∗ 5) ≈ 1.6094), by using the real
probability distributions from the data. And, Q statis-
tic is
1
3
and CD is 0.8 in all cases except that the num-
ber of classifier is one. For a classifier set composed
of more than three classifiers, while voting method
shows 60%, CIAB method shows 100% recognition
rate. Voting method is perfect with at least four clas-
sifiers, but CIAB method is better than voting method
because the CIAB method is perfect with at least three
classifiers. And, it is recognized that C-D mutual in-
formation tends to show as similar as the performance
of CIAB method, but Q and CD did not show any
meaningful indication on the selection of classifiers.
Therefore, when CIAB method is used as the com-
bination method of a multiple classifier system, the
number of classifiers can be decided with reference to
C-D mutual information of them, and the number of
selected classifiers is three.
The fourth example, EX-4, supposes that five
imaginary classifiers showing 80% recognition rate
show recognition results like Table 10 for the five test
data. Classifier sets composed of one to fiveclassifiers
are considered. Under these circumstances, diversity
calculations are shown in Table 11 and performance
results are in Table 12. The reason why a classifier
set composed of two classifiers has 100% pl rate as-
sumes that 60% recognition rate is basic for the two
classifiers and for remaining rate a correct classifier is
rightly selected to decide its decision.
Table 10: Recognition result of EX-4 example.
classifier
data Ea Eb Ec Ed Ee
A A B A A A
B B B C B B
C C C C D C
D D D D D E
E A E E E E
From the Table 11, for a classifier set of one clas-
sifier, U(L;E) is approximately computed to 1.3322
(e.g., −(
2
5
∗ log
2
5
+
1
5
∗ log
1
5
∗ 3) ≈ 1.3322), and for
a classifier set of two classifiers U(L;E) is approxi-
mately computed to 1.6094 (e.g., −(
1
5
∗ log
1
5
∗ 5) ≈
1.6094), by using the real probability distributions
from the data. And, Q statistic is -1 and CD is 1 in
all cases except that the number of classifier is one.
For a classifier set composed of more than two clas-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
360

Table 11: Diversity result of a classifier set of the EX-4
example.
no. of classifiers U(L;E) Q CD
1 1.3322 - -
2 1.6094 -1 1
3 1.6094 -1 1
4 1.6094 -1 1
5 1.6094 -1 1
Table 12: Recognition performance (%) of a classifier set of
the EX-4 example.
no. of classifiers pl voting CIAB
1 80 80 60,80
2 100 60,80,100 100
3 100 100 100
4 100 100 100
5 100 100 100
sifiers, while voting method shows three rates and at
most 100%, CIAB method shows 100% recognition
rate. Voting method is perfect with at least three clas-
sifiers, but CIAB method is better than voting method
because the CIAB method is perfect with at least two
classifiers. And, it is recognized that C-D mutual in-
formation tends to show as similar as the performance
of CIAB method, but Q and CD did not show any
meaningful indication on the selection of classifiers.
Therefore, when CIAB method is used as the com-
bination method of a multiple classifier system, the
number of classifiers can be decided with reference to
C-D mutual information of them, and the number of
selected classifiers is two.
5 DISCUSSION
The minimization of conditional entropy was previ-
ously applied to approximate the high order probabil-
ity distribution with the product of low order proba-
bility distributions, but in this paper it is tried to de-
cide the number of classifiers in a classifier set with
no prior limit and its promising usefulness was shown
in simple and obvious examples, by compared with
Q statistic and CD diversity. And also, in a classi-
fier set by the minimization of control entropy, CIAB
method is better than voting method. Even although
high order probability distribution was directly used
in computing the C-D mutual information without ap-
proximation in the simple examples, consideration on
the approximation of high order probability distribu-
tions will be needed because it is often hard to directly
obtain actual high order probability distributions. As
one of further works, the selection method proposed
in this paper will deeply be analyzed and compared
by previously proposed selection methods such as Q
statistic and CD diversity in other literature with a va-
riety of examples and real pattern recognition prob-
lems.
REFERENCES
Ho, T. K. (2002). Chapter 7 Multiple Classifier Combina-
tion: Lessons and Next Steps. In Bunke, H. and Kan-
del, A., editors, Hybrid Methods in Pattern Recogni-
tion, pages 171–198. World Scientific.
Kang, H.-J. (2005). Selection of Classifiers using
Information-Theoretic Criteria. Lecture Notes in
Computer Science, 3686:478–487.
Kang, H.-J. and Lee, S.-W. (1999). Combining Classifiers
based on Minimization of a Bayes Error Rate. In Proc.
of the 5th ICDAR, pages 398–401.
Kittler, J., Hatef, M., Duin, R. P. W., and Matas, J. (1998).
On Combining Classifiers. IEEE Trans. on Pattern
Analysis and Machine Intelligence, 20(3):226–239.
Roli, F. and Giacinto, G. (2002). Chapter 8 Design of Mul-
tiple Classifier Systems. In Bunke, H. and Kandel, A.,
editors, Hybrid Methods in Pattern Recognition, pages
199–226. World Scientific.
Saerens, M. and Fouss, F. (2004). Yet Another Method
for Combining Classifiers Outputs: A Maximum En-
tropy Approach. Lecture Notes in Computer Science,
3077:82–91.
Woods, K., Kegelmeyer Jr., W. P., and Bowyer, K. (1997).
Combinition of Multiple Classifiers Using Local Ac-
curacy Estimates. IEEE Trans. on Pattern Analysis
and Machine Intelligence, 19(4):405–410.
SELECTION OF MULTIPLE CLASSIFIERS WITH NO PRIOR LIMIT TO THE NUMBER OF CLASSIFIERS BY
MINIMIZING THE CONDITIONAL ENTROPY
361