
NEW CLOSED FORM SOLUTIONS FOR SKELETAL
EXTRACTION FROM MOTION CAPTURE
Jonathan Kip Knight
ITT, Colorado Springs, U.S.A.
Sudhanshhu Kumar Semwal
Departmemt of Computer Science, University of Colorado, Colorado Springs, U.S.A.
Keywords: Sphere-fit, Motion capture, Skeleton.
Abstract: We present a fast closed form solution for estimating the exact joint locations inside the human body from
motion capture data. The new closed-form solution is more robust and faster. For example, the formulae are
as much as about 100 times faster than the traditional non-linear Maximum Likelihood Estimator and about
9 times faster than linear least squares methods. The methods are proven to be statistically efficient when
measurement error is smaller than the joint-marker distance. Unbiased Generalized Delogne-Kása (UGDK),
multiple radii solution, and incremental GDK are important contributions of our research providing closed
form fast solutions for skeleton extraction from motion capture data. Skeletal animation sequences are
generated using the CMU and Eric Camper’s motion capture database.
1 INTRODUCTION
Skeleton extraction methods use temporal marker
positions from motion capture data to predict the
joint locations. These predicted joint locations then
define the skeleton. Recently, O’Brien et al., in 2000
(Brian, 2000) and with Kirk (Kirk, 2005) have
produced a fast method for skeleton extraction using
a linear least squares method assuming there is a
relatively stationary point between two segments,
and then solving for that point, which is essentially
the rotation point. Some years ago, Leendert de
Witte (Witte, 1960) found a solution for a circle in
3-D space. The Maximum Likelihood Estimator
(MLE) was the first solution for finding the sphere
parameters. In 1961 Stephen Robinson (Robinson,
1967) presented the iterative method of solving the
sphere and developed a closed form solution for the
radius estimator but not for the center estimator. In
1972, Delogne presented (Delogne, 1972) a method
for solving a circle for the purposes of determining
reflection measurements on transmission lines.
István Kása (Kasa, 1976) was the first to recognize
the bias in the answer and produced better error
analysis. Vaughan Pratt (Pratt, 1987) produced a
very generic linear least squares method for
algebraic surfaces. Gander (Gander, 1994) produced
the linear least-squares method for circle fitting.
Samuel Thomas (Thomas, 1995) created a formula
for the Cramér-Rao Lower Bound for the circle
estimation. Lukács (Lukas, 1997) produced some
improvements on non-linear minimization for
spheres. Corral et al. (Corral, 1998) analyzed Kása’s
formula in more detail and a way to reject the
answer if the confinement angle got too small.
Strandlie et al. (Strandlie, 2000) transformed a
Riemann sphere into a plane and fit the plane using
standard methods involving the eigenvalues of the
sample covariance matrix. Zelniker (Zelnicar, 2003)
reformulated the circle equation to solve directly for
the center using the pseudo-inverse (
#
) of a 2xN
matrix. Michael Burr et al. (Burr, 2004) created a
geometric inversion technique which far surpassed
the complexity needed to solve for a hypersphere.
Knight et al. (Knight, 2007) published the initial
results from the research for this dissertation in
which a skeleton was formed from a closed-form
solution of generic motion capture data.
249
Semwal S. and Knight J.
NEW CLOSED FORM SOLUTIONS FOR SKELETAL EXTRACTION FROM MOTION CAPTURE.
DOI: 10.5220/0001799702490256
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications (VISIGRAPP 2009), page
ISBN: 978-989-8111-67-8
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 SKELETAL EXTRACTION
Producing a skeleton involves finding the centers of
joint rotations, the hierarchy of segmentation, and
the orientation of each segment. The hierarchy of
segmentation is known ahead of time such as in
human animation. The orientation of a segment is
determined by one of two methods. Either it is given
in the raw data, e.g. magnetic trackers, or it is
calculated by the fastest technique known. One of
the earliest uses found in motion capture were
published by Herda et al. (Herada, 2000). The most
common approach to calculating a skeleton from
motion capture data is through minimization until
the skeleton fits where the rotation points have been
approximated. The minimization involves squishing
segments and moving joints until all joints are
nearest to the calculated rotation points. O’Brien et
al. (O’Brian, 2000) uses a linear least-squares
minimization that produces the rotation points from
a collection of time frames. In their study, magnetic
motion tracking devices are used which contain both
position and orientation. This is akin to solving for
the best-fit sphere around a center. 3D marker
trajectories are also analyzed in (de-Aguiar, 2006).
In the following section, we start with
explanation of symbols and conventions. In Section
4, we visit some methods which have been used in
various techniques as a prelude to generalized
Generalized Delogne-Kása (GDK) method in
Section 5 which include three contributions of our
paper – unbiased GDK (Section 6), multiple radii
solution (Section 7), and incremental GDK (Section
8). A comparison of all techniques is in Section 10
along with further research (Section 11).
Figure 1: Skeleton from motion capture data.
3 SYMBOLS
Oy
(
)
-- on the order of (i.e. size of) y
N
-- number of measurements
CRLB
-- Cramér-Rao Lower Bound covariance of
estimator
D -- dimension of hypersphere
FLOP
-- floating point operation
x
i
--- i
th
measurement of position
x
--- average of all measurements of positions
μ
i
--- expectation of the i
th
position
μ
--- average of expectations of all positions
Σ
-- measurement covariance of each position
ˆ
Σ
-- measurement covariance estimator
σ
-- measurement standard deviation
C -- sample covariance
C
0
-- true covariance of expected positions
S -- sample third central vector moment
S
0
-- true third central moment of expected positions
0
F -- true 4th central moment of expected positions
ˆ
c
--- center estimator
c
0
-- true center of hypersphere
ˆ
r
-- radius estimator
r
0
-- true radius of hypersphere
λ
-- eigenvalue of matrix
v -- eigenvector of matrix
x
T
-- transpose of column vector into row vector
A
−
1
-- multiplicative inverse of matrix
A
T
-- transpose of matrix
∇
-- vector gradient operator
x
-- magnitude of vector
A
-- determinant of matrix
N
3
μ
,
Σ
(
)
-- 3D vector Normal Distribution
ρ
A
(
)
-- spectral radius of matrix
Tr A
(
)
-- trace (sum of diagonals) of matrix
EA
(
)
-- expectation of random variate
Var A
(
)
-- variance of random variate
Cov A,B
(
)
-- covariance of two variates
4 SPHERICAL CURVE FITTING
APPROACHES
There are three techniques in use today: iterative;
least squares; and algebraic best fits. They each have
their advantages and disadvantages. Iterative
techniques are good for accuracy, least squares are
faster than iterative but slower than algebraic, and
algebraic techniques are good for speed.
4.1 Monte-Carlo Experiments
In order to compare the methods, a Monte-Carlo
experiment was run using 1000 trials, each of which
had anywhere from 4 to 1,000,000 samples. The
runs took over a week of computational effort to
collect. Each trial had a fixed standard deviation of
the samples from the sphere with values ranging
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
250
from 10
-13
to 10
14
. The sample must be confined to
be within an angle from a fixed point on the sphere.
This experiment allows for the in-depth analysis of
the error in the answer from four different
estimators. The four techniques are Maximum-
Likelihood Estimator (MLE) (Section 4.3), Linear
Least-Squares (LLS) (Section 4.4), Generalized
Delogne-Kása Estimator (GDKE) (Section 5), and
the new Unbiased Generalized Delogne-Kása
estimator (UGDK) explained in Section 6. The first
three are established formulae and has been used for
two hundred years (MLE (Shakarji, 1998)) to as
young as three years (GDKE (Zelnicker, 2003)).
UGDK is new method proposed in this paper. The
following graph (Figure 2) shows the errors in the
estimators compared to the standard deviation of the
samples indicating that UGDK performs closest to
CRLB. The graph shows that the relative error
versus relative standard deviation is a line for each
of these methods. The error is thus proportional to
the standard deviation on a log-log display showing
a power law. What is also clear from the graph is the
comparison. The outliers on the graph have been
circled. The obvious differences between the
estimators show up in the graph by deviations from
the straight line when error equals standard
deviation. From the graph, it appears that there is a
common limitation to the error in the estimator. This
common limitation is named the Cramér-Rao Lower
Bound to the covariance of an estimator. The
following sections discuss the limit to all estimators
for this particular problem. The MLE has outliers
when the error equals the radius. This is due to
multiple solutions when the error equals the radius.
The LLS has outliers when the standard deviation is
below about 10
-6
times the radius and greater than
10
10
times the radius. These are due to numerical
instability during the extremes of using finite
representation of decimal numbers. The GDKE
seems to be on par with the MLE except for the
MLE outliers. The UGDK is consistently close to
the CRLB indicating that it is more accurate than
other methods.
Error of Center Estimate
1E-17
1E-15
1E-13
1E-11
0.000000001
0.0000001
0.00001
0.001
0.1
10
1000
100000
10000000
1000000000
1E+11
1E+13
1E+15
1E+17
1E-14 1E-10 0.000001 0.01 100 1000000 1E+10 1E+14
MLE
LLS
GDKE
UGDK
CRLB
Figure 2: Shows relative error comparison.
4.2 Cramér-Rao Lower Bound (CRLB)
The Cramér-Rao Lower Bound (CRLB) is the
proven lower bound for any estimator’s covariance.
It is equal to the inverse of the Fisher Information. It
is an important measure when dealing with any
estimator because it is the best error that an
estimator can achieve. All estimators will have at
best an error of the CRLB.
4.3 Non-linear Maximum Likelihood
Estimator (MLE)
According to the National Institute of Standards and
Technology (NIST) (Shakarji, 1998) the best way to
find the center of a sphere is through non-linear
minimization of the variance of the radius. This is
also called the Maximum-Likelihood Estimator
(MLE) for the center
ˆ
c
and radius
ˆ
r
. The
minimization is usually carried out by iterative
methods like the Levenberg-Marquardt Method
(Shakarji, 1998) and cannot be solved directly.
4.4 Linear Least Square Method (LLS)
The next best thing to the very slow MLE method is
through linear least-squares solution. This is usually
an over-constrained problem since there are N
equations and four (i.e. D+1) unknowns. The N
equations can be put into a single matrix equation to
solve with standard linear algebra techniques. When
LLS and CRLB are compared, once again, the
outlier cases show that the answer erroneously lies
on the sphere. For the most part, the answer error is
proportional to the square root of the CRLB. The
next fastest algorithm is the linear least squares
method which has been analyzed in floating point
operations (FLOPS) in (Knight, 2008) with D=3 as
FLOPs 3
(
)
= N236 + 709
An estimator of a parameter is considered biased
if it is expected to be a little off of the real answer.
Zelniker (Zelnicker, 2003) has shown that the bias of
the GDKE is on the order of the measurement
standard deviation. Our statistical analysis has
shown that there are cases when the bias is quite
significant and does not disappear even when more
samples are taken. The dashed bar in Figure 3 show
that the true center is not anywhere within the error
ellipsoid of the estimate. This is due solely to the
bias in the estimator. This is a good example of why
the GDKE has not been adopted as much as the
others.
NEW CLOSED FORM SOLUTIONS FOR SKELETAL EXTRACTION FROM MOTION CAPTURE
251

Figure 3: GDKE error ellipse.
5 GENERALIZED
DELOGNE-KASA EXPOSITION
The Generalized Delogne-Kása (GDK) estimator
(Strandlie, 2000) is the starting basis for our new
formulae. This estimator is a general solution for
finding the best-fit hypersphere from measurements
on the surface. However until now the estimator has
limited uses as the estimator is biased and can
produce significantly different answers from the
solution. The GDK estimator provides a good
estimate if the data is evenly distributed over the
entire surface of the hypersphere. The estimate falls
farther away as the data gets clumped to one side.
The GDK estimator is derived from surface
measurements x
i
and their deviation from a fixed
distance from the center. The deviation for N
measurements is written as
s
GDK
2
ˆ
c,
ˆ
r
()
=
1
N −1
x
i
−
ˆ
c
()
T
x
i
−
ˆ
c
()
−
ˆ
r
2
()
2
i=1
N
∑
(1)
The minimization of this (Knight, 2008)
produces estimations for the center and the radius
ˆ
c =
x +
1
2
C
−1
S
(2)
ˆ
r
2
=
1
N
x
i
−
ˆ
c
()
T
x
i
−
ˆ
c
()
i=1
N
∑
(3)
where the intermediate quantities include the
arithmetic vector mean
x =
1
N
x
i
i=1
N
∑
(4)
and the variance-covariance matrix
C =
1
N−1
x
i
− x
()
x
i
− x
()
T
i=1
N
∑
(5)
and the third central vector moment
S =
1
N−1
x
i
− x
()
x
i
− x
()
T
x
i
− x
()
i=1
N
∑
(6)
This estimation of the hypersphere is very fast
due to the Cholesky inverse. The floating point
operations for a D-dimensional hypersphere can be
counted as
FLOPs = ND
2
+ 6 D − 1
(
)
+
1
3
DD+ 1
()
D + 8
()
+ 1
(7)
which, for the sphere, is
F
LOPs
=
N
26
+
45
(8)
This estimator is about as fast as you can get for
this problem but it has one fatal flaw. The estimator
has been shown to be biased providing an answer
that is offset even under fairly normal conditions.
The bias is proportional to the variance of the data
(Zelniker, 2004) but analysis here shows the
multiplication factor can outweigh an accurate
measurement. The bias comes from the fact that one
of the variables in the center equation is biased. We
consider a measurement system that has a consistent
error for each measurement on the surface of the
sphere. The measurement is expected to be on the
surface but varies from it by the multi-dimensional
Gaussian distribution thus
x
i
= Gaussian
D
μ
i
, Σ
(
)
(9)
The covariance matrix is then expected to be
E C
(
)
=
C
0
+
Σ
(10)
C
0
=
1
N−1
μ
i
−
μ
()
μ
i
−
μ
()
T
i
=
1
N
∑
(11)
E S
(
)
=
S
0
(12)
S
0
=
1
N−1
μ
i
−
μ
()
μ
i
−
μ
()
T
μ
i
−
μ
()
i
=
1
N
∑
(13)
E
ˆ
c
()
= c
0
+
1
2
C
0
+Σ
()
−1
− C
0
−1
(
)
S
0
+L
(14)
6 UNBIASED GDK
Unbiased GDK provides a quick method to draw a
skeleton from motion capture data. The main
contribution to the state of the art is that the
estimator explained below is asymptotically
unbiased. Asymptotically unbiased is defined as an
inversely proportional relationship with the sample
count:
E
ˆ
q
(
)
=
q
0
+
O
1
N
(
)
where q
0
is the parameter
that the estimator is trying to estimate. This basically
says that the estimator is expected to get closer to
the true answer if more samples are taken. It is
shown in (Knight, 2008) that the GDKE estimators
for center and radius do not satisfy this requirement.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
252

Our algorithm uses a simple substitution that turns
the GDKE into one with a diminishing bias. It
involves the use of an a-priori estimate of the
measurement error in the samples. This is very
reasonable since most systems of measurement have
some kind of estimate to the measurement error.
Since the sample covariance matrix C is the only
biased term in the equation for the GDKE center,
this is what will be altered.
′
C = C−
ˆ
Σ
(15)
E C −
ˆ
Σ
()
= C
0
+Σ−
ˆ
Σ
(16)
ˆ
c
u
= x +
1
2
C −
ˆ
Σ
()
−1
S
(17)
ˆ
r
u
=
N −1
N
Tr C −
ˆ
Σ
()
+ x −
ˆ
c
u
()
T
x −
ˆ
c
u
()
(18)
Tr
ˆ
Σ
()
=
1
N
x
i
− c
0
()
T
x
i
− c
0
()
i=1
N
∑
− r
0
2
(19)
This leads to fastest, asymptotically unbiased
estimator of a hypersphere in (Knight, 2008) as
ˆ
′
c =
x +
1
2
C−
ˆ
Σ
()
−1
S
(20)
ˆ
′
r =
N−1
N
Tr C−
ˆ
Σ
()
+ x −
ˆ
′
c
()
T
x −
ˆ
′
c
()
(21)
A typical use of these new estimators can be
displayed using Mathematica, with exactly the same
data as used for displayed for the GDKE. The true
center is within the error ellipsoid (Figure 4). This
data contains 100 points generated with a diagonal
measurement covariance with all diagonals equal to
0.05
2
. The Leontief condition (
ρ
<1
) is satisfied with
the spectral radius in question equal to 0.557238.
These equations show that there still is a bias, but it
is asymptotically unbiased. We implemented (results
in Figure 4). A Monte-Carlo run that explicitly
shows the 1/√N dependency. The error in the
estimate is compared with how many points were
analyzed for a particular joint in given motion
capture data.
Figure 4: UGDK error ellipse.
An example analysis using MLE, UGDK and
GDKE is presented in Figure 5. The figure clearly
shows the improvement over the GDKE with same
FLOP count for UGDK as GDKE. The figure shows
the bias is removed using the UGDK and results
produced by UGDK are close to MLE. The FLOP
counts for UGDK remains same as GDK (Knight
2008). Our analysis in (Knight 2008) also shows that
there is a case when all methods have troubles in
estimating the joint location – this is the case when
measurement error is actually bigger than the item
being measured. This situation is a bit impractical,
as no one wants such a system of measurement.
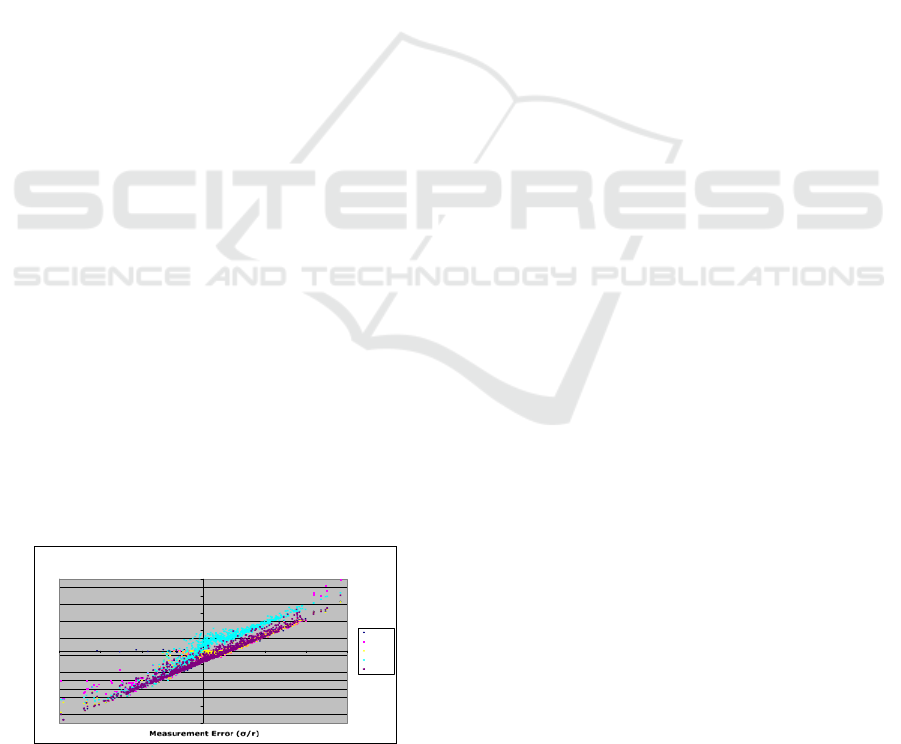
Figure 5: Comparison of methods.
7 NEW SOLUTION: MULTIPLE
RADII SOLUTION
For multiple markers going around the same center
of rotation, another formula can be achieved by the
same analysis of least squares. This technique is
good to use when more than one marker is available.
It has the ability to average out errors when one
marker is too close to the rotation point or has other
systematic problems. Excluding the derivation, we
have the following equations for center and radius
estimates where M is the number of markers and
subscript p indicates values that utilize the single
marker’s positions:
ˆ
c
m
= C
p
−
ˆ
Σ
()
p=1
M
∑
⎛
⎝
⎜
⎞
⎠
⎟
−1
C
p
−
ˆ
Σ
()
x
p
+
1
2
S
p
p=1
M
∑
(22)
ˆ
r
p
=
N −1
N
Tr C
p
−
ˆ
Σ
(
)
+ x
p
−
ˆ
c
m
()
T
x
p
−
ˆ
c
m
()
(23)
Symbols and conventions are given in Section 2.
The matrix that is to be inversed here is still a
positive-definite matrix since positive-definite
matrices added together still produce a positive-
definite matrix. This allows for the speedier
Cholesky decomposition and the singular values can
be excluded. An example of the MGDK method is
presented in Figure 6. This example shows what
happens when the individual circles are compared to
that when combined in the MGDK. The outer circle
solution is drawn in red; the inner circle solution is
drawn in blue, and the MGDK solution is drawn in
green. The example shows a dramatic improvement
over both of the individual circle calculations. FLOP
count analysis is in (Knight, 2008).
NEW CLOSED FORM SOLUTIONS FOR SKELETAL EXTRACTION FROM MOTION CAPTURE
253

Figure 6: Comparison of methods.
8 NEW SOLUTION: IGDK
A more refined answer can be achieved when using
a incremental improvement GDK (IGDK) formula.
The idea here is a group of samples are collected and
an answer is retrieved from the GDKE or UGDK
formulae. Excluding the derivation, we have the
following equations. Equations for S and C for
(n+1)th sample are defined in (Knight, 2008) and are
calculated using recurrence relationship. Below are
the final equations for the center and radius. The
advantage is that no new matrix inverse is needed
and the storage requirements are of constant order.
ˆ
c
n+1
= x
n+1
+
1
2
C
n+1
−1
S
n+1
(24)
ˆ
r
n+1
2
=
n
n+1
Tr C
n+1
()
+ x
n+1
−
ˆ
c
n+1
()
T
x
n+1
−
ˆ
c
n+1
()
(25)
When compared to the FLOPs for the GDKE
method, this incremental approach is about four
times slower. This makes the incremental approach a
last resort when a few extra points need to be added
to a previously calculated center and radius. This
new estimator has the distinct advantage of constant
memory requirements no matter how many points
are analyzed.
9 EXPERIMENTS
9.1 Case Study – CMU Data
The CMU Graphics Lab produced a one minute long
motion capture data-set of a salsa dance in 60-08.
The data file contains 3421 time slices for 41
markers on two figures. This case study will
concentrate on analyzing the performance of the
UGDK in determining the rotation points in the
female subject. Four data sets were created by
removing random samples from the CMU data sets.
400 rotation points were collected. The calculated
constants are the relative rotation points as
referenced in each segment’s parent’s coordinate
system. The 400 calculations were averaged and the
standard deviations were calculated as well. Details
results are analyzed in (Knight, 2008) Most of the
standard deviations are less than one centimeter, but
there are some significant outliers like the right
ankle. Further analysis of the calculated points for
the ankles and elbows shows that the four runs
produced two answers due to different orientations
of the parent’s reference frame. As can be readily
seen from the above graph, a statistically significant
amount of calculations are within one centimeter of
accuracy when analyzing more than about 200
samples. The accuracy gets better on average with a
power law close to 1/√N (Figure 7). Skeletal
animation of our results is provided in mpeg files.
Deviation From Mean Rotation Point
y = 0.5117x
-0.8125
0.00001
0.0001
0.001
0.01
0.1
1
0 500 1000 1500 2000 2500 3000 3500
Number of Samples
Figure 7: Inverse Power Law.
9.2 Case Study of Eric Camper’s
ACCAD Data
The motion capture data in the ericcamper.c3d
(Motion was analyzed to produce a skeleton. The
subject did various martial arts maneuvers that
moved every joint involved in drawing. One time
frame is presented in the following figure. We show
a frame of animation in Figure 1 which shows what
appears to be a natural pose for all joints during a
karate exercise.
10 RESULTS
A Monte-Carlo experiment was set up to determine
the speed of the various sphere-fit algorithms. Up to
a million samples were chosen on a sphere with
varying measurement error, confinement angle,
sphere-center and sphere-radius. The measurement
error varied from 1x10
-11
to 1x10
12
. The confinement
angle varied from 0 to 180°. The sphere center
varied as much as 2 around the origin. The radius
varied 0 to 37. The linear algebra algorithms were
all implemented from well-accepted
implementations presented in Numerical Recipes in
C (Press, 1992) The code was compiled optimized
for a PowerPC G4 processor and run on a 1GHz
Apple PowerBook 12”.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
254

As discussed in (Knight, 2008), the GDKE, and
therefore UGDK, is always faster with FLOP count
as 26 N. The GDKE/UGDK is 2.17 times faster than
IGDK on average. Based on FLOP counts as
explained in (Knight, 2008) in detail, the
GDKE/UGDK is 11.05 times faster than the LLS
method and about 80 times faster than the MLE
when the measurement error is less than one.
10.1 Summary of Important Results
Three new closed-form methods have been
presented to find rotation points of a skeleton from
motion capture data. A generic skeleton can be
directly extracted from noisy data with no previous
knowledge of skeleton measurements. The new
methods are ten times faster than the next fastest and
a hundred times faster than the most widely accepted
method. Two phases are used to produce an accurate
skeleton of the captured data. The first phase, fitting
the skeleton, is robust even with noisy motion
capture data. As explained earlier, the formulae use
an asymptotically unbiased version of the
Generalized Delogne-Kása (GDKE) Hyperspherical
Estimation (i.e UGDK). The second estimator takes
advantage of multiple markers located at different
distances from the rotation point (MGDK) thereby
increasing accuracy. The third estimator
incrementally improves an answer and has
advantages of constant memory requirements
suitable for firmware applications (IGDK). The
UGDK produces the answer faster than any previous
algorithm and with the same efficiency with respect
to the Cramér-Rao Lower Bound for fitting spheres
and circles. The UGDK method significantly
reduces the amount of work needed for calculating
rotation points by only requiring 26N flops for each
joint. The next fastest method, Linear Least-Squares
requires 236N flops. In-depth statistical analysis
shows the UGDK method converges to the actual
rotation point with an error of O(σ/√N) improving
on the GDKE’s biased answer of O(σ). The second
phase is a real-time algorithm to draw the skeleton at
each time frame with as little as one point on a
segment. This speedy method, on the order of the
number of segments, aids the realism of motion data
animation by allowing for the subtle nuances of each
time frame to be displayed. Flexibility of motion is
displayed in detail as the figure follows the captured
motion more closely. With the reduced time
complexity, multiple figures, even crowds can be
animated. In addition, calculations can be reused for
the same actor and marker-set allowing different
data sets to be blended.
11 CONCLUSIONS
In our effort to try to speed up skeleton extraction
from motion capture date we discovered a new
asymptotically unbiased GDK (UGDK) formulation
which fills the vital low-level hole and makes GDK
formulation practical. This paper presents the fastest
known general method for calculating the rotation
points and can be as much as ten times faster than
the next fastest method available as explained in
(Knight, 2009) The UGDK method has further
impact in a vast collection of fields as diverse as
character recognition to nuclear physics where an
algorithm is needed for the speedy recovery of the
center of a circle or sphere. The UGDK is expected
to play a vital role in the process of determining a
skeleton from motion capture data. The MGDK adds
robustness to the equations allowing to use every bit
of available data. The IGDK further has the
application of being an ideal algorithm to burn into a
silicon chip whose memory requirements are
constrained.
The UGDK estimators are an improvement on
existing science but they are strictly dependent on a-
priori knowledge of the measurement error. It has
been shown that the measurement error trace can
itself be estimated but not the whole measurement
covariance matrix. An estimator for the whole
matrix would be most ideal but was not found in the
course of this study and should be a topic of future
research. The main contributions are the new
unbiased center formulae; the full statistical analysis
of this new formula; and the analysis of when the
best measurement conditions are to initiate the
formula. The research further establishes the
application of these new formulae to motion capture
to produce a real-time method of drawing skeletons
of arbitrary articulated figures. is advisable to keep
all the given values.
Figure 8: A sample of File menu interface.
NEW CLOSED FORM SOLUTIONS FOR SKELETAL EXTRACTION FROM MOTION CAPTURE
255

ACKNOWLEDGEMENTS
We wish to thank all the reviewers of the paper,
especially numbers 3 and 4, for their insightful
comments.
REFERENCES
Aguiar, D., Theobalt, C., Seidal,H., Automatic learning of
articulated Skeletons from 3D marker Trajectories, in
International Symposium, ISVC 2006, part I, Springer-
Veralag, Lecture Notes in Computer Science, vol.
4291, pp. 485-494 (2006).
O’Brien, J. F., Bodenheimer Jr R. E. ., Brostow G. J., and
Hodgins J. K..
Automatic Joint Parameter Estimation
from Magnetic Motion Capture Data
, pages 53–60,
Montreal, Quebec, Canada, May 15-17 2000. Graphics
Interface.
Burr, M., Cheng, A., Coleman, R., and Souvaine, D.,
Transformations and Algorithms for Least Sum of
Squares Hypersphere Fitting.
16
th
Canadian
Conference on Computational Geometry,
2004, pp
104-107.
Camper, E., Motion Capture Data accaccad.osu.edu/
research/mocap/mocap_research.html
Corral, C., Lindquist, C., On implementing Kása’s circle
fit procedure.
IEEE Transactions on Instrumentation
and Measurement
, 47(3):789–795, June 1998.
Delogne, P.,Computer Optimization of Deschamps
Method and Error Cancellation in Reflectometry. In
Proceedings of the IMEKO Symposium on Microwave
Measurements
, Budapest, Hungary, May 1972, pp.
117-129.
Gander, W., Golub, G., Strebel, R., Least-Squares Fitting
of Circles and Ellipses.
BIT Numerical Mathematics
34, Springer 1994, pp 558-578.
Herda, L., Fua, P., Plankers, R., Boulic, R., D. Thalmann,
D., Skeleton-based motion capture for robust
reconstruction of Human Motion, Computer
Animation (book), Philadelphia, PA, pp.77-May
(2000).
Kása, I., A circle fitting procedure and its error analysis.
IEEE Transactions on Instrumentation and
Measurement
, 25:8–14, March 1976.
Kirk, A. G., O’Brien, J., Forsyth, D.A. Skeletal parameter
estimation from optical motion capture data. In
IEEE
Conf. on Computer Vision and Pattern Recognition
(CVPR). IEEE, 2005.
Knight, J., Semwal, S., Fast Skeleton estimation from
motion captured using Genralized Delogne-Kasa
method, In
15
th
International Conference in Central
Europe on Computer Graphics, Visualization and
Computer Vision, Plzen, WSCG Conference
Proceedings, pp. 225-232, ISBN 978-80-86943-98-5,
Feb 2007.
Knight, J., Rotation Points from Motion Capture Data
using a closed form solution,
PhD thesis, University of
Colorado at Colorado Springs, Advisor Professor
Semwal, SK., pp. 1-152 (2008).
Lukács, G., Marshall, A., Martin, R., Geometric Least-
Squares Fitting of Spheres, Cylinders, Cones, and Tori
RECCAD Deliverable Documents 2 and 3 Copernicus
Project No. 1068
Reports on basic geometry and
geometric model creation, etc. Edited by Dr. R. R.
Martin and Dr. T. Varady Report GML 1997/5,
Computer and Automation Institute, Hungarian
Academy of Sciences, Budapest, 1997.
Pratt, V., Direct least-squares fitting of algebraic surfaces.
Computer Graphics, 21(4):145–152, July 1987.
Press, W., Teukolsky, T., Vetterling, W., Flannery, B.,
Numerical Recipes in C: The Art of Scientific
Computing. 2nd.ed., Cambridge University Press:
1992.
Robinson, S.Fitting Spheres by the Method of Least
Squares,
In Communications of the ACM, Volume 4,
No. 11; November 1967, p. 491.
Shakarji, C., Least-Squares Fitting Algorithms of the
NIST Algorithm Testing System,
J. of Research of the
National Institute of Standards and Technology
: 103,
No. 6 (1998): 633.
Strandlie, A., Wroldsen, J., Frühwirth, R., and
Lillekjendlie, B.,Track Fitting on the Riemann Sphere.
International Conference on Computing in High
Energy and Nuclear Physics
, Padova, Italy; February,
2000.
Thomas S., Chan, Y., Cramer-Rao Lower Bounds for
Estimation of a Circular Arc Center and Its’ Radius.
CVGIP: Graphics Model and Image Processing, Vol.
57, No. 6, pages 527-532, 1995.
Witte, L.. Least Squares Fitting of a Great Circle Through
Points on a Sphere.
Communications of the ACM,
Volume 3, No. 11, November 1960, pp. 611-613.
Zelniker E., Clarkson, I., A Statistical Analysis Least-
Squares Circle-Centre Estimation. In
IEEE
International Symposium on Signal Processing and
Information Technology
, December 2003, Darmstadt,
Germany, pp 114-117.
Zelniker, E., Clarkson, I., A Generalisation of the
Delogne-Kása Method for Fitting Hyperspheres.
Thirty-Eighth Asiomar Conference on Signals,
Systems and Computers.
Pacific Grove, California,
November 2004.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
256
