CONTINUOUS EDGE GRADIENT-BASED
TEMPLATE MATCHING FOR ARTICULATED OBJECTS
Daniel Mohr and Gabriel Zachmann
Clausthal University, Germany
Keywords:
Template matching, Deformable object detection, Confidence map, Edge feature, Graphics hardware.
Abstract:
In this paper, we propose a novel edge gradient based template matching method for object detection. In
contrast to other methods, ours does not perform any binarization or discretization during the online matching.
This is facilitated by a new continuous edge gradient similarity measure. Its main components are a novel edge
gradient operator, which is applied to query and template images, and the formulation as a convolution, which
can be computed very efficiently in Fourier space. We compared our method to a state-of-the-art chamfer based
matching method. The results demonstrate that our method is much more robust against weak edge response
and yields much better confidence maps with fewer maxima that are also more significant. In addition, our
method lends itself well to efficient implementation on GPUs: at a query image resolution of 320 × 256 and a
template resolution of 80 × 80 we can generate about 330 confidence maps per second.
1 INTRODUCTION
Detection and tracking of articulated objects is used
in many computer vision applications.
Our long-term goal is precise tracking of the hu-
man hand in order to be able to use it as a dextrous
input device for virtual environments and many other
applications.
An important initial step in object tracking is to
localize the object in the 2D image delivered by the
camera. This is a challenging task especially with
articulated objects, due to the huge state space and,
possibly, time constraints. Most approaches formu-
late tracking of articulated objects as detecting multi-
ple objects: given a database of many objects, find the
object from the database that best matches the object
shown in the input image. This also involves find-
ing the location in the input image where that best
match occurs.Typically, the database consists of im-
ages, called templates. This can result in a database
size of thousands of templates.
A powerful method to match templates is to compare
the edge images of template and input image.
In this paper, we propose a novel method for tem-
plate matching based on edge features, which is ro-
bust against varying edge response. To this end, we
propose a novel similarity measure between a tem-
plate and the query image that utilizes the continuous
edge gradient (orientation and intensity). The input to
our algorithm is a query image and a set of templates.
The output is a confidence map. It stores for each po-
sition in the query image the index and similarity of
the best matching template.
In subsequent steps, this confidence map can be
used directly to extract the best match, or it can be
combined with other confidence maps using different
features. This is, however, not our focus here.
Our method does not perform any binarization
or discretization during the online matching process.
By contrast, all current methods based on edge dis-
tance/similarity need binary edge images. This incurs
thresholds that are difficult to adjust automatically,
which reduces the robustness of these approaches.
We utilize the orientation and intensity of edges
of both the templates and the query images directly
in our similarity measure. By contrast, most current
methods discretize edge orientations into a few inter-
vals, which renders the similarity measure discontin-
uous with respect to rotation of the object.
Our method is well suited for a complete imple-
mentation in the stream processing model (e.g., on
modern GPUs), which allows for extremely fast tem-
plate matching.
519
Mohr D. and Zachmann G. (2009).
CONTINUOUS EDGE GRADIENT-BASED TEMPLATE MATCHING FOR ARTICULATED OBJECTS.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 519-524
DOI: 10.5220/0001800805190524
Copyright
c
 SciTePress

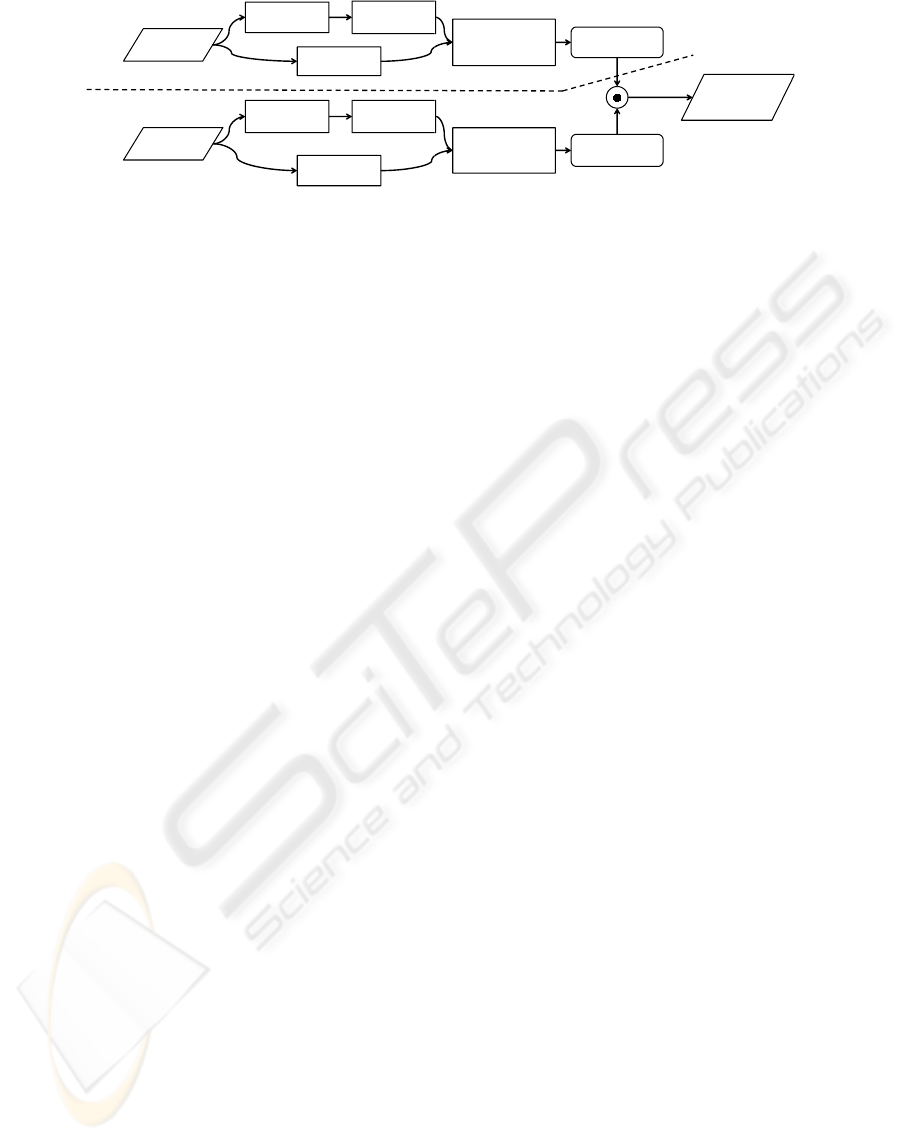
Set of
Templates
Binary Edge
Extraction
Edge Orienta-
tion
Extraction
Orientation
Mapping (3.2)
Preprocessing
tion
Extraction
Edge Intensity
Extraction
Orientation
Mapping (3.2)
Preprocessing
Online
Computation
Query
Image
Extraction
Edge Orienta-
tion Extraction
Mapping (3.2)
Online
Computation
Preprocessing for
later Similarity
Computation (3.3)
Template Set in
Fourier Space
Computation (3.3)
Set of
Confidence
Maps
Edge Importance
Transform. (3.4)
Query Image in
Fourier Space
Figure 1: Overview of our approach. The numbers in parentheses denote the section describing the respective stage.
2 RELATED WORK
The most often used edge based approaches to tem-
plate matching in the field of articulated object detec-
tion use the chamfer (Barrow et al., 1977) and Haus-
dorff (Huttenlocher et al., 1993) distance. Chamfer
matching for tracking of articulated objects is, for
example, used by (Athitsos and Sclaroff, 2001) and
(Gavrila and Philomin, 1999), the Hausdorff distance
by (Olson and Huttenlocher, 1997). The generalized
Hausdorff distance is more robust to outliers. The
chamfer distance can be implemented as convolution,
when used to generate a confidence map. Thus, it can
be computed much faster. Both, chamfer and Haus-
dorff distance can be modified to take edge orienta-
tion into account with limited accuracy. One way to
do this is to split the template and query images into
b separate images. Each contains only edge pixels
within a predefined orientation interval.
(Thayananthan et al., 2006), (Stenger et al., 2006).
To achieve some robustness against outliers, (Stenger
et al., 2006) additionally limited the nearest neighbor
distance by a predefined upper bound. A disadvan-
tage of these approaches is, the discretization of the
edge orientations, which can cause wrong edge dis-
tance estimations.
(Olson and Huttenlocher, 1997) integrated edge
orientation into the Hausdorff distance. They mod-
eled each pixel as a 3D-vector, containing pixel coor-
dinates and edge orientation.
The maximum norm is used to calculate the pixel-
to-pixel distance. (Sudderth et al., 2004) presented a
similar approach to incorporate edge position and ori-
entation into chamfer distances.
Because it cannot be formulated as convolution,
it results in high computation times. Edge orienta-
tion information is also used by (Shaknarovich et al.,
2003) as a distance measure between templates. They
discretized the orientation into four intervals and gen-
erate an orientation histogram. They do not take the
edge intensity into account. Consequently the weight
of edge orientations resulting from noise is equal to
that of object edges. This results in a very noise sen-
sitive algorithm.
3 THE CONTINUOUS EDGE
IMAGE SIMILARITY
MEASURE
Before describing our approach, we introduce the fol-
lowing notation:
T = {T
k
|k = 0 ···l − 1} is a set of templates,
W
k
× H
k
is the size of T
k
,
E
T
k
is the binarized edge image of T
k
,
I
Q
a query image of size W
Q
× H
Q
,
I
O,k
Q
⊂ I
Q
a sub-image of size W
k
× H
k
and centered
at O ∈ [0,W
Q
] × [0, H
Q
],
E
Q
the edge intensity image of I
Q
, and
S
I
Q
(k, O) a similarity measure between I
O,k
Q
and T
k
with the co-domain [0,1], in the sense that the value 1
indicates a perfect match.
The goal of a template matching algorithm is to
find the template index
¯
k that is most similar to the
target object in the image and its correct image coor-
dinates
¯
O. This can be achieved in two steps: First,
calculate the image similarities for some or all O and
k. Second, based on the similarities, obtained in step
1, choose an appropriate
¯
k and
¯
O to represent the ob-
ject state and position. The latter is not the focus of
this paper. Due to loss of information salient features
are needed to get results of high quality. Edges are
such a feature. They are fairly robust against illumi-
nation changes and varying object color.
However, edges are not completely independent
from illumination, color, texture, and camera param-
eters.Therefore, a robust algorithm for efficient tem-
plate matching is needed.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
520

3.1 Overview of Our Approach
Our approach consists of two stages. First, the tem-
plate set T and the query image I
Q
are preprocessed
to allow efficient edge-based template matching; sec-
ond, the matching itself is performed, which com-
putes a similarity value for all templates T
k
and all
sub-images I
O,k
Q
for all query image pixels O.
The templates are preprocessed in two steps. First,
we generate images of the object in different states
and viewpoints. An edge extractor is used to obtain a
binary edge image. Then, we extract the edge gradi-
ent at the edge pixels. This gradient is then mapped
in a way so that they can be compared easily and cor-
rectly. Second, we transform the template image such
that the similarity between template and query image
can be calculated efficiently by a convolution (Sec-
tion 3.2).
Before computing similarities, we extract the edge in-
tensities and gradients from the query image and map
them, just like the preprocessing for the templates.
In order to overcome the problem of multiple edges,
caused by noise, shadows, and other effects, we fur-
ther transform the image appropriately.
3.2 Computing the Similarity of Edge
Images
In this section, we describe the core of our approach,
the matching of a template T
k
and a query image I
Q
.
We assume we are given the following information:
L
T
k
= {O | E
T
k
(O) = 1}, the edge pixel list;
ˆ
G
T
and
ˆ
G
Q
, the mapped edge gradients of the tem-
plate and query image, resp., additionally each vector
normalized to length one;
N (x) = {x + y |y ∈ [−n, n]
2
},n ∈ N, a neighborhood
of x;
K, a unimodal function (kernel function) with the
maximum at K(0) = 1, and
K
n
, a kernel function with bounded support:
K
n
(∆,h) =
(
K(
∆
h
) k∆k
∞
≤ n
0 otherwise
(1)
First we map the image edge gradients such that they
can be compared by a simple multiplication without
any loss of accuracy. The mapping function
ˆ
v = f (v)
is defined as follows:
θ = arctan
v
y
v
x
(2)
θ
0
=
(
θ θ ≥ 0
θ + π θ < 0
(3)
ˆ
v = ( ˆv
x
, ˆv
y
) = kvk
2
· (cos(2θ
0
),sin(2θ
0
)) (4)
Figure 2: In order to achieve a consistent gradient distance,
we map gradients as shown here, before actually comparing
them. That way, our edge similarity measure returns low
“distances” for the edge gradients in both situations shown
here. The v
i
denote the original gradients, u
i
are intermedi-
ate ones, and w
i
are the final ones that are further used.
Figure 2 illustrates the problem and our mapping. As
explained previously, we do not have a discrete set
of edge pixels in the query image, and, thus, can-
not calculate directly a distance from each edge pixel
e ∈ L
T
k
to the closest edge pixel in I
Q
. Instead, we
use probabilities to estimate the distance: the higher
the probability and the nearer a pixel in the query im-
age is to a template edge pixel, the lower the distance
should be.The mean probability of a neighborhood of
e is used as inverse distance measure, so that a small
distance results in a high mean value and vice versa.
The weight of the neighboring pixels is controlled by
the choice of the kernel function K and its parameter
h. Because only close pixels are relevant for the simi-
larity measure, we only take into account a neighbor-
hood of each template edge pixel of size n ∈ N.
To compute the similarity S
I
Q
(k, O), we calculate
for each edge pixel e in the template image the proba-
bility P
O,k
(e) that an edge in the query image is close
to it:
P
O,k
(e) =
1
2
+
1
C
K
∑
p∈N (e)
h
K
n
(p − e, h) ·
E
Q
(O + p)
ˆ
G
T
(e) ·
ˆ
G
Q
(O + p)
i
(5)
with the normalization factor
C
K
= 2 ·
∑
p∈N (e)
K
n
(p − e, h) (6)
Note that
ˆ
G
T
(e) ·
ˆ
G
Q
(O + p) is a 2D scalar product;
because this is in [−1,1], we have to use an offset.
Figure 3 illustrates the idea behind this measure.
Then, we define the overall similarity as the mean
probability
S
I
Q
(k, O) =
1
|L
T
k
|
∑
e∈L
T
k
P
O,k
(e) (7)
CONTINUOUS EDGE GRADIENT-BASED TEMPLATE MATCHING FOR ARTICULATED OBJECTS
521

Figure 3: We estimate the similarity between a template
edge (dashed line) and a query image edge, which is rep-
resented by intensities (gray solid curves), by multiplying a
kernel that is centered around each template edge pixel (cir-
cles) with the edge intensities. The intensity value of the
template edge pixel (triangles) visualize the “closeness” of
query image edges.
Since the kernel function K and parameters h and n
are fixed, the normalization factor C
K
is constant.
We insert Eq. 5 into Eq. 7 and rewrite to
S
I
Q
(k, O) =
1
2
+
1
|L
T
k
|
∑
e∈L
T
k
∑
p∈N (e)
η
T
(p,e)η
Q
(O+p)
(8)
with
η
T
(p,e) = C
−1
K
K
n
(p − e, h)
ˆ
G
T
(e) (9)
η
Q
(x) = E
Q
(x)
ˆ
G
Q
(x) (10)
Because K
n
is zero everywhere outside its support, we
can rewrite the inner sum as a sum over all pixels in
T
k
. Similarly, the outer sum can be rewritten, yielding
We rewrite again:
1
2
+
∑
x∈D
k

η
Q
(O,x)
1
|L
T
k
|
∑
y∈D
k
E
T
k
(y)η
T
(x,y)
| {z }
˜
E
T
k
(x)

(11)
where D
k
= [0,W
k
] × [0,H
k
]. Notice that
˜
E
T
k
can be
calculated offline. Finally, we arrive at
S
I
Q
(k, O) =
1
2
+
∑
x∈D
k
η
Q
(O + x) ·
˜
E
T
k
(x). (12)
S
I
Q
(k) is called the confidence map of I
Q
and T
k
and is basically generated by correlating
˜
E
T
k
with
E
Q
ˆ
G
Q
.
The image
˜
E
T
k
is flipped. Then it can be calcu-
lated efficiently in Fourier space by a convolution.
Since η
T
,η
Q
∈ R
2
, we compute Eq. 12 independently
for each component, x and y, so that they are scalar-
valued correlations.
So far, we have described a robust and fast method
to compute the edge similarity between a query im-
age and a set of templates. One remaining problem
is that a query image often contains multiple edges
close to each other, which are, therefore, also close to
p
v
image space
value
Figure 4: 1D example of our quality measure: the true loca-
tion p of the target object is determined manually, v
p
is the
value in the combined confidence map. Our quality mea-
sure is basically the sum of the signed gray areas over the
whole confidence map.
the appropriate template edge. For instance, a cable,
which produces a shadow, causes four instead of two
strong edges. Depending on the edge orientation, this
causes severe over- or underestimation of P
O,k
(e). To
overcome this problem, we preprocess the query im-
age. We use the maximum of edge intensity weighed
kernels as new intensity. The orientations are calcu-
lated as the intensity weighted average of the neigh-
borhood. Due to space limitations we have to refer to
our technical report (Mohr and Zachmann, 2009) for
a detailed description.
The final template matching process is imple-
mented very efficiently as convolution using the
CUDA programming environment (Nvidia, 2008).
For more details please take a look at (Mohr and
Zachmann, 2009).
4 RESULTS
In our datasets, we use the human hand as the ob-
ject to be detected. In this research field, the chamfer
based matching is the most often used. Therefore, we
compare our method with the chamfer matching algo-
rithm.
For comparison, we need an appropriate measure
for the ability of the methods to localize an object at
the correct position in the query image. Given a query
image I
Q
, both the chamfer and our method generate
a confidence map S
I
Q
(k) for each template T
k
. Now
let (ˆx, ˆy) be the true location of the object in the query
image. The matching value at ( ˆx, ˆy) of the template,
delivering the best match according to the approach
used, is denoted with ˆc. Obviously, the fewer values
in all confidence maps are better than ˆc, the better the
matching algorithm is.
1
This is the idea of our quality measure of the match-
ing algorithms. We first define the combined confi-
dence map S
I
Q
of l templates: it stores for each pixel
1
The chamfer matching returns distances, not similari-
ties, but the chamfer matching output can be converted eas-
ily into similarities by inverting them.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
522

1.a 1.b 1.c 3.a 3.b
2.a 2.b 2.c 3.c 4
Figure 5: One frame of each of our three datasets: pointing hand (1.), open hand (2.), open-close gesture (3.). The orig-
inal images are denoted with the letter a, the combined confidence map generated by chamfer matching with b, and those
generated by our approach with c. Notice that with our approach, the maxima in our confidence maps are much more
significant. Full videos comparing our approach to chamfer matching based confidence maps can be found at http://cg.in.tu-
clausthal.de/research/handtracking/index.shtml. Image 4 shows a rendered template used for matching.
the confidence map value of the template that matches
best at this location, i.e.
S
I
Q
(x,y) = max
k∈[0,l−1]

S
I
Q
(k, x, y)

(13)
In detail, we use the following quality measure:
Q
I
Q
=
1
N
∑
0≤x<W
Q
0≤y<W
H

S
I
Q
( ˆx, ˆy) − S
I
Q
(x,y)

(14)
with the normalization factor N =W
Q
H
Q
(max−min).
Min and max are the smallest and largest value in S
I
Q
,
resp. We manually determined the true object posi-
tions ( ˆx, ˆy). Thus, the higher the value Q
I
Q
, the better
the method works for the query image and template
set. Figure 4 illustrates the measure by means of a
1D combined confidence map. The correct template
index is not taken into account in the quality measure.
But, we observed that at the true position, the best
matching template reported by our algorithm looks
very similar to the object in the input image in most
frames (see URL at Figure 5).
As test data we used RGB images of resolution
320 × 256.
All image preprocessing is done on the graphics
hardware in CUDA. We used three datasets for evalu-
ation (Figure 5). Dataset 1, consisting of 200 frames,
is a pointing hand moving in the image. The templates
are 300 renderings of an artificial 3D hand model rep-
resenting a pointing gesture. Each template is gener-
ated from a different camera viewpoint. In dataset 2,
an open hand is tested. The length of the dataset is
200 frames, too, and the number of templates is 300
as well. Dataset 3 shows an open-closing sequence of
a human hand, consisting of 135 frames. Again, the
templates are created using the 3D hand model, with
its fingers opening and closing, rendered from three
different camera angles. The average template size is
about 80 × 80. As kernel function we have chosen
the Gaussian function K(x) = e
−
1
2
x
2
. The bandwidth
parameter h, needed in Eq 1, has been manually op-
timized; it depends only on the templates, not on the
query images. We set n = d3he (three sigma rule for
Gaussians) and h = 3.3 for dataset 1 and h = 4.0 for
datasets 2 and 3. For the chamfer matching algo-
rithm we used the parameters proposed by (Stenger
et al., 2006) (6 edge orientation channels and a dis-
tance threshold of 20).
Figure 5 shows an example frame and its com-
bined confidence map for each dataset. Figure 6
shows the quotient Q
GM
/Q
CF
of the quality measure
of the two approaches for all frames. Q
GM
denotes
the quality measure for our approach and Q
CF
for the
chamfer based approach. Clearly, in most parts of
datasets 1 and 3 our approach works better than cham-
fer based method. Only in the last third of dataset 2,
chamfer matching works better. In these frames, none
of the templates matches well the orientation of all
fingers. Closer inspection suggests that a lot of orien-
tations in these frames happen to be discretized to the
right bin in the chamfer based method. This makes it
produce a better match with the right template.
We measured a frame-rate of about 1.1 fps with
our datasets. This comprises the preprocessing of the
query images and the convolution with 300 templates.
The limiting factor of the computation time of the
matching process is the FFT. It consumes over 90%
of the total time.
CONTINUOUS EDGE GRADIENT-BASED TEMPLATE MATCHING FOR ARTICULATED OBJECTS
523

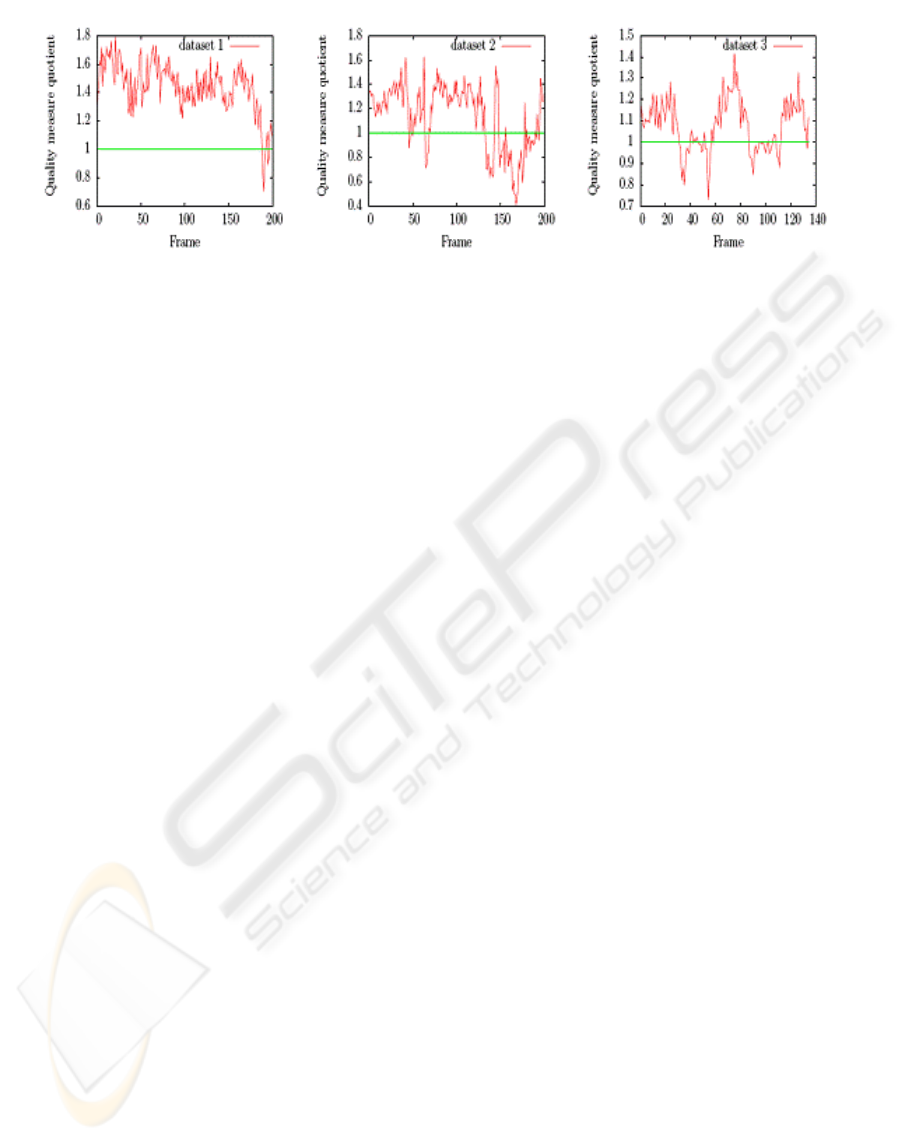
Figure 6: Each plotshows the quotient of the quality between our approach and the chamfer based approach. A value greater
than 1 indicates that our approach is better.
5 CONCLUSIONS
In this paper, we developed an edge similarity mea-
sure for template matching that does not use any
thresholds nor discretize edge orientations. Conse-
quently, it works more robustly under various condi-
tions. This is achieved by a continuous edge image
similarity measure, which includes a continuous edge
orientation distance measure. Our method is imple-
mented as convolution on the GPU and thus is very
fast. We generate a confidence map in only 3 ms. The
confidence maps can easily combined with other fea-
tures to further increase the quality of object detec-
tion.
In about 90% of all images of our test datasets, our
method generates confidence maps with fewer max-
ima that are also more significant. This is better than
a state-of-the-art chamfer based method, which uses
orientation information as well.
In the future, we plan to test anisotropic and asym-
metric kernels for the preprocessing of the templates
in order to exploit the knowledge of inner and outer
object regions. This should improve matching qual-
ity. Furthermore, we will research methods to auto-
matically select the kernel bandwidth parameter.
REFERENCES
Athitsos, V. and Sclaroff, S. (2001). 3d hand pose estima-
tion by finding appearance-based matches in a large
database of training views. In IEEE Workshop on Cues
in Communication.
Barrow, H. G., Tenenbaum, J. M., Bolles, R. C., and Wolf,
H. C. (1977). Parametric correspondence and chamfer
matching: Two new techniques for image matching.
In International Joint Conference on Artificial Intelli-
gence.
Gavrila, D. M. and Philomin, V. (1999). Real-time object
detection for smart vehicles. In IEEE International
Conference on Computer Vision.
Huttenlocher, D., Klanderman, G. A., and Rucklidge, W. J.
(1993). Comparing images using the hausdorff dis-
tance. In IEEE Transactions on Pattern Analysis and
Machine Intelligence.
Mohr, D. and Zachmann, G. (2009). Continuous edge
gradient-based template matching for articulated ob-
jects. In Technical Report.
Nvidia (2008). Compute unified device architecture.
Olson, C. F. and Huttenlocher, D. P. (1997). Automatic tar-
get recognition by matching oriented edge pixels. In
IEEE Transactions on Image Processing.
Shaknarovich, G., Viola, P., and Darrell, T. (2003). Fast
pose estimation with parameter-sensitive hashing. In
IEEE International Conference on Computer Vision.
Stenger, B., Thayananthan, A., Torr, P. H. S., and Cipolla,
R. (2006). Model-based hand tracking using a hierar-
chical bayesian filter. In IEEE Transactions on Pattern
Analysis and Machine Intelligence.
Sudderth, E. B., Mandel, M. I., Freeman, W. T., and Will-
sky, A. S. (2004). Visual hand tracking using nonpara-
metric belief propagation. In IEEE CVPR Workshop
on Generative Model Based Vision.
Thayananthan, A., Navaratnam, R., Stenger, B., Torr, P.,
and Cipolla, R. (2006). Multivariate relevance vector
machines for tracking. In European Conference on
Computer Vision.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
524