
EQ
UATION DISCOVERY FOR MACROECONOMIC MODELLING
Dimitar Kazakov
Department of Computer Science, The University of York, YO10 5DD, York, U.K.
Tsvetomira Tsenova
European Central Bank, Frankfurt am Mein, Germany
Bulgarian National Bank, Sofia, Bulgaria
Keywords:
Machine learning, Equation discovery, LAGRAMGE, Macroeconomic modelling, Inflation.
Abstract:
This article describes a machine learning based approach applied to acquiring empirical forecasting models.
The approach makes use of the LAGRAMGE equation discovery tool to define a potentially very wide range of
equations to be considered for the model. Importantly, the equations can vary in the number of terms and types
of functors linking the variables. The parameters of each competing equation are automatically fitted to allow
the tool to compare the models. The analysts using the tool can exercise their judgement twice, once when
defining the equation syntax, restricting in such a way the search to a space known to contain several types
of models that are based on theoretical arguments. In addition, one can use the same theoretical arguments to
choose among the list of best fitting models, as these can be structurally very different while providing similar
fits on the data. Here we describe experiments with macroeconomic data from the Euro area for the period
1971–2007 in which the parameters of hundreds of thousands of structurally different equations are fitted and
the equations compared to produce the best models for the individual cases considered. The results show the
approach is able to produce complex non-linear models with several equations showing high fidelity.
1 INTRODUCTION
Understanding the nature of the inflation process is a
central issue in macroeconomics.
1
The private agents,
businesses and households alike, are interested in its
forecasting, as expectations on inflation, and other
key macro-variables, affect the way in which they
make their investment and saving decisions and nego-
tiate labour contracts. Policy makers, especially those
in charge of monetary policy, are interested in both
forecasting and control of inflation.
The general characteristics of the inflation pro-
cess, as well as the structure of the economy are
evolving through time. After the 1980s, inflation lev-
els have declined in the industrialised countries, coin-
ciding with low volatility of both inflation and output,
less pronounced and shorter business cycles (Stock
and Watson, 2003). Many have speculated on the
potential sources of this phenomenon, also known as
1
All
opinions are those of the authors and do not imply
agreement or endorsement by the European Central Bank or
the University of York.
the Great Moderation — successful monetary policy,
globalisation, financial markets developments (over-
coming of financial costs and borrowing constraints
for both residential and business investment), or good
fortune. With the sudden collapse of the financial
markets in the last few weeks, it is possible that this
period of stability may be followed by a transitional
period while the system switches to a new regime.
This is likely to further fuel the discussion on the un-
derstanding of the underlying processes and the way
in which they are modelled. We believe that this dis-
cussion should be informed by both theoretical insight
and analysis of the empirical data.
With this work, we want to attract the attention
to a machine learning approach, combining these two
aspects through the search for empirical models in
which the chosen functional dependencies between
the system variables are economically sound, but the
actual functional form of these dependencies is se-
lected from a much wider than usual spectrum of
options. We use a dataset of macroeconomic ob-
servations from the Euro area and supply the LA-
318
Kazakov D. and Tsenova T. (2009).
EQUATION DISCOVERY FOR MACROECONOMIC MODELLING.
In Proceedings of the International Conference on Agents and Artificial Intelligence, pages 318-323
DOI: 10.5220/0001802403180323
Copyright
c
SciTePress

GRAMGE equation discovery tool used here with a
range of grammars describing the possible syntax
(functional terms, dependencies between variables,
maximum complexity) of each equation. The recur-
sive empirical models produced as a result are tested
on their ability to (1) predict the next state of the sys-
tem from past observations for the data used to learn
the model (i.e., using training data to measure the “in-
sample” error), (2) predict the next state from past ob-
servations for data not used in the training (using the
test data to measure “out-of-sample” error), and, fi-
nally, (3) forecast the future of the system (parameter
in question) starting from the last observation used in
training, and recursively using the model’s own pre-
dictions to look another step ahead in time. The re-
sults suggest that the empirical approach is able to re-
produce the results of other approaches, when simi-
larly constrained, and go further to produce complex
nonlinear models able to forecast inflation over con-
siderable periods of time.
2 BACKGROUND
2.1 Empirical Modelling of the Inflation
Process
In addition to the observed decline in inflation volatil-
ity in recent years, the inflation had grown increas-
ingly disconnected from other macro variables. The
inflation process can be modelled as a function of its
own history, in which the possibility of a time trend
is also taken into account. Linear estimations of that
kind are known to produce forecasts that are hard to
outperform in terms of out of sample accuracy. There-
fore, the first model to consider here is a univariate
autoregressive model of the general form:
π
t
= f (π
t−1
, π
t−2
. . . π
t−k
, t) (1)
where π
t
is the inflation rate and t is time.
This type of modelling does not provide, however,
a satisfactory understanding on the co-movement and
dependence between the nominal and the real side of
the economy (i.e., inflation and output) and how these
are influenced by monetary policy (interest rates).
Economic theory suggests that inflation is linked to
output y (Eq. 3), more specifically, it rises when
output increases over a certain level, a relationship
known as the Phillips curve. Similarly, output is cor-
related with the interest rate r (Eq. 2), and is expected
to rise when interest rates are lowered, a relationship
known as the IS (Investment and Saving) curve (Blan-
chard, 2000). Monetary policy is supposed to react to
inflation, as well as the state of the economy mea-
sured through its output, which is a relationship re-
flected in Eq. 4. Here the most common approach is
to model these three equations as linear functions. It is
suggested though that due to the constantly evolving
structure of the economy, a linear specification could
fail in capturing those relationships and might under-
estimate their value for forecasting.
y
t
= f (y
t−1
, y
t−2
, ...r
t
, r
t−1
, ...t) (2)
π
t
= f (π
t−1
, π
t−2
, ...y
t
, y
t−1
, ...t) (3)
r
t
= f (π
t
, π
t−1
, ...y
t
, y
t−1
, ..., t) (4)
2.2 Machine Learning, Equation
Discovery and LAGRAMGE
Machine Learning (ML) aims at describing the prop-
erties of a set of observations from a given source,
and/or making predictions about the nature of future
observations from the same source. Both goals are
achieved by changing the representation of available
data as expressed in its original form (or object lan-
guage) into another representation (using another for-
malism, known as hypothesis language). The new
representation copies closely the information encoded
in the original data, but is usually more general, and
allows statements to be made about yet unseen cases.
ML can be seen as the search for a mapping from a set
of inputs to an output; this mapping is often a func-
tion. In the context of searching for macroeconomic
models, this means functional relationships between
the observed variables can be determined.
No ML algorithm can make predictions unless it
employs a bias (Mitchell, 1997). In general, the bias
will restrict the range of possible functions (models,
hypotheses) that can be described by the hypothe-
sis language. For instance, the set of data points
{(0, 0), (π, 0), (2π, 0)} can be modelled by the func-
tions y = 0, y = cos x or y = x(x − π)(x − 2π), de-
pending on the bias, which may restrict the hypothesis
to a linear, trigonometric or polynomial function.
Such a bias is also called language bias to distin-
guish it from the preference bias, allowing a choice
between alternative models with equal coverage of
the available data. Here some simple, but general
principles (heuristics) are often employed. For in-
stance, Occam’s razor (Mitchell, 1997) favours the
simplest hypothesis language, while the Minimal De-
scription Length (MDL) bias (Rissanen, 1978) sug-
gests a trade-off between the complexity of the hy-
pothesis language and that of the resulting represen-
tation of the data.
The area of ML focusing on the search for quanti-
tative laws, expressed as equations, is known as equa-
EQUATION DISCOVERY FOR MACROECONOMIC MODELLING
319

Table 1: Sample data.
Quarter/Year π y r
1971Q1 5.25 4.22 0.68
1971Q2 5.83 3.56 -0.16
1971Q3 6.09 3.92 -0.14
1971Q4 6.36 3.50 -0.21
.
.
.
.
.
.
.
.
.
.
.
.
2007Q1 1.87 3.07 1.93
tion discovery. The system LAGRAMGE (Todorovski
and D
ˇ
zeroski, 1997) is one example of this approach.
When an initial draft of the equation is provided, the
process is known as equation revision (Todorovski
and D
ˇ
zeroski, 2001). In this case, initial input is re-
quired from experts, but the changes carried out by the
learner can be non-trivial, and result in large improve-
ments (Todorovski et al., 2003). A unique feature of
LAGRAMGE is its use of a user-defined context-free
grammar to define a potentially different language
bias for each modelling task. Here the range of pos-
sible equations is defined at a symbolic level, and the
actual parameters (constants) of the equations consid-
ered in the search are fitted automatically in the pro-
cess. A set of simple constraints, such as the maxi-
mum depth of the equation parse tree, are employed
to prune the search and make it feasible. Even with
such restrictions, the search is often conducted over a
potential range of hundreds of thousands of different
equations. LAGRAMGE can also be set to use a form
of an MDL preference bias to penalise for additional
complexity of the equations found.
2.3 The Euroarea Dataset
The dataset used consists of quarterly data of the an-
nual rates of inflation π, output growth y, and the
nominal interest r for the Euro area in the period
1971Q1–2007Q1 (see Table 1). The dataset was di-
vided into data used for model estimation (i.e., train-
ing sample/dataset, comprising all readings in the pe-
riod 1971Q1–2005Q1), and a test dataset 2005Q2–
2007Q1, which was used to evaluate the models on
previously unseen data (“out-of-sample evaluation”).
Wherever the real interest rates were needed, they
were assumed to be equal to the nominal interest rates
minus the realised (i.e., actual) inflation one period
ahead, the latter being used as a proxy for the ex-
pected inflation rate.
2.4 Experimental Design
All models are obtained by designating an output
variable in the dataset, and specifying the range of
other variables that are to be considered as indepen-
dent variables in the equation. This is repeated un-
til equations for all output variables in the model are
obtained. We also have to specify the operators and
functors that may appear in each equation. In all
cases, the equations can be expressed as sums of some
the following types of terms:
• A constant: c.
• A product of a constant and a variable: c
i
.V
i
.
• A product of a constant and two variables:
c
i
.V
i
.V
j
.
• A product of a constant, a variable, and a sin func-
tion of a linear function of the same or other vari-
able: c
i
.V
i
.sin(c
j
.V
j
+ c
k
).
• A product of a constant, and two sin func-
tions with arguments as above: c
i
.sin(c
j
.V
j
+
c
k
).sin(c
l
.V
l
+ c
m
).
The above range makes possible to describe a
range of linear and non-linear equations that will be
considered by the learner.
3 RESULTS AND EVALUATION
Firstly, we estimate a baseline linear autoregressive
model – inflation as a function of its previous two
values – using standard tools (Matlab). The resulting
equation is:
π
t
= 0.04 + 1.49π
t−1
− 0.50π
t−2
+ ε
t
ε ∼ iid N
¡
0, σ
2
¢
(5)
where ε is the model’s error. Using LAGRAMGE
to perform the same task produces the following equa-
tion:
π
t
= 0.06 + 1.38π
t−1
− 0.40π
t−2
+ ε
t
(6)
The evaluation of the accuracy of the models is
performed according to the root mean squared error
(RMSE), and mean absolute error (MAD).
The baseline and the LAGRAMGE model have al-
most identical accuracy - with the out of sample ac-
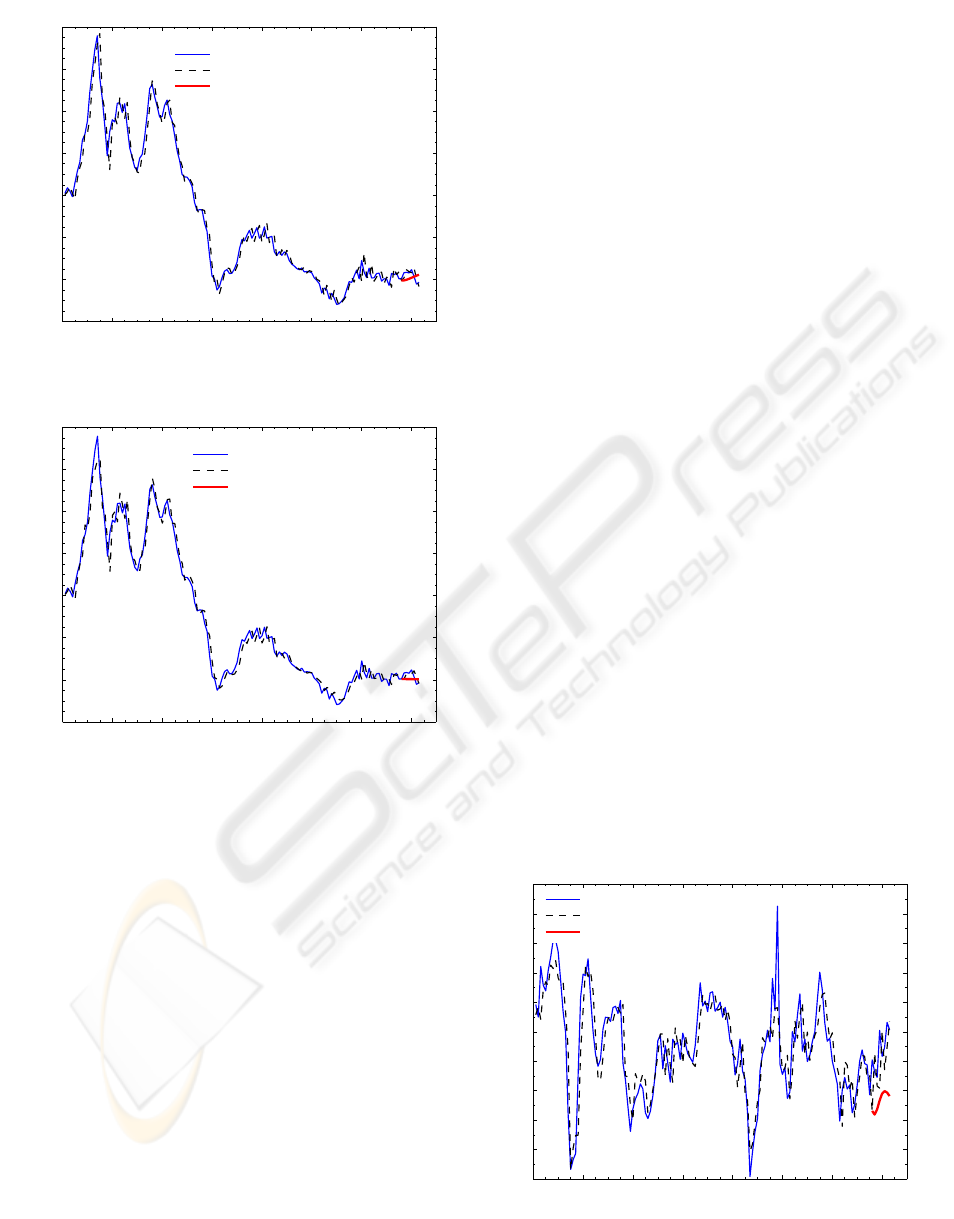
curacy greater than the in-sample accuracy. Figure
1 shows the in-sample fit (up to 2005Q1) and out of
sample (from 2005Q2 onwards) forecasts.
Non-linear models relax the language bias and al-
low for potentially more complex and accurate mod-
els (Clements et al., 2004). The full capabilities of
LAGRAMGE are used when looking for non-linear
specifications. The best equation has an infinitesimal
time trend which is unlikely to be significant. (It also
produces inferior out of sample forecasts). Therefore
we skip to the second-best equation, reported below:
ICAART 2009 - International Conference on Agents and Artificial Intelligence
320
75Q4 80Q4 85Q4 90Q4 95Q4 00Q4 05Q4
2
4
6
8
10
12
14
Actual
One step ahead estimation and forecast
Recursive forecast
Figure 1: Inflation π: actual rate (in %) vs linear model one-
step-ahead forecast and recursive out-of-sample forecast.
75Q4 80Q4 85Q4 90Q4 95Q4 00Q4 05Q4
0
2
4
6
8
10
12
14
Actual
One step ahead estimation/forecast
Recursive − out of sample
Figure 2: Inflation π: actual rate (in %) vs non-linear model
one-step-ahead forecast and recursive out-of-sample fore-
cast.
π
t
= −0.51 + 0.89π
t−1
+
3.26sin(−0.19π
t−2
+ 1.99) −
2.51sin(−0.28π
t−1
− 4.12) (7)
The accuracy of this non-linear autoregressive
model is shown in Fig. 2.
The next class of models learned assumes that
forecasts are based on a system of equations, as de-
scribed in Eq. 2–4. The best equation, in terms of
in-sample fit, on the real interest rate provides us with
the following equation:
r
t
= (8)
6.98 + 0.05y
t−2
+
8.88sin(0.09r
t−1
− 32.21) sin(0.05π
t−1
+ 14.18) +
23.14sin(0.01π
t−2
+ 0.01) sin(0.045t −1.78) + ε
t
For the output we choose the third best equation,
since the previous two have an insignificant trend and
are rejected on theoretical grounds:
y
t
= (9)
1.60 + 0.07y
t−2
+
8.84sin(0.11r
t−2
+ 1.20) sin(0.58y
t−1
+ 0.84) +
10.66sin(0.56y
t−1
− 2.02) sin(0.11y
t−2
+ 0.88)
The inflation equation is LAGRAMGE’s second
best and the first that satisfies the human expert:
π
t
= (10)
0.11 + 0.96π
t−1
+
6.65sin(0.60y
t−1
− 1.02) sin(0.02π
t−1
− 0.04) −
0.62sin(−0.28π
t−1
+ 0.71) sin(0.21t −1.09)
Note that the graphs in Fig.1–5 up to 2005Q1 rep-
resent the in-sample fit, that is, how well the model
anticipates a data point that has been used in extract-
ing the model. Past the 2005Q1 point, the one-step
ahead projections are true out-of-sample predictions
– LAGRAMGE had no knowledge of those data points
while learning the model; when the model is used,
each of the actual data readings was fed to the model
to predict its value in the next time interval. Out-of-
sample prediction was also carried out in a recursive
manner, starting from the last known data point, mak-
ing a one step ahead prediction, then using it as a start-
ing point to make a forecast for the next time interval.
Of course, the recursive forecast is the hardest of all,
as its errors are gradually accumulated.
The accuracy of Eq. 5–10 are evaluated in Table 2.
It is reassuring that the out-of-sample accuracy of all
equations on inflation (Eq.5–7, 10) is greater than
the in-sample accuracy, as it suggests that the mod-
els have genuinely captured some of the properties of
the system, and have predictive power, rather than just
being an overfitted model of the training data.
75Q4 80Q4 85Q4 90Q4 95Q4 00Q4 05Q4
−2
−1
0
1
2
3
4
5
6
7
8
Actual
One step ahead estimation/forecast
Recursive − out of sample
Figure 3: Output y: actual rate versus non-linear multi-
variate model one-step-ahead forecast and recursive out-of-
sample forecast.
EQUATION DISCOVERY FOR MACROECONOMIC MODELLING
321

75Q4 80Q4 85Q4 90Q4 95Q4 00Q4 05Q4
−4
−2
0
2
4
6
8
10
Actual
One step ahead estimation/forecast
Recursive − out of sample
Figure 4: Real interest r: actual rate versus non-linear mul-
tivariate model one-step-ahead forecast and recursive out-
of-sample forecast.
4 DISCUSSION
The univariate non-linear model of inflation (Eq. 7 is
the best of all; it outperforms the baseline on all mea-
sures, and its superiority is particularly evident in the
most important aspect, the recursive out-of-sample
prediction, where its error is almost half of that of the
baseline model. Some of the most recent advances in
macroeconomic modelling have
75Q4 80Q4 85Q4 90Q4 95Q4 00Q4 05Q4
0
2
4
6
8
10
12
14
Actual
One step ahead estimation/forecast
Recursive − out of sample
Figure 5: Inflation π: actual rate versus non-linear multi-
variate model one-step-ahead forecast and recursive out-of-
sample forecast.
been based on the iterative re-estimation of the
model parameters with each new observation.
Not so here – all our models hold their ground for
a period spanning 34 (resp. 36) years, without the
need for adjustment. This increases the likelihood
that they may offer some theoretical insight rather
05Q1 05Q2 05Q3 05Q4 06Q1 06Q2 06Q3 06Q4 07Q1
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
Actual
Linear univariate model
Non−linear univariate model
Non−linear multivariate model
Figure 6: Inflation π: a close-up comparison of recursive
out-of-sample forecasts.
than just being a numerical tool minimising error. The
Table 2: RMSE - root mean squared error; MAD - mean
absolute deviation.
Eqn In-sample Out-of-sample
One step ahead Recursive
RMSE MAD RMSE MAD RMSE MAD
5 0.49 0.36 0.22 0.19 0.46 0.41
6 0.49 0.36 0.22 0.19 0.46 0.41
7 0.45 0.34 0.20 0.15 0.26 0.23
8 0.56 0.45 0.64 0.52 1.15 0.87
9 0.83 0.64 1.13 0.95 1.82 1.75
10 0.38 0.30 0.23 0.16 0.31 0.26
more complex, 3-equation model performed less well,
which may be due to the fact that it combined three
different forecasts, each with its own systemic er-
ror; however, this inflation forecast still outperformed
the baseline. There are other interesting aspects of
this model—for instance, when used in a recursive
forecast mode, it can spontaneously go in and out
of an auto-oscillation regime. This is significant, as
it demonstrates the potential ability of the learner to
produce models describing different regimes (modes)
of the system within the same equations. There is a
lot more work to be done, with learning differential
equations, splitting the training data at points of ma-
jor structural changes in the EU, and modifying the
language bias being only some of the options.
REFERENCES
Blanchard, O. (2000). Macroeconomics. Prentice Hall, sec-
ond edition.
Clements, M. P., Franses, P. H., and Swanson, N. R. (2004).
Forecasting economic and financial time-series with
ICAART 2009 - International Conference on Agents and Artificial Intelligence
322

non-linear models. International Journal of Forecast-
ing, 20:169–183.
Mitchell, T. (1997). Machine Learning. McGraw-Hill.
Rissanen, J. (1978). Modeling by shortest data description.
Automatica, 14:465+.
Stock, J. and Watson, M. (2003). Has the business cycle
changed? Evidence and explanations. In FRB Kansas
City Symposium.
Todorovski, L. and D
ˇ
zeroski, S. (1997). Declarative bias
in equation discovery. In Proc. of 14
th
International
Conference on Machine Learning, pages 376–384.
Todorovski, L. and D
ˇ
zeroski, S. (2001). Theory revision
in equation discovery. In Proc. of the 4
th
Interna-
tional Conference on Discovery Science, volume 2226
of LNCS, pages 389+. Morgan Kaufmann.
Todorovski, L., D
ˇ
zeroski, S., Langley, P., and Potter, C.
(2003). Using equation discovery to revise an Earth
ecosystem model of carbon net production. Ecologi-
cal Modelling, 170:141–154.
EQUATION DISCOVERY FOR MACROECONOMIC MODELLING
323
