MULTIPLE CUE DATA FUSION USING MARKOV RANDOM
FIELDS FOR MOTION DETECTION
Marc Vivet, Brais Mart´ınez
Department of Computer Science, Universitat Aut`onoma de Barcelona, Barcelona, Spain
Xavier Binefa
Department of Information Technologies and Communications, Universitat Pompeu Fabra, Barcelona, Spain
Keywords:
Graphical model, Markov random field, Multiple cue fusion, Motion detection, Belief propagation.
Abstract:
We propose a new method for Motion Detection using stationary camera, where the information of different
motion detectors which are not robust but light in terms of computation time (what we will call weak motion
detector (WMD)) are merged with spatio-temporal Markov Random Field to improve the results. We put the
strength, instead of on the weak motion detectors, on the fusion of their information. The main contribu-
tion is to show how the MRF can be modeled for obtaining a robust result. Experimental results show the
improvement and good performance of the proposed method.
1 INTRODUCTION
The segmentation of moving objects using stationary
camera is a critical low-level vision process used as
a first step for many computer vision applications,
as for example video surveillance. This make that
obtaining good results in this first process could be
in many cases a must. One of the most common
approaches to tackle this problem consists on back-
ground subtraction.
During the last decades many backgroundsubtrac-
tion methods have been proposed. The approaches
range from naive frame differencing to more complex
probabilistic methods or from color based methods to
the use of edges. Our aim is to apport a probabilistic
framework based on Markov Random Fields (MRF)
to combine some of the simplest background subtrac-
tion algorithms to obtains robust results. The intro-
duction will therefore be divided into a brief sum-
mary of the basic existing background subtraction
techniques, a summary of MRF and its application to
our problem and finally a summary of our work.
The most naive method is the frame differenc-
ing (Desa and Salih, 2004), where movement is de-
tected whenever the difference between consecutive
frames is superior than a predefined threshold. This
method works only in particular cases and it lacks
of robustness. A better solution consists on the use
of statistical methods to model the possible aspect
of each pixel individually. Some methods obtain
the background like the average or the median of
each pixel (Lo and Velastin, 2000; R. Cucchiara and
Prati, 2003). Exponential forgetting (Koller et al.,
1994) uses a moving-window over the temporal do-
main to handel the change of lighting condition and
distinguish between moving and stationary objects.
Some other approaches uses a generative method
like Gaussian Mixture Models (Stauffer and Grim-
son, 1999), again modeling the historical aspect of
each pixel individually. In Kernel Density Estima-
tors (Ahmed M. Elgammal, 2000), the background
PDF is obtained by using the histogram of the n
most recent pixel values, each one smoothed with a
Gaussian kernel. Mean-shift based background esti-
mation (Bohyung Han, 2004) uses a gradient-ascent
method to find the modes and covariance of that PDF.
Other option is to use Hidden Markov Model (HMM)
(Rittscher et al., 2000) to impose temporal continuity
to the classification of a pixel as background or fore-
ground. One common drawback of all these meth-
ods is the lack of spatial consistency, i.e., each pixel
is modeled individually and no consistency with the
contiguous pixels is imposed.
Another family of methods, in contrast to the
529
Vivet M., Martínez B. and Binefa X. (2009).
MULTIPLE CUE DATA FUSION USING MARKOV RANDOM FIELDS FOR MOTION DETECTION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 529-534
DOI: 10.5220/0001802605290534
Copyright
c
 SciTePress

previous ones, exploits the spatial consistency, like
Eigen-background (N.M. Oliver and Pentland, 2000),
Wallflower (K. Toyama and Meyers, 1999) and MRF
based methods. In the first one, principle compo-
nent analysis (PCA) is used to model the static back-
ground. Wallflower processes images at various spa-
tial levels, pixel level, region level and frame level.
Finally the MRF based methods uses a Markov net-
work to introduce the spatial information to the pre-
vious methods. (Yin and Collins, 2007) uses MRF to
introduce spatial and temporal information to frame
differencing and (Wang et al., 2002) apply it for intro-
ducing the spatial consistency into the HMM method
previously cited (Rittscher et al., 2000).
To solve a MRF different techniques exist, like
Graph Cuts (Kohli and Torr, 2005) or Belief Propa-
gation (BP) (Yedidia et al., 2005; Weiss and Freeman,
2001). The first one finds the best approximation of
the optimum MRF state by repeatedly maximizing
the join probability using Max-flow / min-cut method
from network theory. BP interactively propagates the
probability (belief) of each node to its neighbors.
In this work, we propose a new method based
on MRF to combine different naive motion detectors,
possibly coming from different information sources,
and at the same time add spatial and temporal infor-
mation to improve the results. In that sense, this work
uses as weak motion detectors information coming
from the pixel color values, the detection of shadows
and the detection of edges. All of these methods con-
stitute a research line nowadays and none of the solu-
tions adopted in this article are optimal. Nevertheless,
each information source can be considered as an inde-
pendent module and could be replaced by a better al-
gorithm. The improvement of the results obtained by
the differentmethods on their own respect to the fused
method are remarkable and it should be remarked that
our work was to build a general framework for infor-
mation fusion rather than optimizing each source.
In the sections 2 and 3 are explained the concepts
of MRF and how it can be inferred using BP. In sec-
tion 4 are shown the our approach. Then section 5
are presented the result that we have obtained in dif-
ferent scenarios. Finally in section 6 are shown the
conclusion and the future of our work.
2 MARKOV RANDOM FIELD
Markov Random Field (Bishop, 2006; Yedidia et al.,
2005; Kindermann and Snell, 1980) is a graphical
model that can be modeled as a undirected bipar-
tite graph G = (X, F, E), where each variable node
X
n
∈ X, n ∈ {1, 2, ..., N} represents a S discrete-
valued random variable and x
n
represent the possi-
ble realizations of that random variable. Each fac-
tor node f
m
∈ F, m ∈ {1, 2, ..., M} is a function
mapping from a subset of variables {X
a
, X
b
, ...} ⊆ X,
{a, b, ...} ⊆ {1, 2, ...,N} to the factor node f
m
, where
the relation between them is represented by edges
{e
<m,a>
, e
<m,b>
, ...} ∈ E connecting each variable
node {X
a
, X
b
, ...}.
The joint probability mass function is then factor-
ized as
P(X
1
= x
1
, X
2
= x
2
, ..., X
N
= x
N
) ≡ P(x) (1)
P(x) =
1
Z
M
∏
m=1
f
m
(x
m
), (2)
where the factor f
m
has an argument x
m
that repre-
sents a subset of variables from X. Z is the partition
function defined by
Z =
∑
x
M
∏
m=1
f
m
(x
m
). (3)
We assume that the functions f
m
are non-negative
and finite so P(x) is a well defined probability distri-
bution. To infer the most probable configuration of
the graph, it is necessary to compute the marginals as,
P
n
(x
n
) =
∑
x\x
n
P(x) (4)
where x\x
n
means all the realizations in the graph ex-
cept the realizations for the node X
n
. P
n
(x
n
) means the
probability of the states of the random variable X
n
and
will denote the marginal probability function obtained
by marginalizing P(x) onto the random variable X
n
.
However the complexity of this problem grows
exponentially with the number of variables N and
thus becomes computationally intractable in the gen-
eral case. Approximation techniques such as Graph
Cuts and Belief Propagation are often more feasible in
practice. In section 3 we will explain in detail the Be-
lief Propagation algorithm, which is the method that
we have used.
3 BELIEF PROPAGATION
Belief Propagation (J.C.MacKay, 2003; Yedidia et al.,
2005; Weiss and Freeman, 2001; Felzenszwalb and
Huttenlocher, 2004) is an iterative algorithm for com-
puting marginals of functions on a graphical model.
This method is only exact in graphs that are cycle-
free. However, it is empirically proved that, even
in these cases, BP provides a good approximation of
the optimum state. There exist different approaches
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
530

depending on the problem. In some cases, BP al-
gorithms are focused in finding the maximum pos-
terior probability for all the graph like Max-Product
BP algorithm. In other cases, they are motivated
by obtaining the most probable state for each node,
like Sum-Product BP algorithm. We have selected
the Sum-Product BP algorithm because perfectly suits
our needs. A brief discussion of the practical conse-
quences of choosing any of this methods can be found
in (Felzenszwalb and Huttenlocher, 2004).
BP algorithms works by passing messages around
the graph. The sum-product version will involve mes-
sages of two types: messages q
n→m
from variable
nodes to factor nodes, defined as
q
n→m
(x
n
) =
∏
m
′
∈M(n)\m
r
m
′
→n
(x
n
) (5)
where M(n) is the set of factors in witch variable X
n
participates. And messages r
m→n
from factor nodes
to variable nodes, defined as
r
m→n
(x
n
) =
∑
x
m
\n

f
m
(x
m
)
∏
n
′
∈N(m)\n
q
n
′
→m
(x
n
′
)

(6)
where N(m) is the set of variables that the f
m
factor
depends on. Finally a belief b
n
(x
n
), that is an approx-
imation of the marginal P
n
(x
n
), is computed for each
node by multiplying all the incoming messages at that
node,
b
n
(x
n
) =
1
Z
∏
m∈M(n)
r
m→n
(x
n
) (7)
Note that b
n
(x
n
) is equal to P
n
(x
n
) if the MRF have no
cycles. In this point we have to select the more feasi-
ble state for each node. In order to do this, there exist
different criteria like Maximum a Posteriori (MAP)
and Minimum Mean Squared Error (MMSE):
• MAP (Maximum a Posteriori). For each node we
take the state x
n
with higher belief b
n
(x
n
) (Qian
and Huang, 1997).
x
MAP
n
= argmax
x
n
(b
n
(x
n
)) (8)
• MMSE (Minimum Mean Squared Error). We
make the weighted mean of each state x
n
and its
belief, given by b
n
(x
n
) and we select the x
n
that
have less squared error (Yin and Collins, 2007).
x
MMSE
n
=
∑
x
n
x
i
b
n
(x
n
) (9)
4 OUR MODEL
Our objective is to perform a good motion segmen-
tation using Weak Motion Detection (WMD) algo-
rithms, which are defined as fast and simple but not
fully reliable motion detectors. These motion algo-
rithms are selected to extract different types of infor-
mation. First of all, we will use a Background Sub-
traction Algorithm that uses a simple gaussian to rep-
resent the historical values of each pixel and then to
estimate if the pixel is part or not of a mobile object;
we will use a Motion Edge Detector, that obtains the
edges of the moving objects, doing a simple subtrac-
tion of the edges detected in a frame and the edges
detected in the background model (removing the sta-
tionary edges); the last algorithm will be a Shadow
Detector of the mobile parts. Then, in order to merge
all this information, we will model a MRF and its po-
tential function to obtain the more feasible moving
image regions for each frame in a video.
Our model is inspired in (Yin and Collins, 2007;
Wang et al., 2002). This model is represented by a
4-partite graph G = (X, D, F, H, E) where there are
two types of variables nodes and two types of fac-
tors nodes. The first type of variable nodes X
(i, j)
∈ X
represents a binary discrete-valued random variable
corresponding to the static and dynamic states that
can take each pixel in a w × h image, so we have
one X
(i, j)
for each pixel I
(i, j)
in the image and x
(i, j)
represents its possible realizations. The other type of
nodes is defined as D
(i, j)
∈ D, where D
(i, j)
repre-
sents a discrete-valued random variable obtained us-
ing WMD and d
(i, j)
its possible realizations. Because
we have three WMD giving binary information for
each pixel, each node D
(i, j)
can take values from 0 to
7 (2
3
). In the table 1 the meaning of this values is
shown. Each node D
(i, j)
is related to each X
(i, j)
by
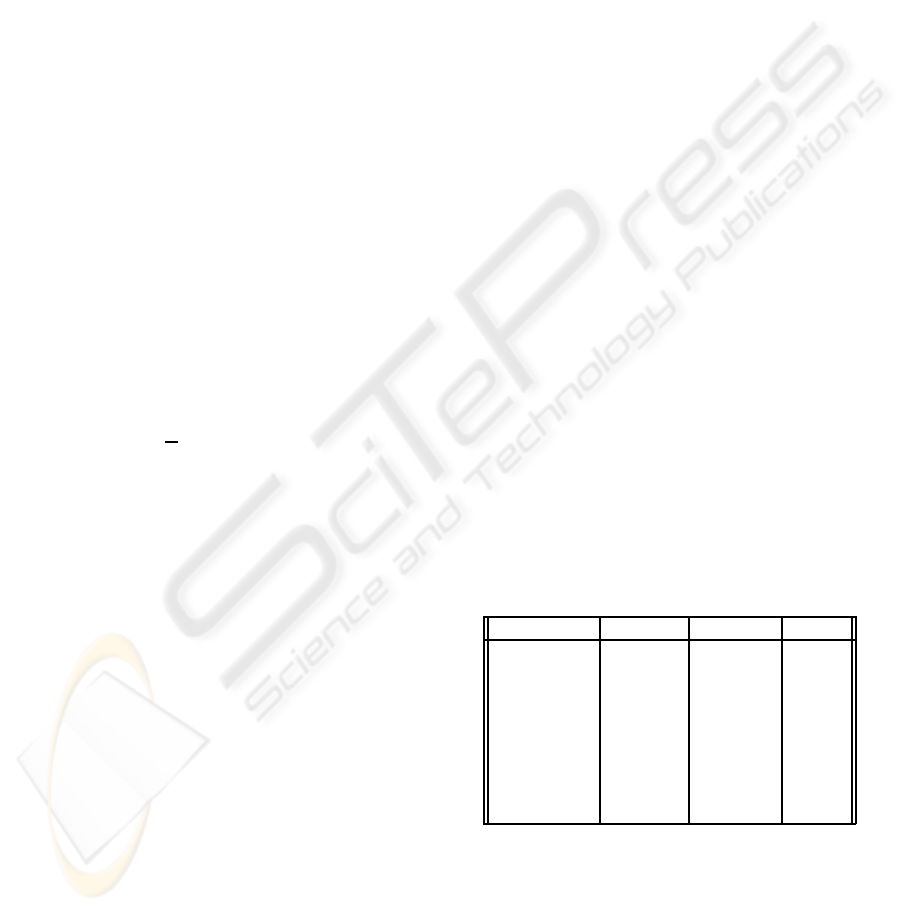
Table 1: Here are shown which detectors are activated to
produce the observation data value in the last column. D.
means Detector.
Shadow D. Edge D. Color D. Value
0
x 1
x 2
x x 3
x 4
x x 5
x x 6
x x x 7
a node factor h
(i, j)
∈ H which is the local evidence.
This relation is represented by two edges, one from
D
(i, j)
to h
(i, j)
and another from h
(i, j)
to X
(i, j)
.
We also have four relations between X
(i, j)
and its
neighborhood variable nodes X
(l,k)
where, (l, k) ∈
{(i− 1, j), (i+ 1, j), (i, j − 1), (i, j + 1)} , called com-
patibility function and denoted by f
<(i, j),(l,k)>
∈ F.
The relation with each neighbor is represented by two
MULTIPLE CUE DATA FUSION USING MARKOV RANDOM FIELDS FOR MOTION DETECTION
531

edges that forms the path from one node to the other
where between them there is the factor node.
In order to add temporal information, our model
has five layers that corresponds to five consecutive
frames from t − 2 to t + 2. To distinguish the nodes
in different temporal layer, we describe each node as
X
t
(i, j)
and each observation node as D
t
(i, j)
, where t rep-
resent the time index. This temporal information is
done by two relations with its neighborhood variable
nodes X
p
(i, j)
where, p ∈ {t − 1,t + 1}. This struc-
ture can be seen in figure 1. In order to simplify
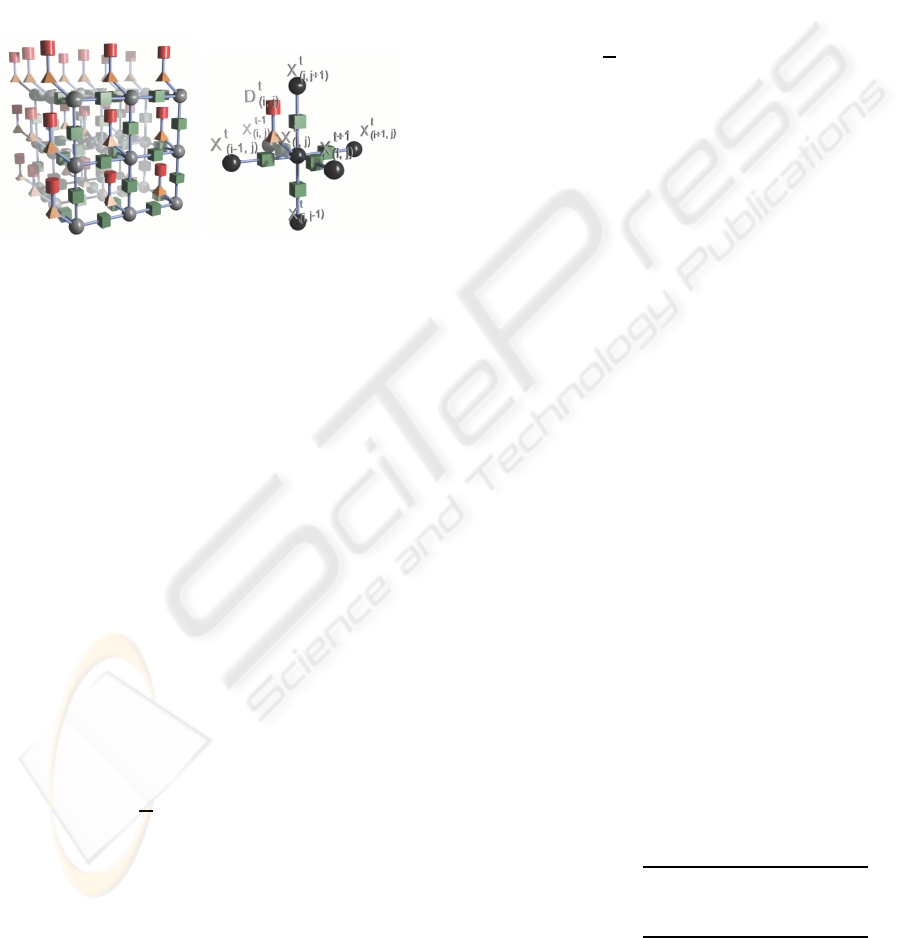
Figure 1: On the left we have a representation of our model
where spheres represents variable nodes from X, cylinders
represents variable nodes from D, cubes represents factors
from F and pyramids represents factors from H. On the right
we can see the connections of one node.
the notation let N be the total number of local evi-
dence functions and let h(x
n
, d
n
) be one of such func-
tions, where x
n
represents the possible realizations
of the corresponding variable node X
n
≡ X
t
(i, j)
∈ X
and d
n
the possible realizations of the correspond-
ing variable node D
n
≡ D
t
(i, j)
∈ D. Let be f(x
o
, x
u
)
one compatibility functions, where x
o
and x
u
, repre-
sents the possible realizations of the variable nodes
{X
o
, X
u
} ≡ {X
t
(i, j)
, X
p
(l,k)
} ∈ X that are neighbors.
And let be M the total number of compatibility func-
tions and f
m
(x
m
) one of this functions where, x
m
rep-
resent the possible realizations of two variable nodes
{X
t
(i, j)
, X
p
(l,k)
} ∈ X and is equivalent to f(x
o
, x
u
). For
this model the joint probability distribution is defined
as,
P(X
1
= x
1
, ..., X
N
= x
N
, D
1
= d
1
, ..., D
N
= d
N
) ≡ P(x, d)
(10)
P(x, d) =
1
Z
N
∏
n=1
h(x
n
, d
n
)
M
∏
m=1
f
m
(x
m
) (11)
Note that this join probabilitymass function is like the
MRF joint probability mass function but, adapted to
add the observationdata of our weak motion detectors
and simplified using binary compatibility functions.
Because the state for each variable node D
n
is
fixed by the observation data, we only want to infer
the optimal state for each variable node X
n
. The sum-
product adapted message equation for our model from
variable nodes X
n
to factor nodes f
m
is defined as,
q
n→m
(x
n
) = h(x
n
, d
n
)
∏
m
′
∈M(n)\m
r
m
′
→n
(x
n
) (12)
and messages r
m→n
from factor nodes f
m
to variable
nodes X
n
is defined as
r
m→n
(x
n
) =
∑
x
m
\n

f
m
(x
m
)
∏
n
′
∈N(m)\n
q
n
′
→m
(x
n
′
)

(13)
Finally the belief b
n
(x
n
) equation is defined as,
b
n
(x
n
) =
1
Z
h(x
n
, d
n
)
∏
m∈M(n)
r
m→n
(x
n
) (14)
or,
b
n
(x
n
) ∝ h(x
n
, d
n
)
∏
m∈M(n)
r
m→n
(x
n
) (15)
if we want to avoid the computation of the normaliza-
tion constant Z.
We define the local evidence h(x
n
, d
n
) as shown in
16 and the compatibility matrix f(x
o
, x
u
) as in 17.
h(x
n
, d
n
) =























[ϑ
0
, 1− ϑ
0
]
T
if D
n
= 0
[ϑ
1
, 1− ϑ
1
]
T
if D
n
= 1
[ϑ
2
, 1− ϑ
2
]
T
if D
n
= 2
[ϑ
3
, 1− ϑ
3
]
T
if D
n
= 3
[ϑ
4
, 1− ϑ
4
]
T
if D
n
= 4
[ϑ
5
, 1− ϑ
5
]
T
if D
n
= 5
[ϑ
6
, 1− ϑ
6
]
T
if D
n
= 6
[ϑ
7
, 1− ϑ
7
]
T
if D
n
= 7
(16)
f(x
o
, x
u
) =

θ if X
o
= X
u
1− θ otherwise
(17)
To obtain all the parameters in our algorithm ϑ
0,..,7
and θ we made a probabilistic study on our data us-
ing n representative frames (I
0,..,n−1
). We manually
annotated all the images of this set to obtain a set L
k
of matrices. Each L
k
is a binary matrix where not null
values represents foreground.
ϑ
a
= P(X
j
= 1|D
j
= a)
1− ϑ
a
= P(X
j
= 0|D
j
= a)
(18)
We can say that ϑ
a
is the prior probability of a
pixel annotated as a to belong to a dynamic pixel
(foreground). With this definition, we can use Bayes
Theorem to compute this probability.
P(X
j
= 1|D
j
= a) =
P(D
j
= a|X
j
= 1)P(X
j
= 1)
P(D
j
= a)
(19)
P(X
j
= 0|D
j
= a) =
P(D
j
= a|X
j
= 0)P(X
j
= 0)
P(D
j
= a)
(20)
Let m be the number of pixels in an image and D
k
i
the value of the observation data in the pixel i on the
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
532

frame k. We compute the marginals and the likelihood
using the annotated frames L
k
.
P(X
j
= 1) =
1
n· m
n−1
∑
k=0
m−1
∑
i=0
L
k
i
(21)
P(X
j
= 0) = 1− P(X
j
= 1) (22)
P(D
j
= a) =
1
n· m
n−1
∑
k=0
m−1
∑
i=0
Z
∞
−∞
δ(a− D
k
i
)dδ (23)
P(D
j
= a|X
j
= 1) =
∑
n−1
k=0
∑
m−1
i=0
L
k
i
R
∞
−∞
δ(a− D
k
i
)dδ
∑
n−1
k=0
∑
m−1
i=0
L
k
i
(24)
P(D
j
= a|X
j
= 0) = 1− P(D
j
= a|X
j
= 1) (25)
where δ is the delta function. Finally we can compute
θ as are shown in (26).
θ =
1
n· m
n−1
∑
k=0
m
∑
i=1
∑
l∈N(L
k
i
)
R
∞
−∞
δ(l − L
k
i
)dδ
N
k
i
(26)
Where N
k
i
and N(L
k
i
) is the number of neighbors and
the neighbors of L
k
i
.
5 EXPERIMENTAL RESULTS
In order to validate our approach we have compared
our method using a different number of iterations to
solve our MRF, different amount of temporal infor-
mation and different combinations of our weak mo-
tion detectors.
For the purpose of having a better comparative
we have applied these algorithms in different scenar-
ios. The videos were captured using the photo camera
Cannon Ixus 700 and recorded with QVGA and VGA
resolution at 30 fps. These videos have a lot of noise
due to the poor MPEG compression, that makes it dif-
ficult to obtain correct segmentation. The videos are
recorded on a bridge over a highway using two differ-
ent angles.
We also tested this algorithm, without the shadow
weak motion detector (our shadow detector needs a
RGB image) and with a version of our color weak
motion detector that works on gray scale images, on
a VGA IR video. These results are shown in figure
2. Our algorithm has been implemented using Mat-
lab R2008a and some parts using C++, like the maxi-
mization of the joint probability function of our MRF
using BP. This method doesn’t works in real time.
Needs 0.5 seconds to obtain all the data from the weak
classifiers and another 0.3 seconds to solve the MRF.
However we have not used threads (BP is highly par-
allelizable), the major part of the algorithm is wrote
Figure 2: Some results obtained using an IR Camera.
Figure 3: The graphics shows the percentage of pixel false
negatives and pixel false positives respect to the different
number of frames used for the temporal resolution.
in matlab and we do not used CUDA
1
. We estimate
that our computation time can be reduced by a factor
of ten.
In figure 3 we show the difference between using
different number of frames in our MRF (more tempo-
ral information). As shown, after ten frames, adding
more frames does not affect the results.
Figure 4 shows how the results vary depending on
the number of BP iterations. As shown, after 5 itera-
tions BP typically converges to a solution.
Figure 4: The graphics shows the percentage of pixel false
negatives and pixel false positives respect to the number of
BP iterations. At the bottom, we show the result using 1 and
5 iterations and its difference.
Figure 5 shows how the result of our method is
improved as the number of weak classifiers increases.
As expected, the addition of more information pro-
vides better results.
1
CUDA - Compute Unified Device Architecture.
MULTIPLE CUE DATA FUSION USING MARKOV RANDOM FIELDS FOR MOTION DETECTION
533

Figure 5: The top images are the results of the color WMD,
edge WMD and shadow WMD. The first bottom image is
the result using only the color information, the next image
uses color and edge information and the last one uses all the
information.
6 CONCLUSIONS
We have presented a new method to combine different
weak motion detectors in order to obtain a motion de-
tector that improves the results of the individual mo-
tion detectors. We also have shown how to model this
problem by using a MRF and how to solve it using
BP. The main problem of our approach is the selec-
tion of the weak motion detectors that aport the ob-
servation data into our system. It is not trivial to find
which WMD are a good choice for our system. An
interesting direction of our future work could be to
add a boosting-like method to obtain the best WMDs.
This could be easily incorporated to our framework
because the model is independent to the WMD and
the parameters of the joint probability function in our
MRF are found automatically just using the WMD
output.
ACKNOWLEDGEMENTS
This work was produced thanks to the support of the
Universitat Aut`onoma de Barcelona. Thanks are also
due to Tecnobit S.L. for providing the Infrared.
REFERENCES
Ahmed M. Elgammal, David Harwood, L. S. D. (2000).
Non-parametric model for background subtraction. In
Lecture Notes In Computer Science.
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning. Springer, London, 1rst edition.
Bohyung Han, Dorin Comaniciu, L. D. (2004). Sequential
kernel density approximation through mode propaga-
tion: Applications to background modeling. In Asian
Conference on Computer Vision (ACCV).
Desa, S. M. and Salih, Q. A. (2004). Image subtraction for
real time moving object extraction. In Proceedings of
the International Conference on Computer Graphics,
Imaging and Visualization (CGIV).
Felzenszwalb, P. F. and Huttenlocher, D. P. (2004). Efficient
belief propagation for early vision. In In CVPR.
J.C.MacKay, D. (2003). Information Theory, Inference, and
Learning Algorithms. Cambridge.
K. Toyama, J. Krumm, B. B. and Meyers, B. (1999).
Wallflower: Principles and practice of background
maintenance. In International Conference on Com-
puter Vision (ICCV).
Kindermann, R. and Snell, J. L. (1980). Markov Random
Fields and Their Applications. American Mathemati-
cal Society, 1rst edition.
Kohli, P. and Torr, P. H. S. (2005). Effciently solving dy-
namic markov random fields using graph cuts. In In-
ternational Conference on Computer Vision (ICCV).
Koller, D., Weber, J., and Malik, J. (1994). Robust multiple
car tracking with occlusion reasoning. In European
Conference on Computer Vision (ECCV).
Lo, B. and Velastin, S. (2000). Automatic congestion de-
tection system for underground platforms. In Proc.
of 2001 Int. Symp. on Intell. Multimedia, Video and
Speech Processing.
N.M. Oliver, B. R. and Pentland, A. (2000). A bayesian
computer vision system for modeling human interac-
tions. In Pattern Analysis and Machine Intelligence
(PAMI).
Qian, R. J. and Huang, T. S. (1997). Object detection using
hierarchical mrf and map estimation. In CVPR 1997,
Conference on Computer Vision and Pattern Recogni-
tion.
R. Cucchiara, C. Grana, M. P. and Prati, A. (2003). De-
tecting moving objects, ghosts and shadows in video
streams. In Pattern Analysis and Machine Intelligence
(PAMI).
Rittscher, J., Kato, J., Joga, S., and Blake, A. (2000). A
probabilistic background model for tracking. In Inter-
national Conference on Computer Vision (ICCV).
Stauffer, C. and Grimson, W. E. L. (1999). Adaptive back-
ground mixture models for real-time tracking. In
Computer Vision and Pattern Recognition (CVPR).
Wang, D., Feng, T., yeung Shum, H., and Ma, S. (2002). A
novel probability model for background maintenance
and subtraction. In In Int. Conf. on Vision Interface.
Weiss, Y. and Freeman, W. T. (2001). Correctness of belief
propagation in gaussian graphical models of arbitrary
topology. In Neural Computation.
Yedidia, J. S., Freeman, W. T., and Weiss, Y. (2005). Con-
structing free energy approximations and generalized
belief propagation algorithms. In IEEE Transactions
on Information Theory.
Yin, Z. and Collins, R. T. (2007). Belief propagation in a
3d spatio-temporal mrf for moving object detection.
In CVPR 2007, Conference on Computer Vision and
Pattern Recognition.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
534