A NEW NON-REDUNDANT SCALE INVARIANT INTEREST POINT

DETECTOR

Luis Ferraz

Department of Computing Science, Universitat Autonoma de Barcelona, Barcelona, Spain

Xavier Binefa

Department of Information and Communication Technologies, Universitat Pompeu Fabra, Barcelona, Spain

Keywords:

Interest points extraction, Gaussian curvature, Scale space.

Abstract:

In this paper we present a novel scale invariant interest point detector of blobs which incorporates the idea of

blob movement along the scales. This trajectory of the blobs through the scale space is shown to be valuable

information in order to estimate the most stable locations and scales of the interest points. Our detector

evaluates interest points in terms of their self trajectory along the scales and its evolution avoiding redundant

detections. Moreover, in this paper we present a differential geometry view to understand how interest points

can be detected. We propose analyze the gaussian curvature to classify image regions as elliptical (blobs) or

hyperbolic (corners or saddles).

Our interest point detector has been compared with Harris-Laplace and Hessian-Laplace detectors on infrared

(IR) images, outperforming their results in terms of the number and precision of interest points detected.

1 INTRODUCTION

Interest point detection algorithms have been shown

to be well suited for feature extraction. The main goal

of these algorithms is to allow the extraction of fea-

tures invariant to some viewing conditions. Scale in-

variant detectors estimate the location and the scale of

these features. Different scale invariant detectors have

been developed over the past few years and among

the most important we can ﬁnd Laplacian of Gaus-

sian (LoG) (Lindeberg, 1998), Derivative of Gaus-

sian (DoG) (Lowe, 2004), Harris-Laplace (Mikola-

jczyk and Schmid, 2004), Hessian-Laplace (Mikola-

jczyk et al., 2005) or Maximally Stable Extremal Re-

gions (MSER) (Matas et al., 2002).

MSER produces good results in comparison with

other detectors but it is not analyzed in this paper

because of its bad performance on blurred images

(Mikolajczyk et al., 2005).

Typically, these detectors are based on a multi-

scale analysis of the image (Crowley, 1982). The

space-scale can be built using different scale normal-

ized operators, like Laplace ﬁlters or difference of

Gaussians ﬁlters. For these detectors an interest point

is detected if a local 3D extreme is present and if its

absolute value is higher than a threshold. Therefore,

blobs at different scales are not related and the same

blob can be detected many times along the scale-

space. To avoid this problem, our proposal is to es-

timate the trajectory of blobs along scales and select

the scale and location that best represent each blob.

From a differential geometry point of view im-

ages can be understood as surfaces with 3 types of

regions in function of their gaussian curvature: ellipti-

cal regions, parabolic regions and hyperbolic regions.

These types of regions allow to see images in a sim-

ple way, where elliptical regions can be understood as

blobs, parabolic regions as contours or plane regions

and hyperbolic regions as corners or saddles.

In order to extract this differential structure we use

the full Hessian matrix (DoCarmo, 1976) for each

point. This approach outperforms Laplacian based

operators more related to obtain rotational invariant

information (Lenz, 1992).

This paper is organized as follows. In section 2 the

method to detect interest points by means of curvature

analysis is introduced. In section 3 our scale invariant

interest point detector is described and ﬁnally, in Sec-

tion 4 we present experimental results.

277

Ferraz L. and Binefa X. (2009).

A NEW NON-REDUNDANT SCALE INVARIANT INTEREST POINT DETECTOR.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 277-280

DOI: 10.5220/0001802702770280

 SciTePress

2 CURVATURE ANALYSIS

The image behaviorin a local neighborhood of a point

can be obtained by the second order Taylor ap-

proach,

f(~x) = f(~x

) + ∇f(~x

)(~x− ~x

) (1)

∇

f(~x

)(~x− ~x

)

+ R(~x)

where the second term contains information about

the gradient distribution in a local neighborhood. Us-

ing this gradient informationcan be computed the ﬁrst

fundamental form I (Equation 2). The next term is the

second fundamental form II (Equation 3) that con-

tains information about the shape near to x

. The last

term R(x) is referred to as the remainder, since it con-

tains the difference between the image f(~x) and its

representation.

I(~x

,σ) =



1+ f

(~x

,σ) f

(~x

,σ)

(~x

,σ) 1+ f

(~x

,σ)



(2)

II(~x

,σ) =



(~x

,σ) f

(~x

,σ)

(~x

,σ) f

(~x

,σ)



(3)

where σ is the scale normalization factor for the

space-scale.

The ﬁrst and second fundamental forms of a sur-

face determine an important differential-geometricin-

variant, the Gaussian curvature K. The Gaussian cur-

vature of a point on a surface is the product of the

principal curvatures, K = k

∗ k

of the given point.

Moreover, Gaussian curvature can be expressed as the

ratio of the determinants of the second and ﬁrst fun-

damental forms,

K =

det(II)

det(I)

(4)

The sign of the Gaussian curvature at a point de-

termines the shape of the surface near that point (Do-

Carmo, 1976): for K > 0 the surface is locally convex

(blob regions) and the point is called elliptic, while for

K < 0 the surface is saddle shaped (i.e. corners) and

the point is called hyperbolic. The points at which the

Gaussian curvature is zero (i.e. contours) are called

parabolic.

The ﬁrst fundamental form is positive deﬁnite,

hence its determinant is positive everywhere. There-

fore, the sign of K coincides with the sign of the de-

terminant of the second fundamental form. Assuming

that point ~x

is a critical point (the gradient ∇f(~x

)

vanishes) the Gaussian curvature of the surface at ~x

is the determinant of II(~x

). So, it is not necessary to

calculate I(x

) to estimate the Gaussian curvature.

Figure 1: Saddle surface with normal planes in directions

of principal curvatures.

In Figure 1 is shown the meaning of curvature.

Given the normal vector to the point ~x

, its tangent

plane and its two principal curvatures k

and k

Gaus-

sian curvature is deﬁned positive if both curvatures

have the same sign, negative if they have different

sign and zero if any curvature is zero.

3 OUR INTEREST POINT

DETECTOR OF BLOBS

In this section we propose a new scale invariant in-

terest point detector of blobs based on the analysis of

Gaussian curvature of the image along the space-scale

representation. Moreover, to obtain more stable inter-

est points the trajectory of each one is extracted.

The evolution of blobs along scales was studied in

depth by (Lindeberg, 1993). Traditionally, the anal-

ysis of the behavior of blobs presents severe compli-

cations, since it implied a detailed description of the

image. However, for our purposes we do not need

a precise description and one of the important con-

tributions of our work is to reduce the detail of the

analysis since we only need an approximation of the

movement of blobs.

Figure 2: Trajectory of some blobs along scales (blue lines).

Blob movements and blob fusions can be seen. Green points

show all the extremes found. Red points are the extremes

selected as interest points.

To obtain this approximation, in ﬁrst place a

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

278

space-scale representation must be build. Scale nor-

malized second fundamental form (Equation 3) is

used in order to obtain it calculating the Gaussian cur-

vature K associated to each point of each scale.

All the maxima are computed for each scale to

ﬁnd all the blobs. Once obtained, they must be an-

alyzed to put them in correspondence. Blobs found in

consecutive scales are linked using a gradient ascent

propagation algorithm to ﬁnd the nearest and plausi-

ble link. As a result of this step, the pipe/trajectory of

each blob is obtained. Experimentally, we have seen

that using this simple strategy provides a coherent and

good approximation of the trajectories.

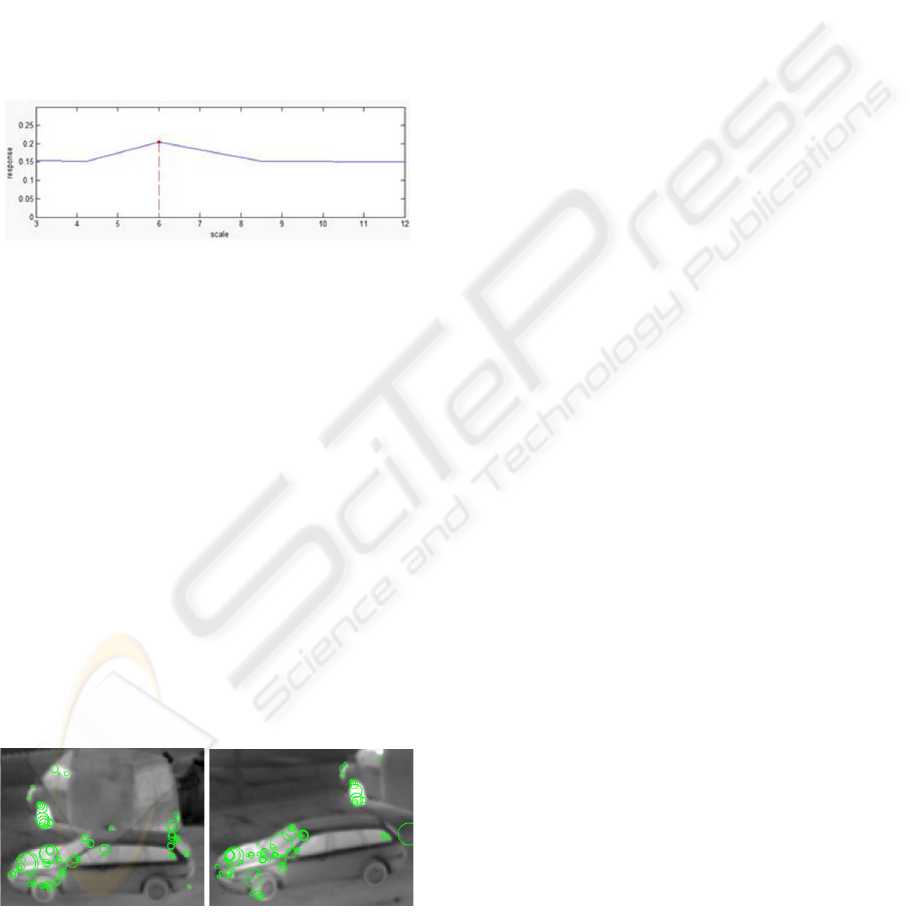
Figure 3: Example of values for the Gaussian curvature

along scales given one blob trajectory.

The last step consists on obtaining from each blob

trajectory which are those locations that maximize

their Gaussian curvature compared with their nearest

neighbors in the pipe (Figure 3).

4 EXPERIMENTAL RESULTS

IR images are thermal images that contain a high sig-

nal to noise ratio and a lack of contrast, so blurred

images are obtained. We have compared our method

with two typical interest point detectors that have

proved, accordingly to literature, that produce good

results: Harris-Laplace and Hessian-Laplace. The

ﬁrst one is based on the detection of corners that are

representative along the space-scale and the second

one on the detection of blobs.

Figure 4: Example of interest points detected using Harris-

Laplace detector (green circles symbolize location and

scale) on two different images of an IR sequence. Com-

paring detected points on the images is shown that interest

points are unstable.

Harris-Laplace detector calculates corners at the

different scales using a scale adapted Harris opera-

tor. After that, locations of detected corners are eval-

uated with a Laplacian ﬁlter in the superior and infe-

rior scales. Interest points correspond to corners with

a maximal response of Laplacian ﬁlter.

Harris-Laplace detector has been applied on IR

images to test its performance on these images. As

Harris-Laplace detector is based on Harris operator

and therefore, since in IR images corners are not

sharpened, it produces bad results in contrast with

Hessian-Laplace. Figure 4 show that Harris-Laplace

detector produces unstable interest points in IR im-

ages. Therefore, the same object viewed from differ-

ent points of view produces interest points in different

locations and scales. Moreover, Figure 4 shows that

the same interest point is detected in different scales

using this detector.

Hessian-Laplace detector works in a similar way

to Harris-Laplace detector(Mikolajczyk et al., 2005).

The main difference is that instead of Harris opera-

tor uses a function based on the determinant of the

Hessian matrix to penalize very long structures (for

example it is useful to discard contours detected as

blobs).

Given that Harris-Laplace produces unstable re-

sults the ﬁnal comparison has been done between

Hessian-Laplace detector and our blob detector.

These two detectors are based on the detection of

blobs, differing in two ways: the method to decide

which neighbors around extremes must be analyzed

and the function applied to extreme detection.

Comparing Hessian-Laplace and our detector is

where the power of our algorithm is shown in a best

way. Figure 5 compare these two algorithms show-

ing that Hessian-Laplace detects a high quantity of

interest points being the most of them redundant. Our

detector practically does not produce redundancy be-

cause of trajectory of blobs gives information about

the best scale. Moreover, our detector seems to ﬁnd

interest points closest to our perception that the other

one.

5 CONCLUSIONS

We have presented a powerful mechanism to detect

the most stable locations of blobs by estimating their

trajectory along scales. By means of this trajectory

the best locations and scales for each point can easily

be selected. Moreover, by using the Gaussian curva-

ture we classify regions on images in a simple way.

We have shown that over IR images those inter-

est point detectors based on corner detection do not

A NEW NON-REDUNDANT SCALE INVARIANT INTEREST POINT DETECTOR

279

(a) (b)

(e) (f)

(g) (h)

Figure 5: Hessian-Laplace versus our detector. (a), (c), (e)

and (g) show the Hessian-Laplace results over 4 IR images.

(b), (d), (f) and (h) show the results of our detector over the

same 4 IR images. Red circles symbolize the locations and

scales of interest points.

produce satisfactory results, due to the lack of sharp-

ness of the contours. It is also a fact that interest point

detectors based on blob detection, although they pro-

duce good results, most of them are redundant.

By comparing these blob detectors with our pro-

posed detector we show that our algorithm works ﬁne,

producing promising results. It also opens future re-

search lines around blob trajectories along scales and

Gaussian curvature analysis using ﬁrst and second

fundamental forms. Moreover, an extension to the

detection of afﬁne blobs could be done by analyz-

ing in depth the Gaussian curvature surface generated

around each interest point.

Finally, we want to remark that our detector has

been tested mainly on IR images. However, tests done

on gray level images have produced similar results.

ACKNOWLEDGEMENTS

This work was produced thanks to the support of the

Universitat Aut`onoma de Barcelona. Thanks are also

due to Tecnobit S.L. for yielding the car sequence im-

ages.

REFERENCES

Crowley, J. L. (1982). A representation for visual informa-

tion with application to machine vision. PhD thesis.

DoCarmo, M. P. (1976). Differential Geometry of Curves

and Surfaces. Prentice-Hall.

Lenz, R. (1992). Group theoretical feature extraction:

Weighted invariance and textulre analysis. In The-

ory & Applications of Image Analysis: Selected Pa-

pers from the 7th Scandinavian Conference on Image

Analysis, pages 63–70.

Lindeberg, T. (1993). Scale-Space Theory in Computer

Vision (The International Series in Engineering and

Computer Science). Springer.

Lindeberg, T. (1998). Feature detection with automatic

scale selection. International Journal of Computer Vi-

sion, 30:77–116.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60:91–110.

Matas, J., Chum, O., Urban, M., and Pajdla, T. (2002). Ro-

bust wide baseline stereo from maximally stable ex-

tremal regions. In In British Machine Vision Confer-

ence, pages 384–393.

Mikolajczyk, K. and Schmid, C. (2004). Scale & afﬁne in-

variant interest point detectors. International Journal

of Computer Vision, 60:63–86.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Van Gool,

L. (2005). A comparison of afﬁne region detectors.

International Journal of Computer Vision, 65:43–72.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

280