SCALE ROBUST ADAPTIVE FEATURE DENSITY

APPROXIMATION FOR VISUAL OBJECT

REPRESENTATION AND TRACKING

C. Y. Liu, N. H. C. Yung

Laboratory for Intelligent Transportation Systems Research, Department of Electrical & Electronic Engineering

The University of Hong Kong, Pokfulam Road, Hong Kong SAR, China

R. G. Fang

Information Science & Engineering College, Zhejinang University, No.8 Zheda Road, Hangzhou, Zhejiang, China

Keywords: Tracking, Feature Scale Selection, Density Approximation, Bayesian Adaptation, MAP, EM.

Abstract: Feature density approximation (FDA) based visual object appearance representation is emerging as an

effective method for object tracking, but its challenges come from object’s complex motion (e.g. scaling,

rotation) and the consequent object’s appearance variation. The traditional adaptive FDA methods extract

features in fixed scales ignoring the object’s scale variation, and update FDA by sequential Maximum

Likelihood estimation, which lacks robustness for sparse data. In this paper, to solve the above challenges, a

robust multi-scale adaptive FDA object representation method is proposed for tracking, and its robust FDA

updating method is provided. This FDA achieve robustness by extracting features in the selected scale and

estimating feature density using a new likelihood function defined both by feature set and the feature’s

effectiveness probability. In FDA updating, robustness is achieved updating FDA in a Bayesian way by

MAP-EM algorithm using density prior knowledge extracted from historical density. Object complex

motion (e.g. scaling and rotation) is solved by correlating object appearance with its spatial alignment.

Experimental results show that this method is efficient for complex motion, and robust in adapting the

object appearance variation caused by changing scale, illumination, pose and viewing angel.

1 INTRODUCTION

Visual object tracking is widely demanded in traffic

management, pedestrian monitoring, and security

inspection. The challenge of visual object tracking is

that the changing illumination, changing object’s

pose, changing viewing angel and partial occlusion

will all change the object’s scale, size and visible

parts. Thus the low-level image features can not be

constantly detected across frames without variations,

as the feature probability density function (pdf) of

the object does not rely on every exact local feature

the methods representing an object’s as its pdf

approximations by feature density approximations

(FDA) have emerged as a effective object

representation for tracking. Those can be divided

into the two groups: parametric approximation and

non-parametric approximation. The parametric

approximation methods (e.g. Raja, Yu, Jepson et al)

used a Gaussian Mixture Model (GMM) to

approximate the object’s feature density and

Expectation-Maximization (Dempster et al) (EM) to

estimate the GMM parameters. To adapt to object’s

changing appearance, Raja et al update estimate

Maximum likelihood (ML) GMM parameter online

recursively. However, it is not able to cope with

complex motion (e.g. rotation and scaling) because

there’s no spatial information in their model. Yu &

Wu attempted to resolve this issue by extending

feature vector by pixel coordinates and track object

in an ML estimation process by EM algorithm.

Jepson et al developed a three components mixture

model to represent object appearance. They used

online ML estimation to update the model

parameters, but it’s not robust when observed data

are sparse (object moving in decreasing scale or

resolution). For non-parametric FDA methods,

Comaniciu et al used spatially weighted kernel

functions to represent target object and use mean-

shift to determine the kernels. Han et al proposal to

535

Liu C., Yung N. and G. Fang R. (2009).

SCALE ROBUST ADAPTIVE FEATURE DENSITY APPROXIMATION FOR VISUAL OBJECT REPRESENTATION AND TRACKING.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 535-540

DOI: 10.5220/0001802805350540

 SciTePress

use On-line learning to update kernel density to

adapt to object’s appearance variation. However, as

pointed by Carreira-Perpinan, the kernel density

derived by meanshift developed by Comaniciu et al

in the above methods is the ML estimation; it is not

capable in providing a robust estimate with sparse

data.

In this paper, to solve the above limitations, we

propose a robust multi-scale adaptive feature density

approximation (FDA) object representation method

for tracking, and provide its robust Bayesian

updating method using density’s prior knowledge

from historical frames. We also solve object

complex motion by correlating object appearance

with its spatial alignment. Experiment result shows

the effectiveness of this method.

This paper is organized as follow: in Section 2

we introduce the object representation for tracking,

and robust representation updating method; in

Section 3 the experiment and results are presented

and discussed; and the paper is concluded in Section

2 ROBUST FDA FOR OBJECT

REPRESENTAION AND MAP

FDA UPDATING

In the proposed object representation method, scale

robustness is achieved in both feature extraction and

density estimation. The image features are extracted

from image patches in the selected scale and size

according to local image pattern. and the effective

probability for the features from each patch is

defined by the size of the patch. Using a new

likelihood function defined by the feature sets and

their effective probability, the Feature density is

estimated robustly to object changing scale. Based

on this representation, we also proposal how to

measure the compatibility between feature set and its

density representation for object tracking. To adapt

to an object’s changing appearance, we provide the

MAP-EM updating FDA updating method using the

density’s conjugate priors to transfer priori

knowledge in historical frames to current estimation

in a Bayesian way. To cope with object complex

motion (e.g. rotation and scaling) we correlate object

appearance with the appearance’s spatial alignment

by extend feature with spatial coordinates in the

coordinate system of the object itself. The following

gives the detail description for our method.

2.1 Scale Robust Reature Extraction

In our method, scale robust FDA is achieved in both

the stages of feature extraction and feature density

estimation. As image feature appears in its own scale

and size, the robust features should be extracted

accordingly. As in our previously works by Liu &

Yung, the method partition a frame into multi-scale

patches w.r.t. the scale and size of local feature, and

extract features on these patches. The process for

feature extraction is depicted in Fig. 1, a result is

demonstrated in Fig. 2.

Figure 1: Robust feature extraction.

This figure depicts the process of scale-robust feature extraction.

Diagram A describes the data flow in this process; diagram describes

how a frame is partitioned into multi-scale patches. Here Lindeberg’s

multi-scale decomposition is used; as suggest by Timor et al, patches’

scale and size are select by comparing entropy across scale.

After frame partition, an effective

probability

creb

for each patch is defined on the

number of pixels in the patch, to control the

contribution of each patch’s feature in FDA.

creb

defined as:

max

creb

Size Size=

(1)

To solve complex motion (e.g. rotation, scaling), the

model should acknowledge the object’s pose. This is

achieved through correlating the object appearance

feature with its spatial alignment by extending the

features’ dimension with the coordinate of patches’

geometry centre in the coordinate system of the

object itself (As depicted in Fig. 3) The

transformation between the coordinate system of the

object

(,)

and the coordinate system of original

frame

(, )

is:

cos sin

(, )( , )[ ]

sin cos

xy xmym

=− −

−

(2)

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

536

where

(,)

is the center of the object,

is the

rotation angel of object.

Figure 2: Multi-scale patches after image partition.

Image 1 is the original image; image 2 is the partition result. It should

be noted that the singularity regions are split into small patches in the

fine scale. In the homogeneous regions, large patches in a coarse scale

are retained. Image 3 is the final entropy map of each patch.

Figure 3: Coordinate system of the frame (blue) and.

coordinate system the object (green).

2.2 Robust Feature Density

Approximation

In this paper we approximate the object’s feature

density by a Gaussian Mixture Model:

( | ) ( | ; ); { ; }; { , },

ijijjjjjjj

Ω= Ω= =

∑

x ω x ωθωθμΣ

(3)

where

is its mixing coefficient,

1/2

1/2 1

(|;)(2) exp{()()}

ijj j j j

θπ

−

−−

=∑−−∑−x ω x μ x μ

is a

Gaussian component.

The robust FDA should be robust to both

object’s scale variation and the consequent variation

in image partition. As the features of large patches

correspond to the statistics of more pixels, they will

contribute more in FDA than the feature from

smaller patches. Therefore, a new likelihood

function defined by both the feature observations

and their effective probability, is used in GMM

estimation. The likelihood function is defined as:

(;) log (,;)

log [ ( | 1; ) ( 1) ]

[log ( | 1; ) log ( )],

creb

iij ij i

creb

ij i i ij j

Pz Pz P

zP P z P

Ω=

===

==+

∏

∏∏

∑∑

Xxzθ

x θ

(4)

where

is hidden variable indicating

is generated

by which one of the GMM components. Using

()l

in eq. (4), the Maximum Likelihood estimated

for GMM can be computed by EM algorithm:

}

)()(

exp{)(

}

)()(

exp{)(

],|[

∑

−

−∑−−

∑

−∑−−

∑

−

iijij

xzEh

tep

μxμx

(5)

()

()()

creb creb

jiji i

kcrebcreb

jijii iji

kkTcreb

ijij ij i

creb

ij i

Mstep

phPP

hP hP

−

−−

∑=

∑∑

∑

μ x

x μ x μ

(6)

Fig. 4 compares effectiveness of the new

likelihood for FDA with conventional method which

doesn’t consider the relationship between the size of

the patch and the contribution of its feature in the

FDA. Our method solves the problem in

conventional method.

Based on this FDA object representation, our

method provides measure for tracking by measuring

the compatibility of an image region’s feature set to

a GMM by:

(|) { }

where exp{ ( ) ( )}

creb

jj i

creb T

ji ijjij

PX P

ωφ

=∈

−

∈

Ω=

=−−−

∑∑

∑

x μΣx μ

(7)

Figure 4: Comparison of FDA in simulation image.

In Figure 4, image 1 is the original image, image 2 is the image

histogram, and image 3 is the histogram estimated by conventional

method; whereas image 4 is the estimation by the proposed method. The

proposed method produces an accurate estimation.

SCALE ROBUST ADAPTIVE FEATURE DENSITY APPROXIMATION FOR VISUAL OBJECT REPRESENTATION

AND TRACKING

537

2.3 MAP-EM Updating

As object appearance change with changing

illumination, scale, pose, and viewing angel, its

GMM appearance representation thus should be

updated to adapt its changing appearance. As

compared by Gauvain et al and Goldberger et al,

MAP estimation can be more robust the ML for

sparse data (i.e. the feature set) because it utilize the

prior knowledge of the model parameter.

We improve the robustness of model updating

for sparse date by using the model prior knowledge

in GMM conjugate priors (ref. Gamerman) and

update GMM by its MAP estimate in a Bayesian

way. To achieve scale robustness we also use the

new likelihood function in e.q.(4). We derived the

updating methods using MAP-EM algorithm. MAP

estimation estimate the by maximizing the a

posteriori probability

() (;)()

MAP

pΩ= Ω ΩX

thus

is estimated by:

argmax{ ( ; ) ( )}p

Ω= Ω ΩX

(8)

The conjugate prior for the GMM is:

1/2 1 1 1

0 0

() ( ) ( , )

(2 )

(, ) | | exp[ ( ) ( ) ( )]

jjj j j j j j j jj

pD g

ctr

αη

−

−−−

⎧⎫

⎪⎪

=×

⎨⎬

⎪⎪

⎩⎭

⎧⎫

⎪⎪

−− −−

⎨⎬

⎪⎪

⎩⎭

∏

θω| αμΣ

ΣΣ μm Σμm ΣΣ

(9)

where

()D ω

is the Dirichlet density distribution

for mixing coefficients, and

is its parameter.

For the mean vector and the precision matrix (the

inverse of covariance matrix) in each GMM

Gaussian component, their conjugate priors are the

normal distribution and the Wishart distribution. As

suggested in Goldberger et al, give the

parameters

(,, ), 1...

jj j

μΣ

of the GMM of last

time step, the parameters of the GMM conjugate

prior at the current time step can be extracted as:

constant,

,1,

jjjjjj

jj j j

ηω η

ηαηω

===

=+ = +

ΣΣ

(10)

Based on the conjugate prior and the new likelihood

function, the auxiliary function for MAP estimation

becomes:

'''

(|)log [(| 1;)( 1)]

log ( ) log ( , )

creb

iij

iij ij

QPzPz

===

∏∏

∏

θθ x θ

ω | αμΣ

(11)

Therefore we obtained the MAP-EM GMM

updating method as:

(, )

[|,] ,

(, )

jjj

ij ij i

jjj

Estep

hEzx

−

∑

μΣ

(12)

()()()()

creb

ij i j

creb

ij i

creb

ij i i j j

creb

ij i j

creb T T

iji ijij jjjjj jj

creb

ij i j

MStep

ηηω

ηω

ηη

−

−−+− −+

∑=

∑

x μ

μμ

m Σ

(13)

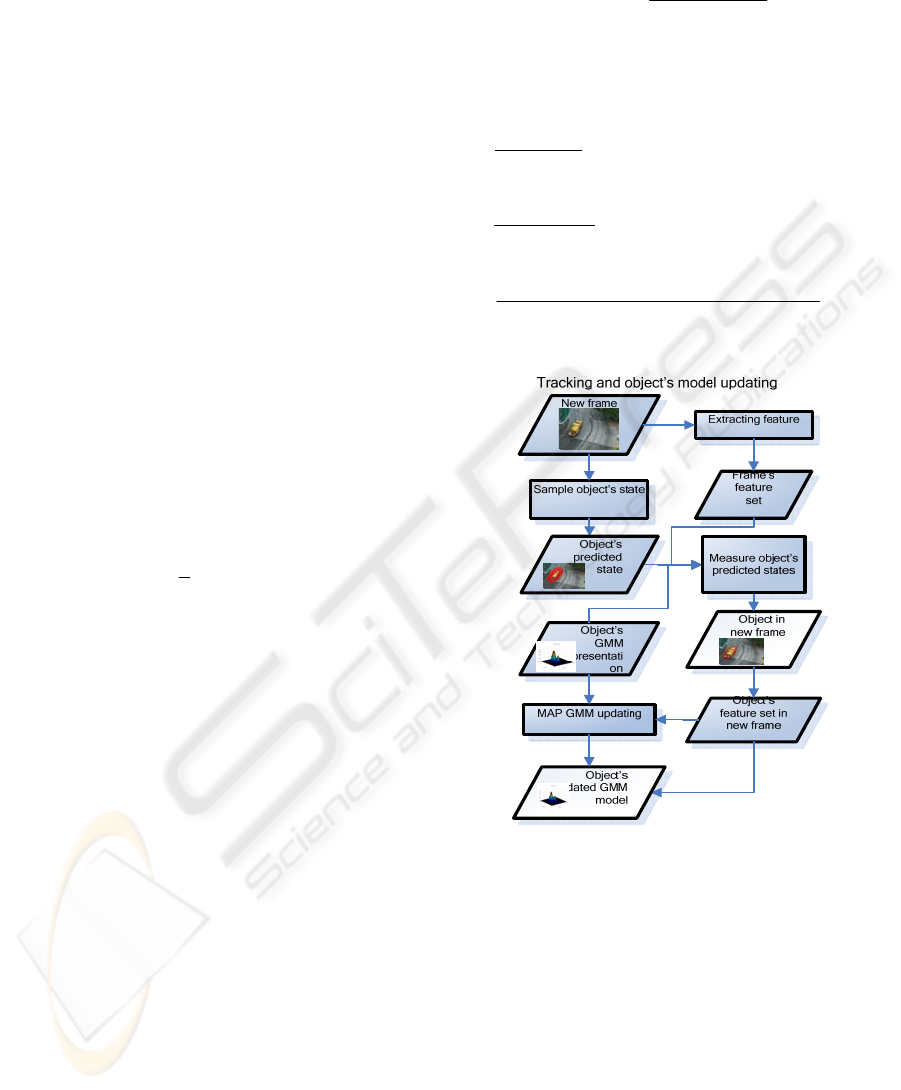
Figure 5: Object tracking and FDA model updating.

3 EXPERIMENTAL RESULTS

In the experiment, patches’ average value in Lab

colour space and centre coordinate are used as the

image feature vector; besides small patches, the

effectiveness of the non-homogeneous patches’

features are also tuned down according to entropy.

The state of the object is denoted as:

(, ,,)TT

where

,,,,TT

are the x, y

translation, rotation, and scaling of the object. The

object appearance is initialized using eq.(5), eq.(6);

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

538

Figure 6: Tracking with complex motion and scale variation.

Figure 7: Tracking with complex motion, scale/pose/illumination/appearance variation.

Figure 8: Tracking with appearance variation caused by changing illumination, changing pose, and changing scale.

then visual object is tracked by estimate the optimal

object state using the measurement form the

proposed FDA appearance representation in a

particle filter (Arulampalam et al) framework.

Specifically, the posterior probability of

approximated by a set of weighted discrete

particles

() () ()

{, }, 1

jjN j

iij i

∑

, and its MAP estimate

is obtained by choosing the particle with the largest

weight. The posterior probability are recursively

updated by predict new particles and measure their

weights by eq.(7) with GMM and the feature set in

image region corresponding to each particle. I.e., the

predicted particle is sampled from:

()

1: 1 1 1

(| ) (| )

ii ii i

−−−

∑

sy st

, and their weights measured

by:

()

(| ) ( |)

( | ) { }

iiiii

creb

jj i

wp p

PX P

ωφ

=∈

=Ω=

∑∑

ty yt

(14)

where and

is feature set in the image region of

particle

t . In model updating the GMM prior

knowledge is extracted form the last frame by

eq.(10), and the MAP-EM method in eq.(12),

eq.(13) is used for GMM updating.

Three experiments are given in Fig. 6~Fig.8. In

Fig. 6, the vehicle moves in decreasing scale and

change its pose by steering anti-clock wise. The

proposed method accurately tracks it with correct

scaling and rotation estimate, and capture its pose

SCALE ROBUST ADAPTIVE FEATURE DENSITY APPROXIMATION FOR VISUAL OBJECT REPRESENTATION

AND TRACKING

539

precisely even part of the object has moved out of

the image. In Fig. 7 & Fig. 8, tracking with

significant object appearance variation is tested. In

the two experiments, vehicles’ visible parts change

with its changing steering angel and view point; and

the shadow in Fig. 7 and highlight in Fig. 8 were

cast onto the vehicles when they move into the upper

part, they all bring significant appearance variations

to vehicles. The feature set for GMM updating

becomes sparse as the number of patches decreases

with vehicle’s decreasing scale. But in both

experiments the proposed method tracks the vehicle

accurately with correct pose (scaling & rotation)

estimate.

4 CONCLUSIONS

In this paper, to solve the above limitations in FDA

based object representation method in tracking, we

propose a robust multi-scale FDA object

representation method for tracking, and provide the

robust FDA updating method. Scale robustness is

achieved by both robust feature extraction and

robust density estimation. The Bayesian model

updating method is proposed using model prior

knowledge extracted from historical model.

Experiment shows the effectiveness of the method.

Our future directions could include explorations to

different features and tracking by multiple feature

fusion. Finally the aim is to develop it to a multiple

interacting objects tracking method.

REFERENCES

Arulampalam M. S., Maskell S., Gordon N., Clapp T.,

2002. “A tutorial on particle filters for online

nonlinear/non-Gaussian Bayesian tracking”. IEEE

Transactions on Signal Processing, Vol. 50(2),

pp.174-188.

Carreira-Perpinan M.A., 2007. “Gaussian Mean-Shift Is an

EM Algorithm”. IEEE Transactions on Pattern

Analysis and Machine Intelligence, Vol. 29(5), pp.767

– 776.

Comaniciu D., Meer P., 2002. “Mean Shift: A Robust

Approach toward Feature Space Analysis”, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. 24(5), pp. 603-619.

Comaniciu D., Ramesh V., Meer P., 2003. “Kernel based

object tracking”. IEEE Transactions on Pattern

Analysis and Machine Intelligence, Vol. 25(5), pp. 564

– 577.

Dempster A. P., Laird N. M., Rubin D. B., 1977.

"Maximum Likelihood from Incomplete Data via the

EM Algorithm". Journal of the Royal Statistical

Society, Series B, Vol. 39, No. 1, pp.1-38.

Gamerman D., 1997. “Markov chain Monte Carlo:

stochastic simulation for Bayesian inference”.

CHAPMAN & HALL/CRC.

Gauvain J. L., Lee C.H., 1994. “Maximum a Posteriori

Estimation for Multivariate Gaussian Mixture

Observations of Markov Chains”. IEEE Transactions

on Speech and Audio Processing, 2(2):291-298.

Goldberger J., Greenspan H., 2006. “Context-based

segmentation of image sequences”. IEEE Transactions

on Pattern Analysis and Machine Intelligence, Vol.

28(3), pp. 463 – 468.

Han B., Comaniciu D., Zhu Y., Davis L., 2008.

“Sequential Kernel Density Approximation and Its

Application to Real-Time Visual Tracking”. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. 30(7), pp. 1186 – 1197.

Jepson A. D., D. Fleet J., El-Maraghi T. F., 2003. “Robust

online appearance models for visual tracking”. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. 25(10), pp.1296- 1311.

Lindeberg T., 1994. “Scale-Space Theory in Computer

Vision”. Kluwer Academic Publishers, Dordrecht, the

Netherlands.

Liu C.Y., Yung N.H.C., 2008. “Multi-scale feature density

approximation for object representation and tracking”.

IASTED Signal Processing, Pattern Recognition and

Applications.

Raja Y., Mckenna S. J., Gong S., 1999. “Tracking color

objects using adaptive mixture models”. Image and

Vision Computing, Vol. 17(3-4), pp.225–231.

Timor K., Michael B.

，2001. “Saliency, Scale and Image

Description”, International Journal of Computer

Vision, 45(2), 83-105.

Yu T., Wu Y., 2006. “Differential Tracking based on

Spatial-Appearance Model (SAM)”, Proceedings of

the IEEE CVPR2006, Vol.1(17-22), pp.720-727, New

York City, NY.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

540