
EVALUATION AND IMPROVEMENTS OF THE LEVEL SET
METHOD FOR RM IMAGES SEGMENTATION
Donatello Conte, Pasquale Foggia, Francesco Tufano and Mario Vento
Dipartimento di Ingegneria dell’Informazione e Ingegneria Elettrica
Universit
`
a degli Studi di Salerno, Via Ponte Don Melillo, 1 - 84084 Fisciano(SA), Italy
Keywords:
Medical Image, Level Set, Image Segmentation.
Abstract:
We present a novel algorithm for the segmentation of bony tissues in MR images. Our approach is based on the
level set algorithm. We introduce some pre-processing phases that improve image quality and segmentation
performance. The technique requires no training and operates semi-automatically, requiring only the entry of
a single seed point within the tissue to be segmented. The proposed approach is more robust than the other
approaches present in the literature, with respect to the position of the initial seed point. The quantitative
analysis of the results on a significant number of images demonstrate the effectiveness of our approach.
1 INTRODUCTION
Despite much effort and significant progress in re-
cent years, image segmentation remains a notoriously
challenging computer vision problem. In particular,
segmentation of medical images is difficult because of
several factors: the complexity of the images; the lack
of anatomical models that fully capture all possible
shape variations for each structure; poor image con-
trast, noise, and missing or diffuse boundaries. Fur-
thermore segmentation of medical images is typically
a semi-automatic process: human interaction intro-
duces an instability in the results because the solu-
tion of most approaches depends considerably on the
choices made by the user at the start of the process.
One of the most widely used methods for image and
shape segmentation in medical images (as we will
show in the next section) is based on curve or bound-
ary evolution. Even though this approach presents ef-
fective solutions in terms of quality of the segmenta-
tion, it has some drawbacks that complicate its prac-
tical employment.
In this paper we present a new algorithm based on the
level set approach that overcomes some of the well
known problems of this kind of algorithms. In partic-
ular the proposed algorithm produces a solution that
is more robust with respect to human interaction: the
results of our algorithm are largely independent of the
initial seed points.
The paper is organized as follows: in section 2 a re-
view of the most used approaches for segmenting MR
images is shown; the proposed algorithm is presented
in section 3 while in section 4 the experimental phase
together with the analysis of the results are described.
Section 5 summarizes the conclusions obtained from
our work.
2 RELATED WORKS
In medical imaging classical segmentation methods,
like Thresholding or Region Growing, have been
substituted with more effective approaches. A well
known approach is to use some classifiers (k-nearest-
neighbor (Vrooman et al., 2007), Bayes classifiers
(Banga et al., 1992)) to segment an image. The pro-
cess of segmentation with classifiers is computation-
ally less expensive than the other approaches. How-
ever there are some drawbacks in the use of this ap-
proach: the first is that it is difficult to take into
account spatial information in the features used for
the classification; the second drawback is that this
approach requires a supervised training phase. For
this reason, some clustering algorithms (unsupervised
classifiers) have been proposed for segmenting the
images: the three most used algorithms are K-means
((Vemuri et al., 1995)), fuzzy c-means ((Ardizzone
et al., 2007), (Foggia et al., 2006)) and expectation-
maximization ((Clark et al., 1994)). One of the main
disadvantage of standard clustering algorithms is that
they depend solely on the intensities of the image
210
Conte D., Foggia P., Tufano F. and Vento M. (2009).
EVALUATION AND IMPROVEMENTS OF THE LEVEL SET METHOD FOR RM IMAGES SEGMENTATION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 210-215
DOI: 10.5220/0001804102100215
Copyright
c
SciTePress

and do not consider spatial context. Furthermore,
these algorithms assume that the intensities of each
class are stationary. This assumption is often incor-
rect in many images due to the intrinsic heterogeneity
of a class, nonuniform illumination, or other imag-
ing artifacts. To take into account spatial information,
Markov Random Field (MRF) Models are often incor-
porated in this kind of algorithms (see (Pappas, 1992),
(Krause et al., 1997)). MRF are very suitable for med-
ical images analysis because in most cases the pixels
belong to the same class of adjacent pixels; in fact,
rarely, anatomical parts are composed by one pixel.
Two critical points of MRF approach are the compu-
tational burden (due to the required iterative optimiza-
tion schemes) and the sensitivity of the results to the
model parameters.
The most used approach in segmentation of medi-
cal images is the level set method ((Cremers et al.,
2005)). Level set is an optimization based method.
A segmentation of the image plane Ω is computed
by locally minimizing an appropriate energy func-
tional E(C) by evolving the contour C of the region
to be segmented starting from an initial contour. In
general, method based on this approach may use ei-
ther an explicit (parametric) or implicit representa-
tion of the contours. In explicit representations ((Leit-
ner and Cinquin, 1991), (McInerney and Terzopoulos,
1995)) – such as splines or polygons – a contour is
defined as a mapping from an interval to the image
domain: C : [0, 1] → Ω. In implicit contour represen-
tations ((Dervieux and Thomasset, 1979), (Osher and
Sethian, 1988)), contours are represented as the (zero)
level line of some embedding function φ : Ω → ℜ:
C = {x ∈ Ω|φ(x) = 0}.
In the original level set algorithm, only gradient infor-
mation is taken into account in the energy term E(C).
Some authors ((Osher and Santosa, 2001), (Chan and
Vese, 2001), (Russon and Paragios, 2002)) have pro-
posed improvements of the classical algorithm by in-
troducing some priors information (e.g. shape, color
or motion information).
Level set algorithms are widely used in medical im-
ages segmentation because they are very effective.
However they present some drawbacks:
• The segmentations obtained by a local optimiza-
tion method are strongly dependent to the initial-
ization. For many realistic images, the segmenta-
tion algorithm tends to get stuck in undesired local
minima (especially in the presence of noise) forc-
ing the user to try with several seed points before
obtaining a satisfactory solution.
• This approach lacks a meaningful probabilistic in-
terpretation. Extensions to other segmentation cri-
teria such as color, texture or motion are not
straight-forward.
• This algorithm has a problem in finding correct
contours of the regions when the region bound-
aries have corners or other singularities.
In this paper we present a novel algorithm based on
level set that overcomes the first of the considered
problems.
3 THE PROPOSED METHOD
To reduce the limits of level set standard algorithm
we propose the follow improvements for the segmen-
tation:
• an image smoothing filter is used to reduce the
noise;
• an image pre-segmentation is performed to make
the results independent of the chosen seed points;
• the final segmentation is based on the Laplacian
level set, to enhance the contour of the tissue of
interest.
In the following subsections, each of these steps is
discussed in more detail.
3.1 Smoothing Filter
One of the main problems in MR image processing
is the noise. To reduce this problem a 3D Gaussian
filter, with a 3x3x3 kernel, is applied to the image be-
fore the segmentation step. The coefficients of the
convolution mask are obtained according to the clas-
sical Gaussian distribution function. The size of the
mask and σ have been empirically chosen. The lat-
ter value has been chosen by performing the mean of
the variances among all the 3x3x3 sub images within
a bone region of a set of training images. After this
phase the resulting image is:
I
f
(x, y, z) =
1
λ
[I(x, y, z) ∗G
σ
(x, y, z)] =
=
1
λ
1
∑
i=−1
1
∑
j=−1
1
∑
k=−1
I(x, y, z)G
σ
(i, j, k)
where λ =
∑
1
i=−1
∑
1
j=−1
∑
1
k=−1
G
σ
(i, j, k).
The smoothing filter has two positive effects: it re-
duces the image noise and the corners are less evident.
3.2 Image Pre-segmentation
The base level set algorithm strongly depends on the
choice of the seed point. The reasons of this prob-
lem depend from the minimization of the energy func-
tional; in fact it is possible to stop the process in a
EVALUATION AND IMPROVEMENTS OF THE LEVEL SET METHOD FOR RM IMAGES SEGMENTATION
211

a)
b)
Figure 1: The effect of the seed point on the segmentation:
a) Energy function diagram showing the energy of the seed
point A and of the found (local) minimum B (the diagram is
a 2D projection of the actual 3D diagram); b) Segmentation
result.
local minimum distant from a global minimum. The
process start from a initial condition; in our applica-
tion the segmentation with the base level set algorithm
can evolve to very different solutions from different,
but very close, seed points.
In figure 1 the point A indicates the initial condition of
the energy function when we choose the seed in figure
1b , while the point B indicate the result of the min-
imization of the energy function. The point A and B
in figure 2a have the same meaning for seed in figure
2b. We can note that choosing two close seed points
we have two very different results of the segmentation
process.
To reduce this dependence we introduce a pre-
segmentation phase using a fast but not much effec-
tive algorithm which does not depend on the energy
function. In this way we will use a larger region in-
stead a single point for the initial condition. The cre-
ated seed region produces an initial value of the en-
ergy function that is close to the global minimum in-
dependently from the point chosen by the user (see
figure 3).
We tried two different algorithms for this phase: re-
gion growing (Adams and Bischof, 1994) and fast
marching (Zhang et al., 2007). The results of both
a)
b)
Figure 2: The segmentation obtained on the same image
of fig. 1, starting from a different seed: a) Energy function
diagram showing the energy of the seed point A and of the
found (local) minimum B (the diagram is a 2D projection
of the actual 3D diagram); b) Segmentation result.
algorithms are similar, so we have chosen the first be-
cause of its minor computational cost. Moreover it
has a small number of parameters with respect of fast
marching algorithm.
In this phase, in order to avoid merging between re-
gions of different tissues, the pre-segmentation algo-
rithm parameters must be tuned so as to prefer over-
segmentation to under-segmentation.
3.3 Laplacian Level Set
The smoothing filter reduces the corner problems, but
at the same time it reduces the contrast of the im-
age causing the loss of information for the contour of
the tissue of interest. This effect generates the classic
under-segmentation problem.
To avoid the under-segmentation problems a deriva-
tive filter is applied at the image to evidence the con-
tours of the bone. The used filter is the Laplacian so
defined:
∇
2
f (x, y, z) =
δ
2
f (x, y, z)
δx
2
+
δ
2
f (x, y, z)
δy
2
+
δ
2
f (x, y, z)
δz
2
The filtered image enhances the contours (see Fig. 4)
and becomes the input image of the level set algo-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
212

a)
b)
Figure 3: Minimum with pre-segmentation: a) Energy func-
tion diagram b) Segmentation result.
Figure 4: Output image of the Laplacian operator.
rithm. After the application of the filter, the energy
term E(C) to minimize (see Section 2) becomes the
follow:
E(C) =
Z
C
inside
(u(x, y, z) −µ
inside
)
2
dxdydz +
+
Z
C
outside
(u(x, y, z) −µ
outside
)
2
dxdydz
where u(x, y, z) is the intensity of the filtered image.
4 EXPERIMENTAL RESULTS
To evaluate the results of the proposed algorithm we
used the precision and recall index so defined:
precision =
T P
T P + FP
recall =
T P
T P + FN
where TP is the number of correctly detected objects
of interest, FP is the number of wrongly detected ob-
jects of interest and FN is the number of missed ob-
jects of interest. These indexes are directly usable
for applications where the objects of interest are ei-
ther completely detected or completely missed. In
our application, instead, the objects of interest are not
atomic regions, so we need to consider also partial
recognition of the tissue of interest. For this reason
TP, FP and FN are so defined:
T P =
|
g ∩ d
|
|
g ∪ d
|
FP =
|
d
|
−
|
d ∩ g
|
|
d
|
FN =
|
g
|
−
|
d ∩ g
|
|
g
|
where g is the set of voxels actually belonging to the
region of interest (ground truth), d is the set of vox-
els detected by the algorithm and
|
·
|
denotes the car-
dinality of a set. It is simple to show that when the
object of interest is perfectly detected precision = 1
and recall = 1; instead when the detection is totally
incorrect precision = 0, and recall = 0.
The algorithm has been tested on 11 MRI of wrists
acquired at low field for a total of 762 bi-dimensional
slices. The ground truth has been manually traced by
medical experts.
We compare the proposed algorithm (LLS) with basic
level set algorithm (BLS) and with basic level set with
pre-segmentation module (PLS). We also compare
our algorithm with another algorithm: Geodesic Ac-
tive Contours (see (Caselles et al., 1997) and (Yan and
Kassim, 2006)). Geodesic Active Contours (GAC)
based algorithms are similar to Level Set based al-
gorithms, but the first are motivated by a curve evolu-
tion approach and not by an energy minimization one.
Comparison between GAC and our algorithm is more
suitable than comparison with only Level Set based
algorithms because GAC are less sensitive to initial
parameters. Also for GAC algorithm we present both
basic algorithm and algorithm with pre-segmentation
module (PGAC).
In the following table we report the results:
EVALUATION AND IMPROVEMENTS OF THE LEVEL SET METHOD FOR RM IMAGES SEGMENTATION
213
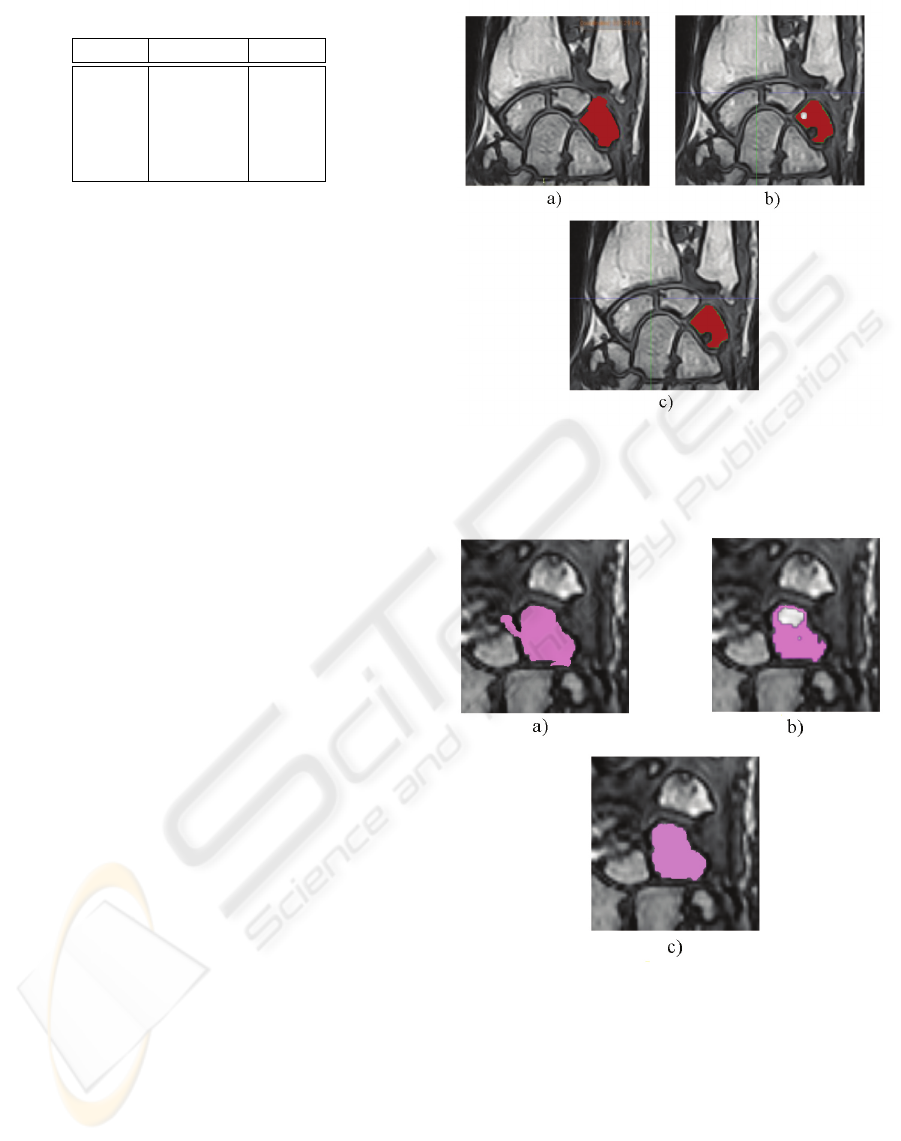
Table 1: Experimental Results.
Precision Recall
BLS 0.81 0.89
PLS 0.92 0.94
GAC 0.95 0.89
PGAC 0.99 0.90
LLS 0.99 0.94
For the algorithm BLS we have manually searched
the best seed point and we have often changed the
calibration parameters. The results shown in table 1
are performed considering the best segmentation ob-
tained for any image. It is important to note that we
are not sure that the chosen seed is really optimal in
the mathematical sense.
Even if the algorithm could in theory produce better
results, in practical use it is not possible to proceed
in this way because of the high effort in the calibra-
tion phase and because of an uncertainty factor on the
results. So we apply the pre-segmentation step also
to the BLS algorithm, to compare this latter with our
proposal independently of the chosen seed.
In conclusion it is important to remark that the idea
of the pre-segmentation phase is necessary for the re-
sult repeatability. Furthermore the Laplacian operator
improve the precision of the results (see table 1).
Under-segmentation problem is present in an algo-
rithm with a low value of precision. This is the case
of BLS: the basic algorithm is not able to recognize
blurred contours (often presents in RM images). With
our pre-segmentation module all algorithms improve
their results with respect of the precision index.
The algorithms with a low value of recall present
over-segmentation problems. Table 1 shows that
BLS, GAC and PGAC are over-segmenting.
We can conclude that Geodesic Active Contours
based approaches are very effective to find tissues
contours, but they often present missing voxels within
the tissue: these approaches are very sensitive to
brightness variability. Level Set based approaches are
not able to find blurred contours: in these approaches
local information give weak contribution to the final
solution.
In any case, Table 1 shows that our approach is more
effective than all others. To have a visual idea of the
effectiveness of our proposed algorithm, in Fig. 5a
and Fig. 6a, Fig. 5b and 6b, Fig. 5c and Fig. 6c
results of the application of Basic Level Set with pre-
segmentation phase, Geodesic Active Contours with
pre-segmentation phase and Laplacian Level Set are
respectively shown. Note that the images result of
the PLS algorithm, obtained after a difficult calibra-
tion phase, is not able to avoid the under-segmentation
Figure 5: a) Basic Level Set with pre-segmentation; b)
Geodesic Active Contours with pre-segmentation; c) Lapla-
cian Level Set.
Figure 6: a) Basic Level Set with pre-segmentation; b)
Geodesic Active Contours with pre-segmentation; c) Lapla-
cian Level Set.
problem and the images result of PGAC algorithm
presents some holes within the tissue.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
214

5 CONCLUSIONS
A new algorithm for segmenting MR images is pro-
posed. The algorithm is based on the level set ap-
proach and is conceived to overcome some of the dif-
ficulties of the original level set method: the solution
is repeatable as regard as changes in initial conditions
and the precision of the result is very high. This algo-
rithm can be used for many applications in the field of
Computer Aided Diagnosis.
Currently we are working on the extension of the ex-
periments to assess the results. Then we will analyse
the new results to find other improvements to the de-
scribed method.
REFERENCES
Adams, R. and Bischof, L. (1994). Seeded region growing.
IEEE Transaction on Pattern Analysis and Machine
Learning, 16(6):641–647.
Ardizzone, E., Pirrone, R., and Gambino, O. (2007). Fuzzy
C-Means Segmentation on Brain MR Slices Corrupted
by RF-Inhomogeneity, chapter 48, pages 378–384.
Springer-Verlag.
Banga, C., Ghorbel, F., and Pieczynski, W. (1992). Un-
supervised bayesian classifier applied to the segmen-
tation of retina image. IEEE Proceedings of the An-
nual International Conference of the Engineering in
Medicine and Biology Society, 5:1847–1848.
Caselles, V., Kimmel, R., and Sapiro, G. (1997). Geodesic
active contours. International Journal of Computer
Vision, 22-1:61–79.
Chan, T. and Vese, L. (2001). Active contours without edge.
IEEE Transaction on Image Processing, 10(2):266–
277.
Clark, M. C., Hall, L. O., Goldgof, D., Clarke, L. P.,
Velthuizen, R., and Silbiger, M. S. (1994). Mri seg-
mentation using fuzzy clustering techniques. IEEE
Engineering in Medicine and Biology, 13(5):730–742.
Cremers, D., Rousson, M., and Deriche, R. (2005). Review
of statistical approaches to level set segmentation: In-
tegrating color, texture, motion and shape. Interna-
tional Journal on Computer Vision, 19(10):1–35.
Dervieux, A. and Thomasset, F. (1979). A finite element
method for the simulation of raleigh-taylor instability.
Springer Lecture Notes in Mathematics, 771:145–158.
Foggia, P., Guerriero, M., Percannella, G., Sansone, C.,
Tufano, F., and Vento., M. (2006). A graph-based
method for detecting and classifying clusters in mam-
mographic images. In et al, D.-Y. Y., editor, Lecture
Notes in Computer Science, volume 4109, pages 484–
493. Springer-Verlag, Berlin.
Krause, B., Wells, W., Kikinis, R., Held, K., and Kops, E.
(1997). Markov random field segmentation of brain
mr images. IEEE Transaction on Medical Imaging,
16(6):878–886.
Leitner, F. and Cinquin, P. (1991). Complex topology 3d ob-
jects segmentation. In SPIE Conference on Advances
in Intelligent Robotics Systems.
McInerney, T. and Terzopoulos, D. (1995). Topologically
adaptable snakes. In 5th International Conference on
Computer Vision, pages 840–845. IEEE Comp. Soc.
Press.
Osher, S. and Santosa, F. (2001). Level set medhods for
optimization problems involving geomertry and con-
straints i. frequencies of a two-density inhomogeneous
drum. Journal of Computational Physics, 171:272–
288.
Osher, S. J. and Sethian, J. A. (1988). Fronts propagation
with curvature dependent speed: Algorithms based
on hamiltonjacobi formulations. Journal of Compu-
tational Physics, 79:12–49.
Pappas, T. (1992). An adaptive clustering algorithm for im-
age segmentation. IEEE Transaction on Signal Pro-
cessing, 40.
Russon, M. and Paragios, N. (2002). Shape priors for level
set representation. Lecture Notes in Computer Sci-
ence, 2351:78–92.
Vemuri, B. C., Rahman, S. M., and Li, J. (1995). Multires-
olution adaptive k-means algorithm for segmentation
of brain mri. In ICSC ’95: Proceedings of the Third
International Computer Science Conference on Image
Analysis Applications and Computer Graphics, pages
347–354. Springer-Verlag.
Vrooman, H. A., Cocosco, C. A., van der Lijn, F., Stokking,
R., Ikram, M. A., Vernooij, M. W., Breteler, M. M.,
and Niessen, W. J. (2007). Multi-spectral brain tissue
segmentation using automatically trained k-nearest-
neighbor classification. NeuroImage, 37(1):71–81.
Yan, P. and Kassim, A. A. (2006). Segmentation of volu-
metric mra images by using capillary active contour.
Medical Image Analysis, 10:317–329.
Zhang, H., Zhang, J., Cao, J., Wang, W., Gong, J., and
Wang, X. (2007). Robust fast marching method based
on anisotropic diffusion. In Third International Con-
ference on Natural Computation, volume 3, pages
159–162.
EVALUATION AND IMPROVEMENTS OF THE LEVEL SET METHOD FOR RM IMAGES SEGMENTATION
215
