A PETRI NET MODEL OF PROCESS PLATFORM-BASED

PRODUCTION CONFIGURATION

Linda L. Zhang and Brian Rodrigues

Department of Operations, University of Groningen, Landleven 5, Groningen, The Netherlands

Lee Kong Chian School of Business, Singapore Management University, Singapore

Keywords: Process platform, Production configuration, Hierarchical Petri nets, Colored Petri nets, Timed Petri nets.

Abstract: In the literature process platform-based production configuration (PPbPC) has been proposed to obtain

efficiency in product family production. In this paper, we present a holistic view of PPbPC, attempting to

facilitate understanding and implementation. This is accomplished through dynamic modelling and

graphical representation based on Petri nets (PNs) techniques. To cope with the modelling difficulties, we

develop a new formalism of hierarchical colored timed PNs (HCTPNs) by integrating the basic principles of

hierarchical PNs, timed PNs and colored PNs. In the formalism, three types of nets together with a system

of HCTPNs are defined to address the fundamental issues in PPbPC. A case study of electronics products is

also reported to demonstrate PPbPC using the proposed formalism.

1 INTRODUCTION

While designing families of related products based

on product platforms has been recognized as an

effective means of quickly fulfilling diverse

individualized customer requirements at low costs,

to efficiently produce these products, methods to

plan production processes by considering the

optimality of the cohort of an entire family rather

than individual products must be developed, as

pointed out by, e.g., EIMaraghy (2006), WiendahI et

al. (2007). The reported studies (e.g., Bley and

Zenner, 2006; EIMaraghy, 2007; Schierholt, 2001;

Williams et al., 2007) introduce concepts such as

process parameter platform, process configuration,

reconfigurable process planning, variant-oriented

planning to plan either manufacturing or assembly

processes for part or assembly families, which are

the components of end-product families. On the

other hand, efficient production of component parts

or assemblies alone is not enough to ensure effective

advantages for a company since end-products,

instead of parts or assemblies, are the focus (Silva

and Alves, 2006).

In response to the limitations of the existing

research, Zhang (2007) proposes process platform-

based production configuration (PPbPC) to help

companies plan production processes for end-

product families where both component parts and

assemblies are considered. The published work has

separately addressed issues pertaining to PPbPC

from different aspects, e.g., the structural model of a

process platform (Zhang et al., 2007), the mapping

relationships between product and process variety

inherent in PPbPC (Jiao et al., 2007), to name but

two, without presenting a complete picture. This

study, thus, attempts to introduce a holistic view of

PPbPC to facilitate understanding and

implementation. It is accomplished by developing a

dynamic model of PPbPC, i.e., modelling how

production processes are configured from a process

platform for a given product family.

Among the modelling techniques such as data

flow graphs, UML, Petri nets (PNs) and workflow

management coalition formalism, the comparison

results of some studies have proven that PNs are the

most desirable one to model complex

systems/processes due to their graphical

representation, formal analysis and executability

(Cortes et al., 2003; Dussart et al., 2004). Thus, in

this study we adopt PN techniques. The fundamental

issues in PPbPC discussed in (Zhang, 2007) result in

several modelling challenges, including handling

product and process variety, accommodating process

variations, dealing with configuration granularities

and satisfying constraints. To meet these unique

modelling difficulties, in this study we develop a

new formalism of hierarchical colored PNs

(HCTPNs) based on the principles of colored PNs

(Jensen, 1997), timed PNs (Ramachandani, 1974)

5

L. Zhang L. and Rodrigues B. (2009).

A PETRI NET MODEL OF PROCESS PLATFORM-BASED PRODUCTION CONFIGURATION.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Information Systems Analysis and Speciﬁcation, pages 5-12

DOI: 10.5220/0001804400050012

Copyright

c

 SciTePress

and hierarchical PNs (Fehling, 1993). In the

following two sections, an overview of PPbPC and

an industrial example which we use to demonstrate

the modelling of PPbPC based on the proposed

formalism are introduced, respectively.

2 OVERVIEW OF PPBPC

2.1 Process Platform

In relation to a product family, a process family

refers to a set of production processes which fulfil

all individual products belonging to the family

(Zhang, 2007). As with the common product

structure assumed by all products in a family, a

common process structure is inherent in the

corresponding process family. In essence, a process

platform entails a conceptual structure and overall

logical organization of a process family in relation to

a product family. It provides a generic umbrella to

capture and utilize commonality in planning

production processes for the product family. More

specifically, a process platform is underpinned by an

integrated product-process structure common to both

the product and process families. Thus, a process

platform includes all design data pertaining to the

product family, e.g., assemblies, parts, design

parameters, value instances, and these of the process

family, e.g., operations, manufacturing resources

(i.e., machines, tools, fixtures, jigs, etc), setups.

These product and process family data are organized

by following the material requirement links (i.e., the

links among material inputs, operations and product

outputs) in general, the mapping relationships

enabled by design parameters and their value

instances in particular (Zhang et al., 2007).

2.2 Production Configuration

Within a process platform, for a given member of

the associated product family, production

configuration takes the BOM (i.e., bill of materials)

and a list of product specifications of a given

product as inputs. The proper process elements, such

as abstract processes for individual product items

(including the end-product), operations, machines,

tools, fixtures, estimated cycle times, and setups are

then selected. Subsequently, these selected process

elements are arranged into feasible production

processes, where the abstract processes are replaced

with process details, for producing the given end-

product. Both selection and arrangement are subject

to constraints among product and process data.

Finally, evaluation of the configured multiple

feasible production processes takes place to

determine the most appropriate one.

In line with the fact that the hierarchical

structure of a product can be regarded as a collection

of independent product items organized at different

levels of abstraction, production configuration is an

iterative process of configuring process for each

product item specified in the BOM along the

hierarchical structure per se. At each configuration,

only the child items at the immediate lower level are

considered. It starts with the end-product at the top

level of the hierarchy. The results are: 1) abstract

processes for the immediate child items - be they

parts or assemblies, 2) assembly operations

involving these child items and WIPs (work in

processes), 3) manufacturing resources required to

complete the corresponding operations, estimated

cycle times and setups, and 4) precedence

relationships between operations. Fig. 1 shows

production configuration for an item: PI, which has

five immediate child items: A, B, C, D and E.

According to the input specifications, five abstract

processes for the five child items are selected first;

the assembly operations along with manufacturing

resources joining the child items are specified and

ordered into a sequence.

PI

A

B

C

D

E

O4

O3

O2

O1

: Product item; : Assembly operation;

: Abstract process

: Produce; : Operations precedence; : Material input

P

E

P

D

P

A

P

B

P

C

: Parent-child releationship

PI

A

B

C

D

E

O4

O3

O2

O1

: Product item; : Assembly operation;

: Abstract process

: Produce; : Operations precedence; : Material input

P

E

P

D

P

A

P

B

P

C

: Parent-child releationship

Figure 1: Configuring process elements in production

configuration.

After the configuration process for an end-

product, configuration continues to the child items at

the immediate lower level. Each child item, in turn,

is treated as an end-product, and its abstract process

specified previously is refined accordingly. The

complete production process for the product is

formed by replacing the abstract processes at higher

levels with the refined processes at lower levels.

Thus, complete production processes consider all

processes for child items listed in products’ BOMs

and cover all operations starting from these

involving raw materials.

ICEIS 2009 - International Conference on Enterprise Information Systems

6

3 AN INDUSTRIAL EXAMPLE

The industrial example adopted is the manufacturing

of vibration motors for mobile phones produced by

an electronics company. The increasing variations in

mobile phone design lead to large numbers of

customized vibration motors to be produced.

Together with other factors (e.g., short delivery lead

times), the high variety of vibration motors

complicate the planning of their production

processes. In line with the common product structure

underlying this vibration motor family, the process

platform has been constructed a priori. Fig. 2 shows

the integrated generic product-process structure

underpinning the process platform.

In the figure, each node represents a family of

items (or processes) of a same type. For example,

AP_VM is the family of assembly processes

producing the vibration motor family (VM). It takes

variants from 3 assembly families: FA (frameassy),

AA (armtureassy) and BA (bracketassy) and variants

from 2 part families: Wt (weight) and Rh (rubber

holder) as material inputs. While the 3 assembly

families are common to all motors in the family, the

2 part families are optional in the sense that not all

of motor variants assume Wt and/or Rh variants.

Another 4 assembly process families, including

AP_BA, AP_AA, AP_FA and AP_CA, produce

assembly families BA, AA, FA and CA (coilassy),

respectively. Further, 3 part families: Ba (bracket a),

Bb (bracket b) and Tl (terminal), are the material

inputs of AP_BA; CA and a part family: St (shaft)

the material inputs of AP_AA; 2 part families: Fm

(frame) and Mt (magnet) the material inputs of

AP_FA; and 3 part families: Ct (commutator), Tp

(tape) and Cl (coil) the material inputs of AP_CA.

Among the part families, the company manufactures

Ba, Bb, Ct and Cl and outsources others. Moreover,

the company has alternative machines for producing

same product items. In most cases, these operations

take different cycle times.

4 NET DEFINITIONS

In the formalism, a number of net elements are

defined first. To capture and model product and

process variety while building a concise and

representative model of PPbPC, colors (i.e., specific

data values pertaining to various objects) are

attached to tokens, resulting colored tokens.

According to the places that they reside in, colored

tokens model different product and process

elements.

CA

St

Mt

Fm

Cl

Ct

Ba

Bb

Tl

: A generic part;

: A generic assembly;

AP_VM

AP_FA

AP_AA

AP_BA

AP_CA

MP_Ba

MP_Bb

Tp

VM

Rh

BA

AA

FA

Wt

MP_Ct

RM

Ct

RM

Ba

RM

Bb

MP_Cl

RM

Cl

: A generic process

: Material input

: Product output

: A generic material

CA

St

Mt

Fm

Cl

Ct

Ba

Bb

Tl

: A generic part;

: A generic assembly;

AP_VM

AP_FA

AP_AA

AP_BA

AP_CA

MP_Ba

MP_Bb

Tp

VM

Rh

BA

AA

FA

Wt

MP_Ct

RM

Ct

RM

Ba

RM

Bb

MP_Cl

RM

Cl

: A generic process

: Material input

: Product output

: A generic material

Figure 2: The process platform of the motor family.

In accordance with practice, buffer places (

B

P

)

are introduced to represent buffers. In general, any

item, be it a part, assembly, or WIP, has 3 statuses:

staying in a buffer, ready to be processed and being

processed. Thus, item places (

I

P

) are defined to

represent items that are ready to be processed and

being processed. Machine places (

R

P

) are defined to

represent machines (including the corresponding

tools, fixtures, setups, etc.) that are available for

operations. While tokens in

R

P

indicate idle

machines, tokens in items-being-processed places

imply that machines are busy. Conceptual machine

places (

CR

P

) are defined to represent the conceptual

machines of the set of alternatives that can work on

same items to complete same tasks. When there is a

colored token available in a conceptual machine

place, the conceptual machine is instantiated to the

specific machine represented by the colored token.

Reconfigurable transitions (

R

T

) are defined to

accommodate the modeling of adopting one machine

among the available alternatives for given items.

Inhibitor arcs (

h

) are defined to connect

CR

P

to

R

T

and take two values, 0 and 1.

(

)

RCR

Tt,Pp,1t,ph ∈∈∀=

indicates there is a token

in the conceptual machine place, and the associated

reconfigurable transition is disabled and cannot fire.

When

(

)

,0,

=

tph

no tokens reside in the conceptual

machine place; and the associated reconfigurable

transition can fire if it is enabled.

Essentially,

h

,

R

T

and

CR

P

form a

reconfiguration mechanism to model the situations,

where multiple machines can perform same tasks

and only one is used eventually. The firing of

R

T

leads to the reconfiguration of appropriate machines.

In this way,

CR

P

,

R

T

and

h

work together to

address process variations in system models without

A PETRI NET MODEL OF PROCESS PLATFORM-BASED PRODUCTION CONFIGURATION

7

rebuilding new ones when machines are added

and/or removed.

Logical transitions (

L

T

) are defined to capture

the logic of system running. Their firing indicates

the satisfaction of preconditions of operations

execution. Timed transitions (

T

) represents

operations, which take certain time durations to

complete. Accordingly, the firing of timed

transitions incurs time delays indicating operations

cycle times. Both the logical and reconfigurable

transitions are untimed. Their firing is atomic and

takes 0 time delay. To cope with difficulties in

modeling diverse cycle times associated with

multiple machines and same/different material

items, timed arc expressions, to which time delays

are attached, are introduced in the proposed

formalism. The time delays in timed arc expressions

are, in fact, equal to the firing time durations of the

relevant timed transitions. Refinement transitions

(

r

T

) are introduced as an abstraction mechanism,

representing abstract processes of component parts

/assemblies, which will be elaborated in next steps.

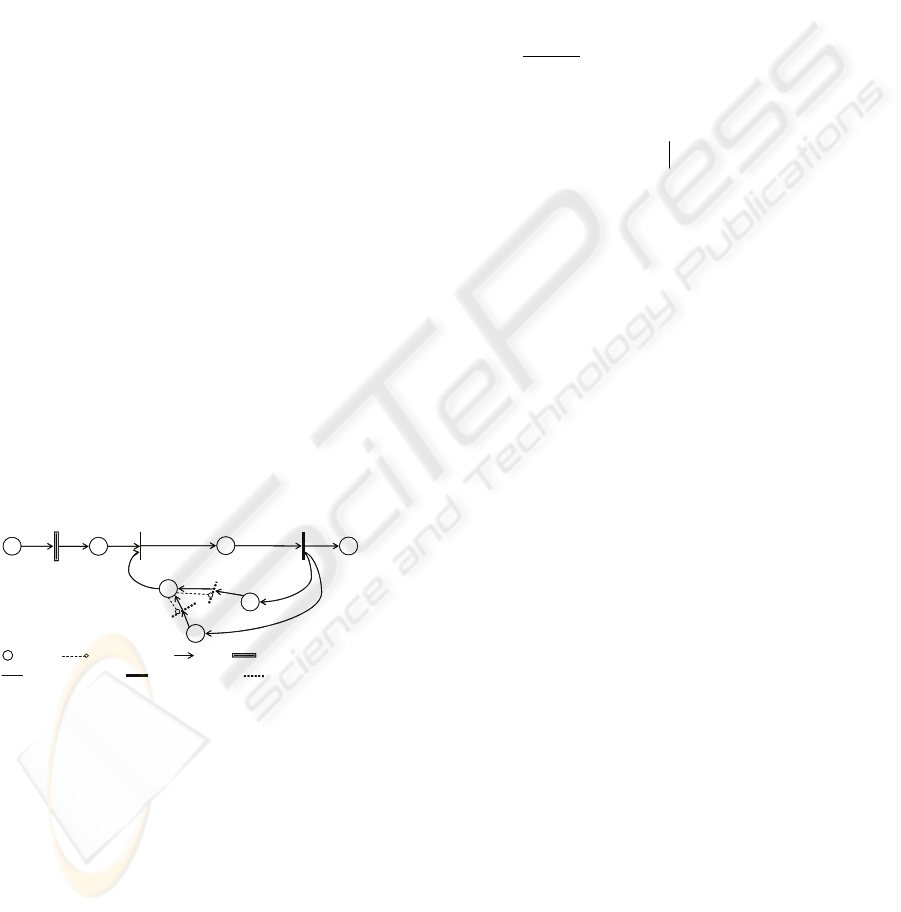
Fig. 3 shows the graphical formalism of the

above net elements and a simple PN constructed

using these elements. Tokens are not shown in the

PN model.

3546271

p/p,p/p,p/p,p are

buffer/item/machine/ conceptual machine places,

respectively. Based on these net elements, three

types of PNs, namely manufacturing nets (

MNets

),

assembly nets (

ANets ) and process nets (

PNets

) are

defined to address PPbPC modeling with respect to

different levels of abstraction.

: Place;

: Logical transition;

: Arc;

: Reconfigurable transition

: Inhibitor arcs;

: Timed transition;

2

p

7

p

2

t

5

t

3

t

6

p

4

p

5

p

3

p

4

t

1

p

1

t

: Refinement transition: Place;

: Logical transition;

: Arc;

: Reconfigurable transition

: Inhibitor arcs;

: Timed transition;

2

p

7

p

2

t

5

t

3

t

6

p

4

p

5

p

3

p

4

t

1

p

1

t

: Refinement transition

Figure 3: The graphical formalism and a simple PN model.

4.1 Manufacturing Net (MNet)

A manufacturing net ( MNet ) models the processes

to manufacture a family of component parts:

(

)

μτΕΕαΣ

,,,,,V,,h,A,T,PMNet

T

=

, where

•

CRRIB

P

∪∪∪= is a finite nonempty set

of places with 4 disjoint subsets;

•

φ

=∩∪∪= TP,TTTT

TRL

is a finite nonempty

set of transitions with 3 disjoint subsets;

•

PTTPA ×∪×⊆ is a finite nonempty set of

arcs;

•

φ

=∩×⊆ Ah,TPh

RCR

is a finite nonempty set

of inhibitor arcs;

•

Σ

is a set of types or color sets;

•

Σ

⊆V,V

is a set of variables;

•

Σ

α

6P:

is an assignment function that maps

a place

p to a color set

(

)

p

α

;

•

T

Ε

is an expression function that maps arcs

IL

P

T

×

to timed expressions such that

(

)

(

)

(

)

I

MS

T

pp,tEType ∧=

α

(

)

(

)

(

)

()

ILT

PTp,t,p,tEVarType ×∈∀ℜ∈∧⊆

+

τΣ

where

(

)

MS

p

α

is a multiset over

(

)

p

α

;

•

VAPT

IL

6∩×:

Ε

is an expression function

mapping arcs other than

IL

P

T

×

to untimed

expressions consisting of

Vv

i

∈

such that

(

)

(

)

,pvType

MS

i

α

=

T

Tttp ∈∉∀

•

;

•

0∪ℜ∈

+

τ

is a set of non-negative real numbers

representing time delays;

•

FMS

P

Σ

μ

6: is a marking function specifying

the distribution of colored tokens in all places,

where

FMS

Σ

is the family of all multisets over

Σ

.

An

MNet involves a series of specific operations

fabricating parts from raw materials and, does not

involve refinement transitions. In this study, we

adopt cycle times to accommodate the selection of

machines and processes by considering time-related

production performances. Accordingly, time delays,

τ

, represent operations cycle times.

The timed arc expression function maps each

arc, which connects a logical transition to an items-

being-processed place, to a timed arc expression. It

involves several variables that form an antecedent-

consequent statement. Each variable belongs to a

certain color type, thus assuming a set of values (i.e.,

colored tokens). While the multiple variables in an

antecedent relate to colored tokens modeling

material items and machines, the single variable in a

consequent corresponds to colored tokens of product

items. Accordingly, evaluating a timed arc

expression is accomplished by associating different

combinations of colored tokens of materials items

and machines with variables in the antecedent. The

evaluation yields different colored tokens of product

items in the consequent along with the

corresponding time delays. The untimed arc

expression function specifies expressions for all

arcs, excluding inhibitor arcs and these connecting

logical transitions to items-being-processed places.

Untimed arc expressions contain variables which

have the same color types as the associated places;

and they are evaluated by associating colored tokens

in the corresponding places with their variables. The

ICEIS 2009 - International Conference on Enterprise Information Systems

8

evaluation leads to (1) input tokens for firing the

corresponding transitions; and (2) output tokens

after firing timed and reconfigurable transitions.

Based on the above definition and by following

the common process flows of manufacturing part

variants in the 4 part families in the motor family, 4

MNets

,

Ct_MNet,Bb_MNet,Ba_MNet

and

Cl_MNet

, are

constructed in accordance with

Bb_MP,Ba_MP

and

Cl_MP

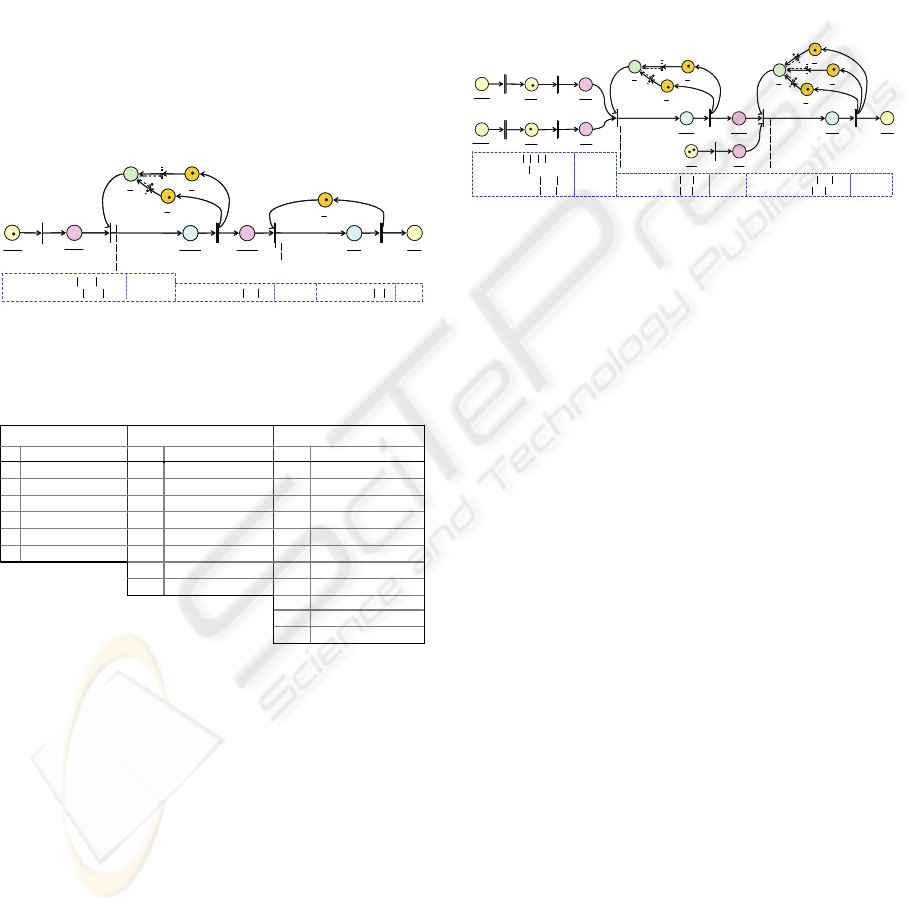
in Fig. 2. Due to space constraints, rather

than all nets, only

Ba_MNet

to manufacture Ba

family is presented, as shown in Fig. 4. For

illustrative simplicity, colored tokens defined in

relation to 3 Ba variants are shown in the figure.

Also shown are color types/colored tokens defined

for each place and variables. Table 1 lists the places

and represented system elements.

321

RBaRBaRBawithFRBacoltype =

FRBaxvar

1

:

1Ba1Bb1Bawith1FBacoltype

321

⋅⋅⋅=⋅

1FBaxvar

2

⋅:

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBa

1FBa ⋅ FBa

R

2

x

r

3

m

8.4@1Bam,RBa

4.4@1Bam,RBa

5.4@1Bam,RBa

7.3@1Bam,RBa

9.5@1Bam,RBa

3.5@1Bam,RBa

ofr,xcase

323

313

222

212

121

111

1

+⋅→

5.1@Bam,1Ba

7.1@Bam,1Ba

1.1@Bam,1Ba

ofr,xcase

333

232

131

3

+→⋅

1

m

2

m

1

m

2

m

1

m

2

m

FRBa

1

x

3

x

321

BaBaBawithFBacoltype =

FBaxvar

3

:

321

mmmwithRcoltype =

Rrvar :

1

x

1

x

2

x

3

x

2

x

1FBa ⋅ FBa

3

m

321

RBaRBaRBawithFRBacoltype =

FRBaxvar

1

:

1Ba1Bb1Bawith1FBacoltype

321

⋅⋅⋅=⋅

1FBaxvar

2

⋅:

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBa

1FBa ⋅ FBa

R

2

x

r

3

m

8.4@1Bam,RBa

4.4@1Bam,RBa

5.4@1Bam,RBa

7.3@1Bam,RBa

9.5@1Bam,RBa

3.5@1Bam,RBa

ofr,xcase

323

313

222

212

121

111

1

+⋅→

5.1@Bam,1Ba

7.1@Bam,1Ba

1.1@Bam,1Ba

ofr,xcase

333

232

131

3

+→⋅

1

m

2

m

1

m

2

m

1

m

2

m

FRBa

1

x

3

x

321

BaBaBawithFBacoltype =

FBaxvar

3

:

321

mmmwithRcoltype =

Rrvar :

1

x

1

x

2

x

3

x

2

x

1FBa ⋅ FBa

3

m

Figure 4: The

Ba_MNet

of the bracket a family.

Table 1: The places, represented elements and colored

tokens.

Ba_MNet

B

A_ANet

P

Ne

t

Places System Elements Places System Elements Places System Elements

1

p

A buffer for raw materials of Ba

4/1

p

Buffers for raw materials of Ba/Bb

7/6/5/2/1

p

Assembly/part buffers for CA/St/Ba/Bb/Tl

7/2

p

Variants of RBa/Ba

•

1 ready to be processed

12/5/2

p

Part buffers for Ba/Bb/Tl

27/25/17/16

p

Part buffers for Fm/Mt/Wt/Rh

3

p

A conceptual machine for manufacturing Ba

13/6/3

p

Variants of Ba/Bb/Tl ready to be processed

18/4/3

p

Assembly buffers for AA/BA/FA

8/6/5

p

Machines for manufacturing Ba

14/7

p

Conceptual machines for assembling Bab/BA

19/9/8

p

Variants of AA/BA/FA ready to be processed

9/4

p

Variants of RBa/Ba

•

1 being manufactured

15/8

p

Variants of Bab/BA being processed

28/26

p

Variants of Wt/Rh ready to be processed

10

p

A buffer for Ba

18/17/16/10/9

p

Alternative machines for assembling Bab/BA

20/10

p

Conceptual machines for assembling AB/MB

11

p

Variants of Bab ready to be processed

23/22/14/13/12

p

Alternative machines for forming AB/MB

19

p

An assembly buffer for BA

29

p

The final assembly workstation

30/21/11

p

Variants of AB/MB/VM being assembled

24/15

p

Variants of AB/MB ready to be processed

31

p

A buffer for vibration motors

4.2 Assembly Net (ANet)

An assembly net (

ANet

) is defined to represent the

processes of forming an assembly family:

(

)

μτΕΕαΣ

,,,,,V,,h,A,T,PANet

T

=

.

While

τΕΕαΣ

,,,,V,,h,A,P

T

and

μ

carry the

same meaning as these in an MNet,

φ

=∩∪∪∪= TP,TTTTT

TRLr

is a finite nonempty

set of transitions with 4 disjoint subsets.

An

ANet

consists of assembly operations

involving the immediate child items of an assembly

family. It also includes the WIPs formed by the

immediate child items. Refinement transitions are

introduced in an

ANet

to represent abstract

manufacturing processes of child parts and abstract

assembly processes of child assemblies, which are to

be elaborated subsequently. While an

ANet

involves

raw material buffers and parts buffers that are

common to

MNets

as well, it has unique assembly

buffers. Similarly, 4

ANets ,

,AA_ANet,BA_ANet

FA_ANet

and

CA_ANet

, are constructed in

accordance with

FA_AP,AA_AP,BA_AP

and

CA_AP

in Fig. 1. Fig. 5 shows

BA_ANet

to produce

B

A

family. The places and represented system elements

are listed in Table 1 as well.

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRBb

11

t

12

t

14

t

7

t

6

t

9

t

FBa

FRBa

FBb

FBab

FTl

FBA

R

1

x

3

x

4

x

r

3

m

4

m

5

m

3

m

4

m

5

m

3

m

4

m

5

m

3.6@Babm,Bb,Ba

3.5@Babm,Bb,Ba

1.6@Babm,Bb,Ba

6.5@Babm,Bb,Ba

9.4@Babm,Bb,Ba

3.4@Babm,Bb,Ba

ofr,y,xcase

3233

3133

2222

2122

1211

1111

22

+→

2.4@BAm,Tl,Bab

0.3@BAm,Tl,Bab

5.3@BAm,Tl,Bab

9.3@BAm,Tl,Bab

8.2@BAm,Tl,Bab

2.3@BAm,Tl,Bab

0@BABab

ofr,z,xcase

3523

3423

3323

2512

2412

2312

11

13

+→

1

m

2

m

1

m

2

m

1

m

2

m

1

z

2

z

FBa

FBb

FBab

FTl

FBA

2

x

2

x

2

x

2

x

1

y

2

y

2

y

2

y

2

y

3

x

4

x

2

z

321

RBaRBaRBawithFRBacoltype =

FRBaxvar

1

:

321

RBbRBbRBbwithFRBbcoltype =

FRBbyvar

1

:

321

BaBaBawithFBacoltype =

FBaxvar

2

:

321

BbBbBbwithFBbcoltype =

FBbyvar

2

:

321

BabBabBabwithFBabcoltype =

FBabxvar

3

:

321

BABABAwithFBAcoltype =

FBAxvar

4

:

21

TlTlwithFTlcoltype =

FTlzvar

1

:

54321

mmmmmwithRcoltype =

Rrvar :

3

x

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRBb

11

t

12

t

14

t

7

t

6

t

9

t

FBa

FRBa

FBb

FBab

FTl

FBA

R

1

x

3

x

4

x

r

3

m

4

m

5

m

3

m

4

m

5

m

3

m

4

m

5

m

3.6@Babm,Bb,Ba

3.5@Babm,Bb,Ba

1.6@Babm,Bb,Ba

6.5@Babm,Bb,Ba

9.4@Babm,Bb,Ba

3.4@Babm,Bb,Ba

ofr,y,xcase

3233

3133

2222

2122

1211

1111

22

+→

2.4@BAm,Tl,Bab

0.3@BAm,Tl,Bab

5.3@BAm,Tl,Bab

9.3@BAm,Tl,Bab

8.2@BAm,Tl,Bab

2.3@BAm,Tl,Bab

0@BABab

ofr,z,xcase

3523

3423

3323

2512

2412

2312

11

13

+→

1

m

2

m

1

m

2

m

1

m

2

m

1

z

2

z

FBa

FBb

FBab

FTl

FBA

2

x

2

x

2

x

2

x

1

y

2

y

2

y

2

y

2

y

3

x

4

x

2

z

321

RBaRBaRBawithFRBacoltype =

FRBaxvar

1

:

321

RBbRBbRBbwithFRBbcoltype =

FRBbyvar

1

:

321

BaBaBawithFBacoltype =

FBaxvar

2

:

321

BbBbBbwithFBbcoltype =

FBbyvar

2

:

321

BabBabBabwithFBabcoltype =

FBabxvar

3

:

321

BABABAwithFBAcoltype =

FBAxvar

4

:

21

TlTlwithFTlcoltype =

FTlzvar

1

:

54321

mmmmmwithRcoltype =

Rrvar :

321

RBaRBaRBawithFRBacoltype =

FRBaxvar

1

:

321

RBbRBbRBbwithFRBbcoltype =

FRBbyvar

1

:

321

BaBaBawithFBacoltype =

FBaxvar

2

:

321

BbBbBbwithFBbcoltype =

FBbyvar

2

:

321

BabBabBabwithFBabcoltype =

FBabxvar

3

:

321

BABABAwithFBAcoltype =

FBAxvar

4

:

21

TlTlwithFTlcoltype =

FTlzvar

1

:

54321

mmmmmwithRcoltype =

Rrvar :

321

RBaRBaRBawithFRBacoltype =

FRBaxvar

1

:

321

RBbRBbRBbwithFRBbcoltype =

FRBbyvar

1

:

321

BaBaBawithFBacoltype =

FBaxvar

2

:

321

BbBbBbwithFBbcoltype =

FBbyvar

2

:

321

BabBabBabwithFBabcoltype =

FBabxvar

3

:

321

BABABAwithFBAcoltype =

FBAxvar

4

:

21

TlTlwithFTlcoltype =

FTlzvar

1

:

54321

mmmmmwithRcoltype =

Rrvar :

3

x

Figure 5: The BA_ANet of the bracketassy family.

4.3 Process Net (PNet)

A process net (

PNet

) is defined to represent the

processes of producing an end-product

family:

(

)

μτΕΕαΣ

,,,,,V,,h,A,T,PPNet

T

=

, where

the components are as for an

ANet

.

A

PNet

, de facto, is a special

ANet

in that end-

products themselves are assemblies. Thus, it

includes the assembly operations associated with

immediate child items. Also included are the WIPs

formed by these child parts and assemblies. In

addition to buffers for raw materials, parts and

assemblies, buffers for end-products are defined in a

PNet

. In line with the manufacturing and assembly

processes of immediate child items, a number of

refinement transitions are introduced in a

PNet

. In a

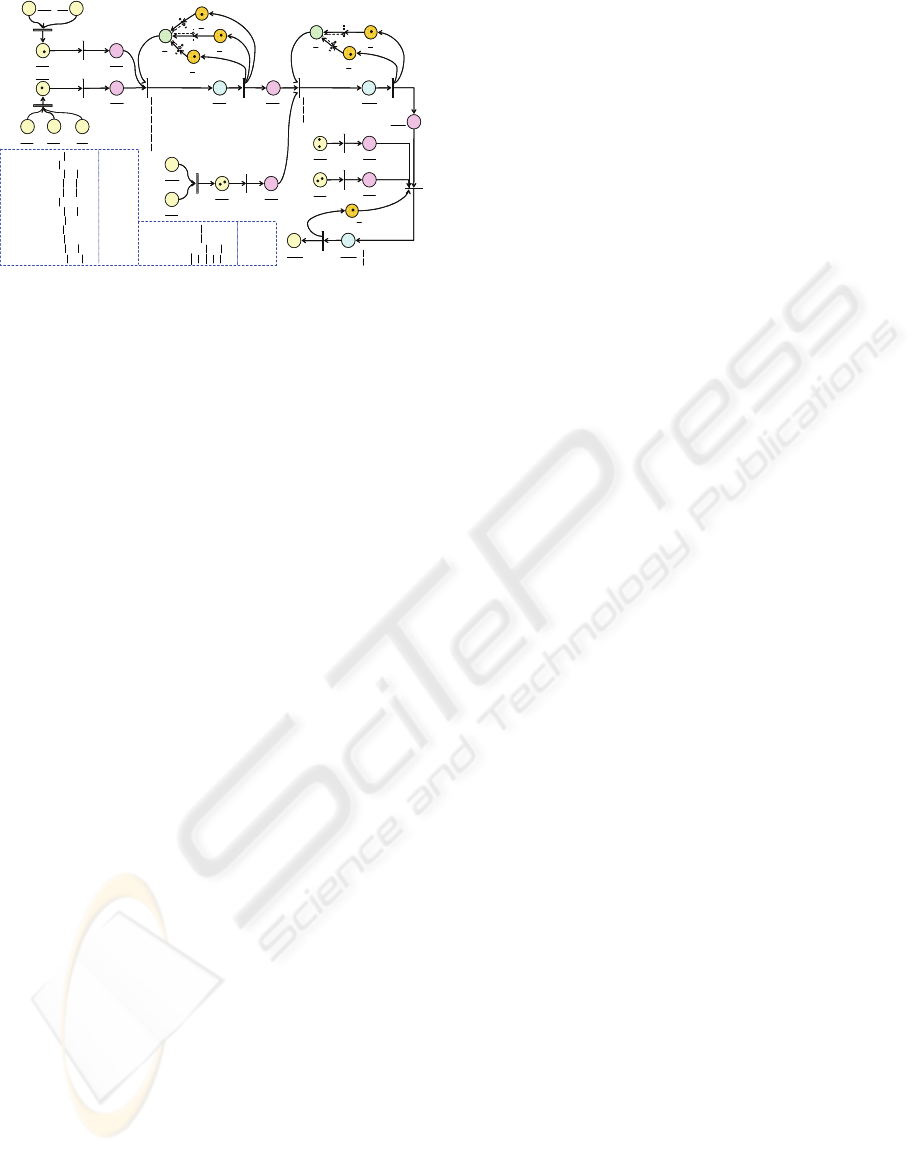
similar way, by following the common process flow

in assembling final motors, the

PNet for the motor

family is constructed, as shown in Fig. 6. The places

and represented system elements are given in Table

1.

5 SYSTEM OF HCTPNS

While MNets , ANets and

PNets

are to model the

processes of component parts, assemblies and end-

products, where only the immediate child items are

considered, a multilevel hierarchical net system is

defined to capture and model the complete

production processes of a product family.

A PETRI NET MODEL OF PROCESS PLATFORM-BASED PRODUCTION CONFIGURATION

9

21

CACAwithFCAcoltype =

321

BbBbBbwithFBbcoltype =

654321

mmmmmmwithRcoltype =

FCAxvar

1

:

FAAxvar

3

:

Rrvar :

21

StStwithFStcoltype =

21

TlTlwithFTlcoltype =

321

AAAAAAwithFAAcoltype =

321

BABABAwithFBAcoltype =

321

BaBaBawithFBacoltype =

FStxvar

2

:

FBbyvar

2

:

FBayvar

1

:

21

FmFmwithFFmcoltype =

FTlyvar

3

:

FBAyvar

4

:

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

321

ABABABwithFABcoltype =

21

MtMtwithFMtcoltype =

321

MBMBMBwithFMBcoltype =

21

FAFAwithFFAcoltype =

21

WtWtwithFWtcoltype =

321

VMVMVMwithFVMcoltype =

21

RhRhwithFRhcoltype =

FFmzvar

1

:

FFAzvar

3

:

FMtzvar

2

:

FABxvar

4

:

FWtxvar

6

:

FMBxvar

5

:

FVMxvar

8

:

FRhxvar

7

:

1

x

2

x

3

x

3

x

3

x

3

x

1

y

2

y

3

y

4

y

4

y

4

y

4

y

4

x

4

x

4

x

r

1

m

2

m

3

m

1

m

2

m

3

m

1

m

2

m

3

m

12@ABm,BA,AA

9@ABm,BA,AA

13@ABm,BA,AA

11@ABm,BA,AA

15@ABm,BA,AA

12@ABm,BA,AA

10@ABm,BA,AA

ofr,y,xcase

3333

3233

2322

2122

1311

1211

1111

43

+→

5

x

7.11@MBm,FA,AB

6.10@MBm,FA,AB

2.14@MBm,FA,AB

8.12@MBm,FA,AB

ofr,z,xcase

3423

2522

1511

1411

34

+→

5

x

8.7@VMm,Rh,Wt,MB

7.6@VMm,Rh,MB

2.6@VMm,Wt,MB

ofm,x,x,xcase

16111

3623

2622

6765

+→

4

m

5

m

4

m

5

m

4

m

5

m

6

x

7

x

6

x

7

x

6

x

7

x

5

x

6

m

8

x

8

x

6

m

1

z

2

z

3

z

3

z

3

z

3

z

21

CACAwithFCAcoltype =

321

BbBbBbwithFBbcoltype =

654321

mmmmmmwithRcoltype =

FCAxvar

1

:

FAAxvar

3

:

Rrvar :

21

StStwithFStcoltype =

21

TlTlwithFTlcoltype =

321

AAAAAAwithFAAcoltype =

321

BABABAwithFBAcoltype =

321

BaBaBawithFBacoltype =

FStxvar

2

:

FBbyvar

2

:

FBayvar

1

:

21

FmFmwithFFmcoltype =

FTlyvar

3

:

FBAyvar

4

:

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

321

ABABABwithFABcoltype =

21

MtMtwithFMtcoltype =

321

MBMBMBwithFMBcoltype =

21

FAFAwithFFAcoltype =

21

WtWtwithFWtcoltype =

321

VMVMVMwithFVMcoltype =

21

RhRhwithFRhcoltype =

FFmzvar

1

:

FFAzvar

3

:

FMtzvar

2

:

FABxvar

4

:

FWtxvar

6

:

FMBxvar

5

:

FVMxvar

8

:

FRhxvar

7

:

1

x

2

x

3

x

3

x

3

x

3

x

1

y

2

y

3

y

4

y

4

y

4

y

4

y

4

x

4

x

4

x

r

1

m

2

m

3

m

1

m

2

m

3

m

1

m

2

m

3

m

12@ABm,BA,AA

9@ABm,BA,AA

13@ABm,BA,AA

11@ABm,BA,AA

15@ABm,BA,AA

12@ABm,BA,AA

10@ABm,BA,AA

ofr,y,xcase

3333

3233

2322

2122

1311

1211

1111

43

+→

5

x

7.11@MBm,FA,AB

6.10@MBm,FA,AB

2.14@MBm,FA,AB

8.12@MBm,FA,AB

ofr,z,xcase

3423

2522

1511

1411

34

+→

5

x

8.7@VMm,Rh,Wt,MB

7.6@VMm,Rh,MB

2.6@VMm,Wt,MB

ofm,x,x,xcase

16111

3623

2622

6765

+→

4

m

5

m

4

m

5

m

4

m

5

m

6

x

7

x

6

x

7

x

6

x

7

x

5

x

6

m

8

x

8

x

6

m

1

z

2

z

3

z

3

z

3

z

3

z

Figure 6: The PNet of the motor family.

A hierarchical colored timed PN (

HCTPN

) is

defined as a tuple,

(

)

HRTagsPPSPSTNETHCTPN

r

,,,,,,,,

χγϖβ

=

, where

•

MNetsANetsPNetNET ∪∪=

is a finite

nonempty set of nets with 3 disjoint subsets: a

PNet

, a set of

ANets

and a set of

MNets

such that

NETNetNet

ji

∈≠∀

:

φ

=∩

ji

NetNet

;

•

r

ANet

r

ANet

r

PNet

r

n1

TTTST ∪∪= "

is a finite

nonempty set of refinement transitions with n+1

disjoint subsets: a set of refinement transitions of

the

PNet

and

n

disjoint sets of refinement transitions

of the corresponding

ANets

;

•

NETST

r

6:

β

is a net assignment function

that maps

r

ST

into

NET

such that

j

r

NetSTt ∩∈∀

NETsNetNet

ji

∈≠∀

:

()

i

Nett =

β

;

•

SP

is a finite nonempty set of socket places

such that

NETNetSTtSPp

i

r

∈∀∈∀∈∀

:

∧∈

i

Nett,p

(

)

••

∈∨∈ tptp

;

•

{}

Out/In,Out,InSP 6:

ϖ

is a socket type

function that maps a socket place to either an input

type, output type, or input/output type;

•

PP

is a finite nonempty set of port places such

that

r

ii

STtNetPPpNETNet ∈∀∩∈∀∈∀

:

()

i

Nett =

β

;

•

{}

Out/In,Out,InPP 6:

γ

is a port type

function that maps each port place to either an input

type, output type, or input/output type;

•

PPSPST

r

×: 6

χ

is a port assignment

function that maps each refinement transition to a

binary relation between a socket place and a port

place such that

(

)

()

(

)

(

)

()

(

)

jijiji

r

pppptp,pSTt

ααγϖχ

=∧=:∈∀∈∀

;

•

HRTags

is a set of hierarchical refinement tags

that are defined for

r

ST

.

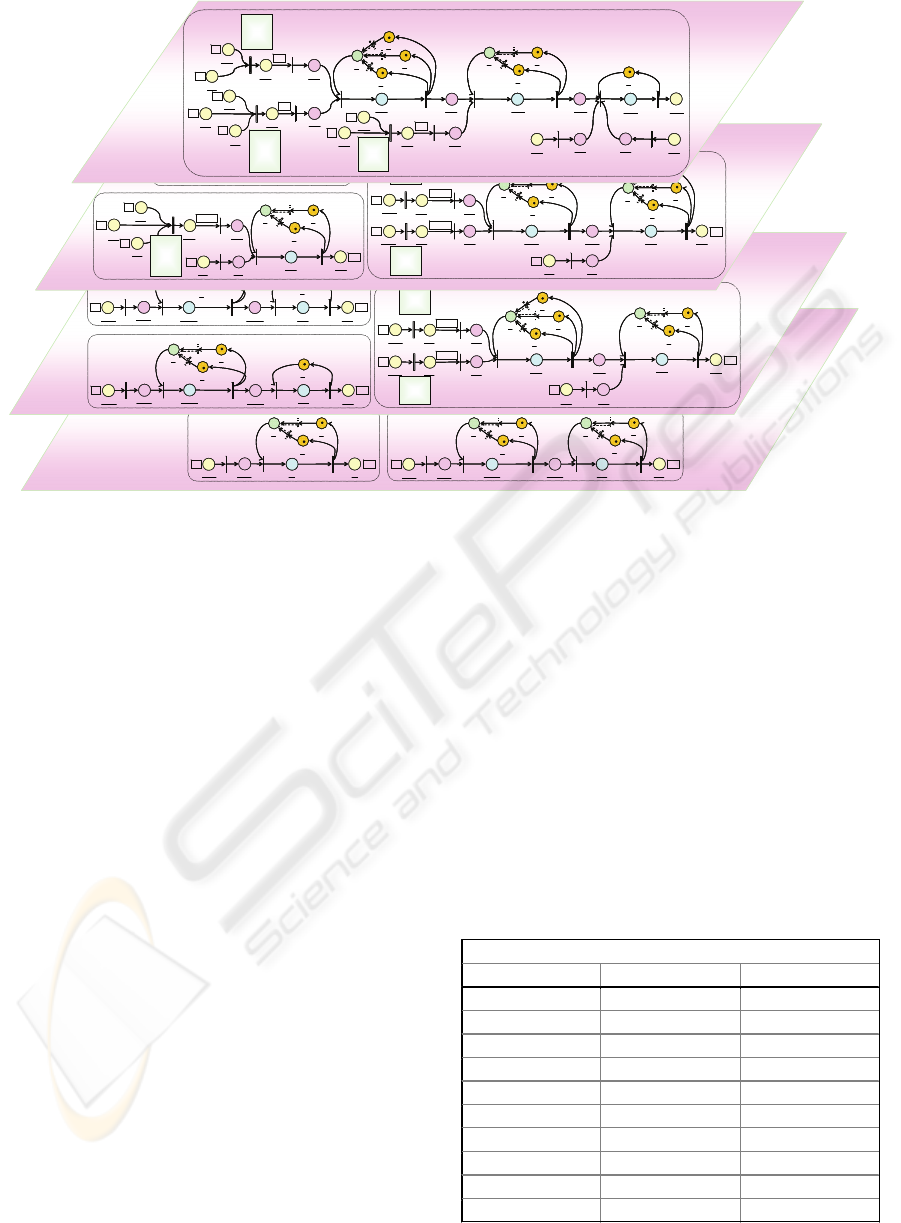
Based on the above definition and the

constructed

PNet , ANets and MNets , the HCTPN

shown in Fig. 7 has been constructed to model the

configuration of complete production processes of

vibration motors. Also shown are

HRTags

defined

for refinement transitions, socket and port places,

types of socket and port places.

Since port places of an output type on

MNets and

ANets at lower levels contain colored tokens

representing material items involved in

ANets at

higher levels, an

HCTPN evolves in a bottom-up

manner. More specifically,

MNets at the lowest

level of each branch evolve first. Transition firing in

these

MNets leads to the generation of colored

tokens representing produced parts in the output port

places. At the same time, these colored tokens are

generated in the corresponding output socket places

on

ANets at higher levels as well. With the presence

of these colored tokens together with others

representing available machines, purchased parts

and/or assemblies, transitions on the immediate

higher level

ANets will be enabled and thus fire,

which generates colored tokens representing

produced assemblies in the output port places on the

ANets . Such colored tokens will appear

simultaneously in the corresponding socket places

on the

ANets of parent assemblies, and so on. This

process continues till the

PNe

t

at the top level has

been reached.

6 APPLICATION RESULTS

6.1 Model Analysis

After construction, all net models are analyzed to

determine whether or not they logically reflect

system operations. In the literature, P-invariant

analysis is often adopted by researchers to analyze

their PN models due to its analysis advantages

(Jensen, 1997). In this study, we, thus, adopt P-

invariant analysis as well. Several P-invariants are

identified in each

MNet , ANet and the PNet . The

total number of busy machines and idle machines

leads to a P-invariant. Another P-invariant relates to

items in buffer places, items ready to be processed

and items being processed (represented by items to

be produced).

Moreover, in view of the fact that deadlocks and

conflicts have a major impact on the operations of

system models, we conduct deadlock and conflict

analysis as well. Among the several types of

conflicts, conflicts that may result from resources

sharing do not exist in the constructed net models.

ICEIS 2009 - International Conference on Enterprise Information Systems

10

1

P

2

P

4

P

7

P

3

P

5

P

6

P

1

t

5

t

2

t

4

t

3

t

R

FRCl

Cl

OutIn

Cl_MNet

FRCl

Cl

1

P

2

P

4

P

7

P

3

P

9

P

12

P

5

P

6

P

1

t

6

t

5

t

2

t

9

t

4

t

3

t

FRCt

1FCt ⋅ FCt

R

OutIn

Ct_MNet

8

P

10

P

11

P

8

t

7

t

R

FRCt

1FCt ⋅ FCt

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBb

1FBb⋅ FBb

R R

R

FRBb

1FBb⋅ FBb

OutIn

Bb_MNet

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRCl

11

t

12

t

14

t

7

t

6

t

9

t

FCt

FRCt

FCl

FCtl

FTp

FCA

R

CA_ANet

FCt

FCl

FCtl

FTp

FCA

Out/In

In

Out/In

In

Out

122

11

7

pp

Ct_MNet

HRTag

→

75

14

8

pp

Cl_MNet

HRTag

→

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBa

1FBa ⋅

FBa

R

FRBa

1FBa ⋅ FBa

OutIn

Ba_MNet

1

P

2

P

4

P

5

P

3

P

6

P

8

P

7

P

9

P

3

t

2

t

1

t

5

t

4

t

FMt

6

t

FFm

FFA

R

FA_ANet

FMt

FFm

FFA

In

Out

1

P

4

P

6

P

5

P

7

P

8

P

11

P

12

P

9

P

10

P

3

t

1

t

8

t

5

t

4

t

7

t

6

t

FCA

FCt

FSt

FAA

R

FAA

AA_ANet

FCl

FTp

2

P

3

P

FCA

FSt

Out/In

Out

In

194

133

52

21

6

pp

CA_ANet

HRTag

→

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRBb

11

t

12

t

14

t

7

t

6

t

9

t

FBa

FRBa

FBb

FBab

FTl

FBA

R

FBa

FBb

FBab

FTl

FBA

BA_ANet

Out/In

Out

102

11

4

pp

Ba_MNet

HRTag

→

In

Out/In

In

105

14

5

pp

Bb_MNet

HRTag

→

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa

FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

R R

R

In

Out

123

62

41

1

pp

AA_ANet

HRTag

→

In

Out

In

Out

In

194

127

56

25

2

pp

BA_ANet

HRTag

→

918

317

116

3

pp

FA_ANet

HRTag

→

PNet

1

P

2

P

4

P

7

P

3

P

5

P

6

P

1

t

5

t

2

t

4

t

3

t

R

FRCl

Cl

OutIn

Cl_MNet

FRCl

Cl

1

P

2

P

4

P

7

P

3

P

5

P

6

P

1

t

5

t

2

t

4

t

3

t

R

FRCl

Cl

OutIn

Cl_MNet

FRCl

Cl

1

P

2

P

4

P

7

P

3

P

5

P

6

P

1

t

5

t

2

t

4

t

3

t

R

FRCl

Cl

OutOutInIn

Cl_MNet

FRCl

Cl

1

P

2

P

4

P

7

P

3

P

9

P

12

P

5

P

6

P

1

t

6

t

5

t

2

t

9

t

4

t

3

t

FRCt

1FCt ⋅ FCt

R

OutIn

Ct_MNet

8

P

10

P

11

P

8

t

7

t

R

FRCt

1FCt ⋅ FCt

1

P

2

P

4

P

7

P

3

P

9

P

12

P

5

P

6

P

1

t

6

t

5

t

2

t

9

t

4

t

3

t

FRCt

1FCt ⋅ FCt

R

OutIn

Ct_MNet

8

P

10

P

11

P

8

t

7

t

R

FRCt

1FCt ⋅ FCt

1

P

2

P

4

P

7

P

3

P

9

P

12

P

5

P

6

P

1

t

6

t

5

t

2

t

9

t

4

t

3

t

FRCt

1FCt ⋅ FCt

R

OutOutInIn

Ct_MNet

8

P

10

P

11

P

8

t

7

t

R

FRCt

1FCt ⋅ FCt

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBb

1FBb⋅ FBb

R R

R

FRBb

1FBb⋅ FBb

OutIn

Bb_MNet

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBb

1FBb⋅ FBb

R R

R

FRBb

1FBb⋅ FBb

OutIn

Bb_MNet

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBb

1FBb⋅ FBb

R R

R

FRBb

1FBb⋅ FBb

OutIn

Bb_MNet

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRCl

11

t

12

t

14

t

7

t

6

t

9

t

FCt

FRCt

FCl

FCtl

FTp

FCA

R

CA_ANet

FCt

FCl

FCtl

FTp

FCA

Out/In

In

Out/In

In

Out

122

11

7

pp

Ct_MNet

HRTag

→

75

14

8

pp

Cl_MNet

HRTag

→

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRCl

11

t

12

t

14

t

7

t

6

t

9

t

FCt

FRCt

FCl

FCtl

FTp

FCA

R

CA_ANet

FCt

FCl

FCtl

FTp

FCA

Out/In

In

Out/In

In

Out

122

11

7

pp

Ct_MNet

HRTag

→

75

14

8

pp

Cl_MNet

HRTag

→

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRCl

11

t

12

t

14

t

7

t

6

t

9

t

FCt

FRCt

FCl

FCtl

FTp

FCA

R

CA_ANet

FCt

FCl

FCtl

FTp

FCA

Out/In Out/In

InIn

Out/In Out/In

InIn

OutOut

122

11

7

pp

Ct_MNet

HRTag

→

122

11

7

pp

Ct_MNet

HRTag

→

75

14

8

pp

Cl_MNet

HRTag

→

75

14

8

pp

Cl_MNet

HRTag

→

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBa

1FBa ⋅

FBa

R

FRBa

1FBa ⋅ FBa

OutIn

Ba_MNet

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBa

1FBa ⋅

FBa

R

FRBa

1FBa ⋅ FBa

OutIn

Ba_MNet

1

P

2

P

4

P

7

P

8

P

3

P

9

P

10

P

5

P

6

P

1

t

6

t

5

t

2

t

7

t

4

t

3

t

FRBa

1FBa ⋅

FBa

R

FRBa

1FBa ⋅ FBa

OutOutInIn

Ba_MNet

1

P

2

P

4

P

5

P

3

P

6

P

8

P

7

P

9

P

3

t

2

t

1

t

5

t

4

t

FMt

6

t

FFm

FFA

R

FA_ANet

FMt

FFm

FFA

In

Out

1

P

2

P

4

P

5

P

3

P

6

P

8

P

7

P

9

P

3

t

2

t

1

t

5

t

4

t

FMt

6

t

FFm

FFA

R

FA_ANet

FMt

FFm

FFA

In

Out

1

P

2

P

4

P

5

P

3

P

6

P

8

P

7

P

9

P

3

t

2

t

1

t

5

t

4

t

FMt

6

t

FFm

FFA

R

FA_ANet

FMt

FFm

FFA

InIn

OutOut

1

P

4

P

6

P

5

P

7

P

8

P

11

P

12

P

9

P

10

P

3

t

1

t

8

t

5

t

4

t

7

t

6

t

FCA

FCt

FSt

FAA

R

FAA

AA_ANet

FCl

FTp

2

P

3

P

FCA

FSt

Out/In

Out

In

194

133

52

21

6

pp

CA_ANet

HRTag

→

1

P

4

P

6

P

5

P

7

P

8

P

11

P

12

P

9

P

10

P

3

t

1

t

8

t

5

t

4

t

7

t

6

t

FCA

FCt

FSt

FAA

R

FAA

AA_ANet

FCl

FTp

2

P

3

P

FCA

FSt

Out/In

Out

In

194

133

52

21

6

pp

CA_ANet

HRTag

→

1

P

4

P

6

P

5

P

7

P

8

P

11

P

12

P

9

P

10

P

3

t

1

t

8

t

5

t

4

t

7

t

6

t

FCA

FCt

FSt

FAA

R

FAA

AA_ANet

FCl

FTp

2

P

3

P

FCA

FSt

Out/In Out/In

OutOut

InIn

194

133

52

21

6

pp

CA_ANet

HRTag

→

194

133

52

21

6

pp

CA_ANet

HRTag

→

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRBb

11

t

12

t

14

t

7

t

6

t

9

t

FBa

FRBa

FBb

FBab

FTl

FBA

R

FBa

FBb

FBab

FTl

FBA

BA_ANet

Out/In

Out

102

11

4

pp

Ba_MNet

HRTag

→

In

Out/In

In

105

14

5

pp

Bb_MNet

HRTag

→

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRBb

11

t

12

t

14

t

7

t

6

t

9

t

FBa

FRBa

FBb

FBab

FTl

FBA

R

FBa

FBb

FBab

FTl

FBA

BA_ANet

Out/In

Out

102

11

4

pp

Ba_MNet

HRTag

→

In

Out/In

In

105

14

5

pp

Bb_MNet

HRTag

→

1

P

2

P

4

P

5

P

3

P

6

P

8

P

11

P

14

P

16

P

17

P

12

P

13

P

18

P

7

P

15

P

19

P

9

P

10

P

3

t

2

t

1

t

10

t

8

t

13

t

5

t

4

t

FRBb

11

t

12

t

14

t

7

t

6

t

9

t

FBa

FRBa

FBb

FBab

FTl

FBA

R

FBa

FBb

FBab

FTl

FBA

BA_ANet

Out/In

OutOut

102

11

4

pp

Ba_MNet

HRTag

→

102

11

4

pp

Ba_MNet

HRTag

→

InIn

Out/In Out/In

InIn

105

14

5

pp

Bb_MNet

HRTag

→

105

14

5

pp

Bb_MNet

HRTag

→

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa

FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

R R

R

In

Out

123

62

41

1

pp

AA_ANet

HRTag

→

In

Out

In

Out

In

194

127

56

25

2

pp

BA_ANet

HRTag

→

918

317

116

3

pp

FA_ANet

HRTag

→

PNet

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa

FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

R R

R

In

Out

123

62

41

1

pp

AA_ANet

HRTag

→

In

Out

In

Out

In

194

127

56

25

2

pp

BA_ANet

HRTag

→

918

317

116

3

pp

FA_ANet

HRTag

→

PNet

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa

FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

R R

R

In

Out

123

62

41

1

pp

AA_ANet

HRTag

→

In

Out

In

Out

In

194

127

56

25

2

pp

BA_ANet

HRTag

→

918

317

116

3

pp

FA_ANet

HRTag

→

1

P

3

P

5

P

4

P

8

P

9

P

11

P

15

P

2

P

6

P

7

P

10

P

12

P

13

P

18

P

19

P

14

P

17

P

20

P

21

P

24

P

25

P

30

P

31

P

16

P

22

P

23

P

26

P

29

P

3

t

2

t

1

t

10

t

12

t

9

t

8

t

18

t

19

t

5

t

4

t

FCA

6

t

7

t

15

t

16

t

14

t

13

t

11

t

FSt

FAA

FBa

FTl

FFm

FBA

FBb

FMt

FAB

FFA

FMB

FVM

FAA

FBA

FFA

FVM

FAB

FMB

FWt

27

P

28

P

17

t

FRh

R

R R

R

InIn

OutOut

123

62

41

1

pp

AA_ANet

HRTag

→

123

62

41

1

pp

AA_ANet

HRTag

→

In

OutOut

InIn

OutOut

InIn

194

127

56

25

2

pp

BA_ANet

HRTag

→

194

127

56

25

2

pp

BA_ANet

HRTag

→

918

317

116

3

pp

FA_ANet

HRTag

→

918

317

116

3

pp

FA_ANet

HRTag

→

PNet

Figure 7: The HCTPN modeling PPbPC of the motor family.

The definitions of colored tokens and arc

expressions have resolved the possible conflicts in

relation to transition firing with respect to different

colored tokens and time durations. Thus, no conflicts

exist in

MNets , ANets and the PNet . For analyzing

deadlocks, we adopt the Deadlock Detection

Algorithm (DDA) (Wang and Wu, 1998). For any

given initial state of each

MNet , ANet and the

PNet in the HCTPN , a goal state is always obtained

using the DDA. This concludes that the

HCTPN is

deadlock free.

6.2 Application Results

The HCTPN in Fig. 7 is applied to the three

vibration motors:

,VM

1

2

VM and

3

VM . The

selection of alternative machines and production

processes is based on the minimal completion time

of the three vibration motors. The rule to fire

transitions is the shortest delay times. The results are

three production processes, more specifically all

machines required to produce

21

VM,VM and

3

VM .

Table 2 lists these machines. The indices of

machines are applicable to machines in the

corresponding manufacturing/assembly processes of

product items, and thus machines with same indices

producing different product items are not the same.

Due to space constraints, not all of the machines are

shown in the table.

7 CONCLUSIONS

Recognizing the significance of PPbPC in achieving

production efficiency of product families, we

presented a holistic model of PPbPC. A formalism

of HCTPNs was proposed to facilitate modeling

PPbPC by integrating the basic principles of HPNs,

TPNs and CPNs. The industrial example has proven

the feasibility and potential of using HCTPNs to

model PPbPC. Future research may be directed to

develop a computational system based on the

proposed formalism to implement PPbPC.

Table 2: The configured production processes for the three

motor variants.

Machine(Operation; Product item)

1

VM

2

VM

3

VM

2

m

(Manufacturing operation;

1Ba

1

⋅

)

2

m

(Manufacturing operation;

1Ba

2

⋅

)

1

m

(Manufacturing operation;

1Ba

3

⋅

)

3

m

(Manufacturing operation;

1

Ba

)

3

m

(Manufacturing operation;

2

Ba

)

3

m

(Manufacturing operation;

3

Ba

)

2

m

(Manufacturing operation;

1Bb

1

⋅

)

1

m

(Manufacturing operation;

1Bb

2

⋅

)

2

m

(Manufacturing operation;

1Bb

3

⋅

)

3

m

(Manufacturing operation;

1

Bb

)

3

m

(Manufacturing operation;

2

Bb

)

3

m

(Manufacturing operation;

3

Bb

)

… … …

2

m

(Assembly operation;

1

AA

)

1

m

( Assembly operation;

2

AA

)

2

m

( Assembly operation;

1

AA

)

1

m

(Assembly operation;

1

FA

)

2

m

( Assembly operation;

2

FA

)

1

m

( Assembly operation;

3

FA

)

1

m

(Assembly operation;

1

AB

)

3

m

( Assembly operation;

2

AB

)

2

m

( Assembly operation;

3

AB

)

5

m

(Assembly operation;

1

MB

)

5

m

(Assembly operation;

2

MB

)

4

m

(Assembly operation;

3

MB

)

6

m

(Assembly operation;

1

VM

)

6

m

(Assembly operation;

2

VM

)

6

m

(Assembly operation;

3

VM

)

A PETRI NET MODEL OF PROCESS PLATFORM-BASED PRODUCTION CONFIGURATION

11

REFERENCES

Bley, H., Zenner, C., 2006. Variant-oriented assembly

planning.

Annals of the CIRP, 55, pp. 23-28.

Cortes, L.A., Eles, P., Peng, Z., 2003. Modeling and

formal verification of embedded systems based on a

Petri net representation.

Journal of Systems

Architecture

, 49, pp. 571-598.

Dussart, A., Aubert, B.A., Patry, M., 2004. An evaluation

of inter-organizational workflow modeling

formalisms.

Journal of Database Management, 15, pp.

74-104.

EIMaraghy, H.A., 2006. Flexible and reconfigurable

manufacturing systems paradigms.

Annals of the

CIRP

, 56, pp. 467-472.

EIMaraghy, H.A., 2007. Mathematical modelling for

reconfigurable process planning. International Journal

of Flexible Manufacturing Systems

, 17, pp. 261-276.

Fehling, R., 1993. A concept of hierarchical Petri nets

with building blocks. in

Advances in Petri nets

(Rozenberg, G., Ed.), vol. 674 of Lecture Notes in

Computer Science, Springer-Verlang, pp. 148-168.

Jensen, K., 1997. Colored Petri nets: basic concepts,

analysis methods and practical use. Vol. 2, New York:

Springer.

Jiao, J., Zhang, L., Zhang, Y., Pokharel, S., 2008.

Association rule mining for product and process

variety mapping. International Journal of Computer

Integrated Manufacturing

, 21, pp. 111-124.

Ramachandani, C., 1974. Analysis of asynchronous

concurrent systems by timed Petri nets. Technical

Report MAC TR 120, MIT, Cambridge.

Schierholt, K., 2001. Process configuration: combining the

principles of product configuration and process

planning. Artificial Intelligence for Engineering

Design, Analysis and Manufacturing

, 15, pp. 411–424.

Silva, S.C., Alves, A. C., 2006. Detailed design of product

oriented manufacturing systems, The International

Conference on Group Technology/Cellular

Manufacturing

, Groningen, The Netherlands.

Wang, L.C., Wu, S.Y., 1998. Modeling with colored timed

object-oriented Petri nets for automated

manufacturing systems.

Computers & Industrial

Engineering

, 34, pp. 463-480.

WiendahI, H.-P., EIMaraghy, H.A., Nyhuis, P., Zah, M.F.,

WiendahI, H.-H., Duffie, N., Brieke, M., 2007.

Changeable manufacturing – classification, design and

operation.

Annals of the CIRP, 56, pp. 783-8029.

Williams, C.B., Allen, J.K., Rosen, D.W., Mistree, F.,

2007. Designing platforms for customizable products

and processes in markets of non-uniform demand.

Current Engineering: Research and Applications, 15,

pp. 201-216.

Zhang, L., 2007. Process platform-based production

configuration for mass customization. PhD

Dissertation, Division of Systems and Engineering

Management, Nanyang Technological University,

Singapore.

Zhang, L., Jiao, J., Helo, P.T., 2007. Process platform

representation based on unified modeling language.

International Journal of Production Research, 45, pp.

323-350.

ICEIS 2009 - International Conference on Enterprise Information Systems

12