ARTICULATED HUMAN MOTION TRACKING WITH HPSO
Vijay John, Spela Ivekovic
School of Computing, University of Dundee, Dundee, U.K.
Emanuele Trucco
School of Computing, University of Dundee, Dundee, U.K.
Keywords:
Articulated human motion tracking, Hierarchical particle swarm optimisation, Annealed particle filter.
Abstract:
In this paper, we address full-body articulated human motion tracking from multi-view video sequences ac-
quired in a studio environment. The tracking is formulated as a multi-dimensional nonlinear optimisation and
solved using particle swarm optimisation (PSO), a swarm-intelligence algorithm which has gained popularity
in recent years due to its ability to solve difficult nonlinear optimisation problems. Our tracking approach is
designed to address the limits of particle filtering approaches: it initialises automatically, removes the need
for a sequence-specific motion model and recovers from temporary tracking divergence through the use of a
powerful hierarchical search algorithm (HPSO). We quantitatively compare the performance of HPSO with
that of the particle filter (PF) and annealed particle filter (APF). Our test results, obtained using the framework
proposed by (Balan et al., 2005) to compare articulated body tracking algorithms, show that HPSO’s pose
estimation accuracy and consistency is better than PF and compares favourably with the APF, outperforming
it in sequences with sudden and fast motion.
1 INTRODUCTION
Tracking articulated human motion from video se-
quences is an important problem in computer vision
with applications in virtual character animation, med-
ical posture analysis, surveillance, human-computer
interaction and others. In this paper, we formulate the
full-body articulated tracking as a nonlinear optimi-
sation problem which we solve using particle swarm
optimization (PSO), a recent swarm intelligence algo-
rithm with growing popularity (Poli, 2007; Poli et al.,
2008).
Because the full-body articulated pose estimation
is a high-dimensional optimisation problem, we for-
mulate it as a hierarchical PSO algorithm (HPSO)
which exploits the inherent hierarchy of the human-
body kinematic model, thus reducing the computa-
tional complexity of the search.
HPSO is designed to address the limits of the par-
ticle filtering approaches. Firstly, it removes the need
for a sequence-specific motion model: the same al-
gorithm with unmodified parameter settings is able
to track different motions without any prior knowl-
edge of the motion’s nature. Secondly, it addresses
the problem of divergence, a characteristic behaviour
of particle filter implementations, whereby the filter
loses track after a wrongly estimated pose and is un-
able to recover unless interactively corrected by the
user or assisted by additional, higher-level motion
models (Caillette et al., 2008). In contrast, our track-
ing approach is able to automatically recover from an
incorrect pose estimate and continue tracking. Last
but not least, in line with its ability to recover from
an incorrect pose estimate, our HPSO tracker also
initialises automatically on the first frame of the se-
quence, requiring no manual intervention.
This paper is organised as follows. We describe
the related work in Section 2. Section 3 presents the
PSO algorithm. In Section 4 we describe the body
model and cost function used in our tracking approach
and in Section 5 present the HPSO algorithm. We
show the experimental results including a comparison
of our algorithm with the particle filter (PF) and the
annealed particle filter (APF) in Section 6. Section 7
contains conclusions and ideas for future work.
531
John V., Ivekovic S. and Trucco E. (2009).
ARTICULATED HUMAN MOTION TRACKING WITH HPSO.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 531-538
DOI: 10.5220/0001804505310538
Copyright
c
 SciTePress

2 RELATED WORK
The approaches to articulated motion analysis can
generally be divided into generative and discrimi-
native methods. The generative methods use the
analysis-by-synthesis approach, where the candidate
pose is represented by an explicit body model and the
appropriate likelihood function is evaluated to deter-
mine its fitness. The discriminative methods, on the
other hand, represent the articulated pose implicitly
by learning the mapping between the pose space and
a set of image features. Combinations of both ap-
proaches have also been reported.
Our method fits under the umbrella of generative
analysis-by-synthesis and we review the related work
accordingly. We do not attempt to provide an ex-
haustive list of related research and instead refer the
reader to one of the many recent surveys on this topic
(Poppe, 2007).
As articulated pose estimation is a high-
dimensional search problem, particle filtering ap-
proaches, with their ability to use non-linear motion
models and explore the search space with a num-
ber of different hypotheses, have become very pop-
ular. An early attempt was the Condensation algo-
rithm (Isard and Blake, 1998), which in its origi-
nal form quickly became computationally unfeasible
when applied to high-dimensional problem of articu-
lated tracking (Deutscher and Reid, 2005).
Efforts to reduce the computational complexity
and the required number of particles resulted in var-
ious extensions, some focusing on ways of partition-
ing the search space or modifying the sampling pro-
cess (MacCormick and Isard, 2000; Sminchisescu
and Triggs, 2003; Husz et al., 2007) and others ad-
vocating trained prior models (Vondrak et al., 2008;
Caillette et al., 2008).
In our work, we also formulate the pose estima-
tion as a hierarchical search problem, thereby parti-
tioning the search space to reduce the computational
complexity of the search, however, instead of using
a particle filter to estimate the pose, we employ a
powerful swarm intelligence global search algorithm,
called particle swarm optimisation (PSO) (Kennedy
and Eberhart, 1995). Similarly to the annealed par-
ticle filter (APF) and its genetic crossover extension
(Deutscher and Reid, 2005), the idea is to allow the
particles to explore the search space for a number of
iterations per frame. The advantageof our method lies
in the way the particles communicate with each other
to find the optimum. Our method does not use any
motion priors and we are able to demonstrate experi-
mentally that our approach outperforms the APF with
crossover operator by (Deutscher and Reid, 2005).
PSO is a swarm intelligence search technique
which has been growing in popularity and has in the
past 13 years been used to solve various non-linear
optimisation problems in a number of areas, includ-
ing computer vision (Poli, 2007). A recent publica-
tion by (Zhang et al., 2008) demonstrated an applica-
tion of a variant of PSO, called sequential PSO, to box
tracking in video sequences and theoretically demon-
strated that their framework in essence represented a
multi-layer importance sampling based particle filter.
Applications of PSO to articulated pose estimation
from multi-view still images have also been reported
(Ivekovic and Trucco, 2006; Ivekovic et al., 2008), as
well as articulated tracking from stereo data (Robert-
son et al., 2005; Robertson and Trucco, 2006).
The work reported in this paper is an extension
of (Ivekovic and Trucco, 2006; Ivekovic et al., 2008)
to full-body pose estimation from multi-view video
sequences.
3 PARTICLE SWARM
OPTIMISATION
Particle swarm optimisation (PSO) is a swarm intel-
ligence technique introduced by (Kennedy and Eber-
hart, 1995). The idea originated from the simulation
of a simplified social model, where the agents were
thought of as collision-proof birds and the original
intent was to graphically simulate the unpredictable
choreography of a bird flock in their search for food.
The original PSO algorithm was later modified by
several researchers to improve its search capabilities
and convergence properties. In this paper we use the
PSO algorithm with an inertia weight parameter, in-
troduced by (Shi and Eberhart, 1998).
3.1 PSO Algorithm with Inertia Weight
Parameter
Assume an n-dimensional search space S ⊆ R
n
, a
swarm consisting of N particles, each particle rep-
resenting a candidate solution to the search prob-
lem, and a cost function f : S → R defined on the
search space. The i-th particle is represented as an n-
dimensional vector x
i
= (x
1
,x
2
,...,x
n
)
T
∈ S. The ve-
locity of this particle is also an n-dimensional vector
v
i
= (v
1
,v
2
,...,v
n
)
T
∈ S. The best position encoun-
tered by the i-th particle so far (personal best) is de-
noted by p
i
= (p
1
, p
2
,..., p
n
)
T
∈ S and the value of
the cost function at that position pbest
i
= f (p
i
). The
index of the particle with the overall best position so
far (global best) is denoted by g and gbest = f (p
g
).
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
532

The PSO algorithm can then be stated as follows:
1. Initialisation:
• Initialise a population of particles {x
i
},i =
1...N, with random positions and velocities in
the search space S. For each particle evaluate
the desired cost function f and set pbest
i
=
f(x
i
). Identify the best particle in the swarm
and store its index as g and its position as p
g
.
2. Repeat until the stopping criterion is fulfilled:
• Move the swarm by updating the position of ev-
ery particle x
i
, i = 1...N, according to the fol-
lowing two equations:
v
i
t+1
= wv
i
t
+ ϕ
1
(p
i
t
− x
i
t
) + ϕ
2
(p
g
t
− x
i
t
)
x
i
t+1
= x
i
t
+ v
i
t+1
(1)
where subscript t denotes the time step (itera-
tion).
• For i = 1. . . N update p
i
, pbest
i
, p
g
and gbest.
The stopping criterion is usually either the maximum
number of iterations or the minimum gbest improve-
ment. The parameters ϕ
1
= c
1
rand
1
() and ϕ
2
=
c
2
rand
2
(), where c is a constant and rand() is a ran-
dom number drawn from [0,1], influence the social
and cognition components of the swarm behaviour,
respectively. In line with (Kennedy and Eberhart,
1995), we set c
1
= c
2
= 2, which gives the stochas-
tic factor a mean of 1.0 and causes the particles to
”overfly” the target about half of the time, while also
giving equal importance to both social and cognition
components. Parameter w is the inertia weight which
we describe in more detail next.
3.2 Inertia Weight Parameter
The inertia weight w can remain constant throughout
the search or change with time. It plays an impor-
tant role in directing the exploratory behaviour of the
particles: higher inertia values push the particles to
explore more of the search space and emphasise their
individual velocity, while lower inertia values force
particles to focus on a smaller search area and move
towards the best solution found so far.
In this paper, we use a time-varying inertia
weight.We model the change over time with an ex-
ponential function which allows us to use a constant
sampling step while gradually guiding the swarm
from a global to more local exploration:
w(c) =
A
e
c
, c ∈ [0, ln(10A)], (2)
where A denotes the starting value of w when the sam-
pling variable c = 0 and c is incremented by ∆c =
ln(10A)/C, where C is the desired number of inertia
weight changes. The optimisation terminates when
w(c) falls below 0.1.
4 BODY MODEL AND COST
FUNCTION
In this section, we present a short summary of the
body model and the cost function proposed by (Balan
et al., 2005), which we adopt in our implementation.
We adopt this framework to ensure a fair comparison
with other body tracking algorithms reported.
4.1 Body Model
The human body shape is modelled as a collection of
truncated cones (Figure 1(a)). The underlying artic-
ulated motion is modelled with a kinematic tree con-
taining 13 nodes, each node corresponding to a spe-
cific body joint. For illustration, the indexed joints
are shown overlaid on the test subject in Figure 1(b).
Every node can have up to 3 rotational DOF, while
the root node also has 3 translational DOF. In total,
we use 31 parameters to describe the full body pose
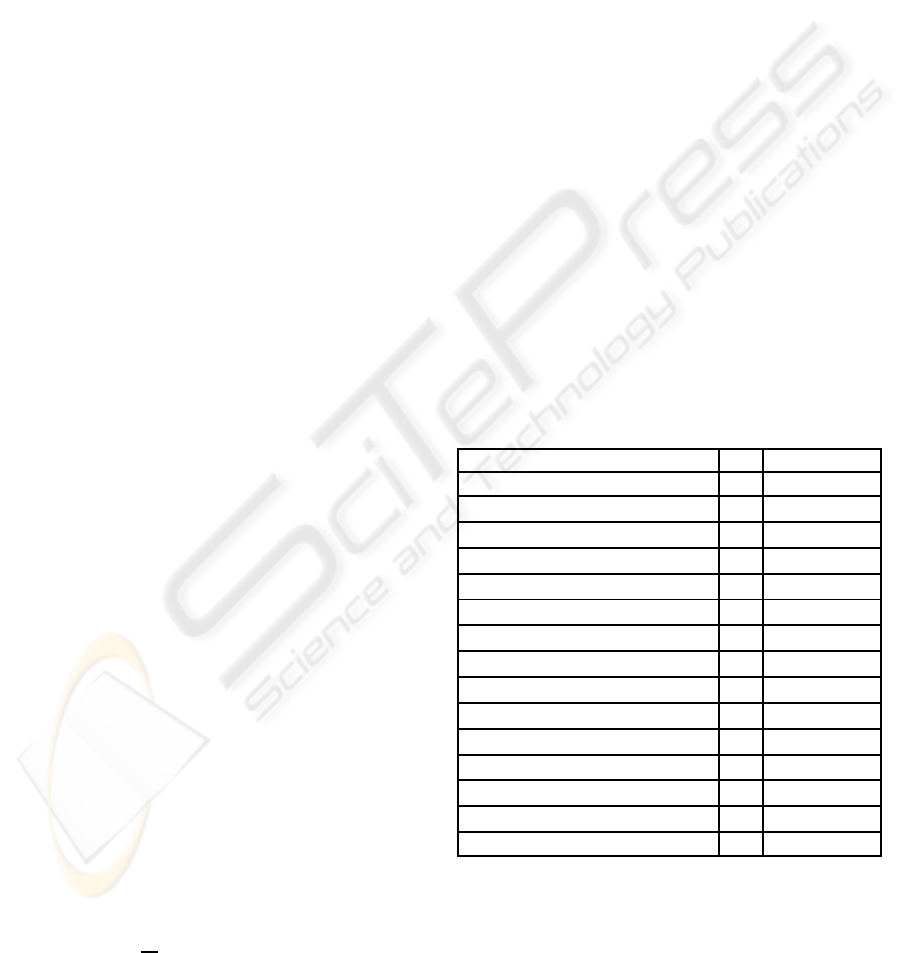
(Table 1).
Table 1: Joints and their DOF.
JOINT (index) # DOF
Global body position (1) 3 r
x
,r
y
,r
z
Global body orientation (1) 3 α
1
x
,β
1
y
,γ
1
z
Torso orientation (2) 2 β
2
y
,γ
2
z
Left clavicle orientation (3) 2 α
3
x
,β
3
y
Left shoulder orientation (4) 3 α
4
x
,β
4
y
,γ
4
z
Left elbow orientation (5) 1 β
5
y
Right clavicle orientation (6) 2 α
6
x
,β
6
y
Right shoulder orientation (7) 3 α
7
x
,β
7
y
,γ
7
z
Right elbow orientation (8) 1 β
8
y
Head orientation (9) 3 α
9
x
,β
9
y
,γ
9
z
Left hip orientation (10) 3 α
10
x
,β
10
y
,γ
10
z
Left knee orientation (11) 1 β
11
y
Right hip orientation (12) 3 α
12
x
,β
12
y
,γ
12
z
Right knee orientation (13) 1 β
13
y
TOTAL 31
4.2 Cost Function
The cost function measures how well a candidate
body pose matches the pose of the person in the video
sequence. It consists of two parts, an edge-based part
and a silhouette-based part.
ARTICULATED HUMAN MOTION TRACKING WITH HPSO
533

In the edge-based part, a binary edge map is ob-
tained by thresholding the image gradients. This map
is then convolved with a Gaussian kernel to create a
edge distance map, which determines the proximity of
a pixel to an edge. The model points along the edge of
the truncated cones are projected onto the edge map
and the mean square error (MSE) between the pro-
jected points and the edges in the map is computed.
In the silhouette-based part, a silhouette is ob-
tained from the input images by statistical background
subtraction with a Gaussian mixture model. A prede-
fined number of points on the surface of the 3-D body
model is then projected into the silhouette image and
the MSE between the projected points and the silhou-
ette computed.
Finally, the MSEs of the edge-based part and
silhouette-based part are combined to give the cost
function value f(x
i
) of the i-th particle :
f(x
i
) = MSE
i
edge
+ MSE
i
silhouette
(3)
(a) (b) (c)
Figure 1: (a) The truncated-cone body model. (b) Joint po-
sitions. (c) Kinematic tree.
5 HPSO ALGORITHM
The work presented in this paper is an extension of
(Ivekovic and Trucco, 2006; Ivekovic et al., 2008)
where a PSO-based hierarchical framework is used to
estimate the articulated upper-body pose with multi-
view still images. This work extends the approach
to tracking the full-body pose in multi-view video
sequences. The tracking algorithm consists of three
main components: the initialisation, the hierarchi-
cal pose estimation and the next-frame propagation,
which we describe next.
5.1 Initialisation
The initialisation is fully automatic. Each particle in
the swarm is assigned a random 31-dimensional po-
sition in the search space. A particle’s position rep-
resents a possible body pose configuration, with the
position vector specified as:
x
i
= (r
x
,r
y
,r
z
,α
1
x
,β
1
y
,γ
1
z
,...,α
K
x
,β
K
y
,γ
K
z
), (4)
where r
x
,r
y
,r
z
denote the position of the entire body
(root of the kinematic tree) in the world coordinate
system, and α
k
x
,β
k
y
,γ
k
z
, k = 1...K, refer to rotational
degrees of freedom of joint k around the x, y, and z-
axis, respectively, where K +1 is the total number of
joints in the kinematic tree. Each particle is also as-
signed a random 31-dimensional velocity vector, giv-
ing it an exploratory direction in the search space.
5.2 Hierarchial Pose Estimation
PSO has been successfully applied to various non-
linear optimisation problems (Poli, 2007; Poli et al.,
2008). However, as pointed out by (Robertson and
Trucco, 2006; Ivekovic and Trucco, 2006), it becomes
computationally prohibitive with increasing numbers
of optimised DOF.
In order to make the implementation computation-
ally feasible, we solve the pose estimation in a hierar-
chical manner, where the kinematic tree modelling the
articulated motion is estimated in several stages, start-
ing at the root and proceeding downwards towards the
leaves. This is possible because the kinematic struc-
ture of the human body contains an inherent hierar-
chy in which the joints lower down the kinematic tree
(e.g., elbows) are constrained by the joints higher up
the tree (e.g., shoulders).
We use this property to subdivide the search space
into several subspaces containing only a subset of
DOF each, thus reducing the search complexity. The
hierarchy of the kinematic structure starts with the po-
sition and orientation of the entire body in the world
coordinate system. Changing either of these affects
the configuration of every joint in the model. The
kinematic tree then branches out into 5 chains: one
for the neck and head, two for left and right arm, and
two for left and right leg. The chains modelling the
upper body form a subtree with the torso orientation
as the root node. From the root node they then branch
out independently.
The 5 branches of the kinematic tree are shown
overlaid on the test subject in Figure 1(c). We split
the search space into 12 different subspaces and cor-
respondingly perform the hierarchical optimisation in
12 steps, detailed in Table 2. The subspaces are cho-
sen so that only one limb segment at a time is opti-
mised.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
534

Table 2: Hierarchy of optimisation.
(Step 1) Global body pos.: (Step 5) Left lower arm orient.: (Step 9) Left upper leg orient.:
3DOF: r
x
,r
y
,r
z
2DOF: γ
4
z
,β
5
y
2DOF: α
10
x
,β
10
y
(Step 2) Global body orient.: (Step 6) Right upper arm orient.: (Step 10) Left lower leg orient.:
3DOF: α
1
x
,β
1
y
,γ
1
z
4DOF: α
6
x
,β
6
y
,α
7
x
,β
7
y
2DOF: γ
10
z
,β
11
y
(Step 3) Torso orient.: (Step 7) Right lower arm orient.: (Step 11) Right upper leg orient.:
2DOF: β
2
y
,γ
2
z
2DOF: γ
7
z
,β
8
y
2DOF: α
12
x
,β
12
y
(Step 4) Left upper arm orient.: (Step 8) Head orient.: (Step 12) Right lower leg orient.:
4DOF: α
3
x
,β
3
y
,α
4
x
,β
4
y
3DOF: α
9
x
,β
9
y
,γ
9
z
2DOF: γ
12
z
,β
13
y
5.3 Next-frame Propagation
Once the pose in a particular frame has been esti-
mated, the particle swarm for the next frame is ini-
tialised by sampling the individual particle positions
from a Gaussian distribution centred on the position
of the best particle from the previous frame, with the
covariance set to a low value, in our case 0.01, to pro-
mote temporal consistency.
6 EXPERIMENTAL RESULTS
(Balan et al., 2005) published a Matlab implemen-
tation of an articulated full-body tracking evaluation
software, which includes an implementation of PF
and APF. This provided us with a platform to quan-
titatively evaluate our tracking algorithm. We imple-
mented our tracking approach within their framework
by substituting the particle filter code with our HPSO
algorithm. All other parts of their implementation
were kept the same to ensure a fair comparison.
Datasets. In our experiments, we used 4 datasets:
the Lee walk sequence included in the Brown Univer-
sity evaluation software and 3 datasets courtesy of the
University of Surrey: Jon walk, Tony kick and Tony
punch sequences. The Lee walk dataset was captured
with 4 synchronised grayscale cameras with resolu-
tion 640 × 480 at 60 fps and came with the ground
truth articulated motion data acquired by a Vicon sys-
tem, allowing for a quantitative comparison of the
tracking results. The Surrey sequences were acquired
by 10 synchronised colour cameras with resolution
720× 576 at 25 fps.
HPSO Setup. HPSO was run with only 10 particles
and without any hard prior. The PSO parameters (in-
ertia weight model, stopping condition) and the co-
variance of the Gaussian distribution used for prop-
agating the swarm into the next frame were kept the
same across all the datasets to demonstrate the versa-
tility of our algorithm. The starting inertia weight was
kept at 2 and the stopping inertia was fixed at 0.1 for
all the sequences and this amounted to 60 PSO itera-
tions per step in the hierarchical optimisation or 7200
likelihood evaluations per frame (12 steps per frame).
PF/APF Setup. (Balan et al., 2005) use a zero-
velocity motion model, where the noise drawn from a
Gaussian distribution is equal to the maximum inter-
frame difference and different for each dataset. Un-
like the original APF algorithm (Deutscher and Reid,
2005), the Brown software uses a motion-capture-
trained hard prior for the Lee walk sequence to ini-
tialise the tracking and eliminate particles with im-
plausible poses. This significantly improves the ac-
curacy of the APF tracking algorithm as seen in
(Balan et al., 2005) and also confirmed by our exper-
iments. Since we wanted to compare our algorithm
with the original APF algorithm by (Deutscher and
Reid, 2005), we ran our tests without the hard prior,
except for initialisation which otherwise failed, as de-
scribed later.
Testbed Choice. To select the appropriate compari-
son testbed for PF, APF and HPSO, we ran two tests.
In the first one, all three algorithms were set up to use
the same number of likelihood evaluations to find the
solution. In the second one, all three were given the
same computation time. The setup was normalised
to HPSO which required 7200 evaluations and took
70 seconds per frame. We therefore ran the PF with
7200 particles and the APF with 1440 particles and
5 annealing layers in the first experiment (Setup A),
and PF with 3000 particles and APF with 600 parti-
cles and 5 annealing layers in the second experiment
(Setup B). The results of the first experiment showed
Table 3: MAP error in mm for the LeeWalk sequence with
varying number of likelihood evaluations.
Algorithm testbed MAP error
PF (Setup A) 70.0± 21.2
APF (Setup A) 68.38± 17.5
PF (Setup B) 72± 20.5
APF (Setup B) 68.83± 25
HPSO (Setup A,B) 46.5±8.48mm
ARTICULATED HUMAN MOTION TRACKING WITH HPSO
535

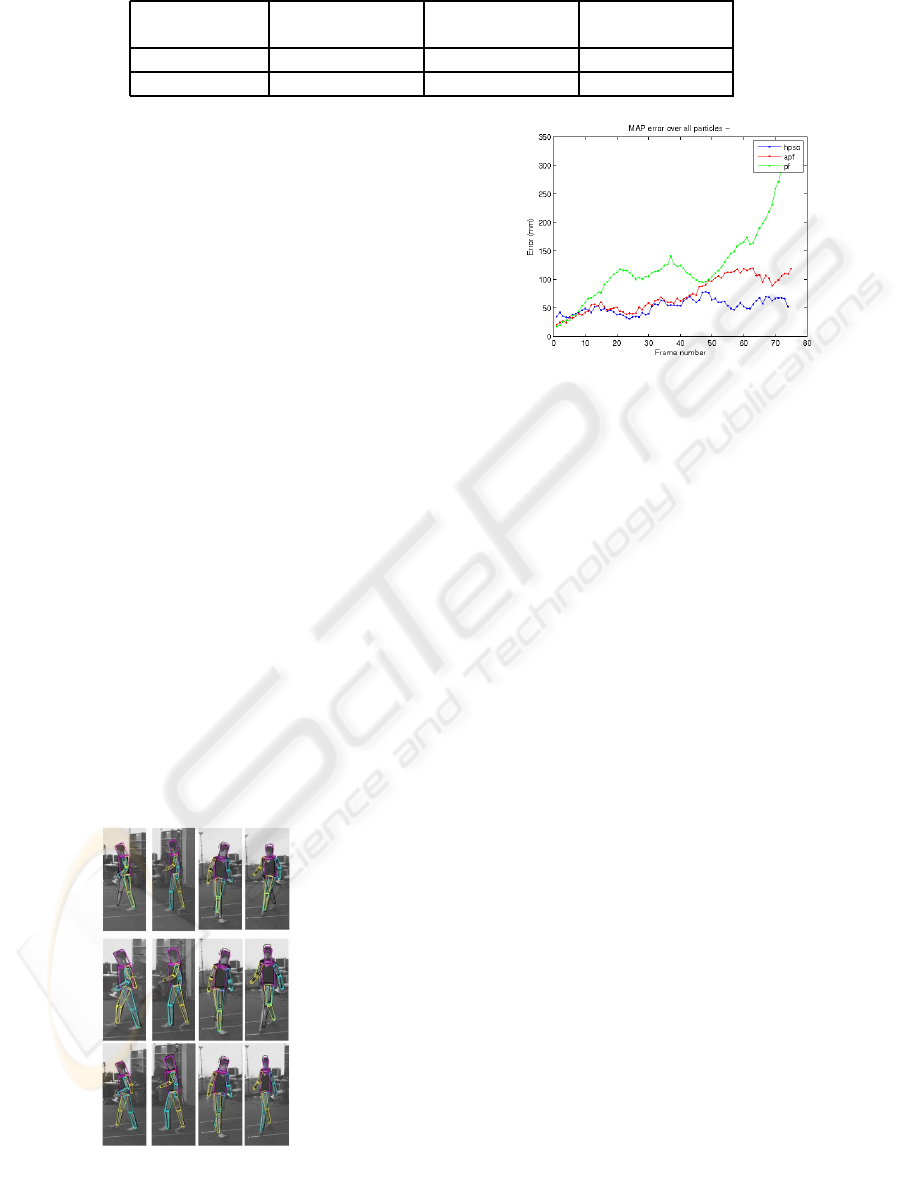
Table 4: The distance error calculated for the Lee Walk sequences.
Sequence PF APF HPSO
Mean ± Std.dev Mean ± Std.dev Mean ± Std.dev
LeeWalk60Hz 72± 20.55mm 68.38 ± 25mm 46.5± 8.48mm
Leewalk30Hz 125.5± 56.7mm 72.6±29.9mm 52.5±11.7mm
that the same number of likelihood evaluations in-
creased the temporal complexity of APF and PF to
thrice that of PSO. Our results (Table 3), show that the
tracking accuracy does not increase significantly with
the increased number of particles. This result is paral-
lel to the results observed in (Husz et al., 2007), where
increasing the particle numbers beyond 500 does not
result in any additional improvement. When compar-
ing on the basis of temporal complexity, HPSO also
outperformed both PF and APF (Table 3). Due to the
high temporal complexity of PF and APF associated
with Setup A, we decided to perform the rest of the
experiments based on the Setup B.
Lee Walk Results. The results obtained at 60 fps
(Figure 2) show that the performance of HPSO is
comparable to that of APF and better than that of
PF. Table 4 shows the error calculated as the distance
between the ground-truth joint values and the values
from the pose estimated in each frame, averaged over
5 trials. We also performed a comparison with a tem-
porally subsampled Lee walk sequence by downsam-
pling to 30 fps to increase the inter-frame motion.
The distance error tabulated in Table 4 shows that the
HPSO performs better than both the APF and the PF
at the reduced frame rate. The graph comparing the
distance-error for 30 fps sequences is shown in Fig-
ure 3. Results show that the accuracy of HPSO is not
significantly affected by faster motion, while the per-
formance of the APF and PF deteriorates.
Figure 2: The results for the 60 fps Lee walk sequence for
frames 1, 40, 80 and 120 with PF, APF and HPSO results in
the 1st, 2nd and 3rd row, respectively.
Figure 3: The distance error graph for 30 fps.
Surrey Sequence Results. The Surrey test sequences
contained faster motion than the Lee walk sequence.
For rapid and sudden motion in the punch and kick
sequence, HPSO performed better than APF and PF
(Figure 7,6). Since we do not have the ground truth
data for the Surrey dataset, we could not compute
numerical errors as in the case of the Lee walk se-
quence. Instead, we chose to measure the overlap of
the model’s silhouette in the estimated pose with the
image silhouettes and edges by modifying our cost
function. The estimated pose measure O
n
for the n-th
frame is given as:
O
n
= OvrLap
n
edge
+ OvrLap
n
silhouette
(5)
The average overlap and standard deviation for a
given sequence over 5 trials are shown in Table 5.
Recovery. Our experiments also confirmed that
HPSO has the ability to recover from a wrong es-
timate, unlike PF and APF, where the error after a
wrong estimate normally increases (the problem of
divergence). E.g., in Figure 5, the right elbow is
wrongly estimated by APF and is never recovered.
This behaviour is even more pronounced in the PF.
HPSO, on the other hand, recovers and finds the
correct estimate in the following frame, in spite of
wrongly estimating it in the previous frame (Figure
5).
Automatic Initialisation. HPSO can initialise auto-
matically on the first frame of the sequence. We tested
the automatic initialisation on all 4 test sequences. A
canonical initial pose (Figure 4(a,e)) was given as a
starting point. The HPSO algorithm, initialised by
sampling from a random distribution centered at the
canonical pose, consistently found the correct posi-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
536

Table 5: The silhouette/edge overlap measure for the Surrey sequence. Bigger number means better performance.
Sequence PF APF HPSO
Mean ± Std.dev Mean ± Std.dev Mean ± Std.dev
Jon Walk 1.311±0.027 1.350±0.025 1.3853±0.015
Tony Kick 1.108±0.095 1.197±0.041 1.2968±0.024
Tony Punch 1.253±0.018 1.26±0.01 1.3296±0.0117
(a) (b) (c) (d) (e) (f) (g) (h)
Figure 4: The automatic initialisation results for the Lee walk (left) and Tony Kick (right) sequence. (a,e) The canonical
initial pose for all three algorithms. (b,f) Unsuccessful PF and (c,g) unsuccessful APF initialisation. (d,h) successful HPSO
initialisation.
tion and orientation of the person in the initial frame,
while PF and APF failed to find a better estimate due
to the given starting point being too far from the solu-
tion.
(a) Frame 28 (b) Frame 29
Figure 5: (a) an incorrect HPSO estimate due to error prop-
agation (b) the estimate is corrected in the next frame.
7 CONCLUSIONS AND FUTURE
WORK
We presented a hierarchical PSO algorithm (HPSO)
for full-body articulated tracking, and demonstrated
that it performs better than APF and PF, most notably
in sequences with fast and sudden motion. HPSO
also successfully addresses the problem of particle fil-
ter divergence through its search strategy and parti-
cle interaction and reduces drastically the need for a
sequence-specific motion model.
An inherent limitation of algorithms with a weak
motion model, is the dependence of its accuracy on
the observation. In case of noisy silhouettes or miss-
ing body parts the accuracy would decrease. Another
Figure 6: Results of Tony kick sequence illustrated for
frames 1, 15 and 25. The PF, APF and HPSO results are
displayed in the first, second and third row respectively.
limitation that became evident during the experimen-
tal work, was error propagation: due to the hierarchi-
cal and sequential structure of the HPSO algorithm,
an incorrect estimate higher up in the kinematic chain
infuenced the accuracy of all the subsequent hierar-
chical steps. Although undesired, the error propaga-
tion was not fatal for the performance of the HPSO
tracker, as it was still able to recover from a bad esti-
mate in the subsequent frames (Figure 5).In our future
ARTICULATED HUMAN MOTION TRACKING WITH HPSO
537

Figure 7: Results of Tony punch sequence, illustrated for
frames 1, 15 and 25. The PF, APF and HPSO results are
displayed in the first, second and third row respectively.
work, we will address the error propagation problem
as well as incorporate a better next frame strategy to
further increase the accuracy and decrease the time
complexity of the search.
ACKNOWLEDGEMENTS
This work is supported by EPSRC grant EP/080053/1
Vision-Based Animation of People in collaboration
with Prof. Adrian Hilton at the University of Sur-
rey (UK). We refer the readers to (Starck and Hilton,
2007) for further information on the Surrey test se-
quences.
REFERENCES
Balan, A. O., Sigal, L., and Black, M. J. (2005). A quan-
titative evaluation of video-based 3d person tracking.
In ICCCN ’05: Proceedings of the 14th International
Conference on Computer Communications and Net-
works, pages 349–356. IEEE Computer Society.
Caillette, F., Galata, A., and Howard, T. (2008). Real-time
3-d human body tracking using learnt models of be-
haviour. Computer Vision and Image Understanding,
109(2):112–125.
Deutscher, J. and Reid, I. (2005). Articulated body motion
capture by stochastic search. International Journal of
Computer Vision, 61(2):185–205.
Husz, Z., Wallace, A., and Green, P. (2007). Evaluation
of a hierarchical partitioned particle filter with action
primitives. In CVPR 2nd Workshop on Evaluation of
Articulated Human Motion and Pose Estimation.
Isard, M. and Blake, A. (1998). CONDENSATION - con-
ditional density propagation for visual tracking. Inter-
national Journal of Computer Vision, 29(1):5–28.
Ivekovic, S. and Trucco, E. (2006). Human body pose esti-
mation with pso. In Proceedings of IEEE Congress on
Evolutionary Computation (CEC ’06), pages 1256–
1263.
Ivekovic, S., Trucco, E., and Petillot, Y. (2008). Human
body pose estimation with particle swarm optimisa-
tion. Evolutionary Computation, 16(4).
Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-
mization. In Proceedings of the IEEE International
Conference on Neural Networks, volume 4, pages
1942–1948.
MacCormick, J. and Isard, M. (2000). Partitioned sam-
pling, articulated objects, and interface-quality hand
tracking. In Proceedings of the European Conference
on Computer Vision (ECCV’00) - volume 2, number
1843 in Lecture Notes in Computer Science, pages 3–
19, Dublin, Ireland.
Poli, R. (2007). An analysis of publications on particle
swarm optimisation applications. Technical Report
CSM-649, University of Essex, Department of Com-
puter Science.
Poli, R., Kennedy, J., Blackwell, T., and Freitas, A.
(2008). Editorial for particle swarms: The second
decade. Journal of Artificial Evolution and Applica-
tions, 1(1):1–3.
Poppe, R. (2007). Vision-based human motion analysis: An
overview. Computer Vision and Image Understanding
(CVIU), 108(1-2):4–18.
Robertson, C. and Trucco, E. (2006). Human body pos-
ture via hierarchical evolutionary optimization. In In:
BMVC06. III:999.
Robertson, C., Trucco, E., and Ivekovic, S. (2005). Dy-
namic body posture tracking using evolutionary opti-
misation. Electronics Letters, 41:1370–1371.
Shi, Y. H. and Eberhart, R. C. (1998). A modified parti-
cle swarm optimizer. In Proceedings of the IEEE In-
ternational Conference on Evolutionary Computation,
pages 69 – 73.
Sminchisescu, C. and Triggs, B. (2003). Estimating ar-
ticulated human motion with covariance scaled sam-
pling. International Journal of Robotic Research,
22(6):371–392.
Starck, J. and Hilton, A. (2007). Surface capture for per-
formance based animation. IEEE Computer Graphics
and Applications, 27(3):21–31.
Vondrak, M., Sigal, L., and Jenkins, O. C. (2008). Phys-
ical simulation for probabilistic motion tracking. In
Proceedings of CVPR 2008, pages 1–8.
Zhang, X., Hu, W., Maybank, S., Li, X., and Zhu, M.
(2008). Sequential particle swarm optimization for vi-
sual tracking. In Proceedings of CVPR 2008.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
538