BREADER:

A MODULAR FRAMEWORK FOR VISION

RECOGNITION OF MATHEMATICAL-LOGICAL STRUCTURES

Celia Salmim Rafael

ESTM, IPLeiria, Peniche, Portugal

Jorge Simao

DCC-Faculty of Sciences-University of Porto, Center for the Science of Computation

Cognition and Complexity, Porto, Portugal

Keywords:

Pattern Analysis and Recognition, Geometry Visual Recognition, Mathematical Expression Visual Recogni-

tion, Symbol and Structure Recognition.

Abstract:

We describe a system that uses image processing and computer vision techniques to discover and recognize

mathematical, logical, geometric, and other structures and symbols from bit-map images. The system uses

a modular architecture to allow easy incorporation of new kinds of object recognizers. The systems uses

a “blackboard” data-structure to retain the list of objects that have been recognized. Particular object rec-

ognizers check this list to discover new objects. Initially, objects are simple pixel clusters resulting from

image-processing and segmentation operations. First-level object recognizers include symbol/character rec-

ognizers and basic geometric elements. Higher-level object recognizers collect lower-level objects and build

more complex objects. This includes mathematical-logical expressions, and complex geometric elements such

as polylines, graphs, and others. The recognized objects and structures can be exported to a variety of vector

graphic languages and type-setting systems, such as SVG and L

1 INTRODUCTION

We describe a system that uses image processing and

computer vision techniques to discover and recognize

mathematical, logical, geometric, and other structures

and symbols from bit-map images. The system uses

a modular architecture to allow easy incorporation of

new kinds of object recognizers. The system uses a

“blackboard” data-structure to retain the list of ob-

jects that have been recognized. Particular object rec-

ognizers check this list to discover new objects (Nii,

1986). Initially, objects are simple pixel clusters re-

sulting from image-processing and segmentation op-

erations. First-level object recognizers include sym-

bol/character recognizers and basic geometric ele-

ments. Higher-level object recognizers collect lower-

level objects and built more complex objects. This

includes mathematical-logical expressions, and com-

plex geometric elements such as polylines, graphs,

and others.

The recognized objects and structures can be ex-

ported to a variety of vector graphic languages and

type-setting systems, such as SVG and L

X. The

selection of recognition operations performed by the

system can be selectable according to the application

domain (e.g. mathematics, logics, geometry construc-

tion, program code, etc.). The systems also allow in-

teraction with the user, including selection of different

domains and/or recognizers in different regions of the

same image.

Symbol recognition relies on the computation of

simple but highly predictive cues, stored in a data-

base. Experimented cues include spectral (Fourier-

like) feature vector, and other cues related to symme-

try and topology of symbols. A simple classiﬁcation

algorithm, sequential or multi-level nearest-neighbor,

is used to compare extracted features with symbol fea-

ture vectors stored in a data-base.

A graph relating symbols positions and topolog-

ical relations is also built, to allow the construction

of high-order objects coding expressions. The edges

of the topological graph are also stored in the “black-

board” data-structure for simple integration with the

rest of the system. Mathematical-logicals structures

are built by recursive application of composition rules

on object and topological relations.

249

Salmim Rafael C. and Simao J. (2009).

BREADER: A MODULAR FRAMEWORK FOR VISION RECOGNITION OF MATHEMATICAL-LOGICAL STRUCTURES.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 249-255

DOI: 10.5220/0001808702490255

 SciTePress

The recognized object structures can be exported

to a variety of vector graphic languages and type-

setting systems, such as SVG. The recognition and

image processing pipeline is highly conﬁgurable and

can rely on an interactive GUI. This allows parame-

ters to be set and object exporting options to be se-

lected. The system is built in a modular way such that

adding new types of object recognizers or expression

composition rules is simple. We have been evaluating

the system by testing a variety of images, such as spe-

cially prepared images, and photography images from

classroom boards. The system current version is im-

plementation in R, with plan to be reimplemented in

JAVA.

2 SYSTEM OVERVIEW

The goal of our system is to map raster-images (bit-

maps in some format), containing semantic informa-

tion in mathematical, geometrical, or diagramatic no-

tations, to a vector graphics or other symbolic repre-

sentations. For example, a bit-map image with a line

and a circle, should be mapped to a vector graphics

representation that includes a parametric object rep-

resenting the line, and another parametric object rep-

resenting the circle. Likewise, symbols should be rep-

resented as text like representation (as in OCR), and

mathematical formulas should have a compact rep-

resentation (e.g. expression tree). To make the sys-

tem open, we want the vector representation to be ex-

ported to a variety of formats. Moreover, we want the

system to be modular to allow easy incorporation of

new kinds of object recognizers as the system is de-

veloped and new domains are focused.

The system uses a ‘blackboard” data-structure and

architecture where a list of objects, designated hereby

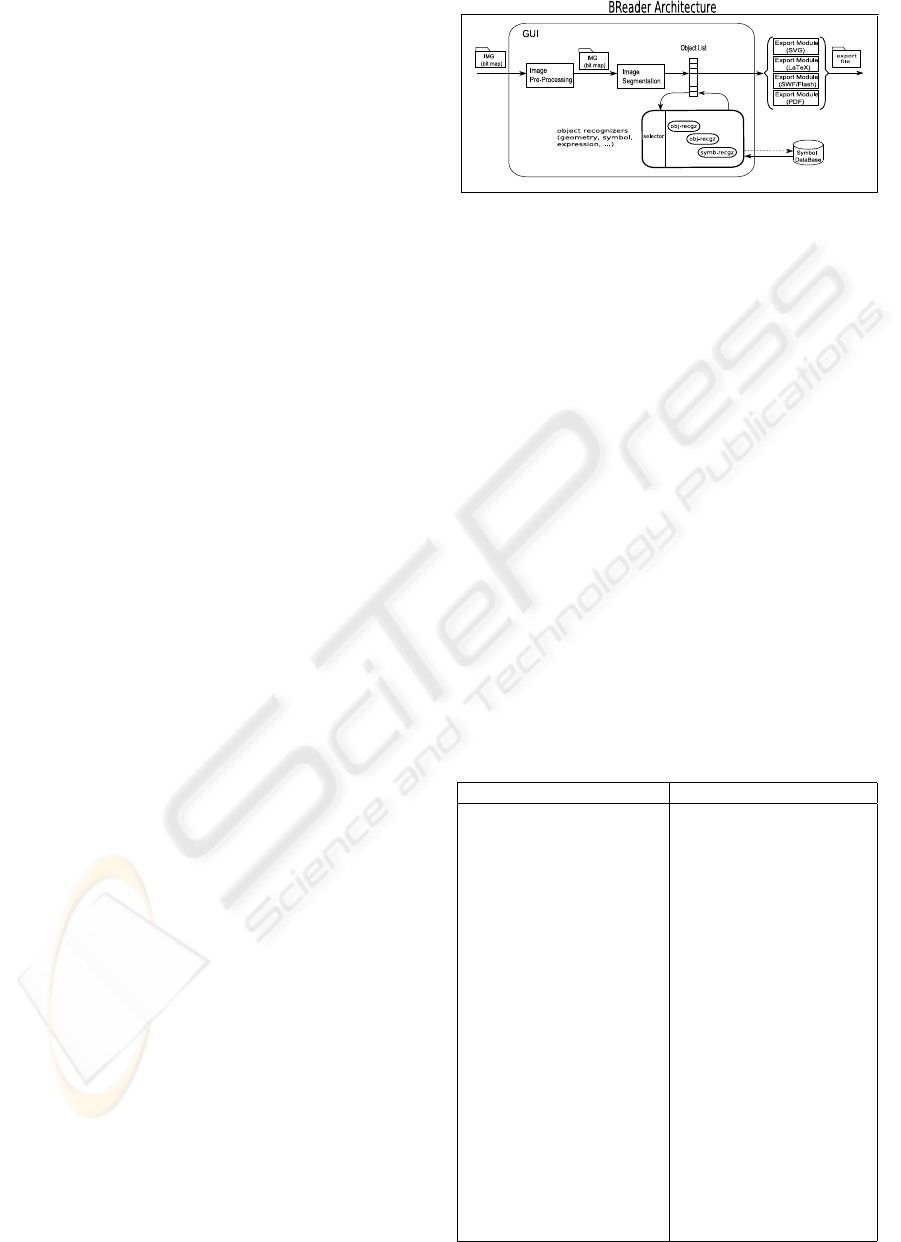
lob j, contains all recognized objects so far. Fig-

ure 1 presents a diagrammatic representation of the

proposed system architecture. Initially, raster-images

are fed as input to an image pre-processing module

that prepares the images to further processing. Ad-

ditionally, an image segmentation operation is used

to identify level-0 objects, consisting of pixel clus-

ters, deﬁned as connect or semi-connect line paths

or point sets. This is stored as cluster(lpx) object,

where argument l px is the list of pixel in the clus-

ter. Thus, at an early stage of recognition we have

lob j = {cluster(l px

)}.

A set of higher-order object recognizers is then

used to build more complex objects. Some recog-

nizers deal with geometric structures, other deal with

symbol recognition and mathematical-logical expres-

sions building. An intermediate step is to identify

Figure 1: BREADER Architecture as a block diagram.

topological and spatial relations between symbol that

can be used by expression building operations. All

these object recognizers produce as output further

parametrized objects, that are inserted in the object

list lob j. The components objects of a more com-

plex object are usually removed from the list of object

to prevent multiple solution to the recognition pro-

cess. For example, if a circle is recognized in a pixel

cluster and object cluster(l px) is replaced by an ob-

ject circle(c, r). Like-wise, if two clusters are recog-

nized as symbol objects, then objects sym(text

) and

sym(text

) are introduced in the list of object. Further

processing may recognize the two symbol as part of

a (sub-)expression, and are replaced by an object of

the type expr(op,text

,text

), where op is the type of

operation.

The ﬁnal list of objects can be exported to a vari-

ety of ﬁle formats for vector graphics and/or typeset-

ting systems. Below, we summarize the list of object

current version of BREADER supports:

Table 1: Summary of objects recognized by the system.

object purpose

bit-map objects

cluster(l px) set of (semi-)connected pixels

resulting from segmentation

simple geometry object

line(x

, y

, x

, y

) line-segment connecting

point (x

, y

) and (x

, y

)

circle(c

, c

, r) circle with center at (c

, x

)

and radius r

second-level geometry object

polyline() connected line-segments

symbols

cues(cm, bb, f s

, f s

, . . .) list of cues: f s

, center-of-mass,

bounding box

sym(label,cm, bb) symbol object after classiﬁcation

topological and spatial relations

rel(type, sym

d, sym

d) object type for each

identiﬁed relation

expression

expr(op, sym

, sym

, ...) object type expression:

op is the type of operation

grouping

group(sym

, sym

, ...) object type group

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

250

3 IMAGE SEGMENTATION

The system segments the image by identifying clus-

ters of connected pixels with similar color codes. This

is done by considering the image map as a graph such

that a pixel (x, y) with a color-code different from 1

was a node (vertex) in the graph. Topological neigh-

boring pixels in any of the 8 von Neaumann directions

(N,NE,E,SE,S,SW,W) are assumed to deﬁne a graph

edge if the color code difference is smaller than a pa-

rameter θ

To identify seed or initial pixels for a cluster the

image is scanned left-to-right, top-to-bottom until a

pixel (x, y) is found such that img(x, y) 6= 1. Once a

seed pixel is found a graph search deep-ﬁrst (recur-

sive) algorithm is used to identify the set of pixels that

are directly or indirectly connected to the seed pixel

(a path exist between the two pixels). Repeated pixels

are detected to prevent inﬁnite recursion. As pixels

found are grouped in a list of point C

deﬁning a clus-

ter. A reference color code c(C

) is stored with each

cluster for later selection of colors in vector graphics

ﬁles .

Once a cluster is built it is stored in a global list

of clusters C

∗

≡C

∗

, and scanning resumes one point

further to the left or down in relation to the seed pixel

from last cluster. During scanning, pixels that have

been already included in any cluster, are not consid-

ered as seeds for further clusters.

We perform a variety of pre-processing operation

at the cluster level, that further simplify and enhance

the recognition process. Namely, we remove from the

cluster list all clusters C

with a number of pixel lower

than a ﬁxed threshold θ

. This helps in dealing with

noise and impressions in image processing and/or the

segmentation process. We also smooth clusters using

some window size W , such that each point p

in a clus-

ter is replaced by the mean point of a set of W points

around p

. A point p

is considered to be around

if its index in the cluster list is not further away

than W of the index of p

and the distance ||p

− p

is lower than a threshold θ

. After all segmentation

operations are performed, each identiﬁed cluster pro-

duces a cluster(l px) object that is included in the list

of object lob j.

4 RECOGNITION ALGORITHMS

FOR GEOMETRY

Since the proposed architecture is open-ended new

object recognizers can be introduced at any time. Be-

low, we describe some of algorithms used to recog-

nize simple geometries.

4.1 Sequences Straight Lines

For every segmented cluster, we inspect tangent vec-

tors to see if they have approximately the same ori-

entation. Sequences of tangent vectors considered to

have the same orientation deﬁne a straight line/seg-

ment. We deﬁne two tangent vectors to be have ap-

proximately the same orientation if the dot-product is

not below some threshold. Every maximal sequence

of vectors with the same orientation (larger than 2)

is replaced by a line(.) object. One particular clus-

ter may produce several line(.), that may be further

processed.

4.2 Polylines and Circles

Given a list of line objects line(.) obtained from a

cluster processing, as described above, we can addi-

tionally see what line segments are close enough by

to form a polyline. This is useful because many vec-

tor graphics languages and typesetting system have

explicit primitives to deal with polylines. Thus if

one is able to recognize and produce such kind of

object, we can make the exported vector represen-

tation of the image smaller in bytes or characters.

To create a polyline object we check for line objects

that whose end-points are close enough to be consid-

ered connected. This operation is done iteratively as

long as new line(.) objects can be added to the poly-

line. The complete processing of a list of line(.) ob-

jects will in general generate a list of polyline(.) ob-

jects and a remaining list of line(.) not included in

any polyline. In general, polyline objects will be of

the form polyline(p

, p

, . . . , p

), where p

here is

some end-point of a line object.

To check if a cluster can be recognized as a cir-

cle, we compute the center-of-mass of the set of

points in the cluster, deﬁned as: cm = E[(x

, y

)] =

|C|

∑

i∈[1,|C|]

, y

), where (x

, y

) are points in cluster

C. We then compute the mean distance (radius) of all

point to the center-of-mass. The test to see if a cluster

represents a circle is done by seeting an upper-bound

for the mean deviation to the center-of-mass. A circle

object is created with cm and ¯r as attributes.

5 RECOGNITION OF SYMBOLS

AND EXPRESSIONS

Symbol and expression recognition is done at three

levels. First, individual cluster are categorized as par-

ticular symbols. Then topological or spatial relation

between symbol are discovered. Finally, hierarchical

BREADER: A MODULAR FRAMEWORK FOR VISION RECOGNITION OF MATHEMATICAL-LOGICAL

STRUCTURES

251

construction of expressions is done by applying sub-

expression recognizers.

5.1 Cues for Symbols Classiﬁcation

The system takes Fourier-like spectral components

representation for clusters (or line paths), we use sim-

ilar statistics as in recognizing circles. Given a cluster

C ≡ C

we compute the center-of-mass cm, and the

mean-radius ¯r ≡r

. r

is considered the magnitude of

the ﬁrst spectral component. We then generate a de-

rived cluster C

that includes a point for every point

in the original cluster, and made to be at distance σ

of the origin (0, 0) with σ

= r

−¯r, and oriented along

the unitary vector

)

. The second spectral compo-

nent is the mean radius of C

. Likewise, for additional

spectral components. To make spectral cues invari-

ant with symbol size, in addition to symbol rotation,

translation, and reﬂection, we normalize components

by according to ﬁrst component. This produces a cue

vector of the form: [

, . . . ,

Because spectral features might not be enough to

clearly distinguish and correctly classify some sym-

bols, such as reﬂected symbol pair (e.g. ’p’ and ’q’,

’d’ and ’b’, ’∧’ and ’∨’, ’<’ and ’>’), addition fea-

tures are extracted and maintained in database for ev-

ery symbol. This includes mostly features to identify

the asymmetry proﬁle of symbols.

Cues taken for a cluster are stored

in sets, and stored as a objects of type

cues(cm, bbox, f s

, f s

, . . .), where f s

is a vec-

tor with some set of cues. cm is the center-of-mass

of the cluster, and bbox

= [x

min

, y

min

, x

max

, y

max

] is

the bounding box of the cluster. This information is

used to infer topological and spatial relation between

symbols. Once a classiﬁcation operation is performed

a cues(.) object is transformed in a symbol object

of the form symbol(label, cm, bbox), where label is

same label assigned to the segmented cluster.

5.2 Symbol Classiﬁcation and Symbol

Relations

The system can in principle be used with a variety of

classiﬁcation algorithms. So far, we have experiments

with variation of k −nearest −neighboor algorithm

applied to each individual set of cues, and/or combin-

ing multiple sets of cues. In interactive mode assisted

by a GUI, whenever the user does not agree with the

symbol classiﬁcation, it is possible to introduce a new

text-string label l

that is added to symbol data-base.

In order to build expression object to code

mathematical-logical formulas, the system ﬁrst dis-

Graph for x

: Graph for

√

?>=<89:;

(NE,1)

(SE,1)

?>=<89:;

(SW,1)

?>=<89:;

(NW,1)

GFED@ABC

√

(contains)

?>=<89:;

(SW,1)

(NE,1)

²²

?>=<89:;

Figure 2: Topological and spatial relations between sym-

bols in expressions.

covers topological and spatial relation between sym-

bols. This includes directional relations, such as to

“north-west at a certain distance”, positional rela-

tions such as “above-below”, and containment rela-

tions such as “contains-inside”. For each identiﬁed

relation an object of the type rel(type, sym

, sym

) is

stored in the list of object lob j. type codes the type of

relation, and sym

, sym

and are indexes to the symbol

in the relation.

Figure 2 illustrates the identiﬁed relation for two

simple mathematical expressions.

5.3 Symbol Expressions

To build symbol expression graphs, a set of ex-

pression recognizers is used to incrementally build

expressions and expression components. Each

expression recognizer codes a particular kind of

sub-expression. Currently, we have deﬁned

and implemented recongizers for the following

sub-expressions: superscript and subscript rela-

tions, roots, fractions, and operator-operands sub-

expression.

In order to build expression object to code

mathematical-logical formulas, the system ﬁrst dis-

covers topological and spatial relation between sym-

bols. This includes directional relations, such as to

“north-west at a certain distance”, positional rela-

tions such as “above-below”, and containment rela-

tions such as “contains-inside”. For each identiﬁed

relation an object of the type rel(type, sym

, sym

) is

stored in the list of object lob j. type codes the type of

relation, and sym

, sym

and are indexes to the symbol

in the relation.

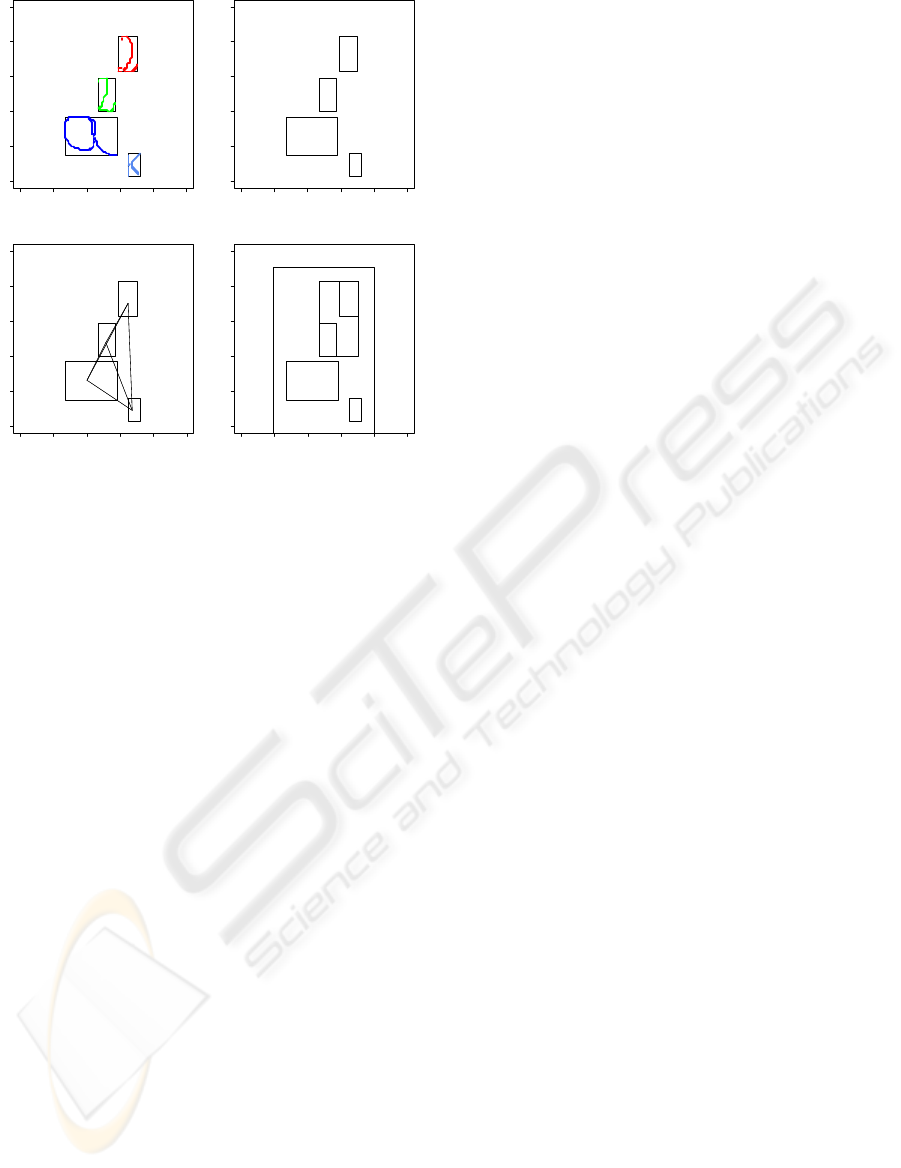
Figure 3 illustrates a complete process to build a

symbol expression graph including the segmentation

process and a topological and expression graph.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

252

0 20 40 60 80 100

cl1 (0)

cl2 (1)

cl3 (2)

cl4 (3)

0 20 40 60 80 100

2 (4)

2 (5)

a (6)

k (7)

0 20 40 60 80 100

2 (4)

2 (5)

a (6)

k (7)

0 20 40 60 80 100

super/subscript (28)

a (6)

k (7)

superscript (33)

2 (5)

2 (4)

Figure 3: Complete process to build symbol expression

graph - segmentation, topological and expression graph.

6 DEALING WITH OBJECT

INTERCEPTIONS

Dealing with object interception, we allow object rec-

ognizers to “consume” only part of the set of pixels

in a cluster. Remaining pixel cluster are reinserted in

the list of objects, as object of type cluster(.), to be,

possibly, further processed by additional object recog-

nizers. For example, a cluster representing the inter-

ception of a circle and line, may be ﬁrst recognized as

a straight line, and the remaining pixel afterwards rec-

ognized as a circle. The robustness of the used mech-

anism to different types of interceptions and objects

is still subject for further investigations.

7 GROUPING OBJECTS

Since vector graphics and typessting systems often al-

low objects to be grouped (e.g. with combined trans-

formation, such as translation and scaling), the pro-

posed system also allow object grouping. This is done

interactively by combined selection via GUI, or us-

ing a close-by heuristic. Namely, objects with pixels

at a distance lower than a threshold θ

are grouped

together. Naturally, this may generate groups that

have objects further apart due to inclusion by asso-

ciativity (e.g., if we have a is −close b and b is −

close c, then by associativity a, b, c are included in

the same group. Relative positioning of individual

object is maintained in the object group. A group is

instantiated in the list of objects as an object of type

group(ob j

, . . . , ob j

), that can later be exported to

some ﬁle format.

8 EXPORTING TO VECTOR

GRAPHICS FORMATS

The presented system implementation allowed to ex-

port the list of recognized objects (geometry and sym-

bols) to several vector graphics languages and type-

setting systems. This is done simply by iterating over

the list of objects, and creating an equivalent object

in the target system or language for every found ob-

ject. In cases, where there is no direct conversion the

output may approximate the objects in some form.

SVG is a W3 standard for vector graphic repre-

sentations based on a XML syntax and technology.

Basic geometric objects, such as lines, polylines, and

circles, can be converted directly to SVG. Recog-

nized text symbols are mapped to SVG text objects.

We are investigating a way to approach the presenta-

tion in SVG of mathematical symbols not covered by

ASCII code and also Greek letters. We are working

to extend the system to export recognized geometries

and symbolic expressions to other vector languages

and/or type-setting systems. In particular, we plan to

export math formulas to TEX/L

Xand geometries to

one or several of its packages (such as ﬁg, pstricks,

and xypic). SWF/Flash and direct PDF conversion

are also planned.

9 IMPLEMENTATION AND

INTERACTION

We have implemented a prototype version of the sys-

tem in the R statistics language and RTE for a fast

prototype and to test the robustness of the algorithms.

R RTE is slow, and it is hard to work as practical

system for complex images. GUI interaction mech-

anisms are also limited in R. We are currently work-

ing in a JAVA version, for higher performance, web

access, and elaborated interaction.

Since it is hard to deﬁne a common set of parame-

ters or order of application of recognizers to all im-

ages, GUI interaction is useful to deﬁne parameter

setting on a per-image basis. Moreover, in complex

images the best setting may depend on regions of the

image. To support this kind of detailed interaction, a

GUI has been developed to allow the user to set pa-

rameters and enable recognizers for speciﬁc regions.

BREADER: A MODULAR FRAMEWORK FOR VISION RECOGNITION OF MATHEMATICAL-LOGICAL

STRUCTURES

253

For example, if the user knows that a region of an

image only contains geometric elements, symbol and

expression recognition may be turn off.

10 RELATED WORK

The accurate recognition of Latin-script, typewritten

text is now considered largely a solved problem. Al-

though certain applications whith higher accuracy re-

quire human review for errors. Handwriting recogni-

tion problem, including recognition of hand printing,

cursive handwriting, is still the subject of active re-

search.

Systems for handwriting recognition are referred to

as off-line or on-line systems(Rjean Plamond, 2000).

Breader focus on off-line handwriting recognition,

since it does not assume a temporal dimension asso-

ciated to the writing action and recognition proccess.

Handwriting character and word recognition is an ap-

proach to symbol recognition and expression recog-

nition. Lee (Lee et al., 2007) describes a trainable,

multi-stroke symbol recognizer that is insensitive to

orientation, non-uniform scaling, and drawing order.

Progress has been reported in the area of dia-

gram recognition, although most projects have been

speciﬁc to a particular domain where recognition is

tailored to the symbols and graphical elements of

a particular type of diagram (Freeman and Plim-

mer, 2007; Chung et al., 2005). In (Kara and Sta-

hovich, 2004) the author present an approach for com-

bined recognition of hand-drawn and diagrammatic

sketches. Graph-based methods have been an been

used for object representation and matching, and have

been applied to hand-drawn pattern recognition prob-

lems (Chan and Yeung, 2000). With these methods,

sketched symbols are ﬁrst decomposed into basic ge-

ometric primitives, such as lines and arcs, which are

then assembled into a graph structure that encodes

both the intrinsic attributes of the primitives and the

geometric relationships between them.

Different approaches have been proposed for sym-

bol recognition, including template matching ap-

proaches and structural approaches. Neuronal net-

work and statistical approaches (C.C. Tappert and

Wakahara, 1990; Mori et al., 1992) and algorithms

based on nearest-neighbor are most used methods for

implementing classiﬁers (Ha et al., 1995; Miller and

Viola, 1998).

Mathematical expressions recognition is a speciﬁc

form of pattern recognition that usually involves two

main stages: symbol recognition and structural anal-

ysis. Symbol recognition involve a sub-step to per-

form image segmentation followed by recognition of

individual text or mathemathical symbols. Structural

analysis is used to reconstruct the hierarchical struc-

ture of mathemathical expression. The survey paper

(Chan and Yeung, 2000), the authors review most of

the existing work on the topic.

Several papers explore speciﬁc problems related

to mathematical notation (Blostein and Grbavec,

1996). In (Miller and Viola, 1998), the author deal

with the particular issue of ambiguities that occur in

mathematical expression recognition. Ming et al.(Li,

2006), presents work to recognize printed mathemat-

ical expressions from document images, based on

method of parsing mathematics notation, which is

based on the combined strategy of baseline and mini-

mum spanning tree method.

A distinguishing feature of the architecure pro-

posed in this article is the focus on modularity, gen-

erality, extensability. Using a blackboard architec-

ture where symbolic representation of recognized ob-

jects can be posted and fetched allows incorporation

of new types of object recognizers. In particular, this

allows geometrical and symbolical structures as found

in mathemathical-logical expression to be recognized

in combination. This is particular useful in complex

diagrams such annotated graphs, many kinds of ﬂow

diagrams, and most diagrams used in mathemathics,

science and engineering lectures.

11 CONCLUSIONS AND FUTURE

WORK

We presented a modular system architecture for com-

bined visual recognition of geometrical, symbolical,

mathematical structures. The system allow new kinds

of object recognizers to be added and selected as

needed. A “blackboard” data-structure is used to re-

tain all recognized object so far, and particular recog-

nizers check this list to discover new objects. Initially,

objects are simple pixel clusters resulting from image-

processing and segmentation operations. First-level

object recognizers include symbol/character recog-

nizers and basic geometric elements. Higher-level ob-

ject recognizers collect lower-level objects and build

more complex objects. This includes mathematical-

logical expressions, and complex geometric elements

such as polylines, graphs, and other. The recognized

objects and structures can be exported to a variety

of vector graphic languages and type-setting systems,

such as SVG and L

X. The systems also allow in-

teraction with the user, including selection of differ-

ent domains and/or recognizers in different regions of

the same image. Future work includes implementa-

tion of additional recognizers, including very high-

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

254

level object such as graph, function plots, and generic

diagrams. Support for recognizers of more complex

mathematical expression such as found in matrix al-

gebra is desired. Mechanisms for coordination of

multiple types of recognizers, possibly independently

developed, is also subject to further investigation.

REFERENCES

Blostein, D. and Grbavec, A. (1996). Recognition of math-

ematical notation.

C.C. Tappert, C. S. and Wakahara, T. (1990). The state

of the art in on-line handwriting recognition. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 12:787–808.

Chan, K.-F. and Yeung, D.-Y. (2000). Mathematical expres-

sion recognition: a survey. IJDAR, 3(1):3–15.

Chung, R., Mirica, P., and Plimmer, B. (2005). Inkkit: a

generic design tool for the tablet pc. In CHINZ ’05:

Proceedings of the 6th ACM SIGCHI New Zealand

chapter’s international conference on Computer-

human interaction, pages 29–30. ACM.

Freeman, I. J. and Plimmer, B. (2007). Connector semantics

for sketched diagram recognition. In AUIC ’07: Pro-

ceedings of the eight Australasian conference on User

interface, pages 71–78. Australian Computer Society,

Inc.

Ha, J., Haralick, R., and Phillips, I. (1995). Understand-

ing mathematical expressions from document images.

icdar, 02:956.

Kara, L. B. and Stahovich, T. F. (2004). Hierarchical pars-

ing and recognition of hand-sketched diagrams. In

UIST ’04: Proceedings of the 17th annual ACM sym-

posium on User interface software and technology,

pages 13–22, New York, NY, USA. ACM.

Lee, W., Kara, L. B., and Stahovich, T. F. (2007). An ef-

ﬁcient graph-based recognizer for hand-drawn sym-

bols. Comput. Graph., 31(4):554–567.

Li, M.-H. H. X.-D. T. N. (2006). Structural analysis of

printed mathematical expressions based on combined

strategy. Machine Learning and Cybernetics, 2006 In-

ternational Conference, pages 3354 – 3358.

Miller, E. G. and Viola, P. A. (1998). Ambiguity and con-

straint in mathematical expression recognition. Nat.

Conf. on Artif. Intell., pages 784–792.

Mori, S., Suen, C., , and Yamamoto, K. (1992). Historical

review of ocr research and development. Proceedings

of the IEEE, 80:1029–1058.

Nii, P. (1986). Blackboard systems part two: Blackboard

application systems. AI Mag., 7(3):82–106.

Rjean Plamond, S. N. S. (2000). On-line and off-line hand-

writing recognition: A comprehensive survey. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 22(1):63–84.

Smith, J. (1998). The Book. The publishing company, Lon-

don, 2nd edition.

BREADER: A MODULAR FRAMEWORK FOR VISION RECOGNITION OF MATHEMATICAL-LOGICAL

STRUCTURES

255