
OBLIGATORY HYBRID NETWORKS OF EVOLUTIONARY
PROCESSORS
Artiom Alhazov
Institute of Mathematics and Computer Science, Academy of Sciences of Moldova
Str. Academiei 5, MD-2028, Chis¸in˘au, Moldova
Gemma Bel-Enguix, Yurii Rogozhin
Rovira i Virgili University, Research Group on Mathematical Linguistics, Pl. Imperial T`arraco 1, 43005 Tarragona, Spain
Keywords:
Formal languages, Networks of evolutionary processors, Point mutations, Distributed computing, Circular
Post machines.
Abstract:
In this paper obligatory hybrid networks of evolutionary processors (a variant of hybrid networks of evolu-
tionary processors model) are proposed. In the obligatory hybrid network of evolutionary processors a node
discards the strings to which no operations are applicable. We show that such networks have the same com-
putability power as Turing machines only using one operation per node (deletion on the left end and insertion
on the right end of the string) no rewriting and no filters.
1 INTRODUCTION
Insertion, deletion, and substitution are fundamental
operations in formal language theory, their power and
limits have obtained much attention. Due to their
simplicity, language generating mechanisms based on
these operations are of particular interest. Networks
of evolutionary processors (NEPs, for short), intro-
duced in (Castellanos et al., 2001), are proper exam-
ples for distributed variants of these constructs. In
this case, evolutionary processors (language proces-
sors performing insertion, deletion, and substitution
of a symbol) are located at nodes of a virtual graph
and operate over sets or multisets of words. During
the functioning of the system, they rewrite the corre-
sponding collections of words and then re-distribute
the resulting strings according to a communication
protocol assigned to the system. The language de-
termined by the network is usually defined as the set
of words which appear at some distinguished node in
the course of the computation. These architectures
also belong to models inspired by cell biology, since
each processor represents a cell performing point mu-
tations of DNA and controlling its passage inside and
outside the cell through a filtering mechanism. It is
known that, by using an appropriate filtering mecha-
nism, NEPs with a very small number of nodes are
computationally complete computational devices, i.e.
they are as powerful as the Turing machines (see, for
example (Alhazov et al., 2006; Alhazov et al., 2007)).
Particularly interesting variants of these devices
are the so-called hybrid networks of evolutionary pro-
cessors (HNEPs), where each language processor per-
forms only one of the above operations on a certain
position of the words in that node. Furthermore, the
filters are defined by some variants of random-context
conditions, i.e., they check the presence/absence of
certain symbols in the words. The notion was intro-
duced in (Mart´ın-Vide et al., 2003). In (Csuhaj-Varj´u
et al., 2005) it was shown that, for an alphabet V,
HNEPs with 27+ 3·card(V) nodes are computation-
ally complete. A significant improvementof the result
can be found in (Alhazov et al., 2008a), where it was
proved that HNEPs with 10 nodes (irrespectively of
the size of the alphabet) reach the universalpower and
at last in (Alhazov et al., 2008b) it was showed that
HNEPs with 7 nodes can reach the universal power.
Notice, that the family of HNEPs with 2 nodes is not
computationally complete (Alhazov et al., 2008b).
In this paper, we consider new variant of HNEP,
so called Obligatory Network of Evolutionary Pro-
cessors (OHNEP shortly). The differences between
613
Alhazov A., Bel-Enguix G. and Rogozhin Y. (2009).
OBLIGATORY HYBRID NETWORKS OF EVOLUTIONARY PROCESSORS.
In Proceedings of the International Conference on Agents and Artificial Intelligence, pages 613-618
DOI: 10.5220/0001809106130618
Copyright
c
SciTePress

HNEP and OHNEP are:
1. in using deletion and substitution operations: a
node discards a string if no operations in node are
applicable to string (in HNEP case this string re-
mains in the node),
2. an underlying graph is directed graph (in HNEP
case this graph is undirected).
We underline that both differences are natural.
The first one allows us to have the uniform defini-
tions of the operations on a string, as opposed to con-
sidering two cases as in HNEPs (it is the set of re-
sults of the applications of the operation to all possi-
ble positions; the case when there are no such position
yields the empty set by definition). The second differ-
ence, that of generalization of the underlying graph to
be directed, is natural from the computational point
of view; moreover, since the loops are typically not
considered, it also seems relevant from the viewpoint
of the biological motivation that the communicating
channels are directed.
These differences allow to proof universality of
OHNEP with nodes with only one operation, with-
out input and output filters and using only insertion
operation at the left end and deletion operation at the
right end of a string. This interesting fact stresses the
importance of structure of HNEP in order to reach
universality. On the other hand we can avoid substi-
tution operation. Notice that this feature of OHNEP
to discard a string if this string does not participate
at the operations has counterpart in DNA comput-
ing area, TVDH systems also discard strings if they
do not participate at splicing operations (Margenstern
et al., 2004).
A task to find a minimal number of nodes of uni-
versal OHNEP is open. A variant of OHNEP with un-
derlying complete graph is not considered yet. An im-
plementation of HNEPs and OHNEPs in mathemati-
cal linguistics is also interesting task to investigate.
2 DEFINITIONS
We recall some notions we shall use throughout the
paper. An alphabet is a finite and nonempty set of
symbols. The cardinality of a finite set A is written
as card(A). A sequence of symbols from an alphabet
V is called a word over V. The set of all words over
V is denoted by V
∗
and the empty word is denoted
by ε; we use V
+
= V
∗
\ {ε}. The length of a word
x is denoted by |x|, while we denote the number of
occurrences of a letter a in a word x by |x|
a
. For each
nonempty word x, alph(x) is the minimal alphabet W
such that x ∈ W
∗
.
Circular Post Machines (CPMs) were introduced
in (Kudlek and Rogozhin, 2001b), where it was
shown that all introduced variants of CPMs are com-
putationally complete, and moreover, the same state-
ment holds for CPMs with two symbols. In (Kudlek
and Rogozhin, 2001a; Alhazov et al., 2002) several
universal CPMs of variant 0 (CPM0) having small
size were constructed, among them in (Alhazov et al.,
2002) a universal CPM0 with 6 states and 6 sym-
bols. In this article we use the deterministic variant
of CPM0s.
A Circular Post Machine is a quintuple
(Σ, Q, q
0
, q
f
, R) with a finite alphabet Σ where 0
is the blank, a finite set of states Q, an initial state
q
0
∈ Q, a terminal state q
f
∈ Q, and a finite set of
instructions R with all instructions having one of the
forms px → q (erasing the symbol read and cut off a
cell), px → yq (overwriting and moving to the right),
p0 → yq0 (overwriting and creation of a blank),
where x, y ∈ Σ and p, q ∈ Q.
The storage of this machine is a circular tape, the
read and write head move only in one direction (to
the right), and with the possibility to cut off a cell or
to create and insert a new cell with a blank.
In the following, we summarize the necessary no-
tions concerning obligatory evolutionary operations.
For an alphabet V, we say that a rule a → b, with
a, b ∈ V ∪ {ε} is a obligatory substitution operation
if both a and b are different from ε; it is a obliga-
tory deletion operation if a 6= ε and b = ε; and, it
is an (obligatory) insertion operation if a = ε and
b 6= ε. The set of all obligatory substitution, deletion,
and insertion operations over an alphabet V are de-
noted by Sub
V
, Del
V
, and Ins
V
, respectively. Given
such rules π, ρ, σ, and a word w ∈ V
∗
, we define the
following obligatory evolutionary actions of π, ρ, σ
on w: If π ≡ a → b ∈ Sub
V
, ρ ≡ a → ε ∈ Del
V
, and
σ ≡ ε → a ∈ Ins
V
, then
π
∗
(w) =
{ubv | w = uav, u, v ∈ V
∗
}
(1)
ρ
∗
(w) =
{uv | w = uav, u, v ∈ V
∗
}
(2)
ρ
r
(w) =
{u | w = ua}
(3)
ρ
l
(w) =
{v | w = av}
(4)
σ
∗
(w) =
{uav | w = uv, u, v ∈ V
∗
}
(5)
σ
r
(w) =
{wa}
(6)
σ
l
(w) =
{aw}
(7)
Notice, that in (1) – (4) a result of obligatory evo-
lution operation may be empty set (this is the main
difference between obligatory hybrid network of evo-
lutionary processors and hybrid network of evolution-
ary processors).
ICAART 2009 - International Conference on Agents and Artificial Intelligence
614

Symbol α ∈ {∗, l, r} denotes the way of applying
an insertion or a deletion rule to a word, namely, at
any position (a = ∗), in the left-hand end (a = l),
or in the right-hand end (a = r) of the word, respec-
tively. Note that a substitution rule can be applied at
any position. For everyrule σ, action α ∈ {∗, l, r}, and
L ⊆V
∗
, we define the α−action of σ on L by σ
α
(L) =
S
w∈L
σ
α
(w). For a given finite set of rules M, we de-
fine the α − action of M on a word w and on a lan-
guage L by M
α
(w) =
S
σ∈M
σ
α
(w) and M
α
(L) =
S
w∈L
M
α
(w), respectively.
Before turning to the notion of an evolutionary
processor, we define the filtering mechanism.
For disjoint subsets P, F ⊆ V and a word w ∈ V
∗
,
we define the predicate ϕ (ϕ
(2)
in terminology of
(Csuhaj-Varj´u et al., 2005)) as ϕ(w;P, F) ≡ alph(w)∩
P 6=
/
0 ∧ F ∩ alph(w) =
/
0. The construction of this
predicate is based on random-context conditions de-
fined by the two sets P (permitting contexts) and F
(forbidding contexts). For every language L ⊆ V
∗
we
define ϕ(L, P, F) = {w ∈ L | ϕ(w;P, F)}.
An obligatory evolutionary processor over V is a
5-tuple (M, PI, FI, PO, FO) where:
- Either M ⊆ Sub
V
or M ⊆ Del
V
or M ⊆ Ins
V
. The
set M represents the set of obligatory evolutionary op-
erations of the processor. Note that every processor
is dedicated to only one type of the above obligatory
evolutionary operations.
- PI, FI ⊆ V are the input permitting/forbidding
contexts of the processor, while PO, FO ⊆ V are the
output permitting/forbidding contexts of the proces-
sor.
We denote the set of obligatory evolutionary proces-
sors overV by OEP
V
.
Definition 2.1 An obligatory hybrid network of evo-
lutionary processors (an OHNEP, shortly) is a 7-tuple
Γ = (V, G, N,C
0
, α, β, i
0
), where the following condi-
tions hold:
- V is an alphabet.
- G = (X
G
, E
G
) is a directed graph with set of ver-
tices X
G
and set of edges E
G
. G is called the underly-
ing graph of the network.
- N : X
G
−→ OEP
V
is a mapping which associates
with each node x ∈ X
G
the obligatory evolutionary
processor N(x) = (M
x
, PI
x
, FI
x
, PO
x
, FO
x
).
- C
0
: X
G
−→ 2
V
∗
is a mapping which identifies
the initial configuration of the network. It associates
a finite set of words with each node of the graph G.
- α : X
G
−→ {∗, l, r}; α(x) defines the action mode
of the rules performed in node x on the words occur-
ring in that node.
- β : X
G
−→ {(1), (2)} defines the type of the in-
put/output filters of a node. More precisely, for every
node, x ∈ X
G
, we define the following filters: the input
filter is given as ρ
x
(·) = ϕ
β(x)
(·;PI
x
, FI
x
), and the out-
put filter is defined as τ
x
(·) = ϕ
β(x)
(·, PO
x
, FO
x
). That
is, ρ
x
(w) (resp.τ
x
) indicates whether or not the word
w can pass the input (resp. output) filter of x. More
generally, ρ
x
(L) (resp. τ
x
(L)) is the set of words of L
that can pass the input (resp. output) filter of x.
- i
0
∈ X
G
is the output node of the OHNEP.
Notice, that in the definition of OHNEP above
G = (X
G
, E
G
) is a directed graph, but in the defini-
tion of HNEP (see, for example, (Csuhaj-Varj´u et al.,
2005)), underlying graph is an undirected graph. This
is the second difference between HNEP and OHNEP.
We say that card(X
G
) is the size of Γ. An OHNEP
is said to be a complete OHNEP, if its underlying
graph is a complete graph.
A configuration of an OHNEP Γ, as above, is
a mapping C : X
G
−→ 2
V
∗
which associates a set
of words with each node of the graph. A compo-
nent C(x) of a configuration C is the set of words
that can be found in the node x in this configura-
tion, hence a configuration can be considered as the
sets of words which are present in the nodes of the
network at a given moment. A configuration can
change either by an evolutionary step or by a com-
munication step. When it changes by an evolution-
ary step, then each component C(x) of the config-
uration C is changed in accordance with the set of
evolutionary rules M
x
associated with the node x and
the way of applying these rules α(x). Formally, the
configuration C
′
is obtained in one evolutionary step
from the configuration C, written as C =⇒ C
′
, iff
C
′
(x) = M
α(x)
x
(C(x)) for all x ∈ X
G
.
When it changes by a communication step, then
each language processor N(x), where x ∈ X
G
, sends
a copy of each of its words to every node processor
where the node is connected with x, provided that this
word is able to pass the output filter of x, and receives
all the words which are sent by processors of nodes
connected with x, providing that these words are able
to pass the input filter of x. Formally, we say that con-
figuration C
′
is obtained in one communication step
from configuration C, written as C ⊢ C
′
, iff C
′
(x) =
(C(x) −τ
x
(C(x)))∪
S
(y,x)∈E
G
(τ
y
(C(y) ∩ρ
x
(C(y))) for
all x ∈ X
G
.
For an OHNEP Γ, a computation in Γ is a se-
quence of configurations C
0
, C
1
,C
2
, . . . , where C
0
is the initial configuration of Γ, C
2i
=⇒ C
2i+1
and
C
2i+1
⊢ C
2i+2
, for all i > 0. If we use OHNEPs as
language generating devices, then the generated lan-
guage is the set of all words which appear in the out-
put node at some step of the computation. Formally,
the language generated by Γ is L(Γ) =
S
s≥0
C
s
(i
0
).
OBLIGATORY HYBRID NETWORKS OF EVOLUTIONARY PROCESSORS
615

3 MAIN RESULT
Theorem 1 Any CPM0 P can be simulated by an
OHNEP P
′
, where obligatory evolution processors
are with empty input and output filters and only inser-
tion and obligatory deletion operations in right and
left modes are used (without obligatory substitution
operations).
Proof. Let us consider a CPM0 P with symbols a
j
∈
Σ, j ∈ J = {0, 1. . . , n}, a
0
= 0 is a blank symbol, and
states, q
i
∈ Q, i ∈ I = {1, 2, . . . , f} , where q
1
is the
initial state and the only terminal state is q
f
∈ Q. We
suppose that P stops in the terminal state q
f
on every
symbol, i.e., there are instructions q
f
a
j
→ Halt, a
j
∈
J. (Notice, that it is easy to transform any CPM0 P
into a CPM0 P
′
that stops on every symbol in terminal
state.)
So, we consider CPM0 P with the set R of instruc-
tions of the forms q
i
a
j
−→ q
l
, q
i
a
j
−→ a
k
q
l
, q
i
0 −→
a
k
q
l
0, q
f
a
j
−→ Halt, where q
i
∈ Q \ {q
f
}, q
l
∈ Q,
a
j
, a
k
∈ Σ. A configuration w = q
i
a
j
W of CPM0 P de-
scribes that P in state q
i
∈ Q considers symbol a
j
∈ Σ
on the left-hand end of W ∈ Σ
∗
.
Now we construct an OHNEP P
′
simulating P.
To simplify the description of P
′
, we use hq
f
a
j
i and
hq
f
a
j
i
1
, j ∈ J as aliases of houti.
P
′
= (V,G, N,C
0
, α, β, i
0
),
V = {q
1
} ∪ Σ,
G = (X
G
, E
G
),
X
G
= {hiniti,houti}
∪ {hq
i
a
j
i | (q
i
a
j
→ u) ∈ R}
∪ {hq
i
a
j
i
1
| (q
i
a
j
→ a
k
u) ∈ R},
E
G
= {(hiniti,hq
1
a
j
i) | j ∈ J}
∪ {(hq
i
a
j
i, hq
l
a
k
i)
| (q
i
a
j
→ q
l
) ∈ R, k ∈ J}
∪ {(hq
i
a
j
i, hq
i
a
j
i
1
) | (q
i
a
j
→ a
k
u) ∈ R}
∪ {(hq
i
a
j
i
1
, hq
l
a
s
i)
| (q
i
a
j
→ a
k
q
l
) ∈ R, s ∈ J}
∪ {(hq
i
0i
1
, hq
l
0i
1
) | (q
i
0 → a
k
q
l
0) ∈ R},
C
0
(x) = {q
1
W}, if x = hiniti,
where W is the input of P,
C
0
(x) =
/
0, x ∈ X
G
\ {hiniti},
β(x) = 2, x ∈ X
G
,
N(x) = (M
x
,
/
0,
/
0,
/
0,
/
0), x ∈ X
G
,
M
x
= {q
1
→ ε}, x = hiniti,
M
x
= {a
j
→ ε}, x = hq
i
a
j
i,
M
x
= {ε → a
k
}, x = hq
i
a
j
i
1
,
where (q
i
a
j
→ a
k
u) ∈ R,
α(x) = l, if M
x
= {a → ε},
α(x) = r, if M
x
= {ε → a}, or M
x
=
/
0.
OHNEP P
′
will simulate every computation step
performed by CPM0 P with a sequence of computa-
tion steps in P
′
.
Let q
1
a
j
W
0
be the initial configuration of CPM0
P. We present this configuration in node hiniti of
OHNEP P
′
as word q
1
a
j
W
0
. Obligatory evolution
processor, associated with this node is N(hiniti) =
({(q
1
→ ε)
l
},
/
0,
/
0,
/
0,
/
0). In the following we will omit
complete description of obligatory evolution proces-
sor, and will present only obligatory evolution oper-
ation. Further word a
j
W
0
from node hiniti will be
passed to nodes hq
1
a
j
i, j ∈ J.
If the computation in P is finite, then the final con-
figuration q
f
W of P will appear at node houti of P
′
as
a string W, moreover, any string W that can appear at
node houti corresponds to a final configuration q
f
W
of P. In the case of an infinite computation in P, no
string will appear in node houti of P
′
and the compu-
tation in P
′
will never stop.
Now we describe nodes of OHNEP P
′
, connec-
tions between them and obligatory evolutionary oper-
ations, associated with these nodes. Let I
′
= I \ { f}.
1. Node hq
i
a
j
i with operation (a
j
→ ε)
l
, i ∈ I
′
, j ∈
J.
Let word a
t
W, t ∈ J, W ∈ Σ
∗
appear in this node.
If j 6= t then this word a
t
W will be discarded and
on the next communication step node hq
i
a
j
i will
send nothing. If j = t then the node sends W to
nodes {hq
l
a
k
i | k ∈ J} or hq
i
a
j
i
1
.
• Instruction of P is q
i
a
j
−→ q
l
, i ∈ I
′
, j ∈
J, l ∈ I. Node hq
i
a
j
i is connected with nodes
{hq
l
a
k
i | k ∈ J}.
• Instructions of P is q
i
a
j
−→ a
k
q
l
or q
i
0 −→
a
k
q
l
0, i ∈ I
′
, j, k ∈ J, l ∈ I. Node hq
i
a
j
i is con-
nected with node hq
i
a
j
i
1
.
2. Node hq
i
a
j
i
1
, i ∈ I
′
, j ∈ J with operation (ε →
a
k
)
r
receives word W and sends word Wa
k
to
nodes {hq
l
a
s
i | s ∈ J} or hq
l
0i
1
.
• Instructions of P is q
i
a
j
−→ a
k
q
l
, i ∈ I
′
, j, k ∈
J, l ∈ I. Node hq
i
a
j
i
1
is connected with nodes
{hq
l
a
s
i | s ∈ J}.
• Instruction of P is q
i
0 −→ a
k
q
l
0, i ∈ I
′
, k ∈
J, l ∈ I. Node hq
i
0i
1
is connected with node
hq
l
0i
1
.
Again in all cases, we mean houti whenever we
write hq
f
a
j
i or hq
f
a
j
i
1
, j ∈ J.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
616
Now we describe simulation of instructions of
CPM0 P by OHNEP P
′
.
Instruction q
i
a
j
−→ q
l
: q
i
a
j
W
P
−→ q
l
W.
Let word a
t
W, where t ∈ J, W ∈ Σ
∗
, i ∈ I
′
appears
in node hq
i
a
j
i. If t 6= j, string a
t
W will be discarded;
if t = j, string W will be passed to nodes {hq
l
a
j
i |
j ∈ J} . If l = f, the final configuration q
f
W of P
will appear in the output node houti as W. This is the
result. So, we simulated instruction q
i
a
j
−→ q
l
in a
correct manner.
Instruction q
i
a
j
−→ a
k
q
l
: q
i
a
j
W
P
−→ q
l
Wa
k
.
Let word a
t
W, where t ∈ J, W ∈ Σ
∗
, i ∈ I
′
ap-
pears in node hq
i
a
j
i. If t 6= j, string a
t
W will be
discarded; if t = j string W will be passed to node
hq
i
a
j
i
1
. Node hq
i
a
j
i
1
receives this word and sends
word Wa
k
to nodes hq
l
a
s
i, s ∈ J. If l = f, the final
configuration q
f
Wa
k
of P will appear in the output
node houti as Wa
k
. This is the result. So, we simu-
lated instruction q
i
a
j
−→ a
k
q
l
in a correct manner.
Instruction q
i
0 −→ a
k
q
l
0: q
i
0W
P
−→ q
l
0Wa
k
.
Let word a
t
W, where t ∈ J, W ∈ Σ
∗
, i ∈ I
′
appears
in node hq
i
0i. If a
t
6= 0, string a
t
W will be discarded;
if a
t
= 0, string W will be passed to node hq
i
0i
1
. It re-
ceives this word and sends word Wa
k
to node hq
l
0i
1
.
If l = f , the final configuration q
f
0Wa
k
of P will ap-
pear in the output node houti as a word Wa
k
. This is
the result (we can avoid the case of missing symbol 0
if the simulated CPM0 is modified to only halt by in-
structions of previous types). In case l 6= f, word Wa
k
will be passed to the node hq
l
0i
1
, which correspond to
the configuration of P which has “just read” symbol 0
in state q
l
. So, we simulated instruction q
i
0 −→ a
k
q
l
0
in a correct manner.
So, CPM0 P is correctly modeled. We have
demonstrated that the rules of P are simulated in P
′
.
The proof that P
′
simulates only P comes from the
construction of the rules in P
′
, we leave the details to
the reader.
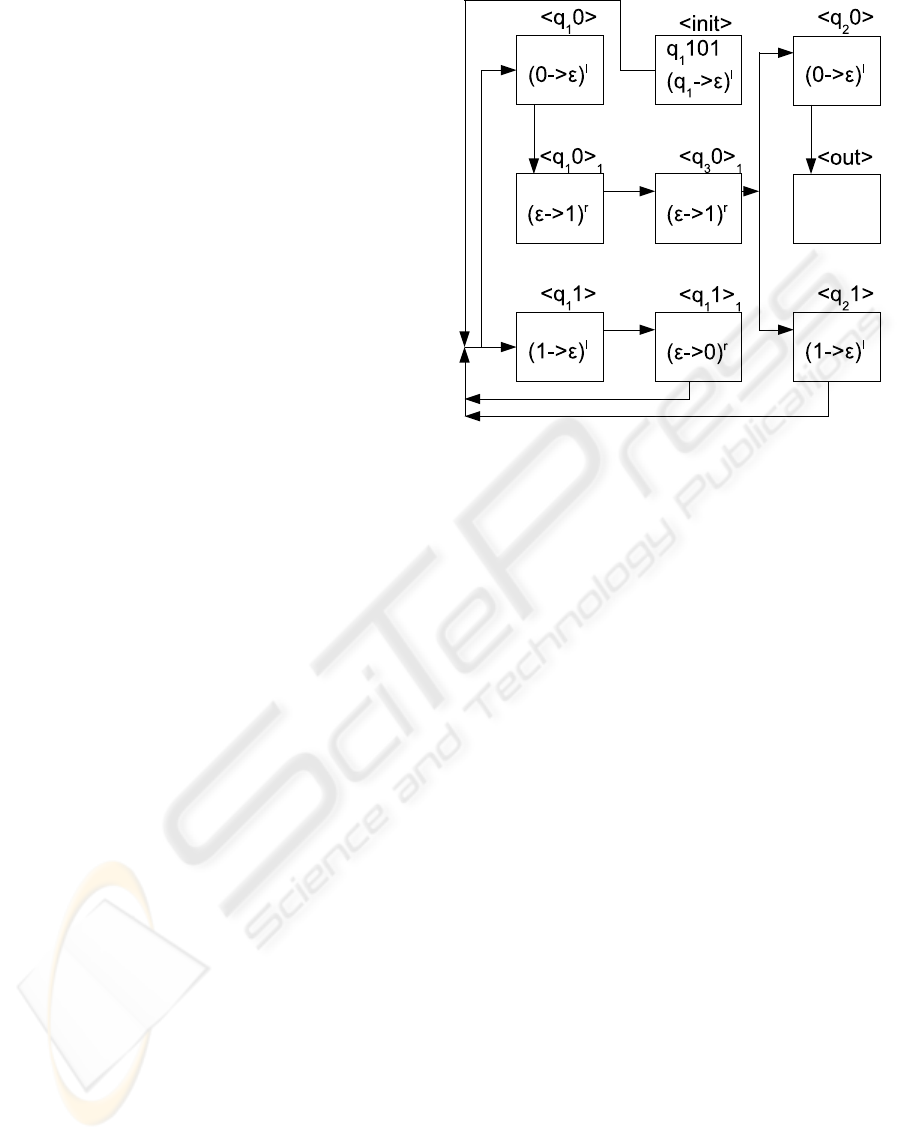
Example 3.1 Consider the following CPM0: M =
({0, 1}, {q
1
, q
2
, q
3
, q
f
}, q
1
, q
f
, P) with the following
commands (we do not list a command with q
3
1 on the
left because it is not reachable).
q
1
0 → 1q
3
0 q
2
0 → q
f
q
3
0 → 1q
2
q
1
1 → 0q
1
q
2
1 → q
1
We illustrate the work of M as follows. It trans-
forms 101 into 011 in 13 steps: q
1
101 ⇒ q
1
010 ⇒
q
3
0101 ⇒ q
2
1011 ⇒ q
1
011 ⇒ q
3
0111 ⇒ q
2
1111 ⇒
Figure 1: The OHNEP constructed from M.
q
1
111 ⇒ q
1
110 ⇒ q
1
100 ⇒ q
1
000 ⇒ q
3
0001 ⇒
q
2
0011 ⇒ q
f
011.
We now present an OHNEP Γ constructed from M.
Γ = (V, G, N,C
0
, α, β, i
0
),
V = {q
1
, 0, 1},
C
0
(hiniti) = {q
1
W}, where W is the input of M,
C
0
(x) =
/
0, x ∈ X
G
\ {hiniti},
β(x) = 2, x ∈ X
G
,
N(x) = (M
x
,
/
0,
/
0,
/
0,
/
0), x ∈ X
G
,
and G is given in Figure 1, together with (M
x
)
α(x)
for
all nodes x ∈ X
G
(we omitted the node hq
3
0i because
it is not reachable).
Corollary 3.1 A family of OHNEPs with obligatory
evolutionary processors with empty filters and evo-
lutionary insertion in the right mode and deletion in
the left mode (without substitution) is computationally
complete.
Corollary 3.2 There exists a universal OHNEP with
obligatory evolutionary processors with empty filters
and evolutionary insertion in the right mode and dele-
tion in the left mode and with 65 nodes.
Proof. Let us consider the smallest known universal
CPM0 P with 6 states and 6 symbol (Alhazov et al.,
2002). We add special halt state to the program of
this machine in order to stop on every symbol of the
machine. So, CPM0 P will be with 7 states and 6
symbols. Now we construct OHNEP P
′
according al-
gorithm in the theorem above and we get 65 nodes.
OBLIGATORY HYBRID NETWORKS OF EVOLUTIONARY PROCESSORS
617

4 CONCLUSIONS
We have considered new variant of Hybrid Network
of Evolutionary Processors - Obligatory Hybrid Net-
work of Evolutionary Processors. The differences be-
tween them are in underlying graph (undirected graph
in HNEP case and directed graph in OHNEP case)
and using of operations, OHNEP discards a string if
operations at the node are not applicable to the string
(in HNEP case the string remains in the node). We
showed that OHNEPs with empty input and output
filters and insertion operation at the right end and
obligatory deletion operation on the left end of the
string (without substitution operation) can carry out
an universal computation, and there exists universal
OHNEP with 65 nodes. Notice, that
structure
of
OHNEP (underlying directed graph) and obligatory
of operation deletion allows to avoid filters and sub-
stitution operation and to reach universality. Several
questions are opened, in particularly question about
computational power of OHNEPs with underlying
complete graph and question about universal OHNEP
with minimal number of nodes.
ACKNOWLEDGEMENTS
The first and the third authors acknowledge the Sci-
ence and Technology Center in Ukraine, project 4032
and the third author acknowledges the support of
European Commission, project MolCIP, MIF1-CT-
2006-021666.
REFERENCES
Alhazov, A., Csuhaj-Varj´u, E., Mart´ın-Vide, C., and Ro-
gozhin, Y. (2008a). About universal hybrid networks
of evolutionary processors of small size. In Pro-
ceedings of the 2nd International Conference on Lan-
guage and Automata Theory and Applications, LATA
2008, pages 28–39. Lecture notes in Computer Sci-
ence 5196, Springer.
Alhazov, A., Csuhaj-Varj´u, E., Mart´ın-Vide, C., and Ro-
gozhin, Y. (2008b). Computational completeness of
hybrid networks of evolutionary processors with seven
nodes. In Proceedings of DCFS 2008 (10th Interna-
tional Workshop on Descriptional Complexity of For-
mal Systems). Charlottetown, Canada.
Alhazov, A., Kudlek, M., and Rogozhin, Y. (2002). Nine
universal circular post machines. Computer Science
Journal of Moldova, 10 (3):247–262.
Alhazov, A., Mart´ın-Vide, C., and Rogozhin, Y. (2006). On
the number of nodes in universal networks of evolu-
tionary processors. Acta Informatica, 43 (5):331–339.
Alhazov, A., Mart´ın-Vide, C., and Rogozhin, Y. (2007).
Networks of evolutionary processors with two nodes
are unpredictable. In Pre-Proceedings of the 1st In-
ternational Conference on Language and Automata
Theory and Applications, LATA 2007, pages 521–528.
GRLMC report 35/07, Rovira i Virgili University, Tar-
ragona.
Castellanos, J., Mart´ın-Vide, C., Mitrana, V., and Sempere,
J. (2001). Solving np-complete problems with net-
works of evolutionary processors. In Proceedings of
IWANN 2001, pages 521–528. Lecture Notes in Com-
puter Science 2084, Springer.
Csuhaj-Varj´u, E., Mart´ın-Vide, C., and Mitrana, V. (2005).
Hybrid networks of evolutionary processors are com-
putationally complete. Acta Informatica, 41 (4-
5):257–272.
Kudlek, M. and Rogozhin, Y. (2001a). New small universal
circular post machines. In Proceedings of FCT 2001,
pages 217–227. Lecture Notes in Computer Science
2138, Springer.
Kudlek, M. and Rogozhin, Y. (2001b). Small universal cir-
cular post machines. Computer Science Journal of
Moldova, 9 (1):34–52.
Margenstern, M., Rogozhin, Y., and Verlan, S. (2004).
Time-varying distributed h systems with parallel com-
putations: The problem is solved. In Proceedings of
DNA 9, pages 48–54. Lecture Notes in Computer Sci-
ence 2943, Springer.
Mart´ın-Vide, C., Mitrana, V., P´erez-Jim´enez, M., and
Sancho-Caparrini, F. (2003). Hybrid networks of evo-
lutionary processors. In Proceedings of GECCO 2003,
pages 401–412. Lecture Notes in Computer Science
2723, Springer.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
618
