
3D Segmentation for the Study of Cell Cycle Progression
in Live Drosophila Embryos
Chinta Rambabu, Puah Wee Choo, Janos Kriston-Vizi and Martin Waser
Bioinformatics Institute, A*STAR
30 Biopolis Street, Matrix Building, Singapore 138671, Singapore
Abstract. We study the dynamics of cell division in live Drosophila embryos
using fluorescent proteins and 3D time-lapse microscopy. Accurate segmentation
of nuclei and mitotic chromosomes labeled by the live reporter histone-GFP is
a prerequisite for subsequent tracking and quantitative object analysis. We pro-
pose an automated 3D segmentation method based on narrow band level sets that
preserves the boundary of the cell nuclei and removes signals that are artifacts
of live cell imaging. We introduce an improved 3D narrow band approach in the
region shrinking and growing process for accurately segmenting the cell nuclei
from background. The proposed method has been evaluated with the ground truth
regarding the object level accuracy and segmentation quality. Both the object
level accuracy and pixel accuracy of the proposed method are around 96% and
85% respectively. Our algorithm can robustly segment nuclei and chromosomes
in different phase of the division cycle.
1 Introduction
Cell cycle regulation plays an important role in disease and development. Drosophila
embryogenesis is an excellent model system to study the mechanics and regulation of
cell division cycle in an intact multi-cellular organism [1]. The first 13 nuclear division
cycles are synchronous and take place in a common cytoplasm shared by all nuclei.
After completion of the syncytial blastoderm, cells form and all subsequent cell divi-
sions happen within the confines of cell membranes. Fluorescence proteins, such as
histone-GFP, in conjunction with 3D video microscopy can be applied to monitor cell
cycle progression in living cells. Quantitative analysis of 3D image stacks can provide
novel insights into the cell division cycle and its genetic regulation. However, computer
vision tasks like feature extraction, quantification, classification and tracking are highly
dependent on the accuracy of image segmentation.
Several automatic 3D segmentation methods [2–7] have been developed for seg-
mentation of cell nuclei. The most common methods used for cell nuclei segmentation
can be classified as watershed, model and active surface-based methods. Watershed-
based methods [2] [3] are very popular for segmentation of merged nuclei. However,
they are prone to over-segmentation and requiring complex postprocessing. Model-
based segmentation method [4] has demonstrated highest segmentation accuracy but
they rely on a priori model of the expected nuclei morphology. Moreover, various
Rambabu C., Wee Choo P., Kriston-Vizi J. and Waser M. (2009).
3D Segmentation for the Study of Cell Cycle Progression in Live Drosophila Embryos.
In Proceedings of the 1st International Workshop on Medical Image Analysis and Description for Diagnosis Systems, pages 43-51
DOI: 10.5220/0001813300430051
Copyright
c
SciTePress
active surface based methods [5–7] have been proposed for nuclear segmentation. In
the active surface-based methods, objects are represented as a smooth surface, which
evolves with a speed force depending on the geometric property of the surface and the
external energy. However, the active surface-based methods suffer from an inherent de-
pendency on the initial seed. Various methods exist in the literature [2–7]; all of which
have been developed under restricted environmental conditions and are motivated by
specific application problem.
In 3D live microscopy, various factors, including uneven illumination due to limited
depth penetration, photo-bleaching, poor signal-to-noise ratio (SNR), heterogeneity in
the localization of fluorescent molecules and other artifacts can affect the performance
of segmentation. In order to characterize the dynamic changes of nuclear and chromo-
somal morphology during the division cycles we propose a segmentation algorithm that
has to meet the following requirements: (1) recognition of various shapes and textures
in the different stages of interphase and mitosis, (2) recognition during different stages
of development and (3) robustness of the object detection against fluorescence signals
that are not associated with nuclei, e.g. lipid droplets. In this paper, we present a hybrid
3D segmentation method that aims to handle the above-mentioned challenges of nu-
clear segmentation. We also present experimental results and validation of the proposed
method.
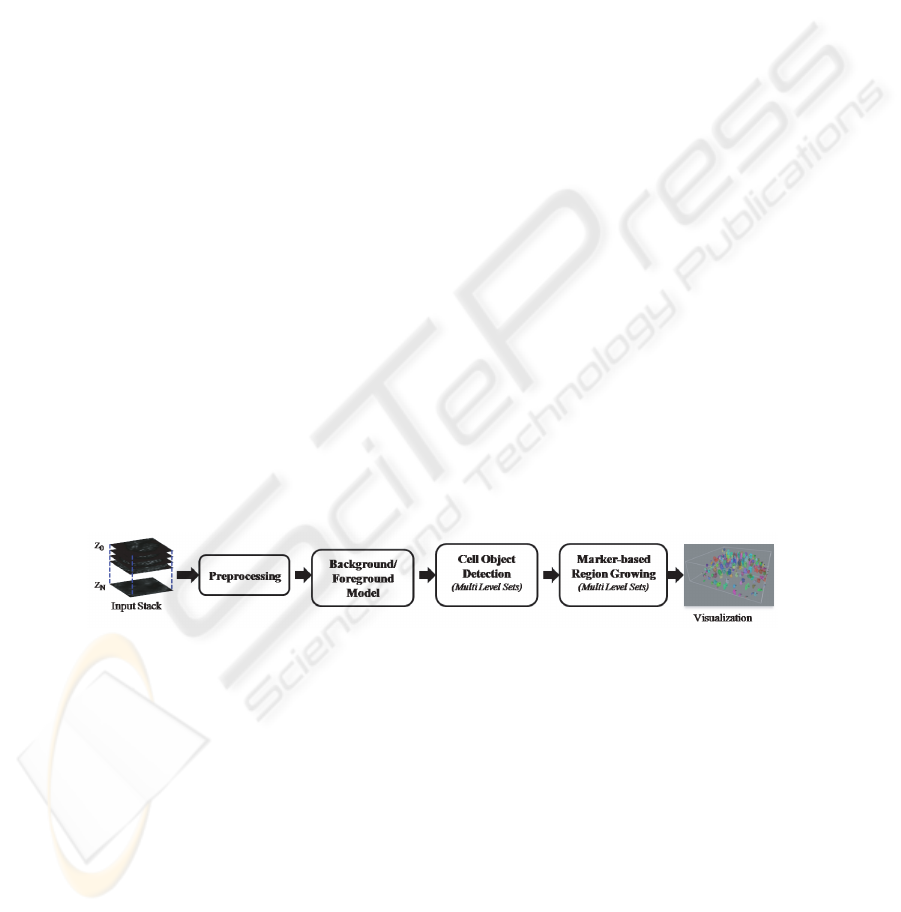
2 Hybrid 3D Segmentation Method
In this section, we describe an automated hybrid 3D segmentation approach that pre-
serves the surfaces of cell nuclei and is also robust against imaging artifacts inherent
to laser scanning confocal microscopy (LSM). The method is composed of a sequence
of four major steps; namely preprocessing, background/foreground model, cell object
detection and marker-based region growing (Figure 1). The detailed description of the
major steps is provided next.
Fig.1. Flow chart illustrating the major steps in the proposed method.
2.1 Image Acquisition
Cell nuclei and chromosomes in Drosophila embryos were labeled using the live flu-
orescence reporter histone H2Av-GFP [8] . Image acquisition was performed using an
inverted Zeiss 5 Live laser scanning confocal microscope and a 63x N.A. 1.3 oil immer-
sion lens. Drosophila embryos were dechorionated in 50% bleach and embedded in 1%
agarose on aglass bottom dish. Image de-convolution was carried using the Huygens
Professional, version 3.0.
44

2.2 Preprocessing
Serial optical sections produced by confocal microscopy tend to suffer from attenuation
of fluorescence signals in deeper tissue layers. In order to compensate for uneven illu-
mination within the same image stack, we use a simple method that normalizes pixel
intensity relative to the optical slice which shows the highest mean intensity. More-
over, live cell imaging records signals that are not associated with nuclei or chromo-
somes. These can be due to auto-fluorescence or cytoplasmic histone-GFP containing
lipid droplets [9]. Compared to cell nuclei, lipid droplets have a smaller size and differ
both in mean and standard deviation of intensity. A series of median filters was used
to alleviate the problem. However, variable window size filtering altered the shape of
object boundaries and increased false detection rate. To overcome this problem, we in-
troduced a novel pre-processing method based on 3D morphologicalreconstruction[10]
that enhances the background noise and limits debris. We performed 3D morphological
reconstruction that preserves object boundaries, followed by multi-scale gradient and
local minima elimination that limits the debris by varying the height parameter h. The
parameter h used for reducing debris needs to be specified manually as its appropriate
value depends on the nature of variation of gray values in the debris.
2.3 Background/Foreground Detection
The background/foreground detection starts with the detection of plateau minima in
the gradient stack and then, labels the largest minima of height h as background and
the others as foreground. At last, we applied a fast hillclimbing technique [11] on all
optical slices simultaneously.
2.4 Cell Object Detection
This section describes the cell object detection in the image stack by region shrinking
based on the Narrow Band level set (NB) approach [12] [13]. The basic idea of the
narrow band level set concept is to update level sets and the driving force in a subset of
points in the neighborhood of evolving front instead of the points on the grid. The nar-
row band has to be updated in each iteration and where it searches for closest front point
over the entire fixed narrow band for computing front driving force. The time complex-
ity of the NB method is O(δn
4
), where n is the number of grid points along a side and
δ is the width of narrow band. The conventional NB approach, however, is impractical
for high-throughput or large scale 3D nuclei segmentation. In the proposed approach,
we aim at update the level set in the nearest neighboring points (26-connected) of the
deforming front points and define an appropriate speed function F that can accelerate
the evolving surface to the desired object boundary.
We use an implicit representation of the surface S as the zero level set of higher di-
mensional time-varying function Φ(S) = 0. The surface evolution equation as follows,
∂Φ(S)
∂t
=
∂S
∂t
· ∇Φ +
∂Φ
∂t
⇒
∂Φ
∂t
= −F |∇Φ| (1)
45
Where F is the speed function normal to the surface S. The formulation of modified
speed function is
F = R −εK (2)
Where R is an unit sign function (+1 for object region and -1 for background) that
makes the object surface inflate or deflate. The signed value R(p) at pixel p ∈ D
I
can
be obtained
R(p) =
+1 if (I(p) > T
i
) then
−1 Otherwise
, T
i
∈ [µ
B
+ kσ
B
, µ
O
i
− kσ
O
i
] (3)
Here T
i
is an optimal threshold value [14] between the background model (µ
B
, σ
B
) and
the candidate object model(µ
O
i
, σ
O
i
) . The viscosity term -εK reduces the curvature
of the surface. Where K is the mean curvature of the evolving surface S and ε is a non-
negative regularization parameter. The mean curvature K of surface can be formulated
as
K = ∇ ·
∇Φ
|∇Φ|
=
ˆ
∆
x
Φ +
ˆ
∆
y
Φ +
ˆ
∆
z
Φ =
−→
n
+
−
−→
n
−
,
where
−→
n
+
=
D
x
+
√
(D
x
+
)
2
+(D
y
c
)
2
+(D
z
c
)
2
+ζ
D
y
+
√
(D
x
c
)
2
+(D
y
+
)
2
+(D
z
c
)
2
+ζ
D
z
+
√
(D
x
c
)
2
+(D
y
c
)
2
+(D
z
+
)
2
+ζ
−→
n
−
=
D
x
−
√
(D
x
−
)
2
+(D
y
c
)
2
+(D
z
c
)
2
+ζ
D
y
−
√
(D
x
c
)
2
+(D
y
−
)
2
+(D
z
c
)
2
+ζ
D
z
−
√
(D
x
c
)
2
+(D
y
c
)
2
+(D
z
−
)
2
+ζ
D
x
+
= Φ
x
+
- Φ
x
c
, D
x
−
= Φ
x
c
- Φ
x
−
and D
x
c
=
Φ
x
+
−Φ
x
−
2
represent forward, backward and
center gradients in x direction, and similarly for y and z directions.
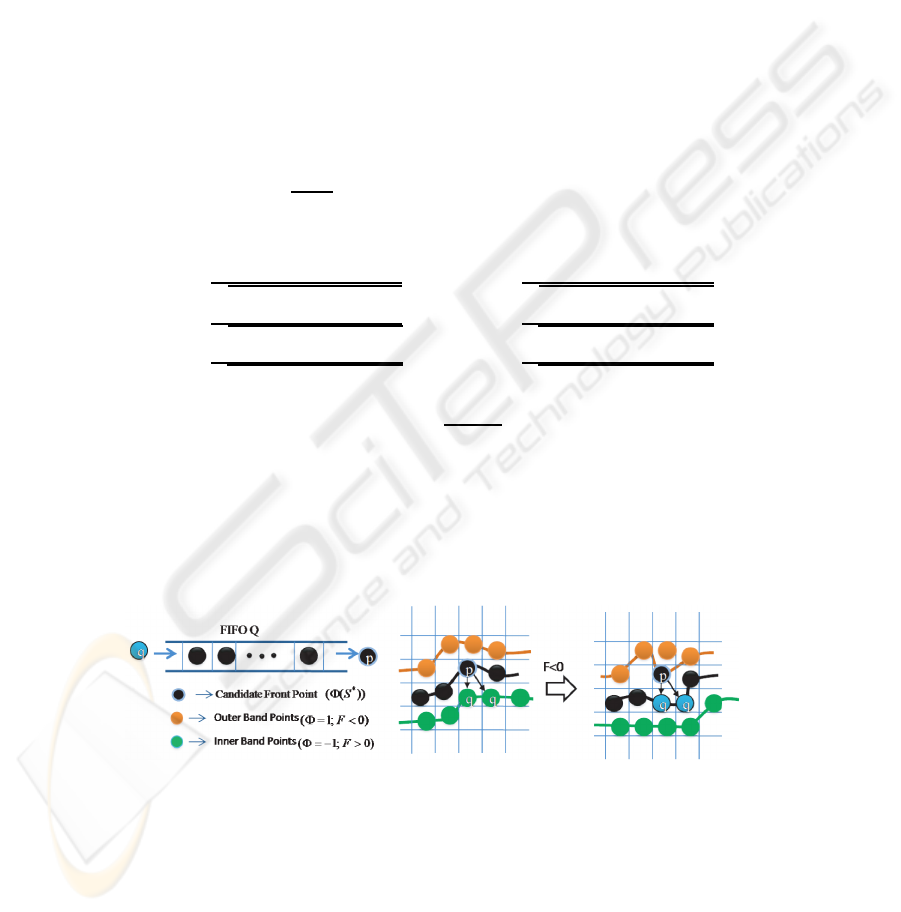
We utilize a FIFO queue for recursive region shrinking in depth-first order from
initial foreground front points as shown in Fig.2. First, we initialize the 3D level sets
Φ with +1 for background and -1 for foreground region, and then, initialize the FIFO
queue Q with the foreground points (Φ = −1 ) which have at least one outer band point
(background, Φ = 1).
Fig.2. Queue-based region shrinking at candidate front points.
In each iteration, points in the queue Q are processed, and the connected elements
and object models are updated. Point p ∈ D
I
is de-queued from queue Q one at a time
and its surface driving force F is calculated as given in equation 2. If the force F is less
46
than zero, then the candidate point p becomes background (Φ=1) and its neighboring
object points with level set value equal to -1 are inserted into the queue Q for recursive
region shrinking process. Otherwise, if the force F at point p is greater than zero, then
the candidate point p becomes cell object boundary point. This process is iterated until
the criterion is satisfied. The complexity of proposed approach is linear with respect to
the number of neighboring grid points. The total number of operations per iteration is
bound by n ∗ N
26
G
, here N
26
G
stands for 26-connected neighbors on the 3D grid and n
is the number of evolving surface front points. Hence, the proposed approach limits the
search range with in N
26
G
points at each candidate surface front point against δn
2
points
for narrow band methods.
2.5 Marker-based Region Growing
In this section, we introduce a fast marker-based 3D region growing method for sepa-
rating the merged cells that are extracted in the cell object detection step. The proposed
method consists of two sequential steps, namely 3D marker detection and 3D region
growing. In the marker detection step, we use conditional binary morphologicalerosion
based on the hypothesis test followed by volume-based filtering. The proposed marker
detection technique well identifies the markers in the cell object and also detects sep-
arate markers for merged cells in the image stack. The proposed 3D region growing
method starts from the labeled 3D marker and then, grows the region by surface defor-
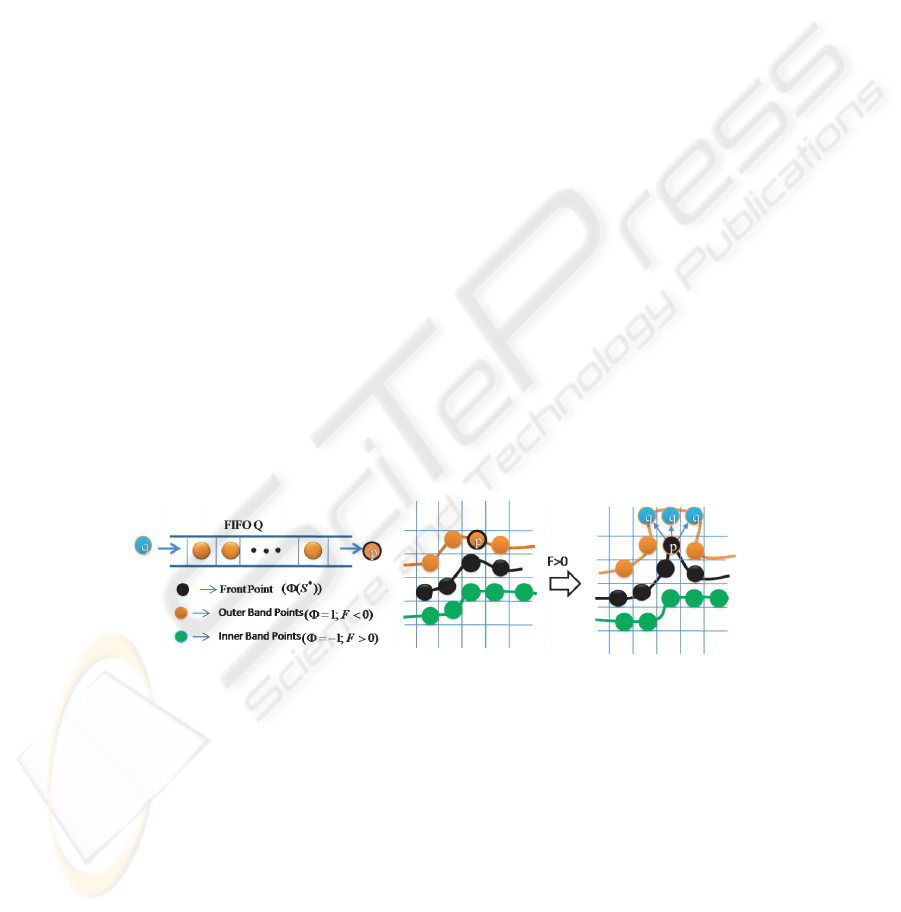
mation, simultaneously in all the markers. We use a FIFO queue for recursive 3D region
growing in depth-first order from initial 3D object markers as shown in Fig. 3.
First, we label the object markers in 3D by using connect component labeling where
each marker get unique label and then, initialize the 3D level sets Φ with +1 for back-
ground and -1 for 3D object marker and the FIFO queue Q with the outer band points
(Background, Φ=1) which have at least one marker object point (Marker, Φ=-1).
Fig.3. Queue-based region growing at candidate outer points.
Outer band point p ∈ D
I
is de-queued from queue Q one at a time and its sur-
face driving force F is calculated as given in equation 2. If the force F at point p is
greater than zero, then we decide the label of candidate point p based on its neighboring
surface front points. If the candidate p has neighboring surface front points which are
originated from same marker, then the outer band point p becomes surface front point
and its neighboring outer band points q ∈ N
G
(p) with level set value equal to 1 are
inserted into the queue Q for recursive region growing process. However, if the point p
47

has surface front neighbors which are originated from different markers, then, the point
p gets a watershed label which is used to separate the adjacent surface fronts. Other-
wise, if the force F at point p is less than zero, then, the candidate point p becomes
background. The present iteration completes when all the points in the queue visited. In
the each iteration, we update the object models. This process is iterated until the crite-
rion is satisfied. Finally, we apply an isotropic and discrete Gaussian shape filter of size
(3×3× 3) on the 3D level set for smoothening the surface points.
3 Experimental Results
We performed a set of experiments to evaluate the proposed 3D segmentation method
for the detection of cell nuclei in Live Drosophila Embryos time-lapse images. We
tested our segmentation on image stacks acquired during different stages of embryonic
development; the synchronous nuclear cycles of the syncytial blastoderm and mitotic
domains of the post-cellular blastoderm that contain mixtures of different phases of
the cell cycle. Figure 4 illustrates the experimental results obtained from applying the
proposed 3D segmentation method for post-cellular blastoderm time-lapse images. The
method has been evaluated by manually creating ground truth, developed by automatic
thresholding on image stack followed by manual correction on individual cells by using
ImageJ plugin. We evaluated the segmentation results based on the object level accuracy
such as number of correctly classified cells, merged cells and split cells, and pixel level
detection rates, namely miss detection rate and false alarm rate. The accuracy of our
approach was evaluated for image data recorded during different stages of development
(Table 1). On average, 96% of 3D cell nuclei were identified. The segmentation quality
on the pixel level ranged between 85%-90%. Figure 5 shows a mitotic nucleus track
from interphase to the end of anaphase in wildtype syncytium.
Table 1. The performance of proposed method in Live Drosophila Embryos time-lapse images.
Object level accuracy Pixel level
Image Stack No. of Correct Merged False Split Accuracy
(70 slices) cell nuclei cells cells Positives cells
Post-cellular 192 187 1 13 6 86.45%
blastoderm
Syncytial 96 96 0 1 0 88.67%
blastoderm
48

(a)
(b)
(c)
(d)
(e)
(f)
Fig.4. Automatic segmentation of cell nuclei in images acquired during the post-cellular blasto-
derm of embryogenesis. (a) Original optical slice 15, (c) original optical slice 25, (e) Maximum
Intensity Projection (MIP) of original image stack. Segmentation results of optical slices 15 (b)
and 25 (d). Contours of detected regions of interest are shown in white. (f) 3D visualization of
segmented cell nuclei and their labels.
49
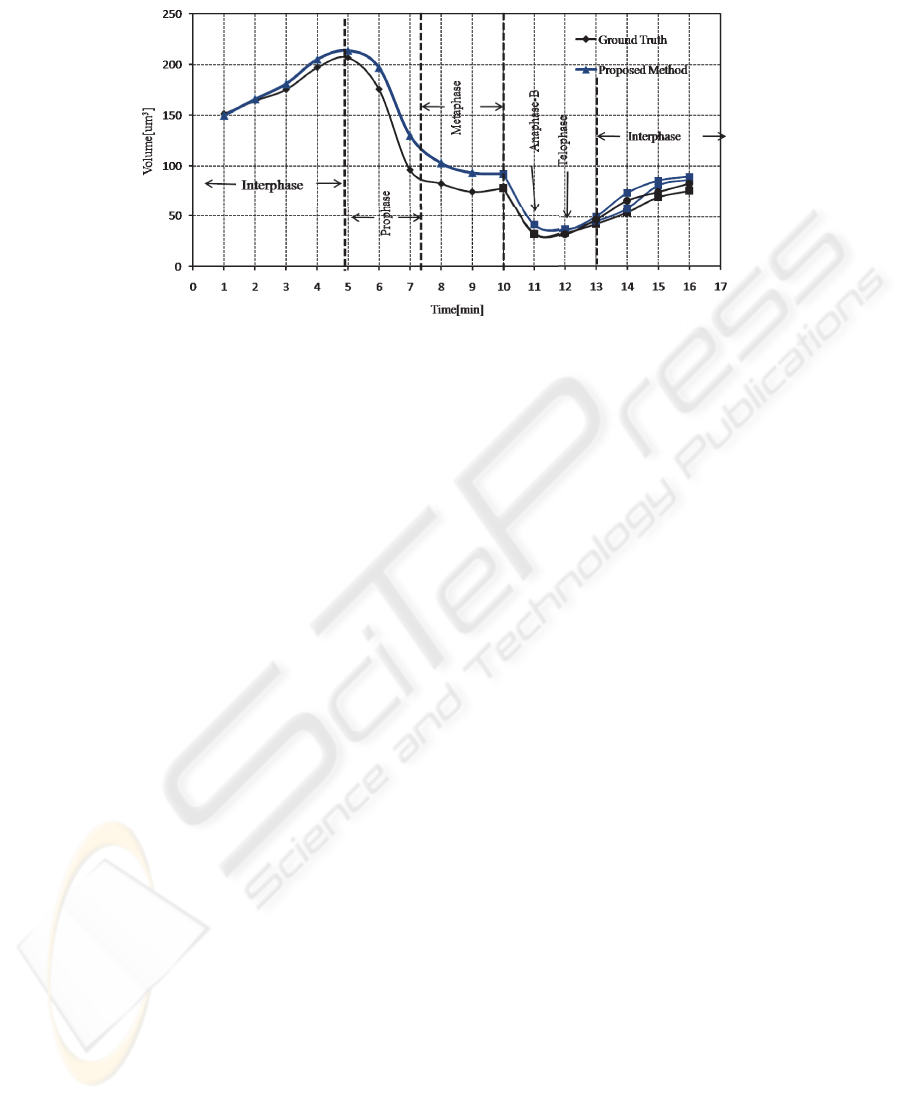
Fig.5. Cell cycle dependant changes of nuclear and chromosomal volume from interphase to the
end of anaphase in wildtype syncytium.
4 Conclusions
We presented a novel method for the detection of fluorescently labeled cell nuclei in
3D image stacks. Reliable segmentation of cell nuclei and mitotic chromosomes is very
important for the study of cell cycle progression in Live Drosophila Embryo. We intro-
duced a methodology based on narrow band level sets for isolating the cell nuclei from
background. The proposed method has been evaluated regarding object level and pixel
level accuracy. Preliminary results show that the outputs of the image segmentation are
suitable for downstream tracking, quantification and classification of identified image
objects.
References
1. Garcia, K., Duncan, T., Su, T.: Analysis of the cell division cycle in drosophila. Methods 41
(2007) 198–205
2. Adiga, P.S.U., Chauduri, B.B.: An efficient method based on watershed and rule-based merg-
ing for segmentation of 3-D histo-pathological images. Pattern recognition 34 (2001) 1449–
1458
3. Li, G., Umesh Adiga, Olson, K., John, F., Guzowshi, Barns, C.A., R. Badrinath: A hybrid
3D watershed algorithm incorporating gradient cues and object models for automatic seg-
mentation of nuclei in confocal image stacks. Cytometry A 56A (2003) 23–36
4. Gang Li, Chawala, M., Olson, K., Guzowski, J., Barnes, C., R. Badrinath: Hierarchical,
model-based merging multiple fragments for improved three-dimensional segmentation of
nuclei. Cytometry A 63A (2005) 20–23
5. Gang Li, Tianming Liu, Ashley T., Jingxin Nie, Guo, L., Mara, A., Holley, S., Stephen T C
Wang: 3D cell nuclei segmentation based on gradient flow tracking. BMC Cell Biology 8
(2007)
50

6. Dufour A., Shinin V., Tajbaksh S., Guillen N., Olivo-Marin J., Zimmer C.: Segmenting and
tracking fluorescent cells in dynamic 3D microscopy with coupled active surfaces. IEEE
Transactions on Image Processing 14 (2005)
7. A, D., JooHyun Lee, Nicole Vincent, Grailhe, R., Auguste Genovesio: 3D automated nu-
clear morphometric analysis using active meshes. In: Pattern recognition in Bioinformatics.
Volume LNBI4774. (2007) 356–367
8. Clarkson, M., R., S.: A His2AvDGFP fusion gene complements a lethal His2AvD mutant
allele and provides an in vivo marker for drosophila chromosome behavior. DNA and Cell
Biology (1999)
9. Silvia Cermelli, Yi Guo, Steven P., Gross, Michael A. W.: The lipid-droplet proteome reveals
that droplets are a protein-storage depot. Current Biology 16 (2006) 1783–1795
10. Wang, D.: A multiscale gradient algorithm for image segmentation using watershed. Pattern
Recognition 30 (1997) 2043–2052
11. Rambabu, C., Chakrabarti, I.: An efficient hillclimbing-based watershed algorithm and its
prototype architecture. Journal of signal processing systems 52 (2008) 281–295
12. L., C.D.: Computing minimal surfaces via level curvature flow. Journal of Computational
Physics 106 (1993) 77–91
13. Paragios N, Deriche R: Geodesic active contours and level sets for the detection and tracking
of moving objects. IEEE Trans. On PAMI 22 (2000) 266–280
14. H. -S. Wu, Barba J., Gil J.: Iterative thresholding for segmentation of cells from noisy
images. Journal of microscopy 197 (2000) 296–304
51
