A Cost Efﬁcient Approach for Automatic Non-Rigid

Registration of Medical Images

Sami Dhahbi, Walid Barhoumi and Ezzeddine Zagrouba

Equipe de Recherche en Syst`emes Intelligents en Imagerie et Vision Artiﬁcielle (SIIVA-ISI)

Institut Sup´erieur d’Informatique, 2 Rue Abou Rayhane Bayrouni, 2080 Ariana, Tunisia

Abstract. A common approach for non-rigid medical image registration is the

hierarchical image subdivision-based strategy. In this approach, images are pro-

gressively subdivided, locally registered, and elastically interpolated. Although

this approach seems to be among the fastest approaches for non-rigid registra-

tion, computation time is still a real challenge. This work deals with this prob-

lem and proposes a new hierarchical strategy. To reduce computational com-

plexity, we propose to combine in the same framework the hierarchical image

subdivision-based strategy with a Gaussian pyramid. The hierarchical subdivi-

sion method ensures that the registration process deals with small and large de-

formations, whereas the use of Gaussian pyramid decreases the computation time

enormously. The proposed framework is preliminary validated in the context of

monomodal registration by matching breast mammograms and MRI brain images

with simulated deformations. Registration quality is evaluated by using image

differences, mean square error, peak signal to noise ratio and correlation coef-

ﬁcient. Complexity study and experimental results show that the proposed ap-

proach reduces considerably the computation cost meanwhile maintaining com-

parable accuracy.

1 Introduction

Over the last years, advances in wide range of medical imaging modalities have led to

an increased need for sophisticated registration techniques, allowing clinicians to ad-

vantageously gain the maximum amount of complementary information from various

images. Indeed, image registration has widely opened up new medical imaging applica-

tions [5], such as serial MRI, perfusion imaging and image guided surgery and therapy

(IGT). Thus, proper integration of complementary information from two or more im-

ages acquired from different scanners, at different viewpoints, from different subjects

or at different time intervals is often desired. This process, called image registration or

alignment, can be done manually. However, manual registration is boring and very time

consuming. It is therefore desirable to establish fully automated registration. Its pur-

pose is to ﬁnd a geometrical transformation that relates the points of an image I to their

corresponding points of another image

I. During the past decades, many medical image

Dhahbi S., Barhoumi W. and Zagrouba E. (2009).

A Cost Efﬁcient Approach for Automatic Non-Rigid Registration of Medical Images.

In Proceedings of the 1st International Workshop on Medical Image Analysis and Description for Diagnosis Systems, pages 3-12

DOI: 10.5220/0001813800030012

 SciTePress

registration algorithms have been developed, and several survey papers have been pub-

lished [15,10, 8]. These methods may be classiﬁed according to the used information,

the similarity measure, the transformation model and the optimization process.

With respect to the ﬁrst criterion, the proposed methods are classiﬁed as feature-

based or area-based methods. The ﬁrst group is based on the extraction of salient struc-

tures in the image, whereas the latter operates directly on the image intensities, without

prior data reduction by the user or by a segmentation process. Since the ﬁnal registration

result of feature-based methods depends enormously on the segmentation step, its use

is recommended only if the images contain enough distinctive and easily detectable ob-

jects [10]. Thus, as medical images do not contain enough details, area-based methods

are rather employed. Nevertheless, the main drawback of these methods is the compu-

tation time.

The similarity criterion quantiﬁes the similarity between the images to be aligned.

Measures based on information theory, such mutual information (MI), are more suitable

for multiomodal registration and therefore they are often used in this case. Nevertheless,

several problems have to be faced when using MI, particularly if it is applied to small-

sized images, mainly computation coast and interpolation artefact [1]. Therefore, faster

but reliable criteria are rather employed in the case of monomodal registation. In par-

ticular, the correlation coefﬁcient (CC) is optimal when assuming a linear dependency

between images intensities, which is a reasonable hypothesis in case of mono-modal

registration [13].

The transformation model deﬁnes how one image can be deformed to match an-

other image. The simplest examples are the rigid and the afﬁne transformations. How-

ever, when the objects under investigation are highly non-rigidly deformed, a non-rigid

transformation, capable to deal with more localized spatial changes, is always needed

[4]. The most accurate non-rigid registration methods are based on physical models.

However, those methods are computationally very expensive. Therefore, various sim-

pliﬁcations have been proposed to approximate the underlying physical deformation

[5]. One possible way to approach the related problems is to model the elastic trans-

formation as an interpolation of multiple local rigid-body registrations. This approach

involves subdivision of one or both the participating images, followed by independent

registration of corresponding subimages. A smoothly global non-linear transformation

is then generated from the local registration solutions using interpolation schemes [9].

Nevertheless, non-rigid transformations are always deﬁned by a large number of param-

eters. Thus, searching for a such global registration transformation by using a similarity

measure may result on an abundance of local minima and an increasing computational

time. To overcome these problems, hierarchical matching strategies are always advised.

Initial matches are often performed rapidly due to a reduction in input data quantity or

the calculation of a simpliﬁed transformation. According to the reduction or the simpli-

ﬁcation done in the coarsest levels, hierarchical registration approaches can be classiﬁed

as hierarchies of data or warp complexity [8]. Hierarchies of data complexity require

parallel generation of a set of modiﬁed copies of the input images which contain de-

creasing levels of details. This will ideally create a hierarchy of images from the most

global to the most intricate. Such hierarchies of decreasing data complexity are pro-

vided by scale spaces, where the image size is constant in all levels, or by pyramids,

where image size is reduced in each successive level. In the latter case, the reduction in

the amount of data to be processed in the coarse level images may speed up the com-

putation of optimal parameters. This represents an additional advantage for pixel-based

matching schemes. On the other hand, registration warps can be summarized either by

coefﬁcients of basis functions or by displacements of landmarks. At each level of the

hierarchy, increasing the number of coefﬁcients in the former and the number of land-

marks in the latter, increases the complexity with which the warp can be described.

To be integrated in a computer-aided detection and diagnosis system, the non-rigid

registration method must be fast and automated. Consequently, a convenient choice of

the different components of the registration method may be as follows:

1. Used information: to be automated, the method must be area-based;

2. Similarity criterion: cross correlation can be used since we handle monomodal reg-

istration in our experiments;

3. Transformation model: as medical organs are elastic bodies, a robust elastic de-

formation model must be used. To decrease the computation cost, an appropriate

choice may be the one based on image-subdivision;

4. Optimization process: to accelerate the registration algorithm, hierarchical match-

ing strategies are very useful.

In this work, we propose a simple, but efﬁcient, modiﬁcation of the hierarchical im-

age subdivision-based strategy for non-rigid registration [9], which decreases its com-

putation cost. In fact, we combine in the same framework the hierarchical approach

with a Gaussian pyramid. The hierarchical image subdivision method ensures that the

registration process deals with small and large deformations, whereas the use of Gaus-

sian pyramid accelerates the registration process enormously. The rest of this paper is

organized as follows. The hierarchical subdivision strategy, the Gaussian pyramid and

related works which tend to combine hierarchies of data and warp are discussed in the

next section. The proposed framework and its validation are presented successively in

sections 3 and 4. Conclusions and ideas for future works are summarized in section 5.

2 Hierarchical Registration

2.1 Hierarchical Image Subdivision

Likar and Pernus [9] have developed a hierarchical framework for automated non-rigid

registration, with increasing warp complexity while increasing the numberof landmarks

in each level. The images to be registered are subdivided into four subimages, which

are then locally and independently registered by a rigid transformation. This process

is repeated until the regions are of a predetermined minimum size (Fig. 1). Thus, after

completing l stages, the image is divided into 4

equal-sized pieces. For each subim-

age, a rotation angle and a translation value are determined. Elastic thin-plate splines

technique [3] is then used to interpolate the centers of the registered sub-images. This

hierarchical approach ensures that the registration process deals both with small and

large deformations. Although this approach is faster than non-rigid algorithms based on

physical models and it seems to be among the fastest elastic registration approaches [7],

computation cost is the most challenging obstacle to widespread its incorporation into

real time clinical applications.

Fig.1. The classical hierarchical image-based subdivision approach [9] and the Gaussian pyra-

midal approach for elastic image registration.

2.2 Gaussian Pyramid

Multiresolution is usually desirable in image registration, since it saves time and also

improves the registration accuracy [11]. Gaussian pyramid is the most commonly used

multiresolution representation for image registration [14]. It requires the parallel gen-

eration of a family of images from each of the original source and target images, where

image size (resolution) is reduced in each successive level. Each level is formed by ﬁrst

applying Gaussian smoothing (on the original images) with increasing scale and then

downsampling the previous level (smoothed images) (Fig. 1.). In addition to avoiding

local minima traps, the Gaussian pyramid has the advantage of reducing computation

time since the quantity of data is less in the lowest levels [8].

2.3 Combining Hierarchies of Data and Warp

In order to decrease computation cost of non-rigid registration, some works tend to

combine hierarchies of data and warp complexity on the same framework. For example,

Hellier et al. [5] proposed a hierarchical multiresolution and multigrid framework for

non-rigid registration of MR images of the head. At each level of resolution, a multigrid

minimization based on successive partitions of the initial volume is used. This method

is based on transformations of higher complexity at initial subdivision levels with larger

subvolumesand simpler modes at later levels having smaller subvolumes. Besides, Auer

et al. [2] proposed an automatic non-rigid registration scheme for stained histological

sections. They developed a hierarchical registration algorithm, by basically using a fast

coarse rigid registration step, followed by a slower, but ﬁner, non-rigid elastic registra-

tion. For the coarse registration, they used an image pyramid to speed up the algorithm.

Although those methods combine hierarchy of data and warp, only either the data or

the warp complexity increases at each level of the hierarchy.

Fig.2. The proposed hierarchical framework for non-rigid image registration.

3 Proposed Framework

The proposed method combines the hierarchical image subdivision-based approach and

Gaussian image pyramid. Contrary to the aforementioned methods, the complexity of

both data and warp increase at each level of the hierarchy (Fig. 2.).

Firstly, we construct Gaussian image pyramids for the reference and the target im-

ages. At each level of the pyramid, the images to be registered are subdivided into

subimages of predetermined minimum size, which are then locally registered. In the

coarsest level, as the image size is equal to the minimum size, only global rigid regis-

tration is required. In the second level, the images are subdivided into four subimages,

which are then locally and independently registered by a rigid transformation. This

process is repeated until the ﬁnest level in the pyramid is reached. As the algorithm

progresses to ﬁner resolutions, both the size of the image and the number of landmarks

increase. In local rigid registration, we use CC (1) as a similarity measure since we han-

dle monomodal registration. In addition, Powell’s multidimensional scheme [6] is used

as optimization method. Note that the levels’ number is imposed by the predetermined

minimum size of the smaller used subimage.

CC =

(I(i, j) − I)(

I(i, j) −

(

(I(i, j) − I)

)(

(

I(i, j) −

)

. (1)

Finally, thin-plate splines (TPS) is used to elastically interpolate the local transfor-

mations to obtain the ﬁnal global smooth transformation. Indeed, TPS is a common

tool for multi-dimensional interpolation problems and has useful smoothing properties.

The use of this technique for elastic registration is pioneered by Bookstein [3]. The

method has an elegant algebra expressing the approximation of a physical bending of a

thin metal plate on point constraints. The smooth function f (x, y), describing the plate,

minimizes the following bending energy function:

Z Z

(

∂

∂x

)

+ 2(

∂

∂x∂y

)

+ (

∂

∂y

)

dxdy. (2)

Suppose that we have two sets of n corresponding centers (x

, y

) and (`x

, `y

) of the

registered subimages, and let f

and f

two separate thin-plate spline functions which

model the displacement of the subimages centers (landmarks) respectively in the x

and y direction ((f

, y

), f

, y

)) = (`x

, `y

)). The thin-plate spline interpolation

functions which maps corresponding points can be written as:

(x, y) = a

+ a

x + a

y +

i=1

U(|(x, y) − (x

, y

)|), (3)

(x, y) = a

+ a

x + a

y +

i=1

U(|(x, y) − (x

, y

)|). (4)

where U (r) = r

log(r

) is fundamental solution of the biharmonic equation (∆

U =

0) that satisﬁes the condition of bending energy minimization. The parameters a

, a

and a

represent the linear afﬁne transformation, while w

and w

represent the weights of the non-linear radial interpolation function U.

4 Validation

4.1 Computational Complexity

To illustrate the usefulness and the gain obtained in computation cost by our approach,

we compare its computation complexity with the one of the classical hierarchical subdi-

vision based scheme. In fact, the cpu time of a registration process is mainly consumed

during the computation of the similarity measure. Therefore, our analysis of computa-

tional complexity will concentrate on the estimation of CC. According to the equation

(1), the computation of the numerator in the CC formula requires T

multiplications

when the subimages’ size is T × T . In addition, to simplify the complexity computa-

tion, we assume that local rigid transformations are composed only of translations over

x and y axis, and the allowable translation in each direction must not exceed the quarter

of the image size. If an exhaustive search is used to ﬁnd parameters of local transfor-

mations, then the complexity of computing CC in local registration is

. Thus, given

two input N × N images I (reference) and

I (target) and let the number of levels is l

(the smallest subimage size is then

l−1

), in each level j (1 ≤ j ≤ l) the number of

subimages to be rigidly registered is 4

j−1

for the proposed approach as well as for the

classical one. However, the size of each subimage is

l−1

(resp.

j−1

) in the case of our

(resp. classical) solution. Thus, the cost of the level j is N

(2j−4l)

(resp. N

(−2j)

)

in our (resp. the classical) case. Consequently, the total cost of the suggested scheme

(5) and the one of the classical hierarchical scheme (6) are consecutively deﬁned by:

j=1

(2j−4l)

4.N

−l

(5)

j=1

(−2j)

4.N

− 1) (6)

Besides, we compared the total cpu time for the two studied schemes while specify-

ing the evolution of this time from a level of the hierarchy to the next one (Fig. 3). This

was done for 512 × 512 MRI images with l = 4. Methods are implemented in Matlab,

and the platform used is a Windows PC with Intel P-4 1.6 GHz processor and 1G RAM

memory. While comparing the complexity cost as well as the total cpu time of the pro-

posed solution with those of the classical subdivision-based scheme, it is clear that our

method outperforms considerably the classical approach in terms of computation cost.

1 2 3 4

500

1000

1500

2000

2500

3000

3500

Level

Computation time (s)

Classical Approach

Proposed Approach

Fig.3. Evolution of the cpu time relatively to the hierarchy level.

4.2 Registration Accuracy

In order to validate the registration accuracy of the proposed framework, simulated

deformation are randomly introduced to breast mammograms (from the MIAS digital

mammogram database [12]) and to MRI brain images. Since we handle images of the

same modality, image-subtraction comparison can be used to visually assess the quality

of the registration process (Fig. 4, Fig. 5). Besides, to quantitatively assess the quality of

the registration, we compute the correlation coefﬁcient (CC) (1), the mean square error

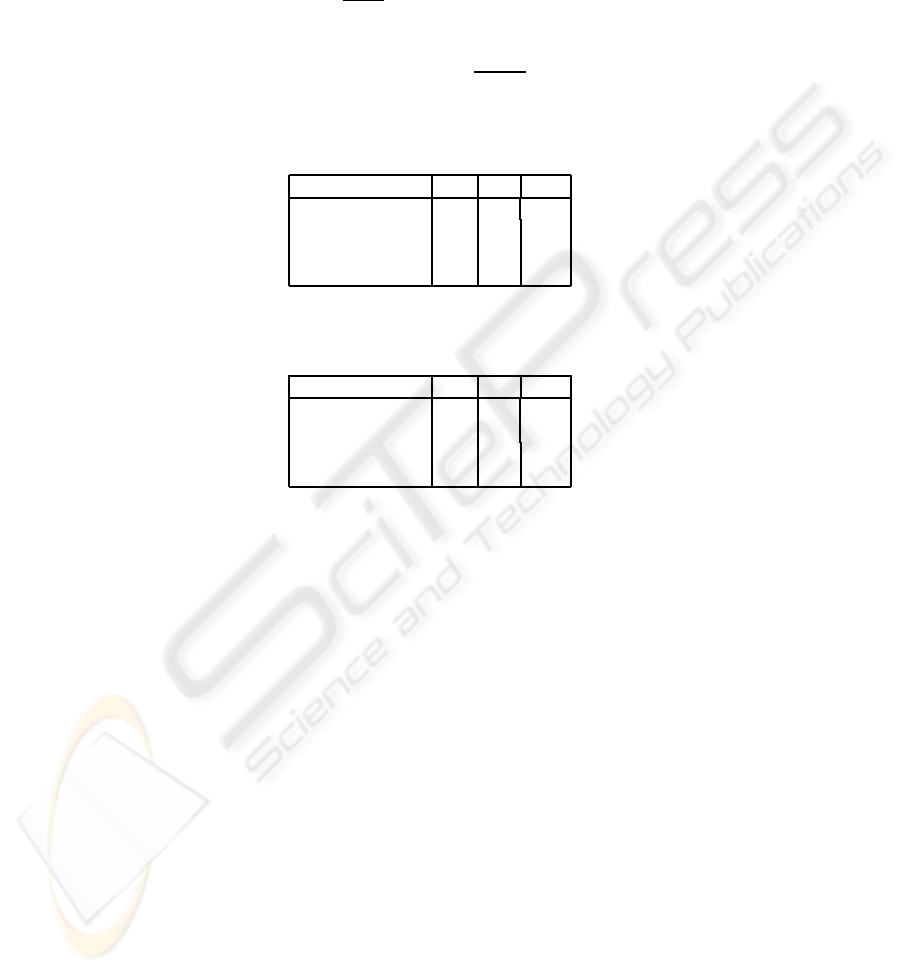
(MSE) (7) and the peak signal to noise ratio (PSNR) (8). In Tab.1 (resp. Tab.2) we illus-

trate the CC, MSE and PSNR errors for the pre-registration, the afﬁne registration, the

classical hierarchical subdivision approach and the proposed framework recorded with

mammogram (resp. MRI brain) images. The above obtained results indicate that both

the classical hierarchical subdivision approach and the proposed framework perform

better than afﬁne registration. Moreover, we can deduce that the classical and the pro-

posed approaches produce almost similar results in terms of CC, MSE and PSNR. This

proves the effectiveness of the proposed framework, since it accelerates the registration

process without signiﬁcant loss of the registration quality. Note that afﬁne registration

removes most of the global differences from the studied images, whereas non-rigid reg-

istration performs mainly local improvements.

MSE =

[I(i, j) −

I(i, j)]

. (7)

P SNR = 10.log

255

MSE

. (8)

Table 1. CC, MSE and PSNR registration errors for mammograms.

CC MSE PSNR

Pre-registration 0.79 2729 31.70

Afﬁne registration 0.951 661 45.87

Classical approach 0.953 636 46.27

Proposed approach 0.953 635 46.28

Table 2. CC, MSE and PSNR registration errors for brain MRI.

CC MSE PSNR

Pre-registration 0.64 3423 29.44

Afﬁne registration 0.89 1116 40.64

Classical approach 0.916 847 43.39

Proposed approach 0.911 897 42.82

5 Conclusions

Although the hierarchical image subdivision-based procedure seems to be among the

fastest non-rigid registration methods, its computation cost is a real challenge to be in-

tegrated in real-time clinical routines. To reduce the computational complexity, we have

proposed a simple and elegant method which combine in the same framework the hier-

archical method with a Gaussian pyramid. Indeed, a Gaussian pyramid is ﬁrst deﬁned

for each of the reference and the target images. Then, at each level of the pyramid, the

images to be registered are subdivided into four quarters, which are then locally and

independently registered using a rigid transformation based on CC score and Powell

optimization technique. Then, relatively to each subimage, a landmark is deﬁned as its

center. Lastly, given the set of corresponding landmarks, the TPS interpolator is used to

estimate the correspondencefunction between the two studied images. Experimental re-

sults show the effectiveness of our method for non-rigid registration of medical images.

One of the beneﬁts of the proposed approach is its ability to run automatically, avoid-

ing the reliance on accurate segmentation or control-point extraction. Another beneﬁt

is the reduction in computation complexity. Indeed, when compared to classical ap-

proach, our solution decreases considerably computation cost without meaningful loss

Fig.4. Hierarchical registration results of mdb050 mammogram with simulated deformations:

a) Target mammogram. b) Reference mammogram. c) Afﬁne registered image. Non-rigid regis-

tered image using: d) Classical hierarchical non-rigid registration, e) Proposed method. f) Pre-

registration difference image. Post-registration difference image using: g) Afﬁne registration, h)

Classical hierarchical non-rigid registration, i) Proposed method.

Fig.5. Hierarchical registration results of brain MRI with simulated deformations: a) Target im-

age. b) Reference image. c) Afﬁne registered image. Non-rigid registered image using: d) Classi-

cal hierarchical non-rigid registration, e) Proposed method. f) Pre-registration difference image.

Post-registration difference image using: g) Afﬁne registration, h) Classical hierarchical non-rigid

registration, i) Proposed method.

of the registration accuracy. Actually, we are working on the application of the sug-

gested approach for bilateral mammogram registration in the context of breast tumors

diagnosis. Besides, since the proposed method deals with intensity based registration,

it is of great interest to extend this approach to multimodal registration. Therefore, our

future work will focus in the adaption of the proposed framework to mutual information

based registration. Finally, as the partitioning scheme ignores the information, notably

edges information, which lies exactly on the partition, it seems interesting that each

subimage can overlaps with its adjacent subimages.

References

1. Andronache, A., Von Siebenthal, M. Szekely, G. Cattin, P.: Non-rigid Registration of Multi-

modal Images using Both Mutual Information and Cross-correlation. Medical Image Analy-

sis. (2007) 1–13

2. Auer, M., Regitnig, P., Holzapfel, G.A.: An Automatic Nonrigid Registration for Stained

Histological Sections. IEEE Trans. on Image Processing. Vol. 14(4). (2005) 475–486

3. Bookstein, F.L.: Principal Warps: Thin-Plate Splines and the Decomposition of Deforma-

tions. IEEE Trans. Pattern. Anal. Math. Intell. Vol. 11. (1989) 567–585

4. Crum, W.R., Hartkens, T., Hill, D.L.G.: Non-Rigid Image Registration: Theory and Practice.

The British Journal of Radiology. Vol. 77. (2004) 140–153

5. Hellier,P., Barillot, C., Memin, E., Perez, P.: Hierarchical Estimation of a Dense Deformation

Field for 3-D Robust Registration. IEEE Trans. on Medical Imaging, Vol. 20(5). (2001) 388–

402

6. Jenkinson, M., Smith, S.: A Global Optimisation Method for Robust Afﬁne Registration of

Brain Images. Medical Image Analysis, Vol. 5. (2001) 143–156

7. Krucker, J.F., LeCarpentier, G.L., Fowlkes, J.B., Carson, P.L.: Rapid Elastic Image Registra-

tion for 3-D Ultrasound. IEEE Trans. on Medical Imaging. Vol. 21. (2002) 1384–1394

8. Lester, H., Arridge, S.R.: A Survey of Hierarchical Non-Linear Medical Image Registration.

Pattern Recognition. Vol. 32. (1999) 129–149

9. Likar, B., Pernus, F.: A Hierarchical Approach to Elastic Registration Based on Mutual In-

formation. Image and Vision Computing. Vol. 19. (2001) 33–44

10. Maintz, J.B.A., Viergever, M.A.: A survey of Medical Image Registration. Medical Image

Analysis, Vol. 2. (1998) 1–36

11. Pluim, J.W., Maintz, J.A., Viergever, M.A.: Mutual Information Based Registration of Med-

ical Images: A survey, IEEE Transactions on Medical Imaging, Vol. 22(8). (2003) 986–1004

12. Suckling, J., Parker, J., Dance, D.R.: The Mammographic Image Analysis Society Digital

Mammogram Database. Proceedings of the International Workshop on Digital Mammog-

raphy, Vol. 1069 of Exerpta Medica, International Congress Series, York-England. (1994)

375–378

13. Wiest-Daessle, N., Yger, P., Prima, S., Barillot, C.: Evaluation of a New Optimisation Algo-

rithm for Rigid Registration of MRI Data. Progress in Biomedical Optics and Imaging. Vol.

8(1) (2007

14. Wu, J., Chung, A.S: Multimodal Brain Image Registration Based on Wavelet Transform

Using SAD and MI. MIAR 2004, LNCS 3150. (2004) 270–277

15. Zitova, B., Flusser, J.: Image Registration Methods: A Survey. Image and Vision Computing.

Vol. 11. (2003) 977–1000